Games101学习笔记 - 基础数学
向量
向量:方向和长度,没有起始位置
向量长度:各个方向平方相加开方
单位向量:向量除向量的长度
点乘
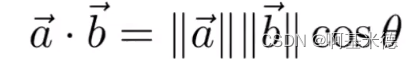
在笛卡尔坐标系中的点乘计算:
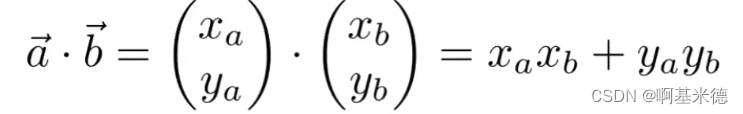
几何意思:
表示一个向量在另一个向量上的投影
点乘在图形学中应用:
1.得到两个向量的夹角2.求一个向量在另一个向量上的投影3.确定两个向量接进度(角度越小越接近)
叉乘
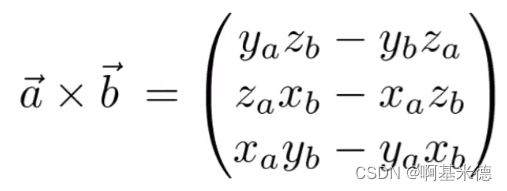
|AxB| = |A| |B| sinの
性质
叉乘顺序不同得到的结果也不同叉乘的结果和两个原始向量都垂直向量叉乘自己得到0向量
几何意思:
向量叉乘的结果是一个垂直于两个原始向量的向量。
右手螺旋定则判断叉乘方向:
这个方向可以使用右手螺旋定律判断(默认是右手坐标系内)。比如向量A叉乘向量B,把向量A,B移动到同起点(因为向量平移表示的还是原向量)。 四指并拢,大拇指伸直,四指指向A向量然后围绕手掌四指旋转到B方向,此时大拇指就是AB叉乘的向量的方向。
点乘在图形学中应用:
1.叉乘可以判断一个向量在另一个向量的左右解释:根据上述右手螺旋定则我们可以法线A叉乘B,和B叉乘A的得到的方向是不同的,所以提我们可以根据此来判断该A在B的左右。
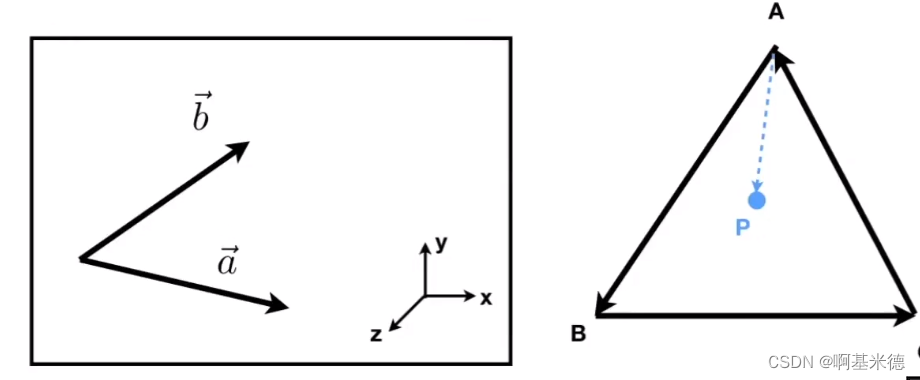
2.判断点在三角形内解释:因为我们已经知道了叉乘可以判断一个向量在另一个向量的左右关系。如下图,当AP在AB右侧,BP在BC右侧,CP在CA右侧。那么我们可以断定P被ABC包围,就是P在ABC三角形内。
矩阵
矩阵就是一系列数字经过m行n列的形式排列的组合。
矩阵乘法
矩阵相乘的前提是(M x N)(N x P)第一个矩阵的列数 等于第二个矩阵的行数矩阵乘结果的(i,j)的结果是第一个矩阵的i行表示的向量和第二个矩阵j列表示的向量的点积结果
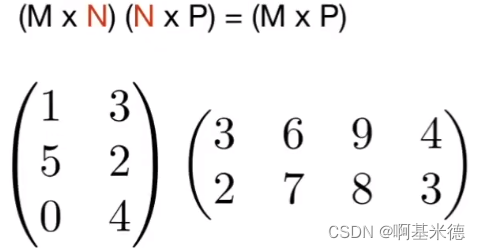
规律:
互逆矩阵乘得到单位矩阵,单位矩阵对角线为1,其他为0 矩阵乘没有交换律,有结合律和分配律矩阵和向量的乘法,认为矩阵和列矩阵乘
点乘写成矩阵的形式:
a和b的点乘是a的转置矩阵和b的列矩阵相乘
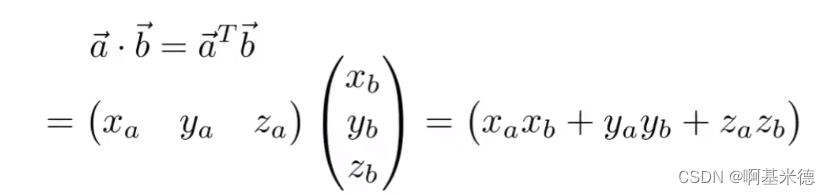
叉乘写成矩阵的形式:
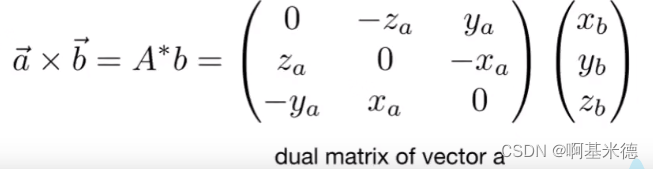
相关文章:
Games101学习笔记 - 基础数学
向量 向量:方向和长度,没有起始位置 向量长度:各个方向平方相加开方 单位向量:向量除向量的长度 点乘 在笛卡尔坐标系中的点乘计算: 几何意思: 表示一个向量在另一个向量上的投影点乘在图形学中应用&a…...

Linux进程的认识
查看进程指令proc/ps 注意哦, 我们经常使用的指令, 像ls, touch…这些指令在启动之后本质上也是进程 proc 是内存文件系统, 存放着当前系统的实时进程信息. 每一个进程在系统中, 都会存在一个唯一的标识符(pid -> process id), 就如同学生在学校里有一个专门的学号一样. 大…...
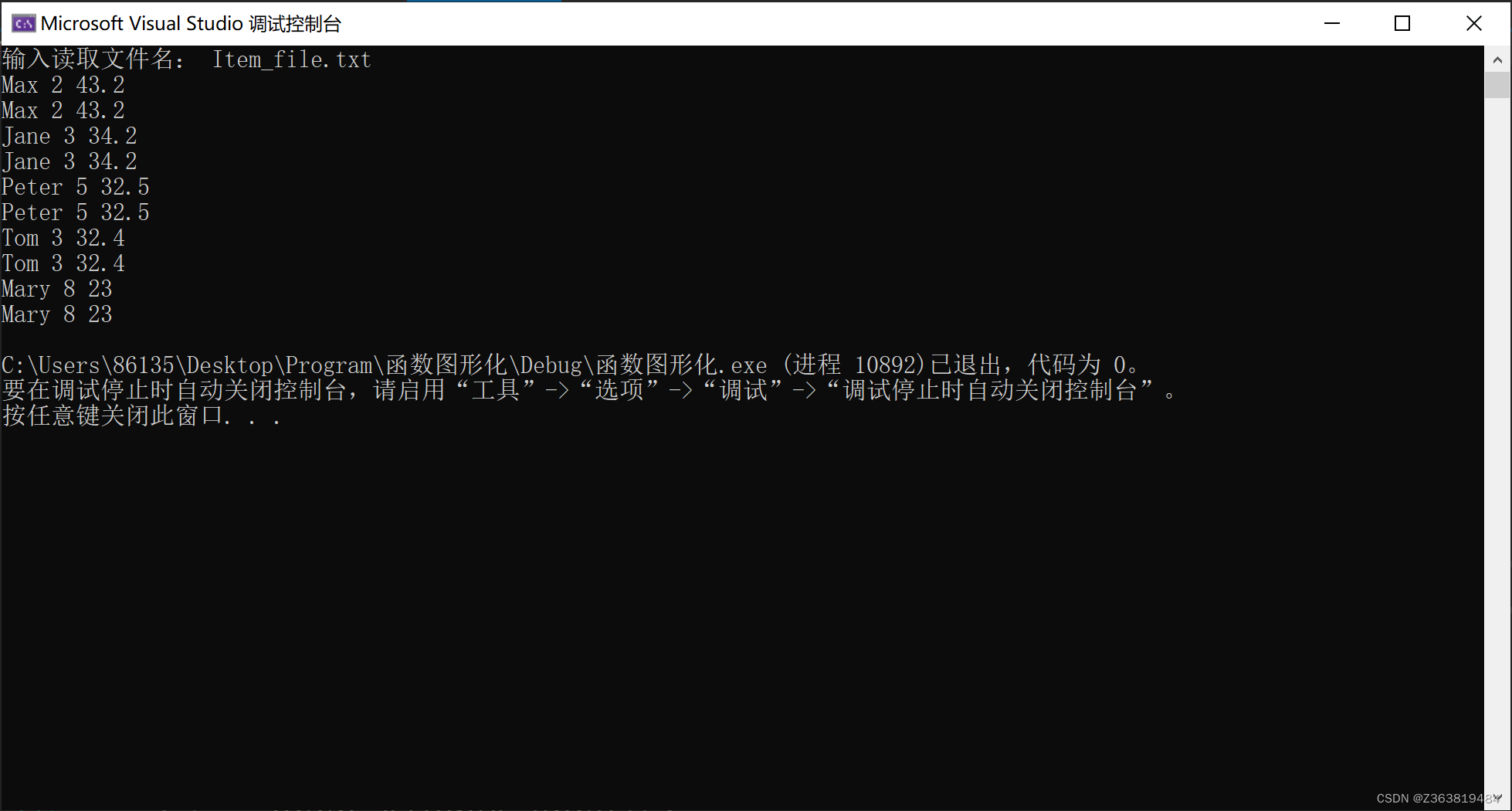
向量vector与sort()
运行代码: //向量与sort() #include"std_lib_facilities.h" //声明Item类 struct Item {string name;int iid;double value;friend istream& operator>>(istream& is, Item& ii);friend ostream& operator<<(ostream& o…...

Netty学习(三)
文章目录 三. Netty 进阶1. 粘包与半包1.1 粘包现象服务端代码客户端代码 1.2 半包现象服务端代码客户端代码 1.3 现象分析粘包半包缘由滑动窗口MSS 限制Nagle 算法 1.4 解决方案方法1,短链接方法2,固定长度方法3,固定分隔符方法4,…...

c++学习(布隆过滤器)[23]
布隆 布隆过滤器(Bloom Filter)是一种概率型数据结构,用于判断一个元素是否可能存在于一个集合中。它使用多个哈希函数和位图来表示集合中的元素。 布隆过滤器的基本原理如下: 初始化:创建一个长度为m的位图…...
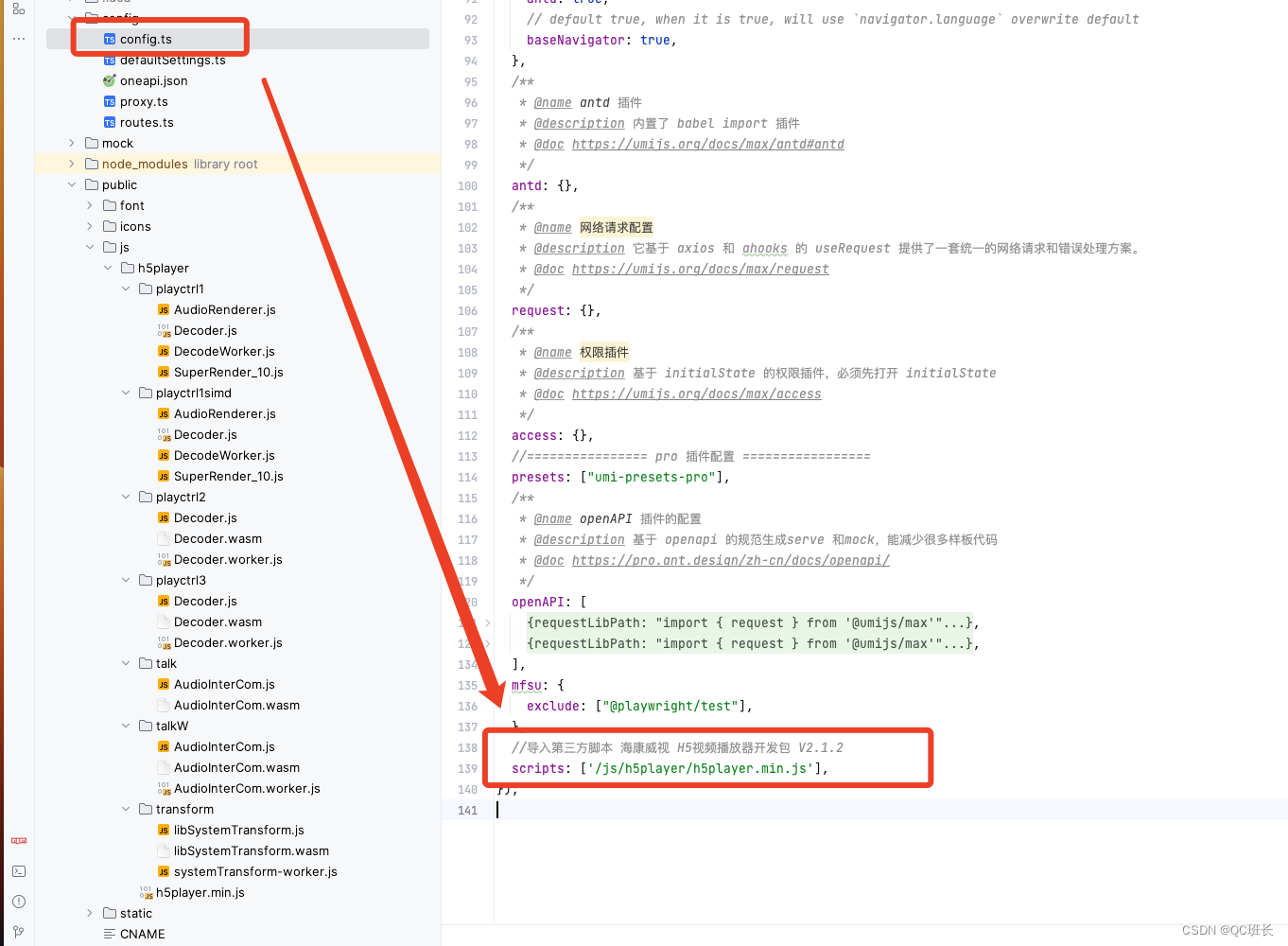
React的UmiJS搭建的项目集成海康威视h5player播放插件H5视频播放器开发包 V2.1.2
最近前端的一个项目,大屏需要摄像头播放,摄像头厂家是海康威视的,网上找了一圈都没有React集成的,特别是没有使用UmiJS搭脚手架搭建的,所以记录一下。 海康威视的开放平台的API地址,相关插件和文档都可以下…...
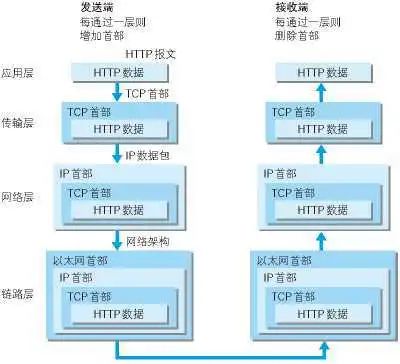
细讲TCP三次握手四次挥手(二)
TCP/IP 协议族 应用层 应用层( application-layer )的任务是通过应用进程间的交互来完成特定网络应用。应用层协议定义的是应用进程(进程:主机中正在运行的程序)间的通信和交互的规则。 对于不同的网络应用需要不同的应用层协议…...
)
LeetCode Top100 Liked 题单(序号19~)
19. Remove Nth Node From End of List 题意:给一个链表,删除从尾数起的第n个结点,返回头节点。 我的思路 指针到最后,数出来有多少个,之从前向后数,再删掉节点 代码 10ms Beats 16.06% class Solution…...
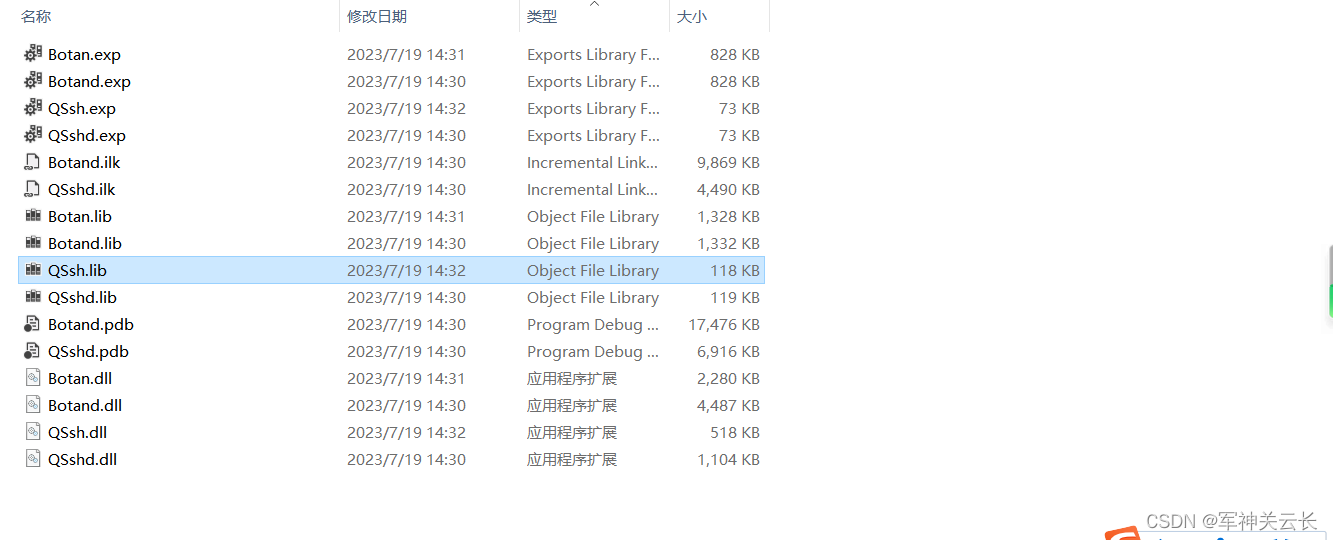
qssh使用
到官网下载qssh的源码QSsh-botan-1,使用qtcreator打开后,直接编译,即可得到qssh的库 头文件将QSsh-botan-1\src\libs\ssh目录下的.h文件拷到include文件夹下,即为库头文件。 qssh有个问题,如果你将qssh的类放在子线程…...

持续部署CICD
目录 (1)CICD的开展场景 (2)项目实际应用 CICD 是持续集成(Continuous Integration)和持续部署(Continuous Deployment)简称。指在研发过程中自动执行一系列脚本来降低开发引入 bug…...

ARM 循环阻塞延迟函数
串行驱动的关键是双方能够按照既定的时序进行检测、设置相关引脚上的电平,比如单总线、I2c这样基本的可以用GPIO模拟的时序协议,需要主从双方,必须在链路接口内严格按照微妙级的延迟单位进行时序同步。 所以,在这种对时间要求很敏…...

Spark的DataFrame和Schema详解和实战案例Demo
1、概念介绍 Spark是一个分布式计算框架,用于处理大规模数据处理任务。在Spark中,DataFrame是一种分布式的数据集合,类似于关系型数据库中的表格。DataFrame提供了一种更高级别的抽象,允许用户以声明式的方式处理数据,…...

WPF线程使用详解:提升应用性能和响应能力
在WPF应用程序开发中,线程的合理使用是保证应用性能和响应能力的关键。WPF提供了多种线程处理方式,包括UI线程、后台线程、Task/Async Await和BackgroundWorker。这些方式与传统的Thread类相比,更加适用于WPF框架,并能够简化线程操…...
ava版知识付费平台免费搭建 Spring Cloud+Spring Boot+Mybatis+uniapp+前后端分离实现知识付费平台
提供私有化部署,免费售后,专业技术指导,支持PC、APP、H5、小程序多终端同步,支持二次开发定制,源码交付。 Java版知识付费-轻松拥有知识付费平台 多种直播形式,全面满足直播场景需求 公开课、小班课、独…...

libuv库学习笔记-basics_of_libuv
Basics of libuv libuv强制使用异步和事件驱动的编程风格。它的核心工作是提供一个event-loop,还有基于I/O和其它事件通知的回调函数。libuv还提供了一些核心工具,例如定时器,非阻塞的网络支持,异步文件系统访问,子进…...
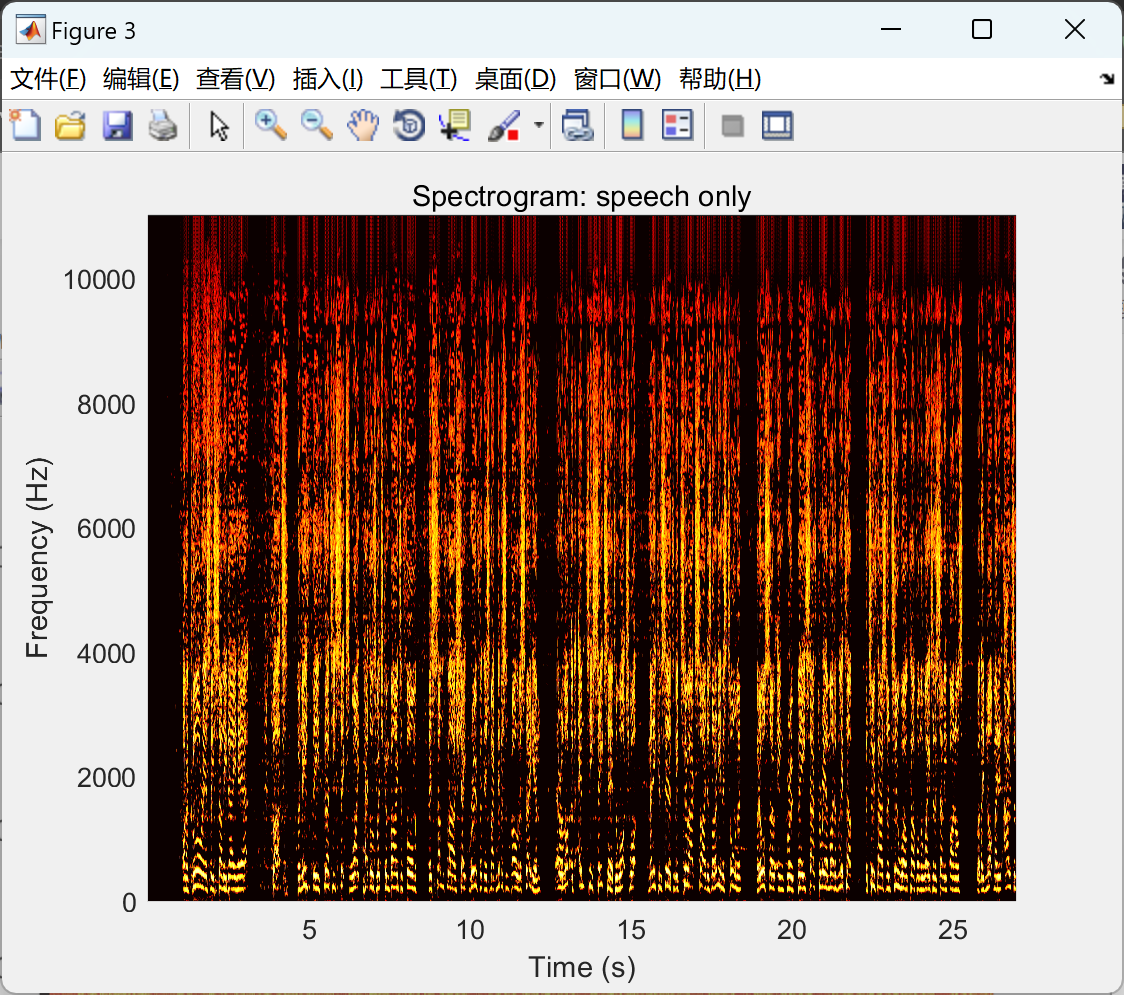
【Vuvuzela 声音去噪算法】基于流行的频谱减法技术的声音去噪算法研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
Vue + Element-ui组件上传图片报错问题解决方案
在前端开发中,我们经常需要模拟网络请求以进行单元测试或开发调试。而在模拟网络请求时,我们常常会使用到MockXMLHttpRequest对象。MockXMLHttpRequest对象是一个用于模拟XMLHttpRequest对象的工具,它提供了一种简单的方式来模拟网络请求&…...

java商城系统和php商城系统对比
java商城系统和php商城系统是两种常见的电子商务平台,它们都具有一定的优势和劣势。那么,java商城系统和php商城系统又有哪些差异呢? 一、开发难度 Java商城系统和PHP商城系统在开发难度方面存在一定的差异。Java商城系统需要使用Java语言进…...
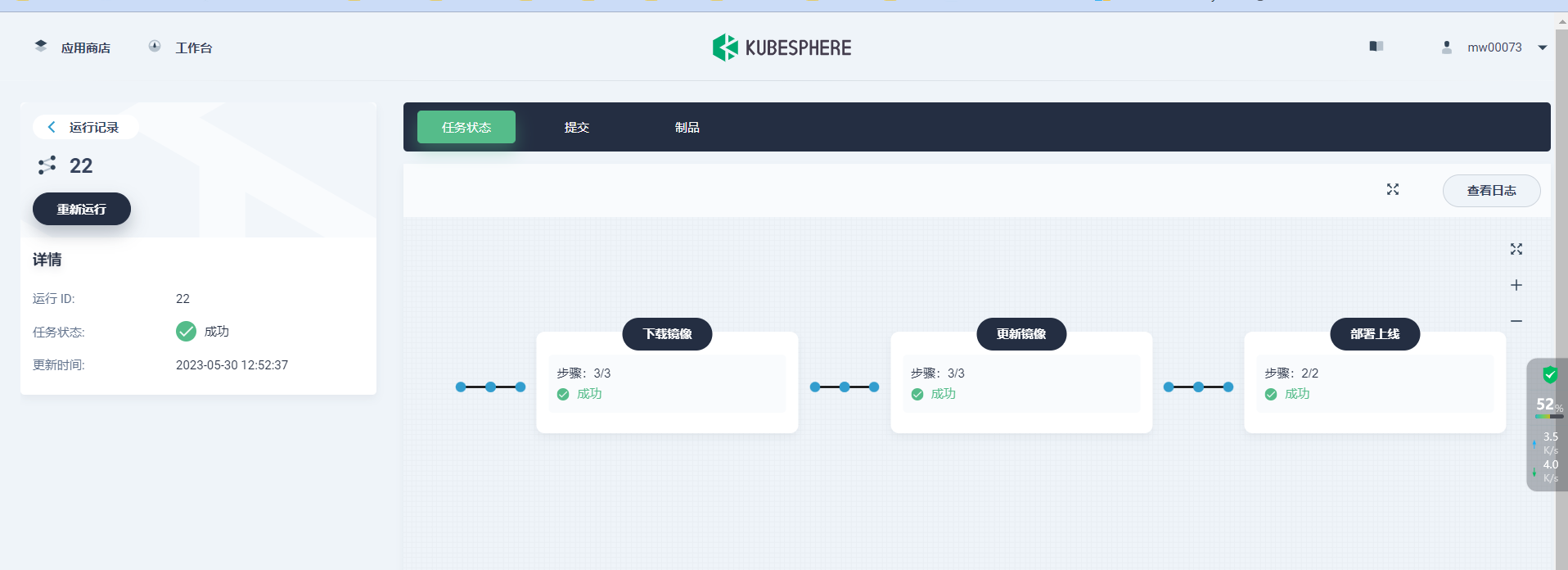
某制造企业基于 KubeSphere 的云原生实践
背景介绍 随着业务升级改造与软件产品专案的增多,常规的物理机和虚拟机方式逐渐暴露出一些问题: 大量服务部署在虚拟机上,资源预估和硬件浪费较大;大量服务部署在虚拟机上,部署时间和难度较大,自动化程度…...
Electron 学习_BrowserWindow
BrowserWindow创建并控制浏览器窗口(主进程) 条件:在 app 模块 emitted ready 事件之前,您不能使用此模块。 1.在加载页面时,渲染进程第一次完成绘制时,如果窗口还没有被显示,渲染进程会发出 ready-to-show 事件 。 在…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...
