垃圾回收标记阶段算法
1.标记阶段的目的
主要是在GC在前,判断出哪些是有用的对象,哪些是需要回收的对象,只有被标记为垃圾对象,GC才会对其进行垃圾回收。判断对象是否为垃圾对象的两种方式:引用计数算法和可达性分析算法。
2.引用计数算法(现在不再使用)
引用计数算法实现相对比较简单,就是给每一个对象保存一个引用计数器,记录此对象被引用的次数。只有该对象的引用次数为0,才表示该对象不在被使用,即可回收。
优点:便于实现,回收及时,判定效率高。
缺点:
-
因为要有引用计数器,所以需要额外的空间。
-
每次的操作都要个计数器重新赋值,所以需要额外的时间。
-
(重点)无法处理循环引用的问题,比如说外部P引用了A,而A引用了B,B又引用了C,C又引用了A,那么对于A,B,C其计数器为2,1,1,那么此时如果外部引用P赋值为null,及无外部引用了,但是A,B,C计数器依然为1,无法被回收,常此就会出现内存泄露。

3.可达性分析算法(也称为根搜索算法、追踪性垃圾收集)
可达性算法可以解决循环引用的问题,其思路为以根为起始点向下搜索,存活的对象就是与根直接或者间接相连的对象,所搜索经过的路径称为引用链,如果未被搜索到,则表明不可达,就标记为垃圾对象。
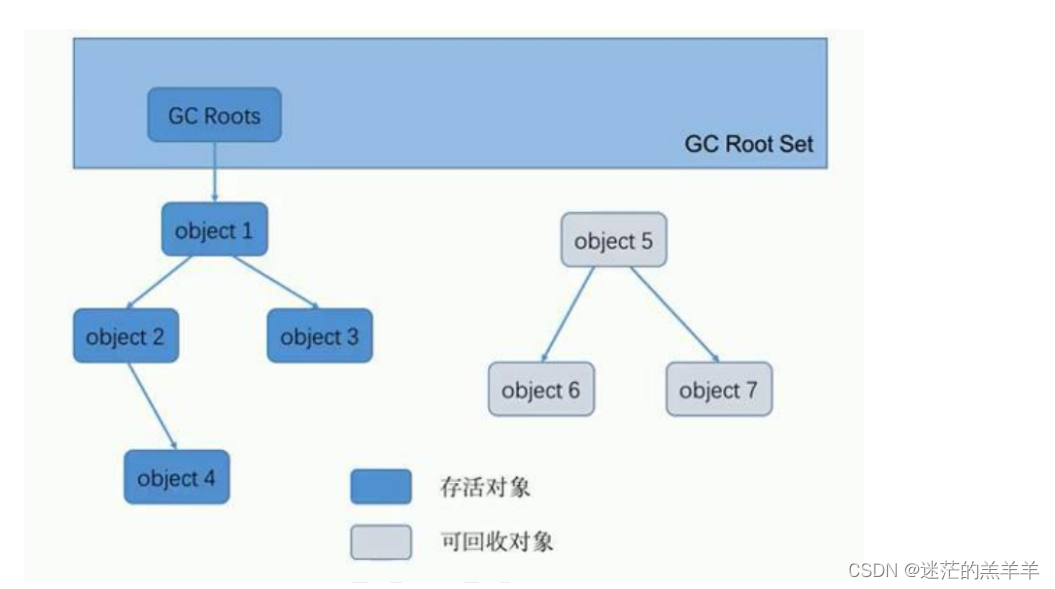
那么要作为根的判断标准是什么呢?
-
虚拟机栈中引用的对象(如局部变量...)。
-
方法区中类的静态变量。
-
被同步锁synchronized持有的对象。
-
Java虚拟机内部的使用。
4.对象的finalization机制
finalize()方法机制,是指对象被回收前由GC调用的方法,只会调用一次,Java提供了对象被销毁前允许开发人员来自定义销毁前要做的事情,finalize()方法是Object类中的方法,此方法内没有任何的实现,开发人员可以重写该方法。不要主动的去调用finalize()方法。因为:
-
finalize()方法可以使对象不在被销毁,在临死前拉一把。
-
如果不发生GC,finalize方法是没有执行机会的。
-
一个糟糕的finalize()可能会使程序崩溃,比如里面自定义一个死循环。
5.由于finalize(),对象的三种状态
-
可触及的,及可从根到达此对象。
-
可复活的,对象被标记为垃圾,但是可能在finalize()方法中被拯救。
-
不可触及的,对象的finalize()方法被调用了,并且没有复活。
具体的过程:一个对象要被回收,要经历两次标记的过程,如果此对象没有任何的引用,则会被标记为垃圾对象,等待回收,在回收前,执行该对象的finailze()方法,如果没有重写该方法,对象就会为不可触及状态被清理,如果重写了该方法,则会被加入到队列中,由一个Finalizer低优先级的线程来执行,如果在方法中没有补救,那么第二次标记就会标记该对象将会彻底被回收清理,如果在finalize()方法中对象又建立了联系,那么此对象又会进入可触及的状态,如果又没有了引用,finalize()方法不会在被调用(只会调用一次),对象直接会变为不可触及的状态。
相关文章:

垃圾回收标记阶段算法
1.标记阶段的目的 主要是在GC在前,判断出哪些是有用的对象,哪些是需要回收的对象,只有被标记为垃圾对象,GC才会对其进行垃圾回收。判断对象是否为垃圾对象的两种方式:引用计数算法和可达性分析算法。 2.引用计数算法…...

泰晓科技发布 Linux Lab v1.2 正式版
导读近日消息,Linux Lab 是一套用于 Linux 内核学习、开发和测试的即时实验室,官方称其“可以极速搭建和使用,功能强大,用法简单”。 自去年 12 月份发布 Linux Lab v1.1 后,v1.2 正式版目前已经发布于 GitHub 及 Gite…...

王道数据结构-代码实操1(全注解版)
#include<stdio.h>void loveyou(int n){ // 传入参数类型为int型,在此函数中表示为n;返回值类型为void,即没有返回值; int i1; //定义了一个整数型变量i,且只在loveyou函数中有用;while(i…...
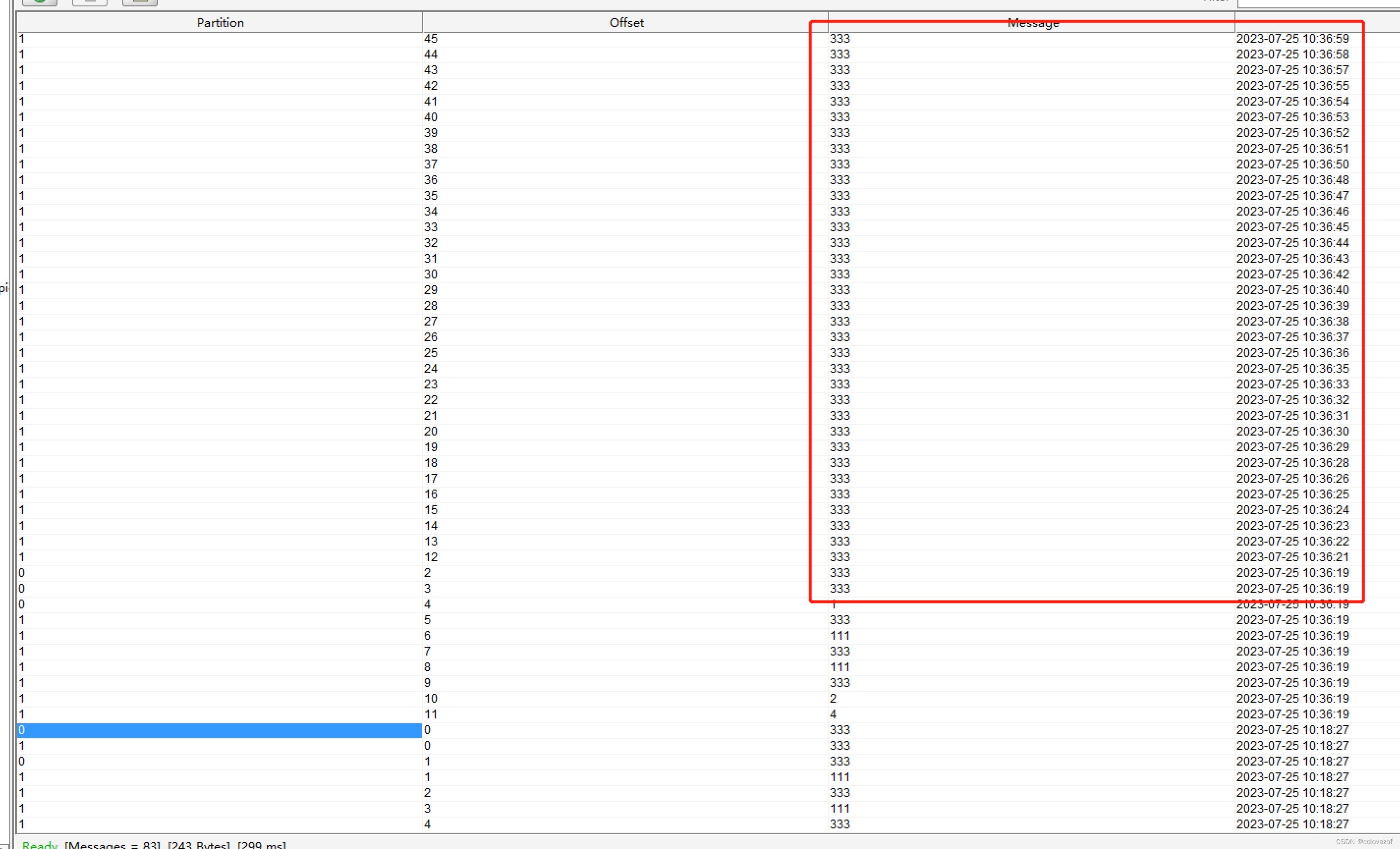
flink写入到kafka 大坑解析。
1.kafka能不能发送null消息? 能! 2 flink能不能发送null消息到kafka? 不能! public static void main(String[] args) throws Exception {StreamExecutionEnvironment env StreamExecutionEnvironment.getExecutionEnvironment(…...

MATLAB算法实战应用案例精讲-【深度学习】预训练模型-Subword
目录 前言 Subword 1. Subword介绍 分词器是做什么的? 为什么需要分词? 分词方法...
)
【HarmonyOS】实现从视频提取音频并保存到pcm文件功能(API6 Java)
【关键字】 视频提取类Extractor、视频编解码、保存pcm文件 【写在前面】 在使用API6开发HarmonyOS应用时,通常会开发一些音视频媒体功能,这里介绍如何从视频中提取音频保存到pcm文件功能,生成pcm音频文件后,就可使用音频播放类…...
Linux:shell命令运行原理和权限的概念
文章目录 shell和kernelshell的概念和原理Linux的权限文件的权限文件的类型文件的权限管理权限的实战应用 shell和kernel 从狭义上来讲,Linux是一个操作系统,我们叫它叫kernel,意思是核心,核心的意思顾名思义,就是最关…...

Javascript -- 数组prototype方法探究
一、数组prototype方法探究 1、不改变原数组 1. concat() 这个是数组拼接方法,可以将两个数组或多个数组拼接并返回一个包含两个数组或多个数组内容的新数组,不会改变原数组 方法里面理论上可以写入n个参数, const arr [1,2]; var str …...
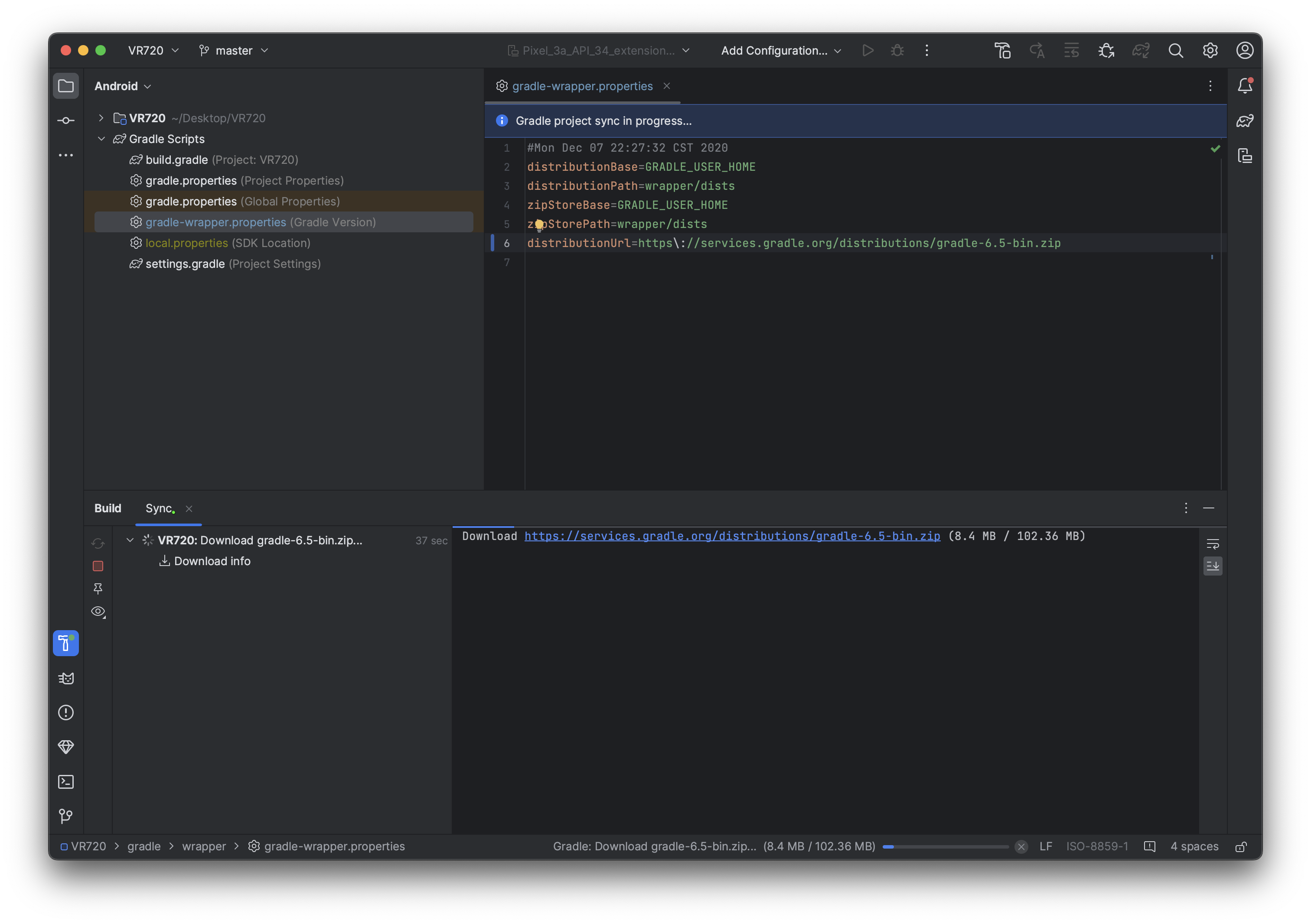
android stduio 打开工程后直接报Connection refused解决
报错如下:Connection refused 解决方案: 打开gradle-wrapper.properties修改distributionUrl 将: distributionUrlhttp\://localhost/gradle/distributions/gradle-6.5-bin.zip 替换为: distributionUrlhttps\://services.gradle.org/distributions/gradle-6.5-bin.zip 错…...

搜索与图论(一)
一、DFS与BFS 1.1深度优先搜索(DFS) DFS不具有最短性 //排列数字问题 #include<iostream> using namespace std;const int N 10; int n; int path[N]; bool st[N];void dfs(int u) {if(u n){for(int i 0;i < n;i) printf("%d",path[i]);puts("&qu…...

百题千解计划【CSDN每日一练】“小明投篮,罚球线投球可得一分”(附解析+多种实现方法:Python、Java、C、C++、C#、Go、JavaScript)
这个心上人,还不知道在哪里,感觉明天就会出现。 🎯作者主页: 追光者♂🔥 🌸个人简介: 💖[1] 计算机专业硕士研究生💖 🌟[2] 2022年度博客之星人工智能领域TOP4🌟 🏅[3] 阿里云社区特邀专家博主🏅 🏆[4] CSDN-人工智能领域优质创作者�…...

lemon框架开发笔记
lemon框架开发笔记 JudgeUtils.isBlank() 字符串为 null 或者 "" ----返回true JudgeUtils.isNotBlankAll() 字符串全部不为 null 或者 "" ----返回true JudgeUtils.isBlankAll() 字符串全部为 null 或者 "" ----返回true// isBlank 是在isEmpt…...

Spark SQL快速入门
1. 了解Spark SQL 1.1 什么是Spark SQL Spark SQL是spark的一个模块,用于处理海量的结构化数据。 1.2 Spark SQL有什么特点?优点是什么? 特点: Spark SQL支持读取和写入多种格式的数据源,包括Parquet、JSON、CSV、…...
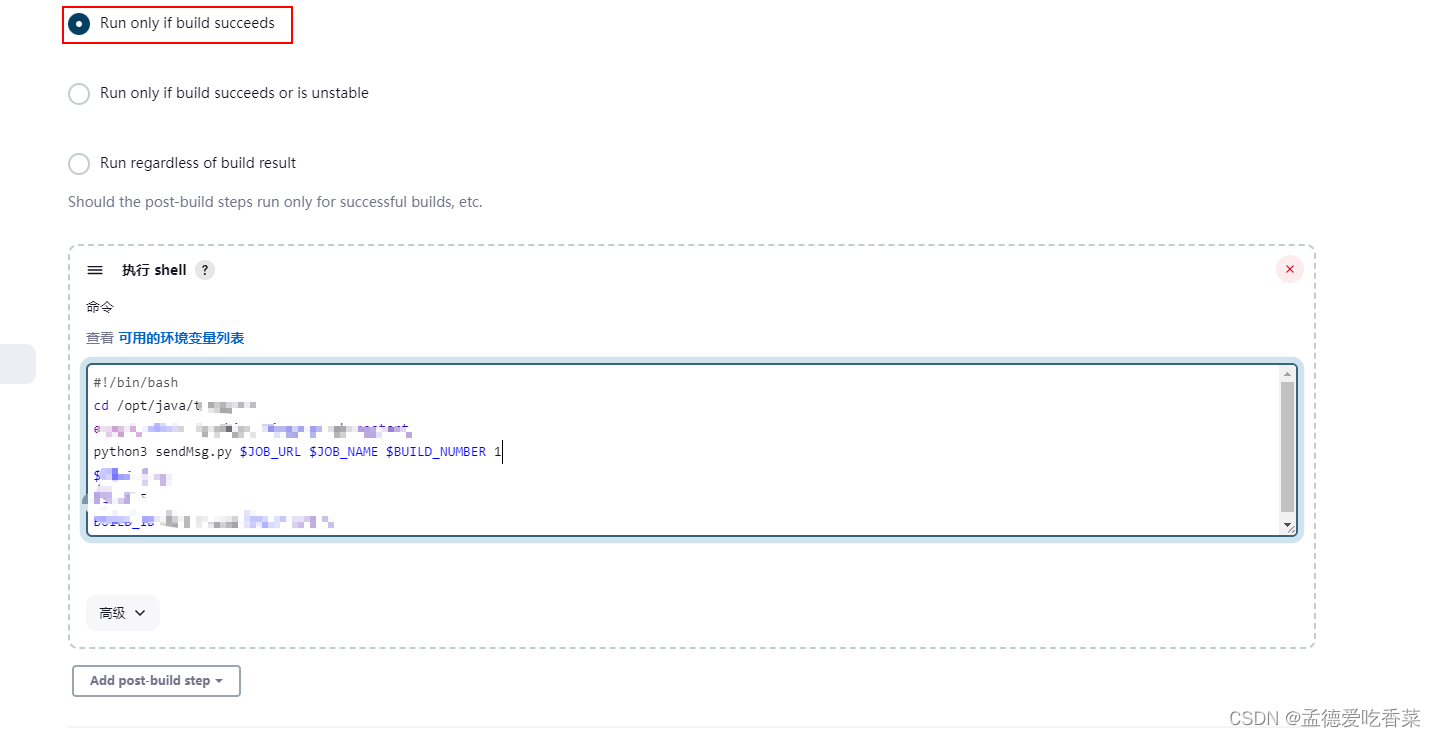
linux+Jenkins+飞书机器人发送通知(带签名)
文章目录 如何使用在linux 上安装python 环境发送消息python脚本把脚本上传倒linux上 jenkins 上执行脚本 如何使用 自定义机器人使用指南飞书官网https://open.feishu.cn/document/client-docs/bot-v3/add-custom-bot 在linux 上安装python 环境 yum install python3 python…...

react hooks
1 useEffect(setup,dependencies) 使用object.is来比较每个依赖项和它先前的值 依赖项为空数组的effect不会在组件任何props和state发生改变时重新运行 当useEffect依赖于外部传入props对象时,容易造成死循环 需要对依赖对象进行深比较 import { isEqual } from…...
一起学数据结构(1)——复杂度
目录 1. 时间复杂度: 1.1 时间复杂度的概念: 1.2 时间复杂度的表示及计算: 1.3 较为复杂的时间复杂度的计算: 2. 空间复杂度: 2.1 空间复杂度的概念: 2.2 空间复杂度的计算: 1. 时间复杂度…...
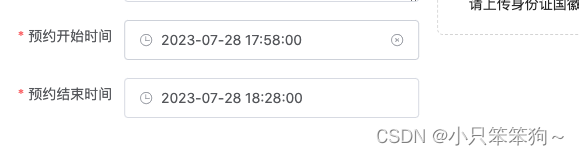
<el-date-picker>组件选择开始时间,结束时间自动延长30min
背景:选择开始时间,结束时间自动增加30分钟,结束时间也可重新选择,如图: <el-form-item label"预约开始时间" prop"value1"><el-date-pickersize"large"v-model"ruleForm…...

eslint-webpack-plugin
说明:现在eslint已经弃用了eslint-loader,如果要安装来使用的话,会报错,烦死人 大概的报错信息如下: ERROR in ./src/index.js Module build failed (from ./node_modules/eslint-loader/dist/cjs.js): TypeError: Cannot read …...

logback中文一直是乱码,logback中文问号
logback一直是乱码 方案一加上UTF-8 方案二我这边方案一不行 在启动参数加上 -Dfile.encodingutf-8 这个竟然就可以了...
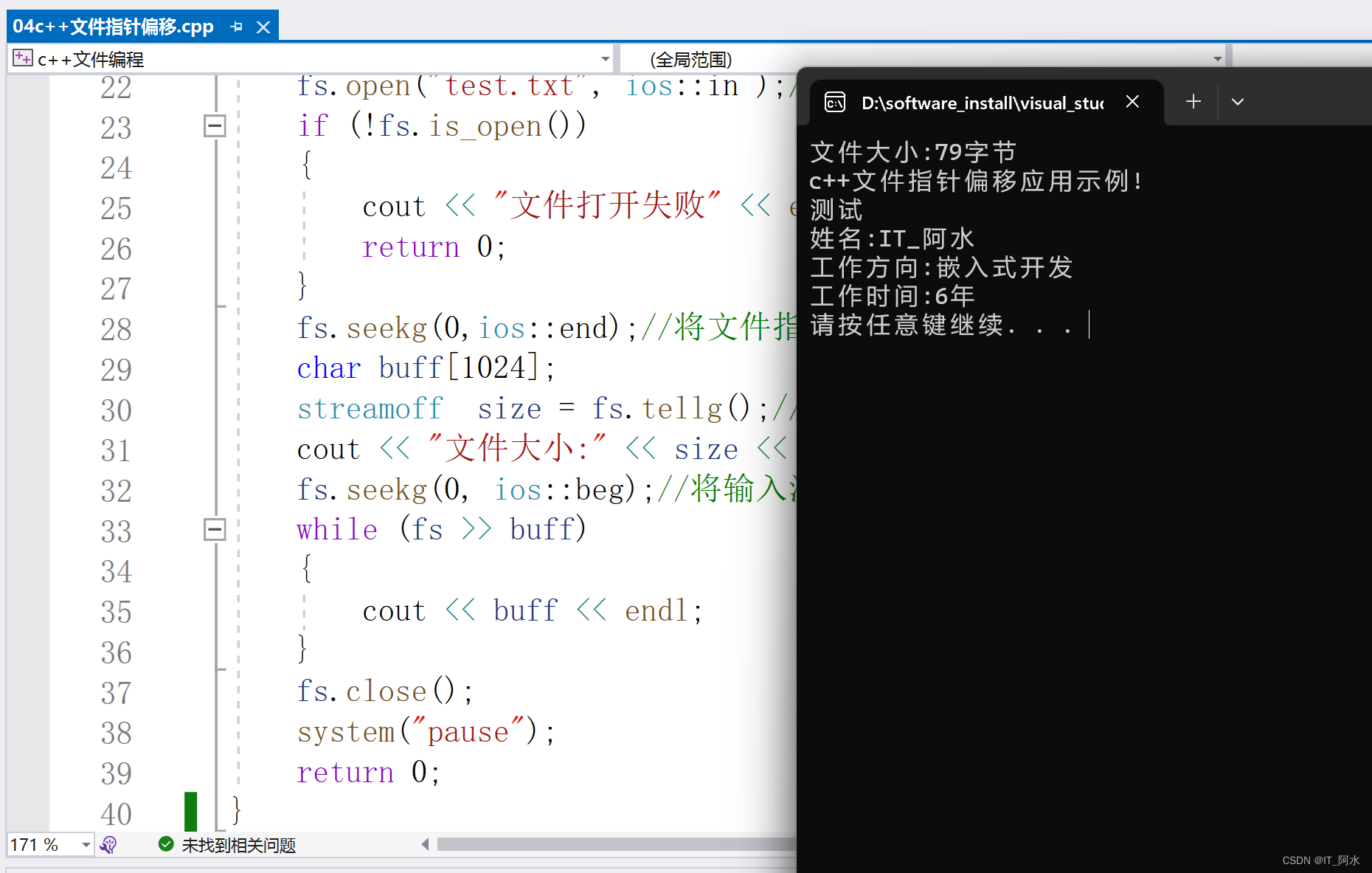
C++之文件操作
1.C文件操作 C中文件操作头文件:fstream。 文件类型:文件文件和二进制文件。 文件操作三大类: ofstream 写操作 ifstream 读操作 fstream:读写操作 文件打开方式: 标志说明ios::in只读ios::out只写,文件不存在则…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...
