搜索与图论(一)
一、DFS与BFS
1.1深度优先搜索(DFS)
DFS不具有最短性
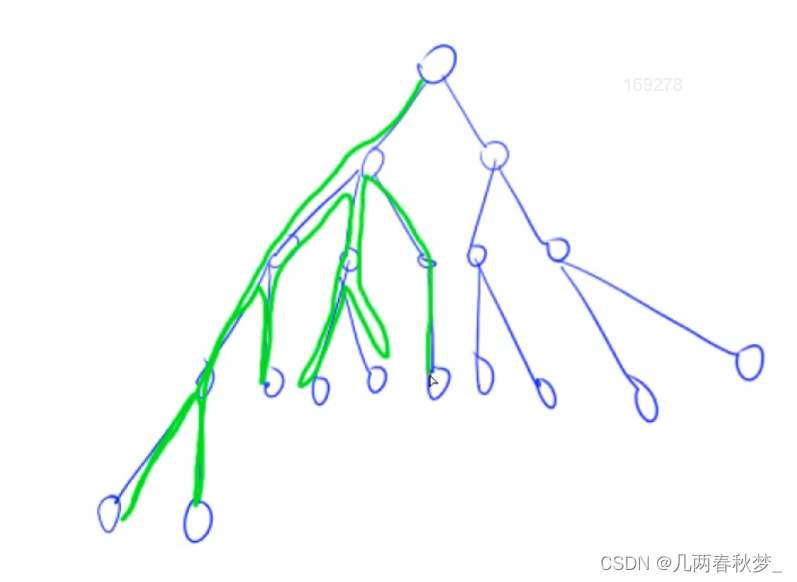
//排列数字问题
#include<iostream>
using namespace std;const int N = 10;
int n;
int path[N];
bool st[N];void dfs(int u)
{if(u == n){for(int i = 0;i < n;i++) printf("%d",path[i]);puts("");return;}for(int i =1;i <= n;i++){if(!st[i]){path[u] = i;st[i] = true;dfs(u + 1);st[i] = false;}}
}
int main()
{cin>>n;dfs(0);return 0;
}1.2宽度优先搜索(BFS)
一层一层搜索,可以搜到最短路。
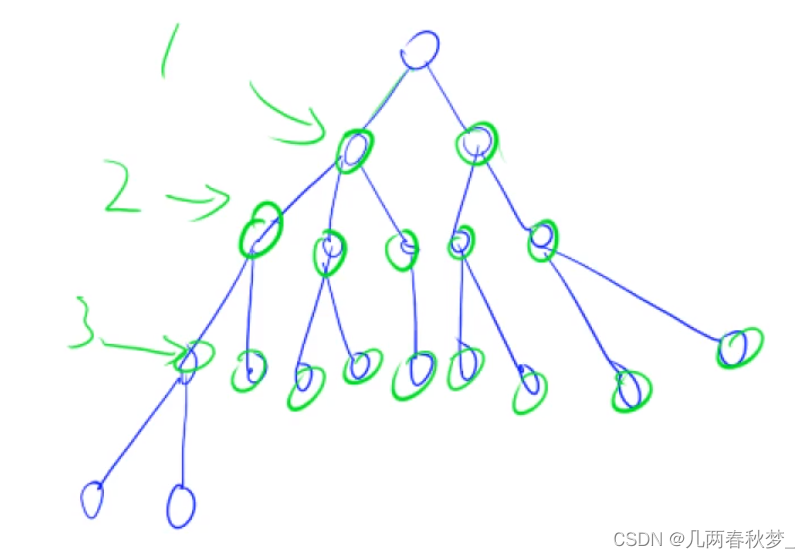
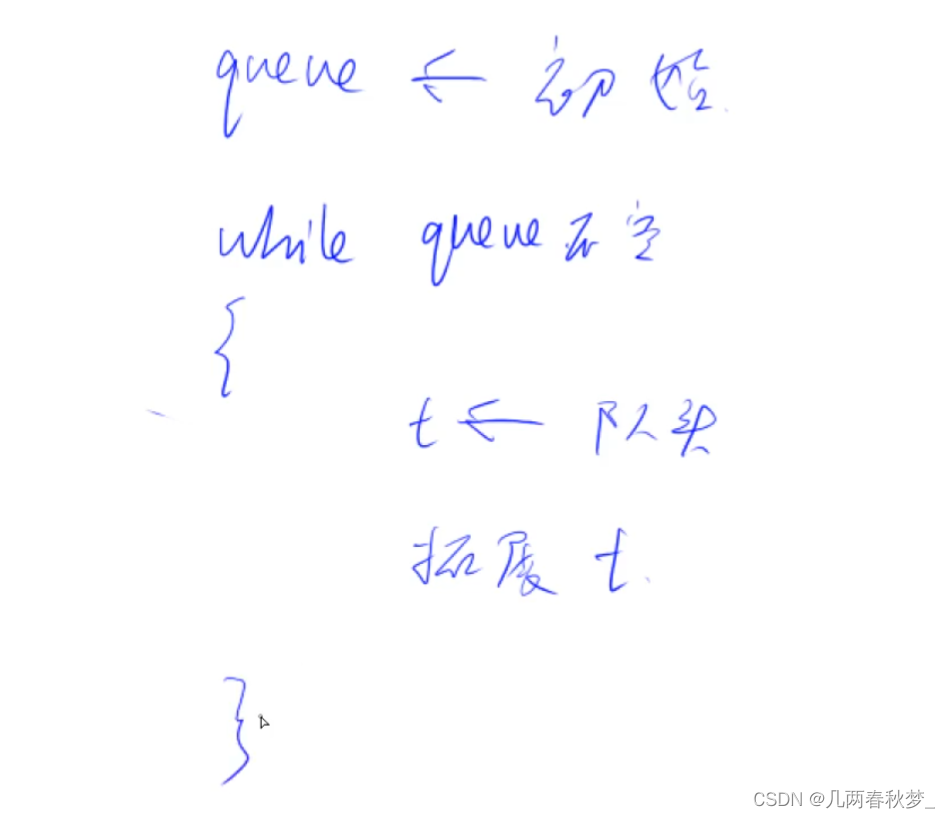
//走迷宫问题
#include<iostream>
#include<algorithm>
#include<queue>
#include<cstring>
using namespace std;typedef pair<int,int> PII;const int N = 110;int n,m;
int g[N][N];
int d[N][N];
PII q[N * N];int bfs()
{int hh = 0,tt = 0;q[0] = {0,0};//初始化为-1memset(d,-1,sizeof d);d[0][0] = 0;//定义头的向量int dx[4] = {-1,0,1,0},dy[4] = {0,1,0,-1};while(hh <= tt){auto t = q[hh ++];for(int i = 0; i< 4;i++){int x = t.first + dx[i],y = t.second + dy[i];if(x >=0 && x < n && y >= 0 && y < m && g[x][y] ==0 && d[x][y] == -1){d[x][y] = d[t.first][t.second] + 1;q[++ tt] = {x,y};}}}return d[n - 1][m - 1];
}int main()
{cin>>n>>m;for(int i = 0;i < n;i++)for(int j = 0;j < m;j++)cin>>g[i][j];cout<<bfs()<<endl;return 0;
}
二、树与图的遍历
2.1树与图的深度优先遍历
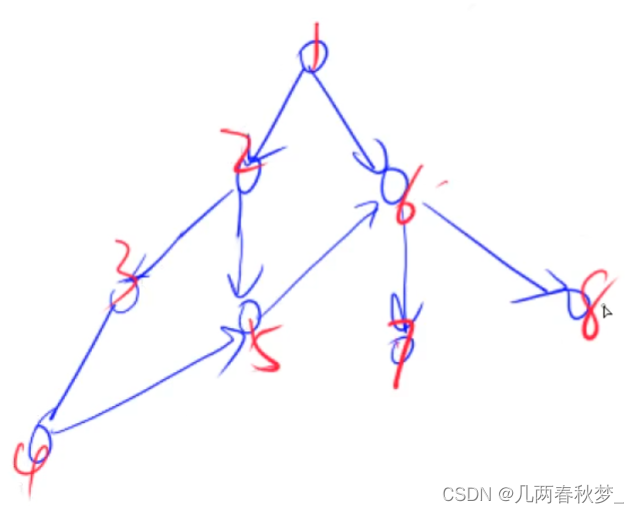
#include<iostream>
using namespace std;int n,m;
//h存的是n个链表的链表头
//e存的是所有的结点值
//ne存的是每个节点的next指针
int h[N],e[M],ne[M],idx;
bool st[N];void dfs(int u)
{stu[u] = true; //标记一下,已经被搜过了for(int i = h[u];i != -1;i = ne[i]){int j = e[i];if(!st[j]) dfs(j);}
}2.2树与图的广度优先遍历

int n,m;
int h[N],e[N],ne[N],idx;
//d是距离,q是队列
int d[N],q[N];//插入函数
void add(int a,int b)
{e[idx] = b,ne[idx],ne[idx] = h[a],h[a] = idx++;
}
int bfs()
{//定义队头队尾int hh = 0,tt = 0;q[0] = 1;memset(d,-1,sizeof d);d[1] = 0;while(hh <= tt){int t = q[hh ++];for(int i = h[t];i != -1;i = ne[i]){int j = e[i];if(d[j] == -1){d[j] = d[t] + 1;q[++ tt] = j;}}}return d[n];
}三、拓扑排序
适用于有向图

#include<cstring>
#include<iostream>
#include<algorithm>using namespace std;const int N = 100010;int n,m;
int h[N],e[N],ne[N],idx;
//q为队列,d为存储的入度
int q[N],d[N];void add(int a,int b)
{e[idx] = b,ne[idx] = h[a],h[a] = idx++;
}bool topsort()
{int hh = 0,tt = -1;for(int i =1;i <= n;i++){if(!d[i])q[++tt] = i;}while(hh <= tt){int t = q[hh++];for(int i = h[t];i!=-1;i = ne[i]){int j = e[i];d[j]--;if(d[j] == 0) q[++tt] = j;}}return tt == n-1;
}
int main()
{cin>>n>>m;memset(h,-1,sizeof h);for(int i = 0;i < m;i++){int a,b;cin>>a>>b;add(a,b);}if(topsort()){for(int i =0;i < n;i++) printf("%d",q[i]);puts("");}else{puts("-1");}return 0;
}
相关文章:

搜索与图论(一)
一、DFS与BFS 1.1深度优先搜索(DFS) DFS不具有最短性 //排列数字问题 #include<iostream> using namespace std;const int N 10; int n; int path[N]; bool st[N];void dfs(int u) {if(u n){for(int i 0;i < n;i) printf("%d",path[i]);puts("&qu…...

百题千解计划【CSDN每日一练】“小明投篮,罚球线投球可得一分”(附解析+多种实现方法:Python、Java、C、C++、C#、Go、JavaScript)
这个心上人,还不知道在哪里,感觉明天就会出现。 🎯作者主页: 追光者♂🔥 🌸个人简介: 💖[1] 计算机专业硕士研究生💖 🌟[2] 2022年度博客之星人工智能领域TOP4🌟 🏅[3] 阿里云社区特邀专家博主🏅 🏆[4] CSDN-人工智能领域优质创作者�…...

lemon框架开发笔记
lemon框架开发笔记 JudgeUtils.isBlank() 字符串为 null 或者 "" ----返回true JudgeUtils.isNotBlankAll() 字符串全部不为 null 或者 "" ----返回true JudgeUtils.isBlankAll() 字符串全部为 null 或者 "" ----返回true// isBlank 是在isEmpt…...

Spark SQL快速入门
1. 了解Spark SQL 1.1 什么是Spark SQL Spark SQL是spark的一个模块,用于处理海量的结构化数据。 1.2 Spark SQL有什么特点?优点是什么? 特点: Spark SQL支持读取和写入多种格式的数据源,包括Parquet、JSON、CSV、…...
linux+Jenkins+飞书机器人发送通知(带签名)
文章目录 如何使用在linux 上安装python 环境发送消息python脚本把脚本上传倒linux上 jenkins 上执行脚本 如何使用 自定义机器人使用指南飞书官网https://open.feishu.cn/document/client-docs/bot-v3/add-custom-bot 在linux 上安装python 环境 yum install python3 python…...

react hooks
1 useEffect(setup,dependencies) 使用object.is来比较每个依赖项和它先前的值 依赖项为空数组的effect不会在组件任何props和state发生改变时重新运行 当useEffect依赖于外部传入props对象时,容易造成死循环 需要对依赖对象进行深比较 import { isEqual } from…...
一起学数据结构(1)——复杂度
目录 1. 时间复杂度: 1.1 时间复杂度的概念: 1.2 时间复杂度的表示及计算: 1.3 较为复杂的时间复杂度的计算: 2. 空间复杂度: 2.1 空间复杂度的概念: 2.2 空间复杂度的计算: 1. 时间复杂度…...
<el-date-picker>组件选择开始时间,结束时间自动延长30min
背景:选择开始时间,结束时间自动增加30分钟,结束时间也可重新选择,如图: <el-form-item label"预约开始时间" prop"value1"><el-date-pickersize"large"v-model"ruleForm…...

eslint-webpack-plugin
说明:现在eslint已经弃用了eslint-loader,如果要安装来使用的话,会报错,烦死人 大概的报错信息如下: ERROR in ./src/index.js Module build failed (from ./node_modules/eslint-loader/dist/cjs.js): TypeError: Cannot read …...

logback中文一直是乱码,logback中文问号
logback一直是乱码 方案一加上UTF-8 方案二我这边方案一不行 在启动参数加上 -Dfile.encodingutf-8 这个竟然就可以了...
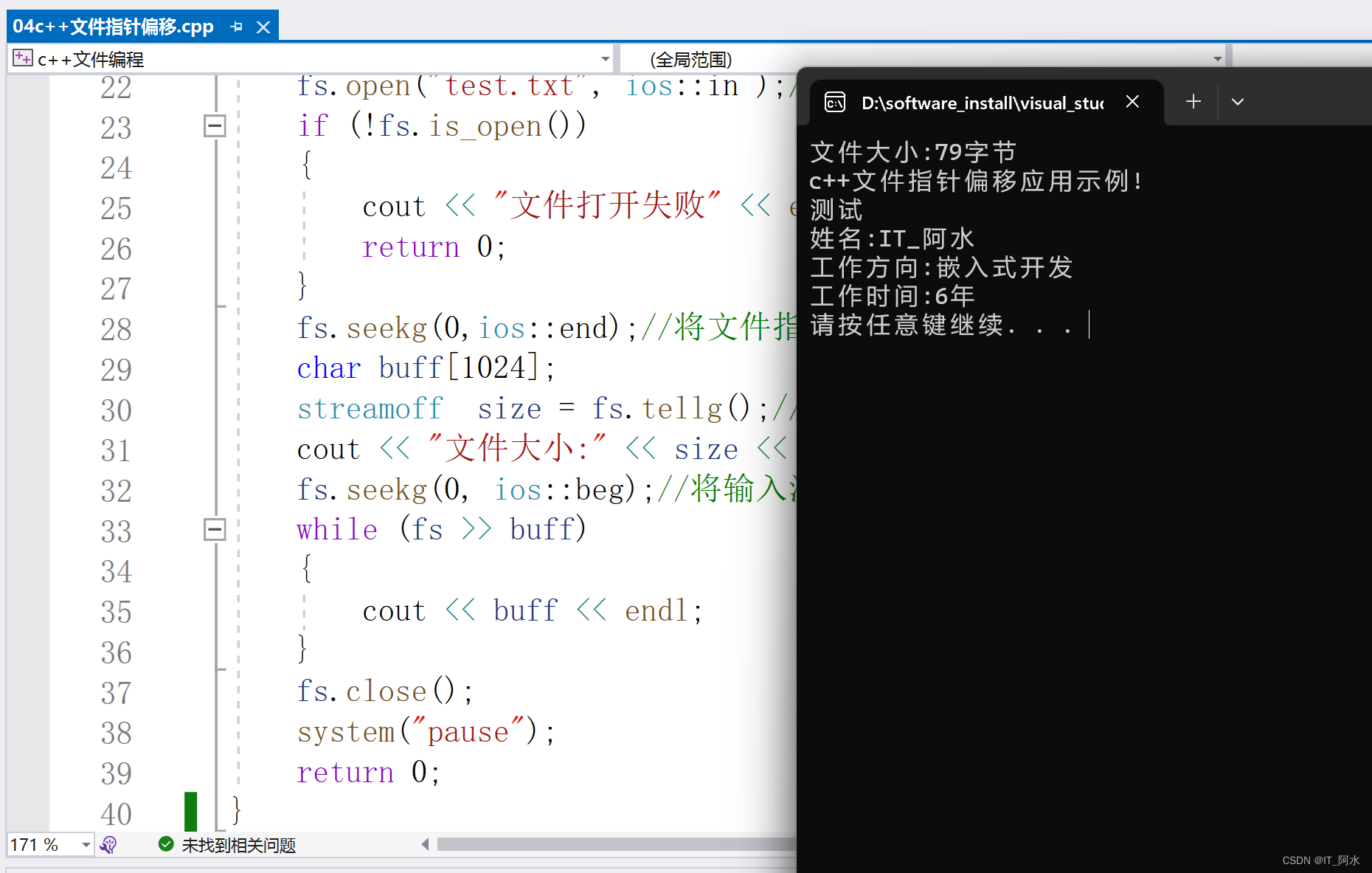
C++之文件操作
1.C文件操作 C中文件操作头文件:fstream。 文件类型:文件文件和二进制文件。 文件操作三大类: ofstream 写操作 ifstream 读操作 fstream:读写操作 文件打开方式: 标志说明ios::in只读ios::out只写,文件不存在则…...

CentOS 7.6安装 MongoDB 5.0.2
https://developer.aliyun.com/article/983777 我遇到的问题:如何以集群的方式启动,使用replSet的方式进行启动: 需要在配置文件上加上replSet的信息 port27017 #端口 bind_ip0.0.0.0 #默认是127.0.0.1 dbpath/usr/local/mongodb/data #数据…...
Windows下安装python3教程
参考:https://blog.csdn.net/kailingr/article/details/128193083 一、安装步骤图解 准备工作: 进官网https://www.python.org/下载Python 安装包,注意:Python 3.9不能在Windows 7或更早版本上使用 安装: 1.下载完之后双击该文…...
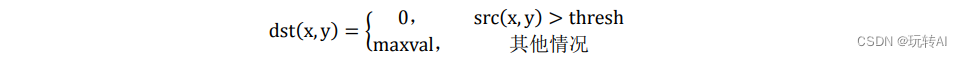
opencv-27 阈值处理 cv2.threshold()
怎么理解阈值处理? 阈值处理(Thresholding)是一种常用的图像处理技术,在机器学习和计算机视觉中经常被用于二值化图像或二分类任务。它基于设定一个阈值来将像素值进行分类,将像素值大于或小于阈值的部分分为两个不同的类别&…...
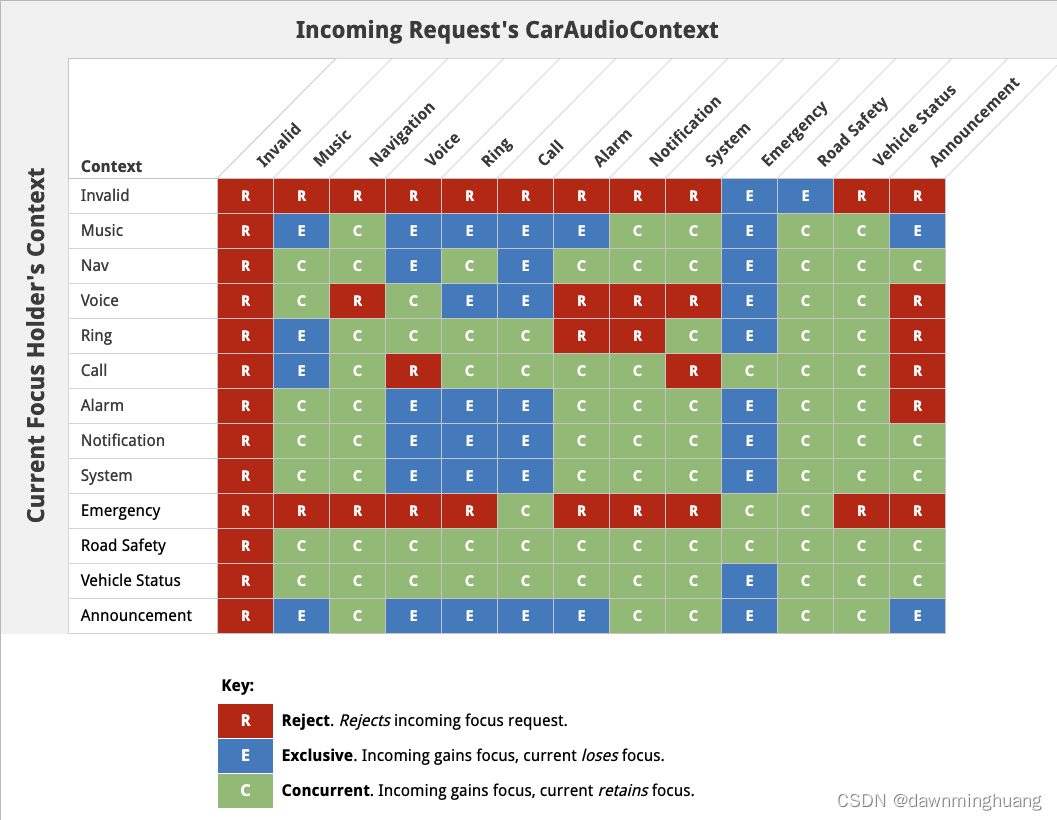
AAOS 音频焦点请求
文章目录 前言基本概念提供给应用来获取音频焦点的apiAAOS中的音频焦点管理交互矩阵duck的实现流程AAOS 测试应用kitchensink焦点相关 前言 本文章的目标是首先了解Android中音频焦点的基本概念,理解代码中相关音频焦点的使用方法。其次理解AAOS 中相关交互矩阵概念…...

订单系统中的幂等实现
一.订单提交的例子 一个订单生成并支付的过程,大致为:用户点击前端页面提交订单->后端根据此次提交信息生成订单->用户确认订单并进行支付操作->支付成功。 主要分为前端层面,后端系统层面,数据库层面。前端层面不详述…...
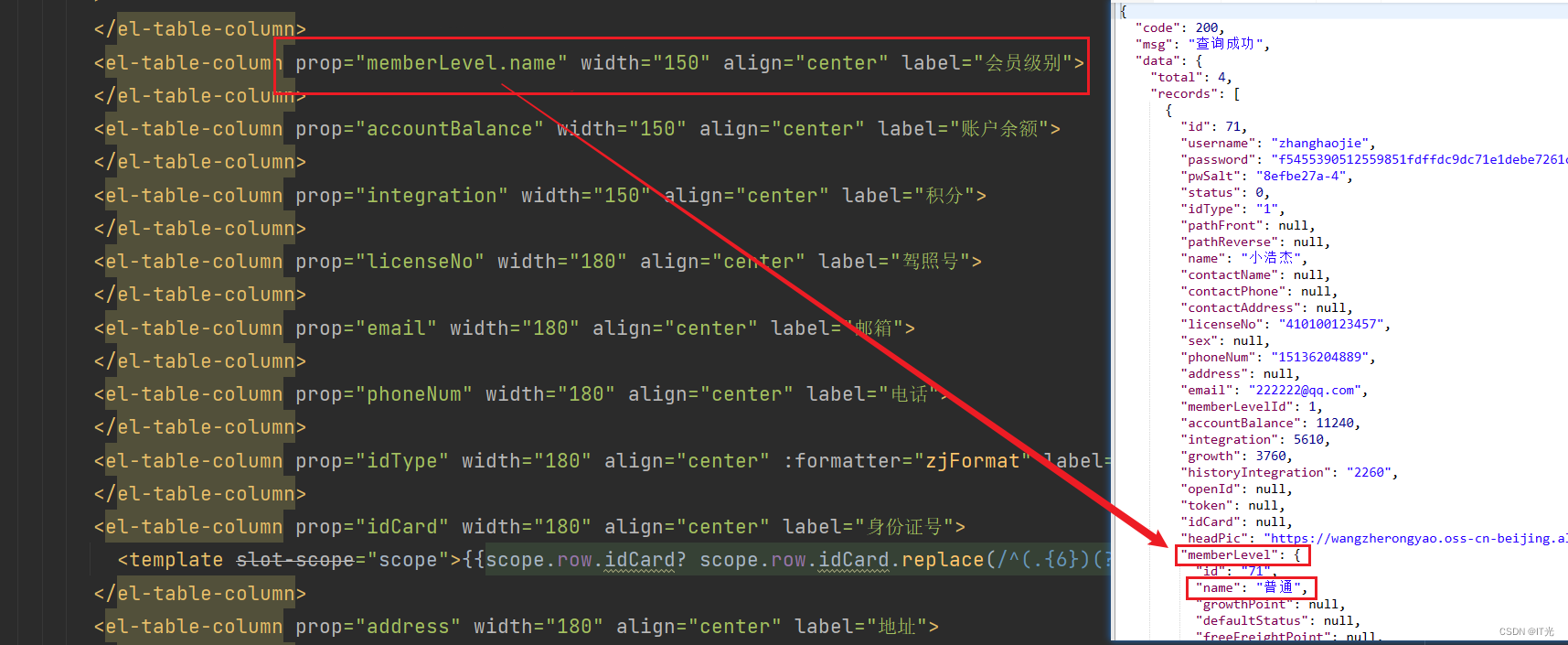
三个常用查询:根据用户名 / token查询用户信息+链表分页条件查询
目录 1.根据用户名或者token查询用户信息 会员信息实体类 统一状态Result类 controller层 service层及实现类 dao层 测试: 2.链表分页条件查询 会员等级实体类 封装条件类PageVo controller层 service层及实现类 dao层 Mapper.xml层 测试 vue前端参考 1.根据用户名…...

列表、张量、向量和矩阵的关系
在数学和编程中,列表、张量、向量和矩阵之间有一定的关系。这些概念在不同领域和语境中有略微不同的定义和用法,以下是它们之间的一般关系: 列表(List): 列表是编程语言中的一种数据结构,用于存…...
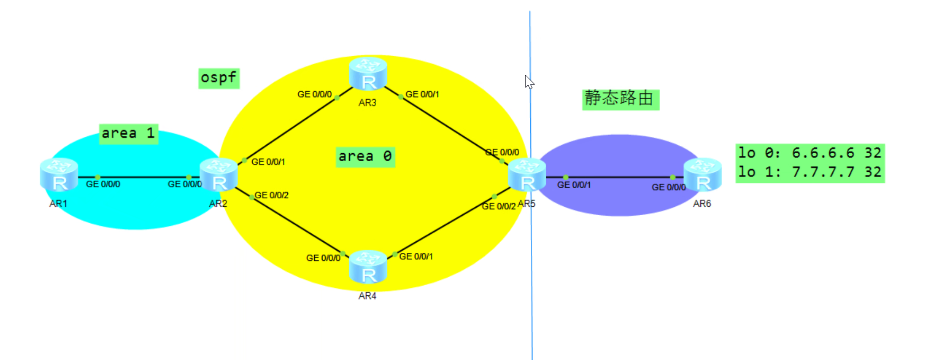
华为数通HCIP-ISIS高级
isis区域间的互访 1、L2区域 to L1区域 在L1区域发布的路由会以L1-LSP在L1区域内传递,到达L1-2路由器时,L1-2路由器会将该L1-LSP转换为L2-LSP在L2区域内传递; 因此L2区域的设备可以学习到L1区域的明细路由,进行访问;…...
CorelDraw怎么做立体字效果?CorelDraw制作漂亮的3d立体字教程
1、打开软件CorelDRAW 2019,用文本工具写上我们所需要的大标题。建议字体选用比较粗的适合做标题的字体。 2、给字填充颜色,此时填充的颜色就是以后立体字正面的颜色。我填充了红色,并加上了灰色的描边。 3、选中文本,单击界面左侧…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...
