清风学习笔记—层次分析法—matlab对判断矩阵的一致性检验
在判断矩阵是否为正互反矩阵这块,我写了两种代码,改进前很麻烦且有错误,改进后简洁多了,改进前的代码还有错误,忽略了对角线的值必须都是1,只考虑了除开对角线的元素相乘为1。
%% 改进前代码
A=[3 2 4;1/2 4 2;1/4 1/2 5]
diag_A=diag(A)
C=ones(1,size(A,2))
%将矩阵A的对角线更改为全1向量C
A(logical(eye(size(A))))=C
%获取矩阵A的共轭转置矩阵A2
A2=A.'
%如果A2和A进行点乘能够得到一个单位矩阵,那么A就是一个正互反矩阵
if isequal(A2.*A,ones(size(A,1)))fprintf("A是一个正互反矩阵")
end
%将矩阵A的主对角线进行还原
A(logical(eye(size(A))))=diag_A%% 改进后代码
if sum(sum(A'.*A~=ones(n)))>0error=3;disp("不为正互反矩阵")
end下面是全部代码
%% 输入判断矩阵
clear;clc
disp('请输入判断矩阵A: ')
A = input('判断矩阵A=');
[r,c]=size(A);
error=0;
%% 判断矩阵是否为方阵并且阶数大于等于2
if r~=c || r<2error=1;
end
%% 判断矩阵是否大于15
if r==c&&r>15error=2;
end%% 判断矩阵A是否为正互反矩阵
if error~=1 && sum(sum(A'.*A~=ones(r)))>0error=3;
end
%% 计算
if error==0%% 算术平均法求权重Sum_A = sum(A);[n,m] = size(A);SUM_A = repmat(Sum_A,n,1);Stand_A = A ./ SUM_A;sum(Stand_A,2);disp('算术平均法求权重的结果为:');disp(sum(Stand_A,2) ./ n)%% 方法2:几何平均法求权重Prduct_A = prod(A,2);Prduct_n_A = Prduct_A .^ (1/n);disp('几何平均法求权重的结果为:');disp(Prduct_n_A ./ sum(Prduct_n_A));%% 方法3:特征值法求权重[V,D] = eig(A);Max_eig = max(max(D));[r,c] = find(D == Max_eig , 1);V(:,c);disp('特征值法求权重的结果为:');disp( V(:,c) ./ sum(V(:,c)) )%% 计算一致性比例CRCI = (Max_eig - n) / (n-1);RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59]; %注意哦,这里的RI最多支持 n = 15CR=CI/RI(n);disp('一致性指标CI=');disp(CI);disp('一致性比例CR=');disp(CR);if CR<0.10disp('因为CR < 0.10,所以该判断矩阵A的一致性可以接受!');elsedisp('注意:CR >= 0.10,因此该判断矩阵A需要进行修改!');end
elseif error==1disp("输入的A不为方阵或者阶数小于2")
elseif error==2disp("判断矩阵的阶数大于15")
elseif error==3disp("不为正互反矩阵")
end
相关文章:

清风学习笔记—层次分析法—matlab对判断矩阵的一致性检验
在判断矩阵是否为正互反矩阵这块,我写了两种代码,改进前很麻烦且有错误,改进后简洁多了,改进前的代码还有错误,忽略了对角线的值必须都是1,只考虑了除开对角线的元素相乘为1。 %% 改进前代码 A[3 2 4;1/2 …...

大众安徽内推
大众汽车(安徽)有限公司是大众汽车集团在中国第一家专注于新能源汽车的合资企业,是集团在中国首家拥有全面运营管理权的合资企业,担负着产品研发及数字化研发的重任,将成为集团全球电动出行中心之一。 VW Anhui Offic…...

Meta “地平线世界”移动端应用即将上线,手机快乐元宇宙?
根据海外记者 Janko Roettgers 的报道,Meta 预计很快推出移动版的 VR 元宇宙服务 "地平线世界",这是Meta 长期开发的产品。 根据最新报道,Meta宣布正在研发“地平线世界”的移动版,并表示这一服务已经可以在Quest VR设…...

更省更快更安全的云服务器,一站式集中管理,随时随地远程——站斧云桌面
随着全球化和数字化经济的发展,越来越多的企业开始海外扩张和拓展国际市场。而云服务器作为一种高效、灵活且可靠的IT基础设施方案,已成为出海企业不可或缺的重要工具。这里就为大家介绍云服务器在出海企业中的几个使用场景。 1.全球范围内协同办公 对…...
 的解决方法)
出现 Try run Maven import with -U flag (force update snapshots) 的解决方法
目录 1. 问题所示2. 原理分析3. 解决方法1. 问题所示 在配置Maven依赖信息的时候,出现如下问题: com.alibaba.nacos:nacos‐client:pom:1.1.3 failed to transfer from http://nexus.hepengju.cn:8081/nexus/content/groups/public/ during a previous attempt. This failu…...

python多线程
目录 一.多线程的定义 A.什么是多线程? B.多线程如今遇到的挑战 C.总结 二.python中的多线程 A.python中的多线程底层原理: B.全局解释器锁导致python多线程不能实现真正的并行执行! C.总结应用场景 三.java多线程,以及…...

Spring Framework 提供缓存管理器Caffeine
说明 Spring Framework 提供了一个名为 Caffeine 的缓存管理器。Caffeine 是一个基于 Java 的高性能缓存库,被广泛用于处理大规模缓存数据。 使用 Caffeine 缓存管理器,可以轻松地在 Spring 应用程序中添加缓存功能。它提供了以下主要特性:…...

ZQC的游戏 题解
前言 这题题意描述不是很清楚啊,所以我找了个有权限的人把题面改了改,应该还是比较清楚了。 感觉这道题挺妙的,就来写一篇题解。 思路 首先,根据贪心思想,我们会将 1 1 1 号点半径以内能吃的都吃了,假…...
24考研数据结构-第一章 绪论
数据结构 引用文章第一章:绪论1.0 数据结构在学什么1.1 数据结构的基本概念1.2 数据结构的三要素1.3 算法的基本概念1.4 算法的时间复杂度1.4.1 渐近时间复杂度1.4.2 常对幂指阶1.4.3 时间复杂度的计算1.4.4 最好与最坏时间复杂度 1.5 算法的空间复杂度1.5.1 空间复…...
Gitlab 备份与恢复
备份 1、备份数据(手动备份) gitlab-rake gitlab:backup:create2、备份数据(定时任务备份) [rootlocalhost ]# crontab -l 00 1 * * * /opt/gitlab/bin/gitlab-rake gitlab:backup:create 说明:每天凌晨1点备份数据…...
数据库—用户权限管理(三十三)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 一、概述 二、用户权限类型 三、用户赋权 四、权限删除 五、用户删除 前言 数据库用户权限管理是指对数据库用户的权限进行控制和管理,确保用户只能执…...

C语言【怎么定义变量?】
变量定义的目的是向编译器说明在哪里创建变量的存储,并指明如何创建变量的存储方式。变量定义会明确指定一个数据类型,并包含一个或多个变量的列表。例如: type variable_list; 在这里,"type"必须是一个合法的C数据类…...

vue中使用vab-magnifier实现放大镜效果
效果图如下: 1. 首先,使用npm或yarn安装vab-magnifier插件: npm install vab-magnifier或 yarn add vab-magnifier2. 在Vue组件中引入vab-magnifier插件: import VabMagnifier from vab-magnifier; import vab-magnifier/lib…...

无涯教程-jQuery - Highlight方法函数
Highlight 效果可以与effect()方法一起使用。这将以特定的颜色突出显示元素的背景,默认为黄色(yellow)。 Highlight - 语法 selector.effect( "highlight", {arguments}, speed ); 这是所有参数的描述- color - 高亮显示颜色。默认值为"#fff…...
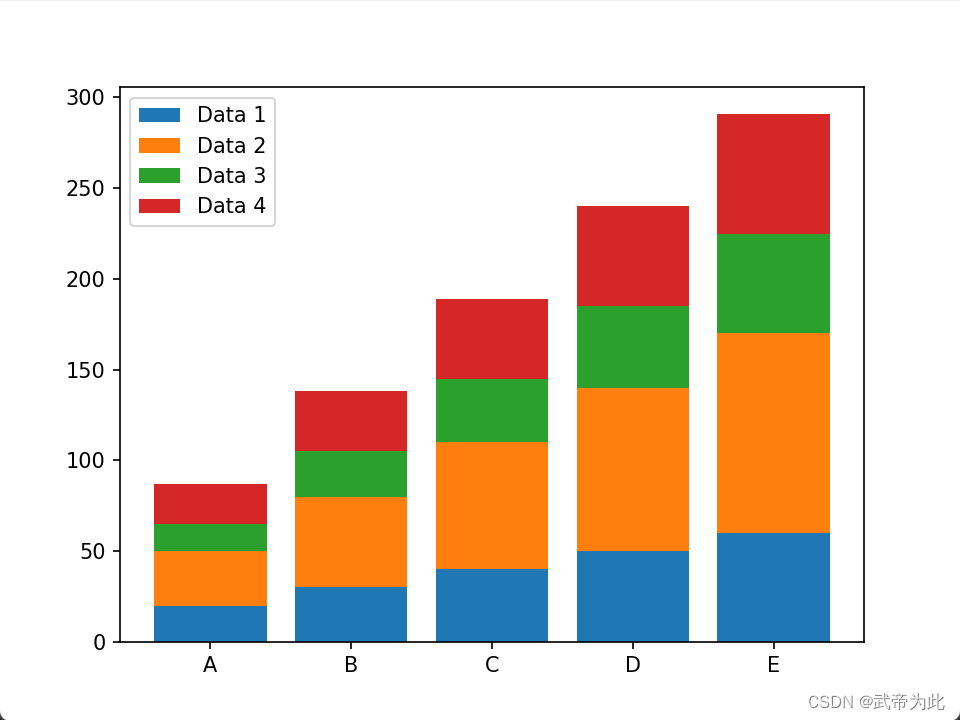
【bar堆叠图形绘制】
绘制条形图示例 在数据可视化中,条形图是一种常用的图表类型,用于比较不同类别的数据值。Python的matplotlib库为我们提供了方便易用的功能来绘制条形图。 1. 基本条形图 首先,我们展示如何绘制基本的条形图。假设我们有一个包含十个类别的…...
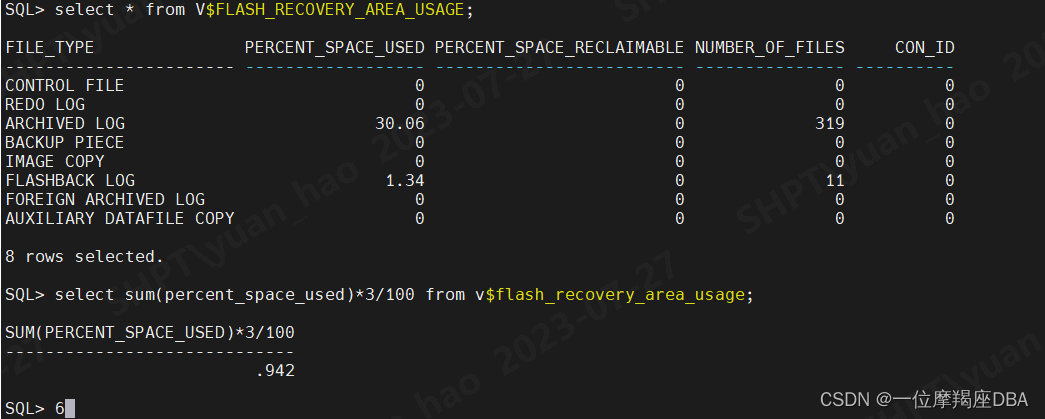
ORACLE数据库灾难恢复
一:RMAN恢复 .1 创建测试用户,授权,分配测试表空间,给测试数据 –创建测试用户: SQL> alter session set containerPRODPDB; Session altered. SQL> SQL> show con_name; CON_NAME PRODPDB SQL> cre…...

base和正则备份
js图片网络地址转file文件_朱1只的博客-CSDN博客 JavaScript 图片url地址转base64_图片地址转base64_vanora1111的博客-CSDN博客 前端常用正则表达式(详细版)_前端正则表达式匹配字符串_Ultraman_agul的博客-CSDN博客...
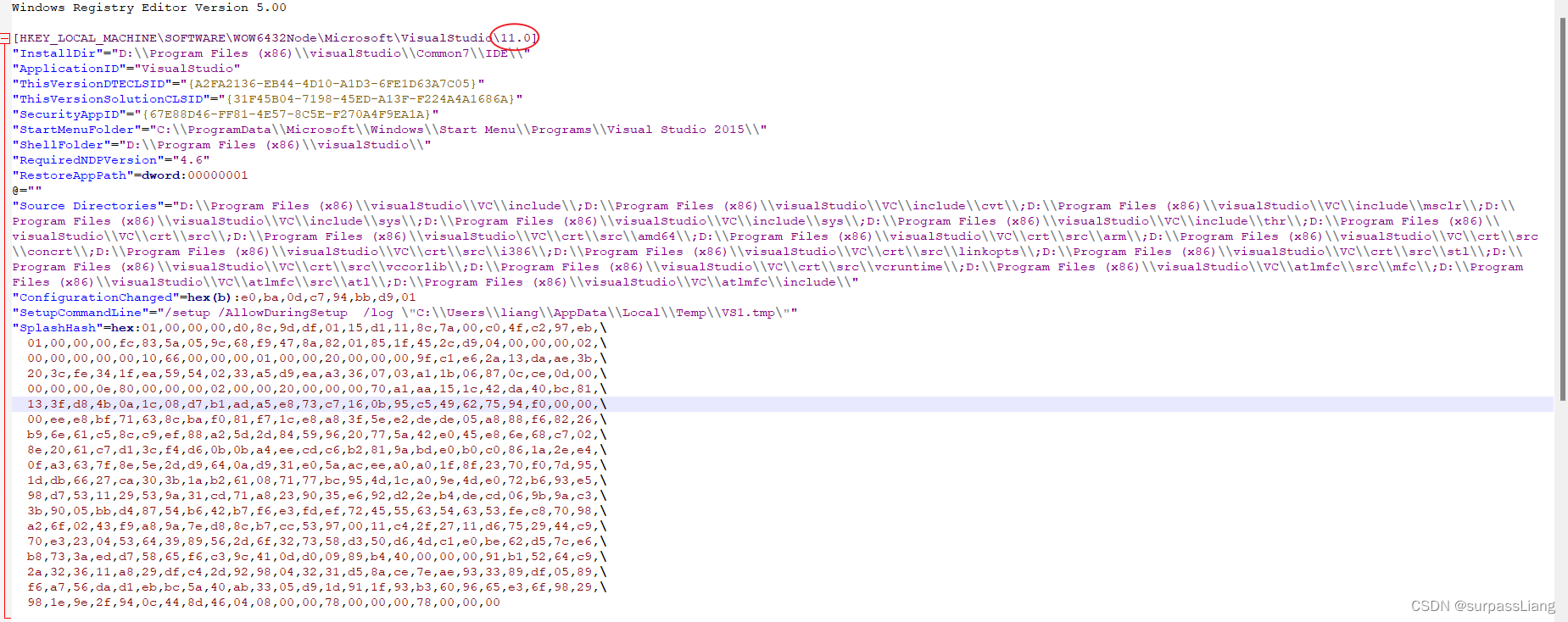
ArcGIS Engine 与 Visual Studio版本对照表
通过C#对于Arcgis的二次开发,需要Visual Studio版本需要与ArcGIS Engine对应,Visual Studio版本的或高或低都不能使ArcObjects SDK for microsoft.Net framework安装成功。下面是各个版本的对照表。 序号ArcEngine版本visual Studio版本Network版本110.…...
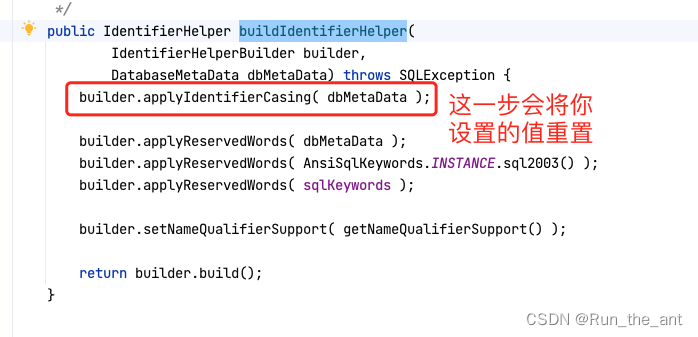
JPA连接达梦数据库导致auto-ddl失效问题解决
现象: 项目使用了JPA,并且auto-ddl设置的为update,在连接达梦数据库的时候,第一次启动没有问题,但是后面重启就会报错,发现错误为重复建表,也就是说已经建好的表没有检测到,…...
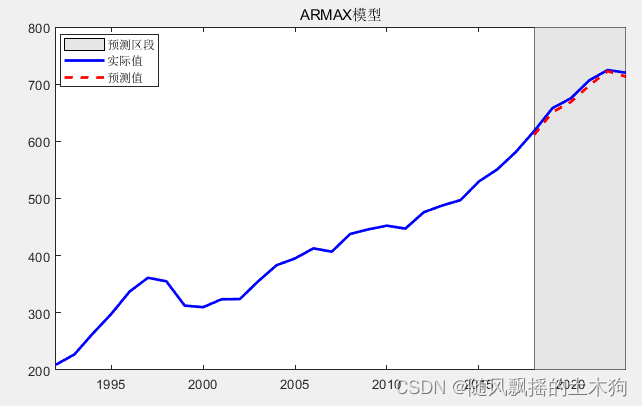
【MATLAB第60期】【更新中】基于MATLAB的ARMAX具有外生回归因子的移动平均自回归模型
【MATLAB第60期】【更新中】基于MATLAB的ARMAX具有外生回归因子的移动平均自回归模型 版本更新: 2023/7/29版本: 1.增加自定义参数,方便直接套数据运行。 pre_num3;%预采样数据个数 learn_pr0.85; %训练数据比例(不包括预采样数…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...

DeepSeek越强,Kimi越慌?
被DeepSeek吊打的Kimi,还有多少人在用? 去年,月之暗面创始人杨植麟别提有多风光了。90后清华学霸,国产大模型六小虎之一,手握十几亿美金的融资。旗下的AI助手Kimi烧钱如流水,单月光是投流就花费2个亿。 疯…...
