Pearson correlation皮尔逊相关性分析
在参数检验的相关性分析方法主要是皮尔逊相关(Pearson correlation)。既然是参数检验方法,肯定是有一些前提条件。皮尔逊相关的前提是必须满足以下几个条件:
- 变量是连续变量;
- 比较的两个变量必须来源于同一个总体;
- 没有异常值;
- 两个变量都符合正态分布。
正态分布的呈现是倒“U”型曲线。在实际分析过程中,想要一份数据同时满足以上条件,确实是有一定难度的。毕竟我们是没法保证收上来的数据,一定恰好是符合正态分布的。
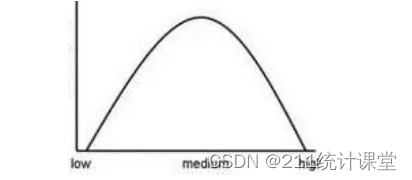
皮尔逊相关系数的范围是位于[-1,1]之间。相关系数展示了方向性:
- 如果相关系数接近1,说明两个变量之间呈较高的正相关性;
- 如果相关系数接近-1,说明两个变量之间呈较高的负相关性;
- 如果相关系数接近0,说明两个变量之间彼此独立,没有相关性。
皮尔逊相关的结果包括两个值,相关系数和P值。在相关性分析中,P值代表着两个变量是否显著相关。
一般而言,分析结果里,我们先看P值。如果P值小于0.05,那么两个变量呈显著的相关性。
然后再看相关系数的方向性,报告两个变量是显著的正相关或负相关。
SPSS操作详细步骤
第一步,选择“分析”——“相关”——“双变量”。
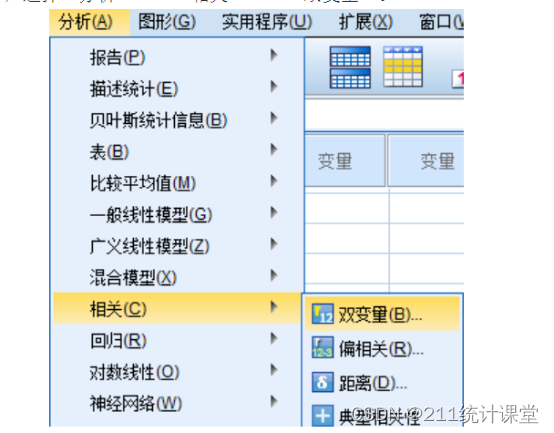
第二步,在相关系数里,选择“皮尔逊”。显著性可以选“双侧”。
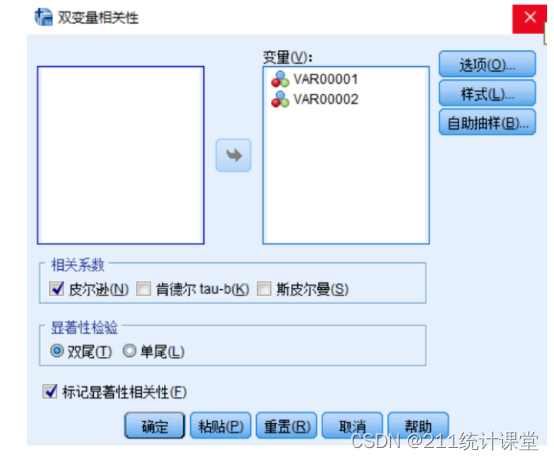
第三步,点击“选项”,可以勾选统计,计算平均数与标准差等,如下图所示。
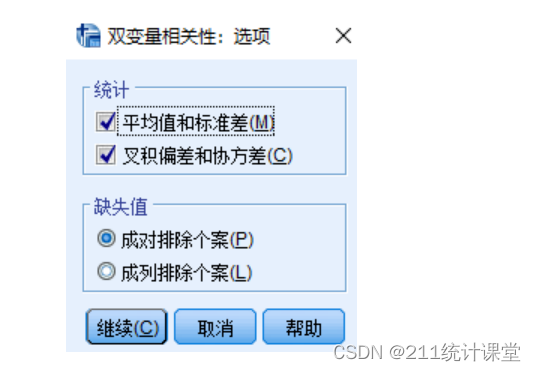
其他设置都可以默认。直接点“确定”,就能生成结果了。
如果想要保留SPSS语法文件,可以先点击“粘贴”,保存本次所有操作,如图5.4所示。下次还要执行同样的操作,直接全选以后,点击绿色小三角符号,就可以生成皮尔逊分析结果了。
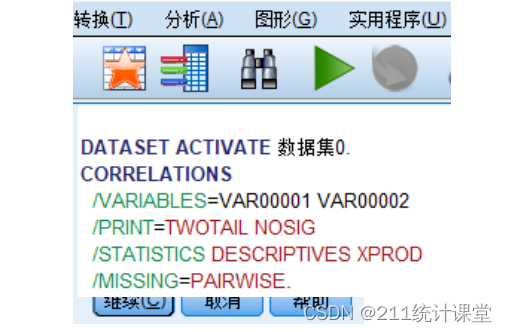
皮尔逊相关性分析结果显示,P值显著性为0.222,如红框中所示。P值大于0.05,说明示例的两个变量无显著相关性。相关性系数为0.265,离1比较远,也说明相关性不高。
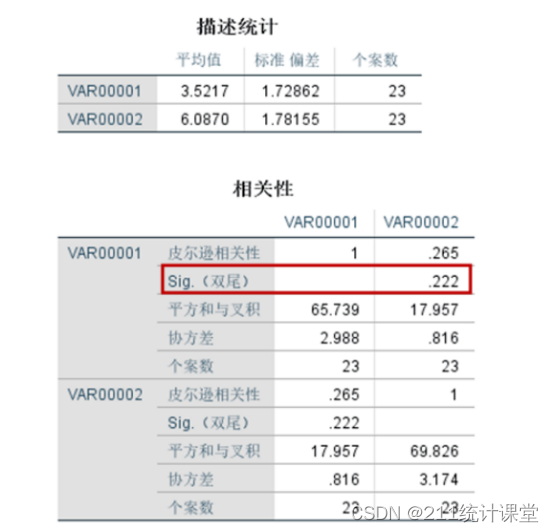
以上就是皮尔逊相关性分析的内容。
相关文章:

Pearson correlation皮尔逊相关性分析
在参数检验的相关性分析方法主要是皮尔逊相关(Pearson correlation)。既然是参数检验方法,肯定是有一些前提条件。皮尔逊相关的前提是必须满足以下几个条件: 变量是连续变量;比较的两个变量必须来源于同一个总体&…...

P1036 [NOIP2002 普及组] 选数
题目描述 已知 �n 个整数 �1,�2,⋯ ,��x1,x2,⋯,xn,以及 11 个整数 �k(�<�k<n)。从 �n 个整数中任选 �k 个…...

css终极方案PostCSS
一见如故 原理 所有的css框架都在一样的事,那就是由一个css生成一个新的css,那么postcss就来做了一个抽离: 1、将原有的css解析成抽象语法树 2、中间经过若干个插件 3、重新文本化,形成新的css postcss.config.js module.expor…...

代码随想录算法训练营第三天|417. 太平洋大西洋水流问题|24. 两两交换链表中的节点|19.删除链表的倒数第N个节点|面试题 02.07. 链表相交|
417. 太平洋大西洋水流问题 水往高处流,先记录两个海祥往高处流所能留到的地址,之后将他们的合并区域进行输出 static const int dirs[4][2] {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};class Solution { public:vector<vector<int>> heights;v…...
【Java】Spring——创建Spring + 对Spring的存储 /读取对象操作
文章目录 前言一、创建Spring项目二、向Spring容器中存储 Bean 对象三、从Spring容器中读取 Bean 对象得到Spring上下文对象得到 Bean 对象 总结 前言 本人是一个普通程序猿!分享一点自己的见解,如果有错误的地方欢迎各位大佬莅临指导,如果你也对编程感兴趣的话,互…...

RTPSv2.2(中文版)
实时发布订阅协议 (RTPS) DDS互操作性 有线协议规范 V2.2 (2014-09-01正式发布) https://www.omg.org/spec/DDSI-RTPS/2.2/PDF 目 录 1 范围Scope 9 2 一致性Conformance 9 3 参考文献References 9 4 术语和定义Terms a…...
Django学习笔记-视图(views)的使用
Django中可以使用views进行管理,类似于WPF的MVVM的ViewModel层,也相当于MVC架构的模Controller层。 一、基于函数的视图FBV(Function-Based View) 通过定义一个函数,包含HttpRequest对象作为参数,用来接受…...
四姑娘山三日游
趁着小孩放暑假,从昆明回来之后,直接自驾到四姑娘山。 第一天 成都-四川省阿坝藏族羌族自治州小金县日隆镇(20230711) 大概9:30从成都市郫都区出发,路线如下:郫都—都江堰–映秀—耿达—卧龙—四姑娘山,中途翻过巴朗…...
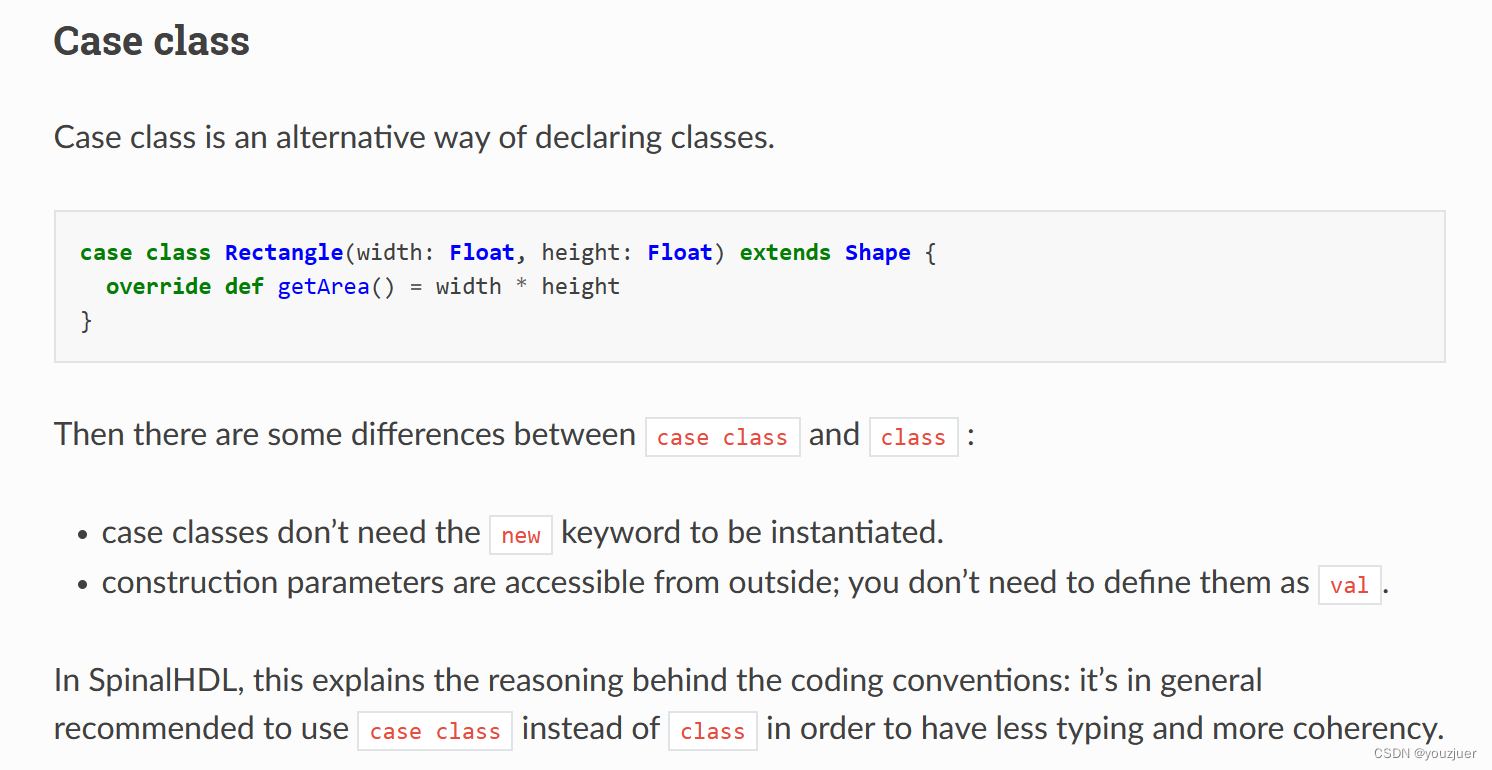
spinal HDL语法学习
1 赋值语句 用来声明变量 : 用来对变量进行赋值 2 when otherwise前面是否有"."与otherwise是否换行有关系 3 case class 对Bundle进行扩展时,需要case class case class和class主要有两点区别: (1)case class不需…...

GRE TAP的工作原理与5G工业物联网中的应用
随着互联网新技术的发展以及智能化水平的提高,各企业对实时数据传输的需求也在不断提升,企业愈发重视数据中心的建设,以保障企业内网数据安全。 GRE(Generic Routing Encapsulation,通用路由封装)协议属于…...
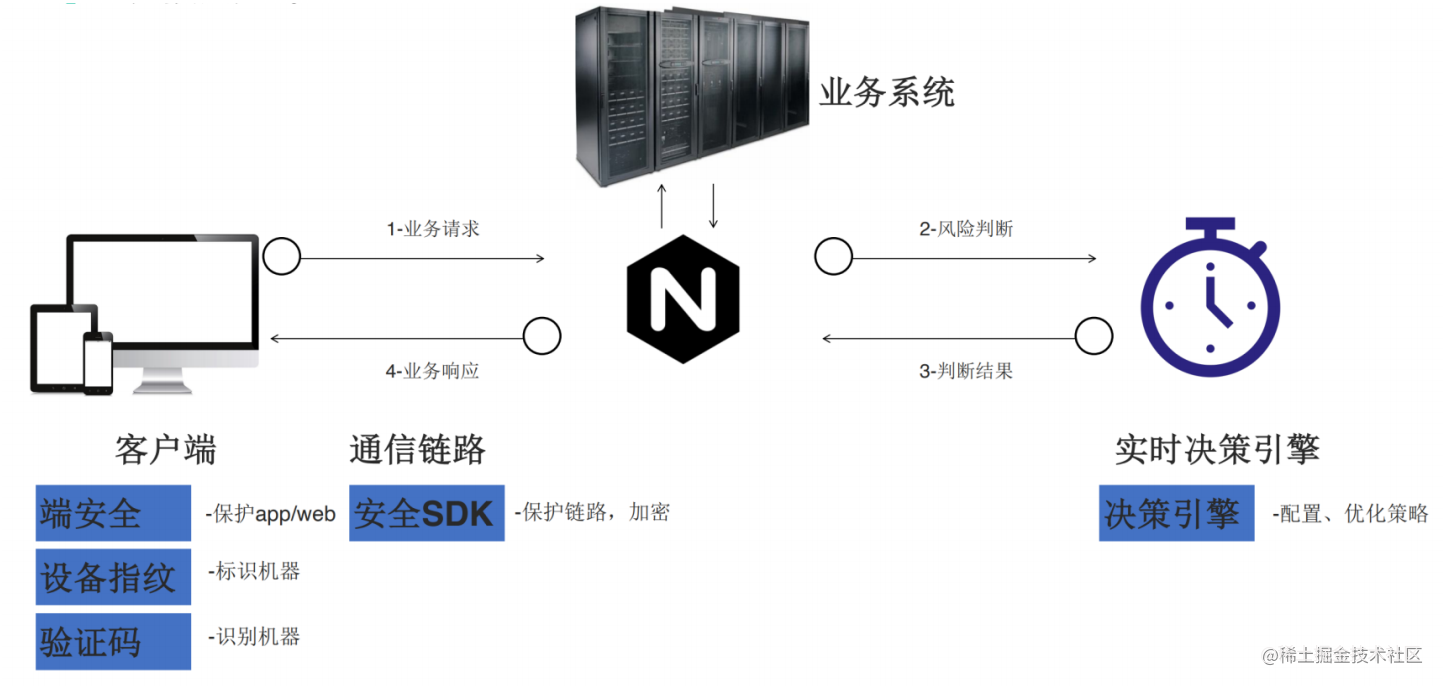
NFT和数字藏品的安全方案解析
一、NFT和数字藏品 01 NFT是什么? NFT 是Non-Fungible Tokens 的缩写,意思是不可互换的代币,它是相对于可互换的代币而言的。不可互换的代币也称为非同质代币。什么是可互换的代币?比如BTC(比特币)、ETH&…...
第四篇-Miniconda3-CentOS7-安装
Miniconda3-CentOS7-安装 Conda可以创建你需要的不同版本的Python环境,做的各个环境之间隔离,可以有助于我们一台主机部署不同版本运行环境 下载 wget https://repo.anaconda.com/miniconda/Miniconda3-latest-Linux-x86_64.sh执行 sh Miniconda3-latest-Linux-…...
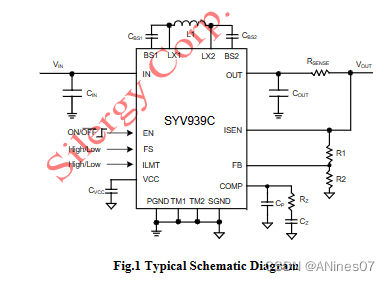
高效率,38V最大输入单电感同步升/降稳压器SYV939C
SYV939是一种高压同步降压-升压转换器。该器件工作在4V至28V的宽输入电压范围内,具有10max平均电感电流能力。四个集成的低RDS(ON)开关最大限度地减少了传导损耗。 SYV939c包括完整的保护功能,如输出过流/短路保护,过压保护和热停机ÿ…...
mars3d绘制区域范围(面+边框)
1、图例(绿色面区域白色边框) 2、代码 1)、绘制区域ts文件 import { mapLayerCollection } from /hooks/cesium-map-init /*** 安全防護目標* param map*/ export const addSafetyProtection async (map) > {const coverDatas await m…...

HTML的表格应用
HTML 中的表格用于在网页上展示和组织数据。表格由行和列组成,每个单元格可以包含文本、图像或其他 HTML 元素。下面是一些常用的 HTML 表格标签和属性的应用示例: <table> 标签: 定义表格的起始和结束标记。所有的表格元素应该放在这对标签之间。…...

android的数据存储方式
android的数据存储方式 Android提供了多种数据存储方式,开发者可以根据具体的需求选择合适的存储方式。以下是Android中常用的数据存储方式: Shared Preferences(共享偏好设置): Shared Preferences允许将简单的键值…...

用C++编写一个MyString类
1.平台:vs2019 2.很多知识点写在了代码里 class MyString { private:char* str;MyString(char* p, int x){str p;} public:MyString(const char* p nullptr) :str(nullptr){if (p ! nullptr){int len strlen(p) 1;str new char[len];strcpy_s(str, len, p);}…...

Linux C语言中access函数的用法
access()函数的用法:int access(const char *filenpath, int mode) 一、access()函数的作用 access()函数用来判断某个指定路径的文件(第一个参数 filenpath),是否符合第二个参数选项(F_OK(文件是否存在)…...

c# winform 子窗体关闭时主窗体执行指令
按下一个按钮打开子窗体,点 x 关闭子窗体后主窗体自动执行某些指令。例如刷新窗体,加载数据等。 点 x 关闭子窗体后将会执行"刷新父窗体2"下面的内容,其他的没试。 Config readConfigTest new Config();//new一个子窗体并打开 re…...

vue-simple-uploader的fileAdded方法不支持异步的解决办法,autoStart 设置
每日鸡汤:悲观者可能正确,但是乐观者往往成功 假设有一个需求,上传的pdf文档不得大于10M 使用 vue-simple-uploader 这个插件,我们需要在 fileAdded 事件里面进行校验,在1.0.0版本以后,如果想停止上传&…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...
