随笔:hhhhh
第一题
∫ − ∞ + ∞ x e x − e x d x = ∫ 0 + ∞ ln t ⋅ e ln t − t ⋅ 1 t d t = ∫ 0 + ∞ ln t ⋅ e − t ⋅ 1 t ⋅ t d t = ∫ 0 + ∞ ln t ⋅ e − t d t = ψ ( 1 ) = − γ \begin{align*} \int_{-\infty}^{+\infty}xe^{x-e^x}\text{d}x&=\int_{0}^{+\infty} \ln t \cdot e^{\ln t - t} \cdot \frac{1}{t} \text{d}t \\ &= \int_{0}^{+\infty} \ln t \cdot e^{ - t} \cdot \frac{1}{t} \cdot t \text{d}t\\ & = \int_{0}^{+\infty} \ln t \cdot e^{-t} \text{d}t=\psi(1)\\&=-\gamma \end{align*} ∫−∞+∞xex−exdx=∫0+∞lnt⋅elnt−t⋅t1dt=∫0+∞lnt⋅e−t⋅t1⋅tdt=∫0+∞lnt⋅e−tdt=ψ(1)=−γ
第二题
∫ 0 + ∞ x 4 e x ( e x − 1 ) 2 d x = − ∫ 0 + ∞ x 4 d 1 e x − 1 = 4 ∫ 0 + ∞ x 3 e x − 1 d x − x 4 e x − 1 ∣ 0 + ∞ = 4 ∫ 0 + ∞ x 3 e − x 1 − e − x d x = 4 ∫ 0 + ∞ ( x 3 ∑ n = 1 + ∞ e − n x ) d x = 4 ∑ n = 1 + ∞ ( ∫ 0 + ∞ x 3 e − n x d x ) = 4 ∑ n = 1 + ∞ [ − ( 1 n x 3 + 3 n 2 x 2 + 6 n 3 x + 6 n 4 ) e − n x ∣ 0 + ∞ ] = 24 ∑ n = 1 + ∞ 1 n 4 = 4 π 4 15 \begin{align*} \int_{0}^{+\infty}&\frac{x^{4}e^{x}}{(e^{x}-1)^{2}}dx\\ =&-\int_{0}^{+\infty}x^{4}d\frac{1}{e^{x}-1}\\ =&4\int_{0}^{+\infty}\frac{x^{3}}{e^{x}-1}dx-\frac{x^{4}}{e^{x}-1}\big|_{0}^{+\infty}\\ =&4\int_{0}^{+\infty}\frac{x^{3}e^{-x}}{1 - e^{-x}}dx\\ =&4\int_{0}^{+\infty}\left(x^{3}\sum_{n = 1}^{+\infty}e^{-nx}\right)dx\\ =&4\sum_{n = 1}^{+\infty}\left(\int_{0}^{+\infty}x^{3}e^{-nx}dx\right)\\ =&4\sum_{n = 1}^{+\infty}\left[-\left(\frac{1}{n}x^{3}+\frac{3}{n^{2}}x^{2}+\frac{6}{n^{3}}x+\frac{6}{n^{4}}\right)e^{-nx}\big|_{0}^{+\infty}\right]\\ =&24\sum_{n = 1}^{+\infty}\frac{1}{n^{4}}\\ =&\frac{4\pi^{4}}{15} \end{align*} ∫0+∞========(ex−1)2x4exdx−∫0+∞x4dex−114∫0+∞ex−1x3dx−ex−1x4 0+∞4∫0+∞1−e−xx3e−xdx4∫0+∞(x3n=1∑+∞e−nx)dx4n=1∑+∞(∫0+∞x3e−nxdx)4n=1∑+∞[−(n1x3+n23x2+n36x+n46)e−nx 0+∞]24n=1∑+∞n41154π4
第三题
对于直角应变花,试证明主应变的大小及方向可用以下公式计算:
ε max ε min } = ε 0 ∘ + ε 9 0 ∘ 2 ± 2 2 ( ε 0 ∘ − ε 4 5 ∘ ) 2 + ( ε 4 5 ∘ − ε 9 0 ∘ ) 2 \left. \begin{array}{l} \varepsilon_{\max} \\ \varepsilon_{\min} \end{array} \right\} = \frac{\varepsilon_{0^{\circ}} + \varepsilon_{90^{\circ}}}{2} \pm \frac{\sqrt{2}}{2} \sqrt{(\varepsilon_{0^{\circ}} - \varepsilon_{45^{\circ}})^2 + (\varepsilon_{45^{\circ}} - \varepsilon_{90^{\circ}})^2} εmaxεmin}=2ε0∘+ε90∘±22(ε0∘−ε45∘)2+(ε45∘−ε90∘)2
tan 2 α 0 = 2 ε 4 5 ∘ − ε 0 ∘ − ε 9 0 ∘ ε 0 ∘ − ε 9 0 ∘ \tan 2\alpha_{0} = \frac{2\varepsilon_{45^{\circ}} - \varepsilon_{0^{\circ}} - \varepsilon_{90^{\circ}}}{\varepsilon_{0^{\circ}} - \varepsilon_{90^{\circ}}} tan2α0=ε0∘−ε90∘2ε45∘−ε0∘−ε90∘
6 0 ∘ 60^{\circ} 60∘应变花,三个应变片的角度分别为: α 1 = 0 ∘ , α 2 = 6 0 ∘ , α 3 = 12 0 ∘ \alpha_{1}=0^{\circ}, \alpha_{2}=60^{\circ}, \alpha_{3}=120^{\circ} α1=0∘,α2=60∘,α3=120∘。求证主应变的数值及方向由以下公式计算:
ε max ε min } = ε 0 ∘ + ε 6 0 ∘ + ε 12 0 ∘ 3 ± 2 3 ( ε 0 ∘ − ε 6 0 ∘ ) 2 + ( ε 6 0 ∘ − ε 12 0 ∘ ) 2 + ( ε 12 0 ∘ − ε 0 ∘ ) 2 \left. \begin{array}{l} \varepsilon_{\max} \\ \varepsilon_{\min} \end{array} \right\} = \frac{\varepsilon_{0^{\circ}} + \varepsilon_{60^{\circ}} + \varepsilon_{120^{\circ}}}{3} \pm \frac{\sqrt{2}}{3} \sqrt{(\varepsilon_{0^{\circ}} - \varepsilon_{60^{\circ}})^2 + (\varepsilon_{60^{\circ}} - \varepsilon_{120^{\circ}})^2 + (\varepsilon_{120^{\circ}} - \varepsilon_{0^{\circ}})^2} εmaxεmin}=3ε0∘+ε60∘+ε120∘±32(ε0∘−ε60∘)2+(ε60∘−ε120∘)2+(ε120∘−ε0∘)2
tan 2 α 0 = 3 ( ε 6 0 ∘ − ε 12 0 ∘ ) 2 ε 0 ∘ − ε 6 0 ∘ − ε 12 0 ∘ \tan 2\alpha_{0} = \frac{\sqrt{3}(\varepsilon_{60^{\circ}} - \varepsilon_{120^{\circ}})}{2\varepsilon_{0^{\circ}} - \varepsilon_{60^{\circ}} - \varepsilon_{120^{\circ}}} tan2α0=2ε0∘−ε60∘−ε120∘3(ε60∘−ε120∘)
证明
对于以上问题我们有
ε α 1 = ε x + ε y 2 + ε x − ε y 2 cos 2 α 1 + γ x y 2 sin 2 α 1 ε α 2 = ε x + ε y 2 + ε x − ε y 2 cos 2 α 2 + γ x y 2 sin 2 α 2 ε α 3 = ε x + ε y 2 + ε x − ε y 2 cos 2 α 3 + γ x y 2 sin 2 α 3 } \left. \begin{array}{l} \varepsilon_{\alpha_1} = \frac{\varepsilon_x + \varepsilon_y}{2} + \frac{\varepsilon_x - \varepsilon_y}{2} \cos 2\alpha_1 + \frac{\gamma_{xy}}{2} \sin 2\alpha_1 \\ \varepsilon_{\alpha_2} = \frac{\varepsilon_x + \varepsilon_y}{2} + \frac{\varepsilon_x - \varepsilon_y}{2} \cos 2\alpha_2 + \frac{\gamma_{xy}}{2} \sin 2\alpha_2 \\ \varepsilon_{\alpha_3} = \frac{\varepsilon_x + \varepsilon_y}{2} + \frac{\varepsilon_x - \varepsilon_y}{2} \cos 2\alpha_3 + \frac{\gamma_{xy}}{2} \sin 2\alpha_3 \end{array} \right\} εα1=2εx+εy+2εx−εycos2α1+2γxysin2α1εα2=2εx+εy+2εx−εycos2α2+2γxysin2α2εα3=2εx+εy+2εx−εycos2α3+2γxysin2α3⎭ ⎬ ⎫
将 ε x + ε y 2 \frac{\varepsilon_x+\varepsilon_y}{2} 2εx+εy、 ε x − ε y 2 \frac{\varepsilon_x-\varepsilon_y}{2} 2εx−εy和 γ x y \gamma_{xy} γxy视为变量,设 $ A = \frac{\varepsilon_x + \varepsilon_y}{2} , , ,B = \frac{\varepsilon_x - \varepsilon_y}{2} , , ,C = \frac{\gamma_{xy}}{2}$,原方程组化为:
{ ε α 1 = A + B cos 2 α 1 + C sin 2 α 1 ε α 2 = A + B cos 2 α 2 + C sin 2 α 2 ε α 3 = A + B cos 2 α 3 + C sin 2 α 3 \begin{cases} \varepsilon_{\alpha_1} = A + B \cos 2\alpha_1 + C \sin 2\alpha_1 \\ \varepsilon_{\alpha_2} = A + B \cos 2\alpha_2 + C \sin 2\alpha_2 \\ \varepsilon_{\alpha_3} = A + B \cos 2\alpha_3 + C \sin 2\alpha_3 \end{cases} ⎩ ⎨ ⎧εα1=A+Bcos2α1+Csin2α1εα2=A+Bcos2α2+Csin2α2εα3=A+Bcos2α3+Csin2α3
消去 $ A$ 后利用三角恒等式化简,通过线性方程组解得:
B = ε α 2 − ε α 1 2 sin ( α 2 − α 1 ) cos ( α 1 + α 3 ) − ε α 3 − ε α 1 2 sin ( α 3 − α 1 ) cos ( α 1 + α 2 ) sin ( α 3 − α 2 ) , C = ε α 3 − ε α 1 2 sin ( α 3 − α 1 ) sin ( α 1 + α 2 ) − ε α 2 − ε α 1 2 sin ( α 2 − α 1 ) sin ( α 1 + α 3 ) sin ( α 3 − α 2 ) , A = ε α 1 − B cos 2 α 1 − C sin 2 α 1 . \begin{align*} B &= \frac{\frac{\varepsilon_{\alpha_2}-\varepsilon_{\alpha_1}}{2\sin(\alpha_2-\alpha_1)}\cos(\alpha_1+\alpha_3) - \frac{\varepsilon_{\alpha_3}-\varepsilon_{\alpha_1}}{2\sin(\alpha_3-\alpha_1)}\cos(\alpha_1+\alpha_2)}{\sin(\alpha_3-\alpha_2)}, \\ C &= \frac{\frac{\varepsilon_{\alpha_3}-\varepsilon_{\alpha_1}}{2\sin(\alpha_3-\alpha_1)}\sin(\alpha_1+\alpha_2) - \frac{\varepsilon_{\alpha_2}-\varepsilon_{\alpha_1}}{2\sin(\alpha_2-\alpha_1)}\sin(\alpha_1+\alpha_3)}{\sin(\alpha_3-\alpha_2)}, \\ A &= \varepsilon_{\alpha_1} - B\cos2\alpha_1 - C\sin2\alpha_1. \end{align*} BCA=sin(α3−α2)2sin(α2−α1)εα2−εα1cos(α1+α3)−2sin(α3−α1)εα3−εα1cos(α1+α2),=sin(α3−α2)2sin(α3−α1)εα3−εα1sin(α1+α2)−2sin(α2−α1)εα2−εα1sin(α1+α3),=εα1−Bcos2α1−Csin2α1.
还原变量得:
ε x = A + B , ε y = A − B , γ x y = 2 C . \varepsilon_x = A+B, \quad \varepsilon_y = A-B, \quad \gamma_{xy} = 2C. εx=A+B,εy=A−B,γxy=2C.
由此可以带入应变圆得到上述题目各个表达式。
第四题
使用广义胡克定律证明弹性常数之间的关系。 G = E 2 ( 1 + μ ) G=\frac{E}{2(1+\mu)} G=2(1+μ)E K = E 3 ( 1 − 2 μ ) K=\frac{E}{3(1-2\mu)} K=3(1−2μ)E
证明
广义胡克定律
{ ε x = 1 E [ σ x − μ ( σ y + σ z ) ] ε x = 1 E [ σ x − μ ( σ y + σ z ) ] ε x = 1 E [ σ x − μ ( σ y + σ z ) ] γ x y = τ x y G γ y z = τ y z G γ z x = τ z x G \begin{cases} \varepsilon_{x}=\frac{1}{E}[\sigma_x-\mu(\sigma_y+\sigma_{z})]\\ \varepsilon_{x}=\frac{1}{E}[\sigma_x-\mu(\sigma_y+\sigma_{z})]\\ \varepsilon_{x}=\frac{1}{E}[\sigma_x-\mu(\sigma_y+\sigma_{z})]\\ \gamma_{xy}=\frac{\tau_{xy}}{G}\\ \gamma_{yz}=\frac{\tau_{yz}}{G}\\ \gamma_{zx}=\frac{\tau_{zx}}{G} \end{cases} ⎩ ⎨ ⎧εx=E1[σx−μ(σy+σz)]εx=E1[σx−μ(σy+σz)]εx=E1[σx−μ(σy+σz)]γxy=Gτxyγyz=Gτyzγzx=Gτzx
(a)
首先,证明 G = E 2 ( 1 + μ ) \boxed{G=\frac{E}{2(1+\mu)}} G=2(1+μ)E
在纯剪切状态下:
σ x = σ y = σ z = 0 , τ x y ≠ 0 \sigma_x = \sigma_y = \sigma_z = 0, \quad \tau_{xy} \neq 0 σx=σy=σz=0,τxy=0
由剪切本构方程:
γ x y = τ x y G ( 1 ) \gamma_{xy} = \frac{\tau_{xy}}{G} \quad (1) γxy=Gτxy(1)
旋转坐标系 4 5 ∘ 45^\circ 45∘ 后,主应力为:
σ 1 = τ x y , σ 2 = − τ x y \sigma_{1} = \tau_{xy}, \quad \sigma_{2} = -\tau_{xy} σ1=τxy,σ2=−τxy
对应正应变为:
ε 1 = τ x y E ( 1 + μ ) , ε 2 = − τ x y E ( 1 + μ ) \varepsilon_1 = \frac{\tau_{xy}}{E}(1+\mu), \quad \varepsilon_2 = -\frac{\tau_{xy}}{E}(1+\mu) ε1=Eτxy(1+μ),ε2=−Eτxy(1+μ)
几何关系:
γ x y = ε 1 − ε 2 = 2 τ x y ( 1 + μ ) E ( 2 ) \gamma_{xy} = \varepsilon_1 - \varepsilon_2 = \frac{2\tau_{xy}(1+\mu)}{E} \quad (2) γxy=ε1−ε2=E2τxy(1+μ)(2)
联立 ( 1 ) (1) (1) 和 ( 2 ) (2) (2):
τ x y G = 2 τ x y ( 1 + μ ) E ⟹ G = E 2 ( 1 + μ ) \frac{\tau_{xy}}{G} = \frac{2\tau_{xy}(1+\mu)}{E} \implies G = \frac{E}{2(1+\mu)} Gτxy=E2τxy(1+μ)⟹G=2(1+μ)E
(b)
其次,证明 K = E 3 ( 1 − 2 μ ) \boxed{K=\frac{E}{3(1-2\mu)}} K=3(1−2μ)E
对于六面体其变形前的体积
V = d x d y d z V=\text{d}x\text{d}y\text{d}z V=dxdydz
变形后体积
V 1 = ( 1 + ε 1 + ε 2 + ε 3 ) V V_1=(1+\varepsilon_1+\varepsilon_2+\varepsilon_3)V V1=(1+ε1+ε2+ε3)V
体应变
θ = ε 1 + ε 2 + ε 3 = 1 − 2 μ E ( σ 1 + σ 2 + σ 3 ) \theta=\varepsilon_1+\varepsilon_2+\varepsilon_3=\frac{1-2\mu}{E}(\sigma_1+\sigma_2+\sigma_3) θ=ε1+ε2+ε3=E1−2μ(σ1+σ2+σ3)
对比
θ = σ m K \theta=\frac{\sigma_m}{K} θ=Kσm
其中, σ m = σ 1 + σ 2 + σ 3 3 \sigma_m=\frac{\sigma_1+\sigma_2+\sigma_3}{3} σm=3σ1+σ2+σ3
得到
K = E 3 ( 1 − 2 μ ) K=\frac{E}{3(1-2\mu)} K=3(1−2μ)E
相关文章:

随笔:hhhhh
第一题 ∫ − ∞ ∞ x e x − e x d x ∫ 0 ∞ ln t ⋅ e ln t − t ⋅ 1 t d t ∫ 0 ∞ ln t ⋅ e − t ⋅ 1 t ⋅ t d t ∫ 0 ∞ ln t ⋅ e − t d t ψ ( 1 ) − γ \begin{align*} \int_{-\infty}^{\infty}xe^{x-e^x}\text{d}x&\int_{0}^{\infty}…...

PR-2021
推荐深蓝学院的《深度神经网络加速:cuDNN 与 TensorRT》,课程面向就业,细致讲解CUDA运算的理论支撑与实践,学完可以系统化掌握CUDA基础编程知识以及TensorRT实战,并且能够利用GPU开发高性能、高并发的软件系统…...
和 Anaconda 的不同)
CMD(Command Prompt)和 Anaconda 的不同
CMD(Command Prompt)和 Anaconda 是两种不同的工具,它们在功能和用途上有明显的区别: CMD(Command Prompt) 定义:CMD 是 Windows 操作系统自带的一个命令行界面工具。 主要用途: 文件…...
)
软考 系统架构设计师系列知识点之杂项集萃(60)
接前一篇文章:软考 系统架构设计师系列知识点之杂项集萃(59) 第97题 在面向对象设计中,()可以实现界面控制、外部接口和环境隔离。()作为完成用例业务的责任承担者,协调…...

如何备考GRE?
1.引言 GRE和雅思不太相同,首先GRE是美国人的考试,思维方式和很多细节和英系雅思不一样。所以底层逻辑上我觉得有点区别。 难度方面,我感觉GRE不容易考低分,但考高分较难。雅思就不一样了不仅上限难突破,下限还容易6…...

Linux复习笔记(六)shell编程
遇到的问题,都有解决方案,希望我的博客能为你提供一点帮助。 三、shell编程简明教程 一、Shell基础概念 1. Shell的作用 是用户与Linux内核交互的桥梁,既是命令解释器,也是一种脚本语言。运行机制:用户输入…...

Unity 拖尾烟尘效果及参数展示
亮点:在移动特效过后 ,粒子会顺着惯性继续向前移动一小段距离。 以unity-URP管线为例,下图是Particle System参数分享: Start Color参数: UnityEditor.GradientWrapperJSON:{"gradient":{"serialized…...
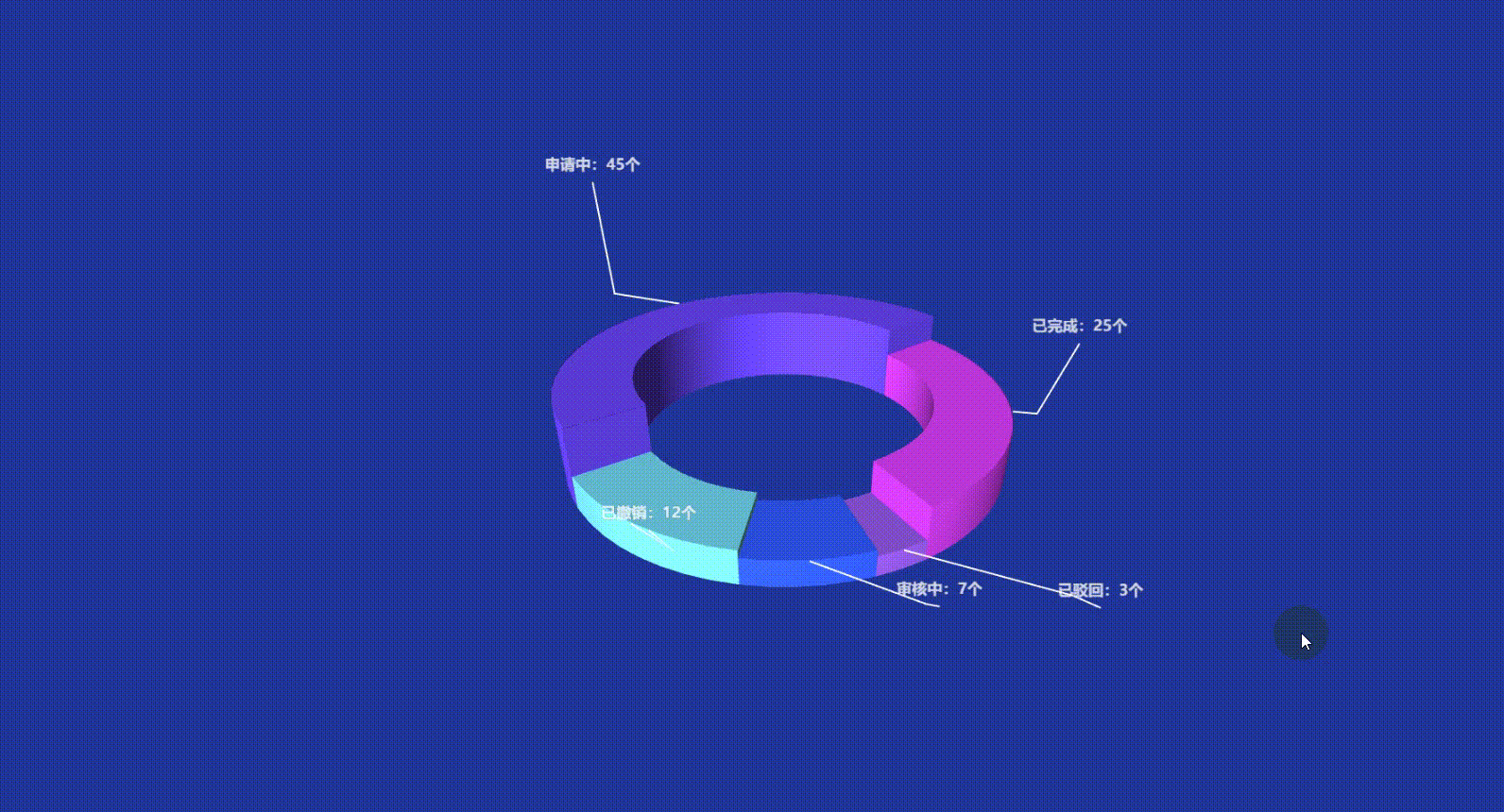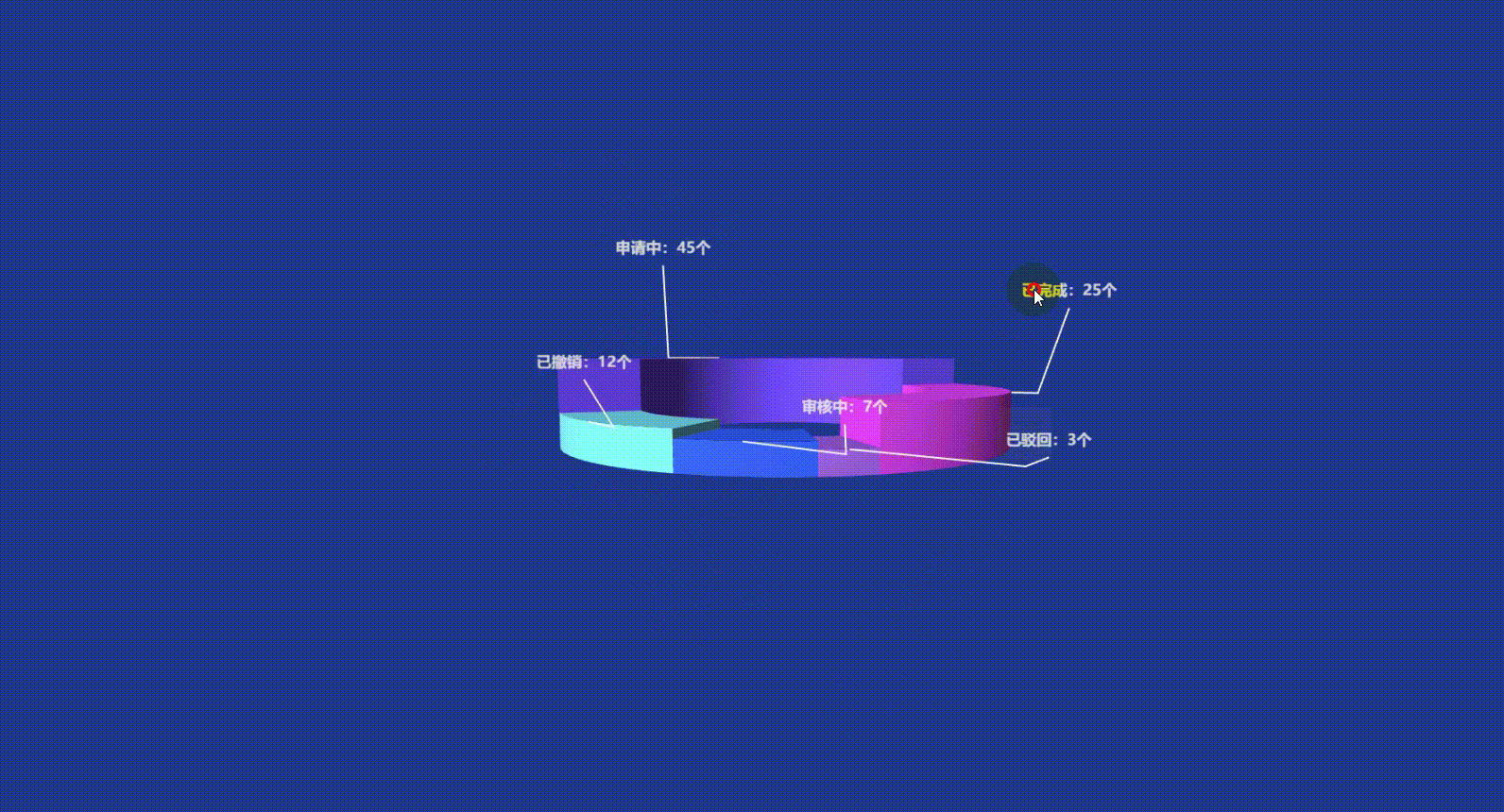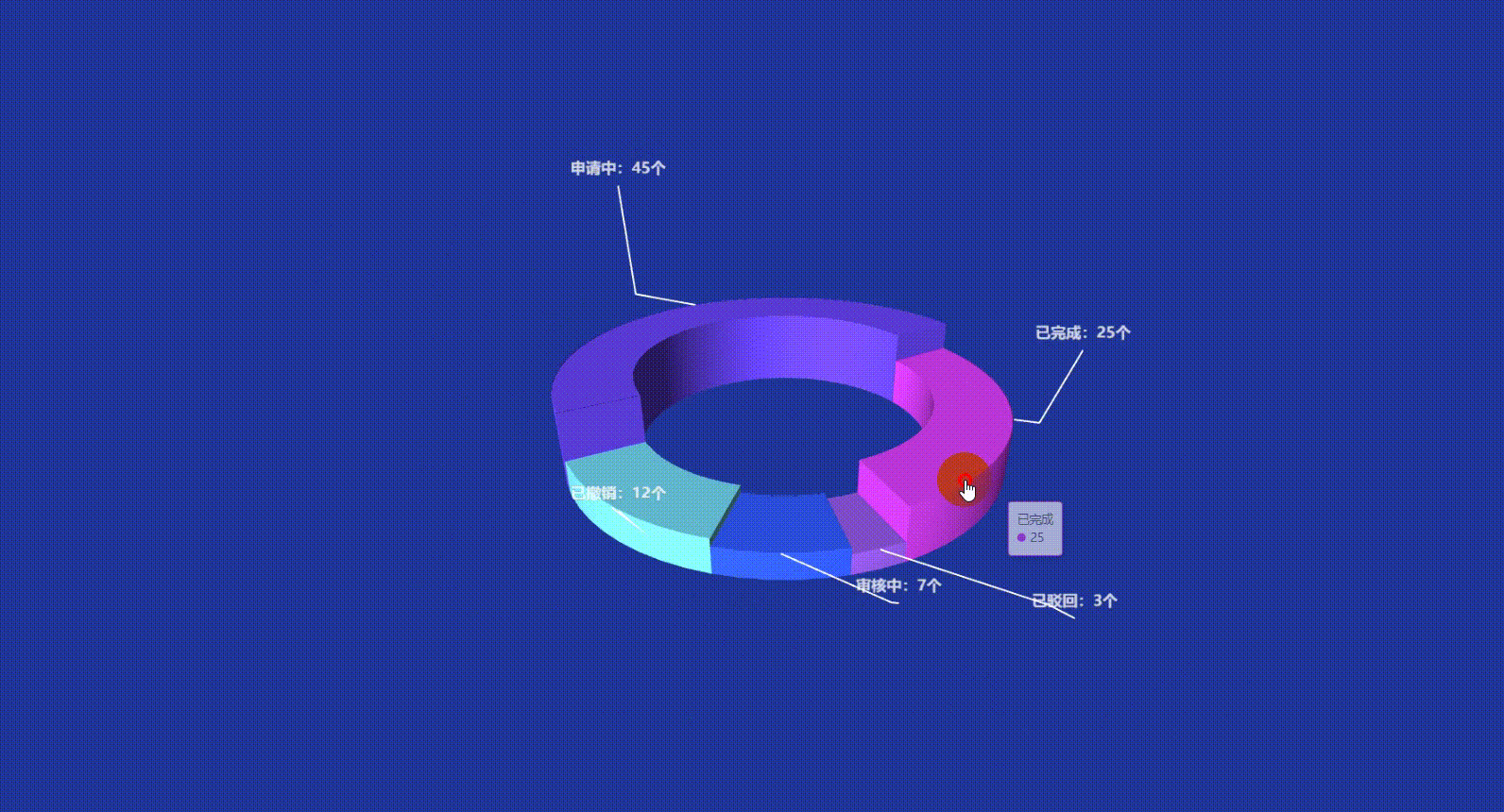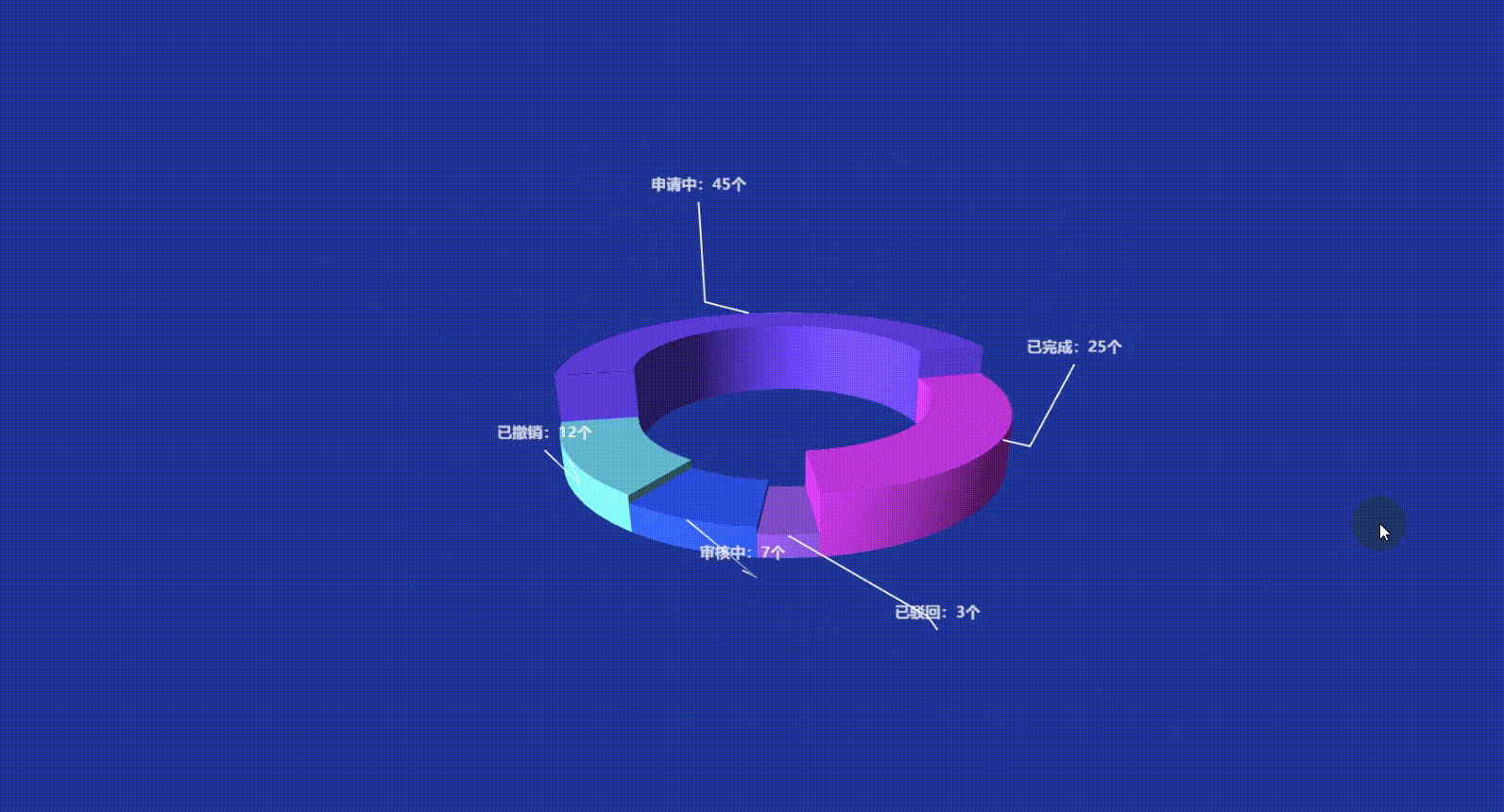
Vue3 Echarts 3D饼图(3D环形图)实现讲解附带源码
文章目录 前言一、准备工作1. 所需工具2. 引入依赖方式一:CDN 快速引入方式二:npm 本地安装(推荐) 二、实现原理解析三、echarts-gl 3D插件 使用回顾grid3D 常用通用属性:series 常用通用属性:surface&…...

Kafka快速安装与使用
引言 这篇文章是一篇Ubuntu(Linux)环境下的Kafka安装与使用教程,通过本文,你可以非常快速搭建一个kafka的小单元进行日常开发与调测。 安装步骤 下载与解压安装 首先我们需要下载一下Kafka,这里笔者采用wget指令: wget https:…...

Java EE初阶——wait 和 notify
1. 线程饥饿 线程饥饿是指一个或多个线程因长期无法获取所需资源(如锁,CPU时间等)而持续处于等待状态,导致其任务无法推进的现象。 典型场景 优先级抢占: 在支持线程优先级的系统中,高优先级线程可能持续…...

RPA vs. 传统浏览器自动化:效率与灵活性的终极较量
1. 引言 在数字化转型的大潮下,企业和开发者对浏览器自动化的需求日益增长。无论是网页数据抓取、自动化测试,还是用户行为模拟,浏览器自动化已经成为提升效率的关键工具。然而,面对越来越严格的反自动化检测、复杂的 Web 结构和…...

Flask框架深度解析:蓝图、上下文机制与Jinja2模板引擎实战
Flask作为Python最流行的轻量级Web框架之一,以其简洁、灵活和高度可扩展的特性赢得了广大开发者的青睐。本文将深入探讨Flask框架的三大核心特性:蓝图(Blueprint)模块化开发、上下文(Context)管理机制以及Jinja2模板引擎的高级用法。无论你是Flask初学者…...

docker 快速部署若依项目
1、首先创建一个自定义网络,作用是使连接到该网络的容器能够通过容器名称进行通信,无需使用复杂的IP地址配置,方便了容器化应用中各个服务之间的交互。 sudo docker network create ruoyi 2、创建一个文件夹,创建compose.yml文件…...

polarctf-web-[rce1]
考点: (1)RCE(exec函数) (2)空格绕过 (3)执行函数(exec函数) (4)闭合(ping命令闭合) 题目来源:Polarctf-web-[rce1] 解题: 这段代码实现了一个简单的 Ping 测试工具,用户可以通过表单提交一个 IP 地址,服务器会执…...

数据备份与恢复方案
数据备份与恢复方案 一.背景 为确保公司信息安全,防止关键数据丢失,应对突发事件,特制定全面的数据备份与恢复方案。该方案将对公司的各类文件资料进行分级管理,并针对不同级别的数据设定相应的备份策略和恢复流程。 二…...

Redis+Caffeine构造多级缓存
一、背景 项目中对性能要求极高,因此使用多级缓存,最终方案决定是RedisCaffeine。其中Redis作为二级缓存,Caffeine作为一级本地缓存。 二、Caffeine简单介绍 Caffeine是一款基于Java 8的高性能、灵活的本地缓存库。它提供了近乎最佳的命中…...

docker(四)使用篇二:docker 镜像
在上一章中,我们介绍了 docker 镜像仓库,本文就来介绍 docker 镜像。 一、什么是镜像 docker 镜像本质上是一个 read-only 只读文件, 这个文件包含了文件系统、源码、库文件、依赖、工具等一些运行 application 所必须的文件。 我们可以把…...

ms-swift 代码推理数据集
目前想要对SFT微调后的模型进行测试,看官方文档ms-swift中有eval的教程,但是从介绍来看,eval使用的是modelscope的评测内容。 评测 SWIFT支持了eval(评测)能力,用于对原始模型和训练后的模型给出标准化…...

AXI4总线协议 ------ AXI_LITE协议
一、AXI 相关知识介绍 https://download.csdn.net/download/mvpkuku/90841873 AXI_LITE 选出部分重点,详细文档见上面链接。 1.AXI4 协议类型 2.握手机制 二、AXI_LITE 协议的实现 1. AXI_LITE 通道及各通道端口功能介绍 2.实现思路及框架 2.1 总体框架 2.2 …...

DATE_FORMAT可以接收date类型,也可以接收String类型!
DATE_FORMAT 是 SQL 函数,主要用于将日期/时间类型的字段按照指定格式转换成字符串。在 MyBatis 的 XML 动态 SQL 中,你看到的这段代码是为了比较数据库中的日期字段和传入参数的日期值,但会忽略时间部分,只比较年月日。 代码解释…...

Ubuntu24.04 安装 5080显卡驱动以及cuda
前言 之前使用Ubuntu22.04版本一直报错,然后换了24.04版本才能正常安装 一. 配置基础环境 Linux系统进行环境开发环境配置-CSDN博客 二. 安装显卡驱动 1.安装驱动 按以下步骤来: sudo apt update && sudo apt upgrade -y#下载最新内核并安装 sudo add…...

华三H3C交换机配置NTP时钟步骤 示例
现场1台H3C 5110交换机 版本:Comware Software, Version 5.20.99, Release 1105 当前没有指定NTP, <H3C-5110>dis ntp-service status Clock status: unsynchronizedClock stratum: 16Reference clock ID: noneNominal frequency: 100.0000 HzAc…...
)
RKNN开发环境搭建(ubuntu22.04)
以下情况在RV1106G3的平台上验证正常。 1、conda安装 1)conda --version//确认是否安装 2)创建一个安装目录,进行下一步 3)wget https://mirrors.tuna.tsinghua.edu.cn/anaconda/miniconda/Miniconda3-4.6.14-Linux-x…...

matlab多项式
1. 多项式表示 多项式用行向量表示,按降幂排列系数。例如,多项式 3x22x1 表示为 [3 2 1]。 2. 创建多项式 直接输入系数:如 p [1 -3 3 -1] 表示 x3−3x23x−1。由根创建:使用 poly 函数。例如,根为 [1, 1, 1]&…...
?)
Sprnig MVC 如何统一异常处理 (Exception Handling)?
主要有以下几种方式来实现统一异常处理,其中 ControllerAdvice (或 RestControllerAdvice) 结合 ExceptionHandler 是最常用的方式。 1. ExceptionHandler 注解 作用: 用于标记一个方法,该方法将处理在同一个 Controller 类中抛出的特定类型…...

SpringAI-RC1正式发布:移除千帆大模型!
续 Spring AI M8 版本之后(5.1 发布),前几日 Spring AI 悄悄的发布了最新版 Spring AI 1.0.0 RC1(5.13 发布),此版本也将是 GA(Generally Available,正式版)发布前的最后…...

操作系统之进程和线程听课笔记
计算机的上电运行就是构建进程树,进程调度就是在进程树节点进程进行切换 进程间通信的好处 经典模型 生产者和消费者 进程和线程的区别 线程引入带来的问题线程的优势 由于unix70年代产生,90年代有线程,当时数据库系统操作需要线程,操作系统没有来得及重造,出现了用户态线…...

【vue】封装接口,全局字典,表格表头及使用
一、封装接口(API请求) 1. 创建axios实例 // src/utils/request.js import axios from axiosconst service axios.create({baseURL: process.env.VUE_APP_BASE_API,timeout: 10000 })// 请求拦截器 service.interceptors.request.use(config > {co…...

深入解析ZAB协议:ZooKeeper的分布式一致性核心
引言 在分布式系统中,如何高效、可靠地实现多节点间的数据一致性是核心挑战之一。ZAB协议(ZooKeeper Atomic Broadcast)作为 ZooKeeper的核心算法,被广泛应用于分布式协调服务(如Kafka、HBase、Dubbo等)。…...

COMSOL随机参数化表面流体流动模拟
基于粗糙度表面的裂隙流研究对于理解地下水的流动、污染物传输以及与之相关的地质灾害(如滑坡)等方面具有重要意义。本研究通过蒙特卡洛方法生成随机表面形貌,并利用COMSOL Multiphysics对随机参数化表面的微尺度流体流动进行模拟。 参数化…...
