【排序算法】典型排序算法 Java实现
以下是典型的排序算法分类及对应的 Java 实现,包含时间复杂度、稳定性说明和核心代码示例:
一、比较类排序(通过元素比较)
1. 交换排序
① 冒泡排序
时间复杂度:O(n²)(优化后最优O(n))
稳定性:稳定
public static void bubbleSort(int[] arr) {boolean swapped;for (int i = 0; i < arr.length - 1; i++) {swapped = false;for (int j = 0; j < arr.length - i - 1; j++) {if (arr[j] > arr[j + 1]) {int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;swapped = true;}}if (!swapped) break; // 提前终止优化}
}
② 快速排序
时间复杂度:平均 O(n log n),最差 O(n²)
稳定性:不稳定
public static void quickSort(int[] arr, int low, int high) {if (low < high) {int pivot = partition(arr, low, high);quickSort(arr, low, pivot - 1);quickSort(arr, pivot + 1, high);}
}private static int partition(int[] arr, int low, int high) {int pivot = arr[high]; // 选择末尾为基准int i = low - 1;for (int j = low; j < high; j++) {if (arr[j] < pivot) {i++;int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}}int temp = arr[i + 1];arr[i + 1] = arr[high];arr[high] = temp;return i + 1;
}
2. 插入排序
① 直接插入排序
时间复杂度:O(n²)(最优O(n))
稳定性:稳定
public static void insertionSort(int[] arr) {for (int i = 1; i < arr.length; i++) {int key = arr[i];int j = i - 1;while (j >= 0 && arr[j] > key) {arr[j + 1] = arr[j];j--;}arr[j + 1] = key;}
}
3. 选择排序
① 简单选择排序
时间复杂度:O(n²)
稳定性:不稳定
public static void selectionSort(int[] arr) {for (int i = 0; i < arr.length - 1; i++) {int minIdx = i;for (int j = i + 1; j < arr.length; j++) {if (arr[j] < arr[minIdx]) {minIdx = j;}}int temp = arr[minIdx];arr[minIdx] = arr[i];arr[i] = temp;}
}
4. 归并排序
时间复杂度:O(n log n)
稳定性:稳定
public static void mergeSort(int[] arr, int left, int right) {if (left < right) {int mid = left + (right - left) / 2;mergeSort(arr, left, mid);mergeSort(arr, mid + 1, right);merge(arr, left, mid, right);}
}private static void merge(int[] arr, int left, int mid, int right) {int[] temp = new int[right - left + 1];int i = left, j = mid + 1, k = 0;while (i <= mid && j <= right) {temp[k++] = arr[i] <= arr[j] ? arr[i++] : arr[j++];}while (i <= mid) temp[k++] = arr[i++];while (j <= right) temp[k++] = arr[j++];System.arraycopy(temp, 0, arr, left, temp.length);
}
5. 堆排序
时间复杂度:O(n log n)
稳定性:不稳定
public static void heapSort(int[] arr) {// 构建最大堆for (int i = arr.length / 2 - 1; i >= 0; i--) {heapify(arr, arr.length, i);}// 逐步提取堆顶元素for (int i = arr.length - 1; i > 0; i--) {int temp = arr[0];arr[0] = arr[i];arr[i] = temp;heapify(arr, i, 0);}
}private static void heapify(int[] arr, int n, int i) {int largest = i;int left = 2 * i + 1;int right = 2 * i + 2;if (left < n && arr[left] > arr[largest]) largest = left;if (right < n && arr[right] > arr[largest]) largest = right;if (largest != i) {int swap = arr[i];arr[i] = arr[largest];arr[largest] = swap;heapify(arr, n, largest);}
}
二、非比较类排序(利用数值特征)
1. 计数排序
时间复杂度:O(n + k)(k 为数据范围)
稳定性:稳定
适用场景:整数且范围较小
public static void countingSort(int[] arr) {int max = Arrays.stream(arr).max().getAsInt();int[] count = new int[max + 1];for (int num : arr) count[num]++;int idx = 0;for (int i = 0; i <= max; i++) {while (count[i]-- > 0) {arr[idx++] = i;}}
}
2. 基数排序
时间复杂度:O(nk)(k 为最大位数)
稳定性:稳定
public static void radixSort(int[] arr) {int max = Arrays.stream(arr).max().getAsInt();for (int exp = 1; max / exp > 0; exp *= 10) {countSortByDigit(arr, exp);}
}private static void countSortByDigit(int[] arr, int exp) {int[] output = new int[arr.length];int[] count = new int[10];for (int num : arr) count[(num / exp) % 10]++;for (int i = 1; i < 10; i++) count[i] += count[i - 1];for (int i = arr.length - 1; i >= 0; i--) {output[count[(arr[i] / exp) % 10] - 1] = arr[i];count[(arr[i] / exp) % 10]--;}System.arraycopy(output, 0, arr, 0, arr.length);
}
三、总结与选择建议
| 算法 | 平均时间复杂度 | 空间复杂度 | 稳定性 | 适用场景 |
|---|---|---|---|---|
| 冒泡排序 | O(n²) | O(1) | 稳定 | 小数据、教学演示 |
| 快速排序 | O(n log n) | O(log n) | 不稳定 | 通用场景(优化后高效) |
| 归并排序 | O(n log n) | O(n) | 稳定 | 大数据、稳定排序需求 |
| 堆排序 | O(n log n) | O(1) | 不稳定 | 原地排序、内存敏感场景 |
| 计数排序 | O(n + k) | O(k) | 稳定 | 整数且数值范围小 |
| 基数排序 | O(nk) | O(n + k) | 稳定 | 多位数整数(如身份证号) |
实际建议:
- 小规模数据:插入排序或冒泡排序(简单实现)。
- 通用场景:优先选择快速排序(需优化基准选择)。
- 稳定排序需求:归并排序或基数排序。
- 特定数值特征:计数排序/基数排序效率碾压比较排序。
相关文章:

【排序算法】典型排序算法 Java实现
以下是典型的排序算法分类及对应的 Java 实现,包含时间复杂度、稳定性说明和核心代码示例: 一、比较类排序(通过元素比较) 1. 交换排序 ① 冒泡排序 时间复杂度:O(n)(优化后最优O(n)) 稳定性&…...

node.js如何实现双 Token + Cookie 存储 + 无感刷新机制
node.js如何实现双 Token Cookie 存储 无感刷新机制 为什么要实施双token机制? 优点描述安全性Access Token 短期有效,降低泄露风险;Refresh Token 权限受限,仅用于获取新 Token用户体验用户无需频繁重新登录,Toke…...

[DS]使用 Python 库中自带的数据集来实现上述 50 个数据分析和数据可视化程序的示例代码
使用 Python 库中自带的数据集来实现上述 50 个数据分析和数据可视化程序的示例代码 摘要:由于 sample_data.csv 是一个占位符文件,用于代表任意数据集,我将使用 Python 库中自带的数据集来实现上述 50 个数据分析和数据可视化程序的示例代码…...

探索智能仓颉
探索智能仓颉:Cangjie Magic体验有感 一、引言 在人工智能和智能体开发领域,新的技术和框架不断涌现,推动着行业的快速发展。2025年3月,仓颉社区开源了Cangjie Magic,这是一个基于仓颉编程语言原生构建的LLM Agent开…...

Ubuntu 上开启 SSH 服务、禁用密码登录并仅允许密钥认证
1. 安装 OpenSSH 服务 如果尚未安装 SSH 服务,运行以下命令: sudo apt update sudo apt install openssh-server2. 启动 SSH 服务并设置开机自启 sudo systemctl start ssh sudo systemctl enable ssh3. 生成 SSH 密钥对(本地机器…...

LLMs之Qwen:《Qwen3 Technical Report》翻译与解读
LLMs之Qwen:《Qwen3 Technical Report》翻译与解读 导读:Qwen3是Qwen系列最新的大型语言模型,它通过集成思考和非思考模式、引入思考调度机制、扩展多语言支持以及采用强到弱的知识等创新技术,在性能、效率和多语言能力方面都取得…...

springboot3 configuration
1 多数据库配置 github: https://github.com/baomidou/dynamic-datasource 使用DS()注解来切换数据库 详情介绍:https://www.kancloud.cn/tracy5546/dynamic-datasource/2264611 注意:DS 可以注解在方法上或类上,同时存在就近原则 方法上注…...
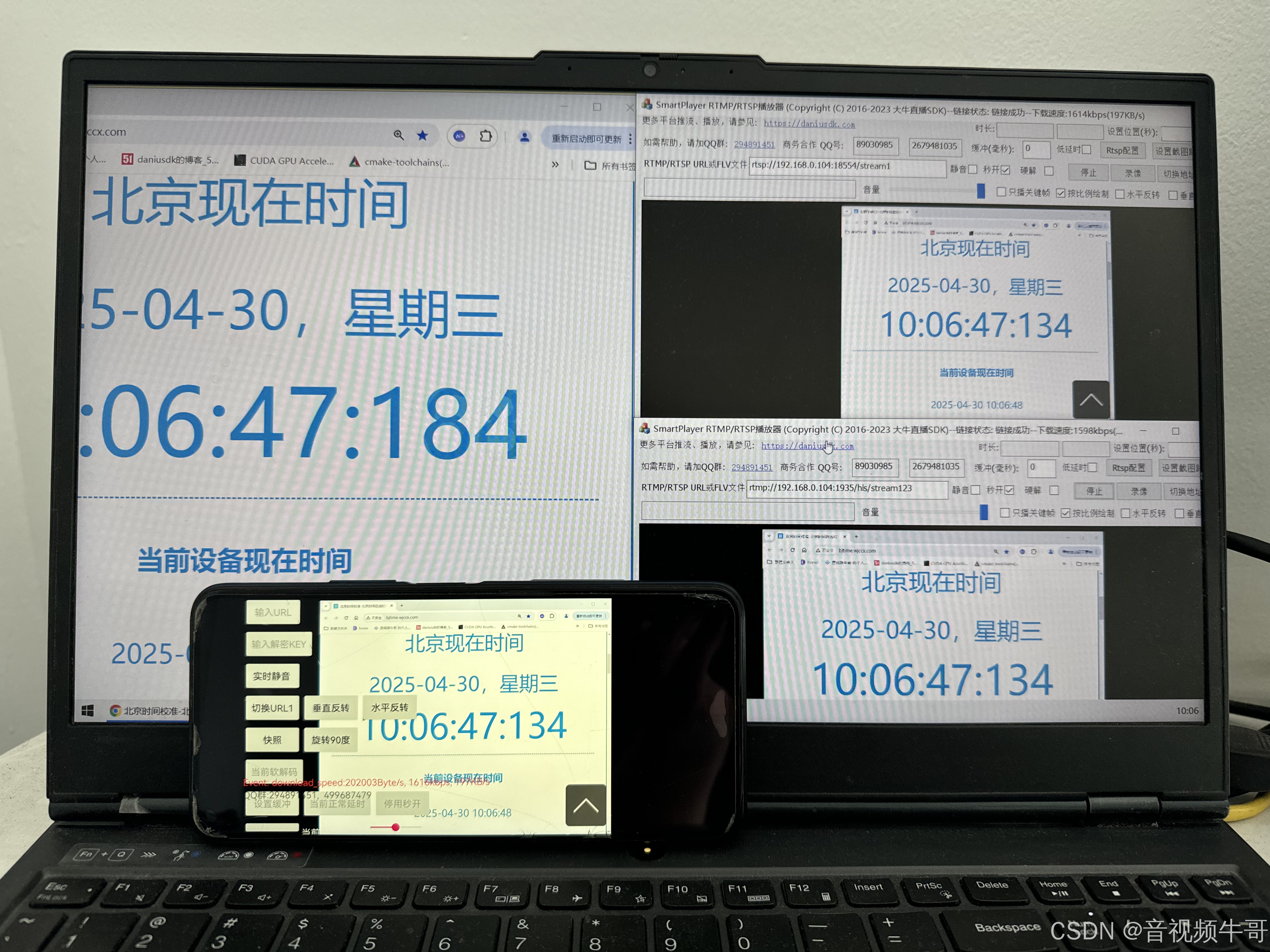
从工程实践角度分析H.264与H.265的技术差异
作为音视频从业者,我们时刻关注着视频编解码技术的最新发展。RTMP推流、轻量级RTSP服务、RTMP播放、RTSP播放等模块是大牛直播SDK的核心功能,在这些模块的实现过程中,H.264和H.265两种视频编码格式的应用实践差异是我们技术团队不断深入思考的…...

如何设计一个高性能的短链设计
1.什么是短链 短链接(Short URL) 是通过算法将长 URL 压缩成简短字符串的技术方案。例如将 https://flowus.cn/veal/share/3306b991-e1e3-4c92-9105-95abf086ae4e 缩短为 https://sourl.cn/aY95qu,用户点击短链时会自动重定向到原始长链接。其…...
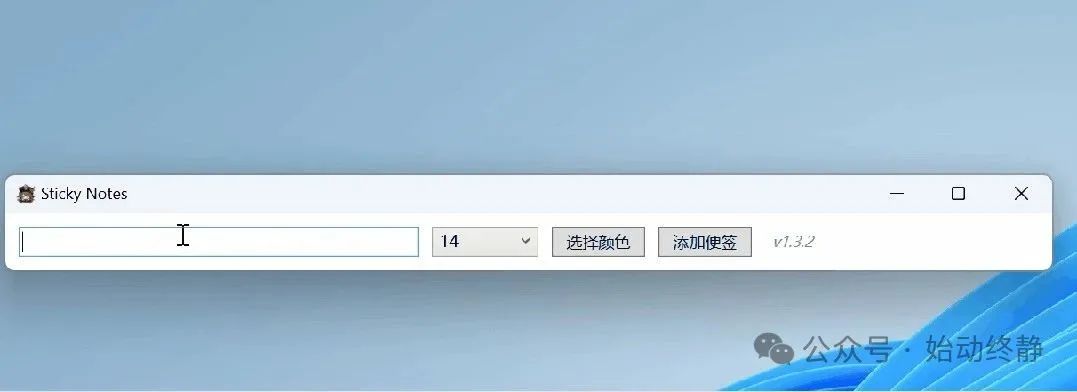
提升工作效率的可视化笔记应用程序
StickyNotes桌面便签软件介绍 StickyNotes是一款极为简洁的桌面便签应用程序,让您能够快速记录想法、待办事项或其他重要信息。这款工具操作极其直观,只需输入文字内容,选择合适的字体大小和颜色,然后点击添加按钮即可创建个性化…...

11|省下钱买显卡,如何利用开源模型节约成本?
不知道课程上到这里,你账户里免费的5美元的额度还剩下多少了?如果你尝试着完成我给的几个数据集里的思考题,相信这个额度应该是不太够用的。而ChatCompletion的接口,又需要传入大量的上下文信息,实际消耗的Token数量其…...

GDB调试工具详解
GDB调试工具详解 一、基本概念 调试信息 编译时需添加 -g 选项(如 gcc -g -o program program.c),生成包含变量名、函数名、行号等调试信息的可执行文件。断点(Breakpoint) 程序执行到指定位置(函数、行号…...

机器学习圣经PRML作者Bishop20年后新作中文版出版!
机器学习圣经PRML作者Bishop20年后新书《深度学习:基础与概念》出版。作者克里斯托弗M. 毕晓普(Christopher M. Bishop)微软公司技术研究员、微软研究 院 科学智 能 中 心(Microsoft Research AI4Science)负责人。剑桥…...

Armadillo C++ 线性代数库介绍与使用
文章目录 Armadillo C 线性代数库介绍与使用主要特点安装Linux (Ubuntu/Debian)macOS (使用 Homebrew)Windows (使用 vcpkg) 基本使用包含头文件矩阵创建与初始化基本运算矩阵分解统计运算保存和加载数据 性能优化建议示例程序与 MATLAB 语法对比 使用Armadillo函数库的稀疏矩阵…...

吴恩达机器学习笔记:逻辑回归3
3.判定边界 现在说下决策边界(decision boundary)的概念。这个概念能更好地帮助我们理解逻辑回归的假设函数在计算什么。 在逻辑回归中,我们预测: 当ℎθ (x) > 0.5时,预测 y 1。 当ℎθ (x) < 0.5时,预测 y 0 。 根据…...

大模型知识
############################################################## 一、vllm大模型测试参数和原理 tempreature top_p top_k ############################################################## tempreature top_p top_k 作用:总体是控制模型的发散程度、多样…...

C/C++ 结构体:. 与 -> 的区别与用法及其STM32中的使用
目录 引言 一、深入理解 C/C 结构体:. 与 -> 的区别与用法 1. .(点运算符)详解2. ->(箭头运算符)详解3. . 与 -> 的等价与转换4. 常见错误与调试技巧5. C 特性与运算符重载6. 实战案例:链表与智能…...

docker中使用openresty
1.为什么要使用openresty 我这边是因为要使用1Panel,第一个最大的原因,就是图方便,比较可以一键安装。但以前一直都是直接安装nginx。所以需要一个过度。 2.如何查看openResty使用了nginx哪个版本 /usr/local/openresty/nginx/sbin/nginx …...

Jetpack Compose 中更新应用语言
在 Jetpack Compose 应用中更新语言需要结合传统的 Android 语言配置方法和 Compose 的重组机制。以下是完整的实现方案: 1. 创建语言管理类 object LocaleManager {private var currentLocale: Locale Locale.getDefault()fun setLocale(context: Context, local…...

Java 中的 super 关键字
个人总结: 1.子类构造方法中没有显式使用super,Java 也会默认调用父类的无参构造方法 2.当父类中没有无参构造方法,只有有参构造方法时,子类构造方法就必须显式地使用super来调用父类的有参构造方法。 3.如果父类没有定义任何构造…...

CMake基础:CMakeLists.txt 文件结构和语法
目录 1.CMakeLists.txt基本结构 2.核心语法规则 3.关键命令详解 4.常用预定义变量 5.变量和缓存 6.变量作用域与传递 7.注意事项 1.CMakeLists.txt基本结构 CMakeLists.txt 是 CMake 构建系统的核心配置文件,采用命令式语法组织项目结构和编译流程。主要用于…...

PCM音频数据的编解码
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、pandas是什么?二、使用步骤 1.引入库2.读入数据 总结 前言 提示:这里可以添加本文要记录的大概内容: 例如:…...

WebView2 Win7下部分机器触屏失效的问题
这个问题官方给了解决的方案,相关地址,只需要在项目中运行这个代码即可 public static void DisableWPFTabletSupport(){TabletDeviceCollection devices Tablet.TabletDevices;if (devices.Count > 0){Type inputManagerType typeof(InputManager)…...

Ubuntu 通过指令远程命令行配置WiFi连接
前提设备已经安装了无线网卡。 1、先通过命令行 ssh 登录机器。 2、搜索wifi设备,指令如下: sudo nmcli device wifi 3、输入需要联接的 wifi 名称和对应的wifi密码,指令如下: sudo nmcli device wifi connect wifi名称 passw…...

线程池优雅关闭的哲学
引言 关于并发的哲学,本文将着重强调那些关于线程池优雅关闭的一些技巧,希望对你有所启发。 强制关闭线程池的弊端 对于池化的线程池,如果采用强制关闭的方式将线程池直接关闭,就可能存在上下文消息消息,无法的很好…...

11.8 LangGraph生产级AI Agent开发:从节点定义到高并发架构的终极指南
使用 LangGraph 构建生产级 AI Agent:LangGraph 节点与边的实现 关键词:LangGraph 节点定义, 条件边实现, 状态管理, 多会话控制, 生产级 Agent 架构 1. LangGraph 核心设计解析 LangGraph 通过图结构抽象复杂 AI 工作流,其核心要素构成如下表所示: 组件作用描述代码对应…...

8天Python从入门到精通【itheima】-41~44
目录 41节-while循环的嵌套应用 1.学习目标 2.while循环的伪代码和生活情境中的应用 3.图片应用的代码案例 4.代码实例【Patrick自己亲手写的】: 5.whlie嵌套循环的注意点 6.小节总结 42节-while循环的嵌套案例-九九乘法表 1.补充知识-print的不换行 2.补充…...
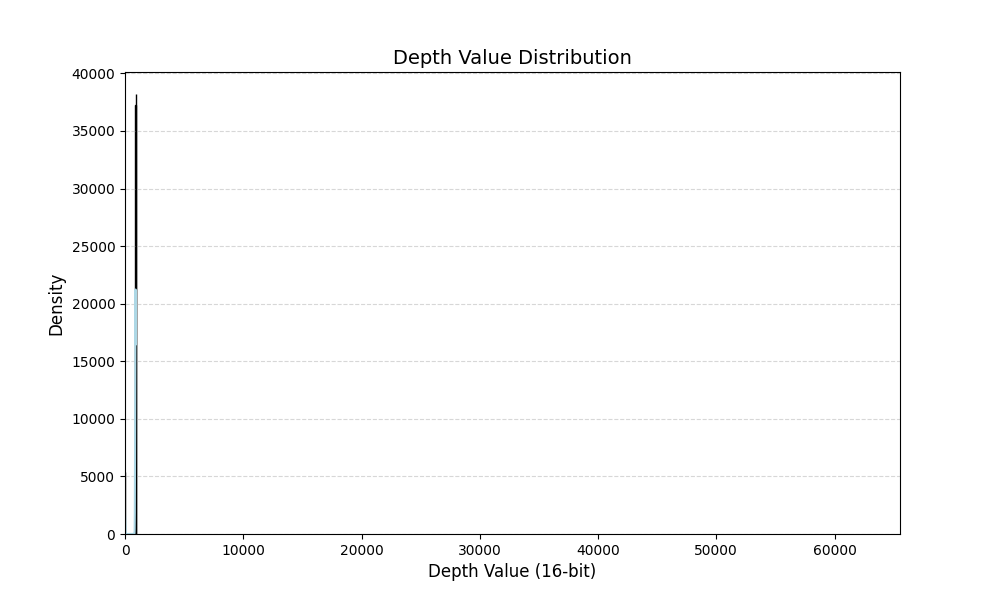
深度图数据增强方案-随机增加ROI区域的深度
主要思想:随机增加ROI区域的深度,模拟物体处在不同位置的形态。 首先打印一张深度图中的深度信息分布: import cv2 import matplotlib.pyplot as plt import numpy as np import seaborn as sns def plot_grayscale_histogram(image_path)…...

[Java恶补day6] 15. 三数之和
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请你返回所有和为 0 且不重复的三元组。 注意:答案中不可以包含重复的三元组。 示例 1&a…...

Django模板及表单
什么是Django模板 Django模板是一种用于生成动态内容的文件,它使用Django模板语言(Django Template Language,简称DTL)来描述和渲染HTML页面。模板允许开发人员将动态数据与静态HTML结构分离,以实现更灵活和可维护的W…...
