力扣经典算法篇-13-接雨水(较难,动态规划,加法转减法优化,双指针法)
1、题干
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:

输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
提示:
n == height.length
1 <= n <= 2 * 104
0 <= height[i] <= 105
2、解题
方法一:动态规划,加法转减法思路
对于接雨水这个问题,正向来看,我们需要求出每一个柱子雨水部分的面积,然后累加得到最终的雨水量。
这个思路最容易想到,也能做,但计算相对比较麻烦,需要分别计算出每一个柱子左右两边最大值。然后取其中较小的一个减去当前柱子高度,获取当前柱子的储水量,依次遍历累加获取最终的储水量。这里我们不推荐。
反向来看,柱子的高度已知,我们可以求出当前总面积,在减去每一个柱子的面积,剩下的就是储水量的和。
这个思路就是把加法转化为减法。根据特征可以看出,左边到最高值一定是递增的,最高值到最右边又依次是递减的。
以左边为例,求当前柱子的最终高度,是不是就是左边存在的最大值,把这个最大值提取出来当做公共变量依次求出每一个柱子的最终值。
代码示例:
// 动态规划,加法转减法基础思路public static int trap(int[] height) {int sum = 0;// 1、求出最大元素的下标,可能是多个int max = Arrays.stream(height).max().getAsInt();List<Integer> maxIndexList = new ArrayList<>();for (int i = 0; i < height.length; i++) {if (height[i]==max){maxIndexList.add(i);}}// 多个最大值时,最终高度就是max,求取这部分的雨水if (maxIndexList.size()>1){for (int i = maxIndexList.get(0)+1; i < maxIndexList.get(maxIndexList.size()-1); i++) {sum = sum + (max-height[i]);}}// 2、求出最左的递增序列,计算左侧雨水int leftMaxIndex = maxIndexList.get(0);int leftmax = height[0];for (int i = 1; i < leftMaxIndex; i++) { // 最边上的柱子不可能有雨水,从1开始if (height[i]>leftmax){leftmax = height[i];}sum = sum + (leftmax-height[i]);}// 3、求出最右的递减序列,计算左侧雨水int rightMaxIndex = maxIndexList.get(maxIndexList.size()-1);int rightmax = height[height.length-1];for (int i = height.length-2; i > rightMaxIndex; i--) { // 最边上的柱子不可能有雨水,从1开始if (height[i]>rightmax){rightmax = height[i];}sum = sum + (rightmax-height[i]);}return sum;}
方法二:动态规划,加法转减法思路优化
思路和方法一是一致的,主要用于优化时间复杂度。
从左到右遍历获取最大值数组1,在从右向左获取最大数组2。两者取较小值就是当前柱子的最小高度。
这个方法只需要两次遍历,时间复杂度为O(n),计算起来效率比方法一要更高。
左侧求解示例图:
如下红色部分为左侧开始遍历得到的结果集。

右侧求解示例图:
如下红色部分为右侧遍历得到的结果集。

两者取最小的部分得到:

代码示例:
// 动态规划,加法转减法基础思路,优化方案public static int trap(int[] height) {int sum = 0;// 1、求出从左到右的最大值序列int[] maxLeft = new int[height.length];int maxTemp = 0;for (int i = 0; i < height.length; i++) {if (height[i]>maxTemp){maxTemp = height[i];}maxLeft[i] = maxTemp;}// 2、反向求出从右到左的最大值序列int[] maxRight = new int[height.length];maxTemp = 0;for (int i = height.length-1; i >= 0; i--) {if (height[i]>maxTemp){maxTemp = height[i];}maxRight[i] = maxTemp;}// 两者最小值减去height就是当前节点的雨水量for (int i = 0; i < height.length; i++) {sum = sum + (Math.min(maxRight[i],maxLeft[i]) - height[i]);}return sum;}
方法三:双指针法
这个思路和上面的方法有些类似的。使用双指针分别指向最左和最右,依次求解左和右较小的那一部分获取雨水值,直到指针相遇结束。
代码示例:
public static int trap(int[] height) {int ans = 0;int left = 0, right = height.length - 1;int leftMax = 0, rightMax = 0; // 记录最左和最右已存在的最大值while (left < right) {leftMax = Math.max(leftMax, height[left]);rightMax = Math.max(rightMax, height[right]);if (height[left] < height[right]) {ans += leftMax - height[left];++left;} else {ans += rightMax - height[right];--right;}}return ans;}
向阳出发,Dare To Be!!!
相关文章:

力扣经典算法篇-13-接雨水(较难,动态规划,加法转减法优化,双指针法)
1、题干 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 示例 1: 输入:height [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,3…...
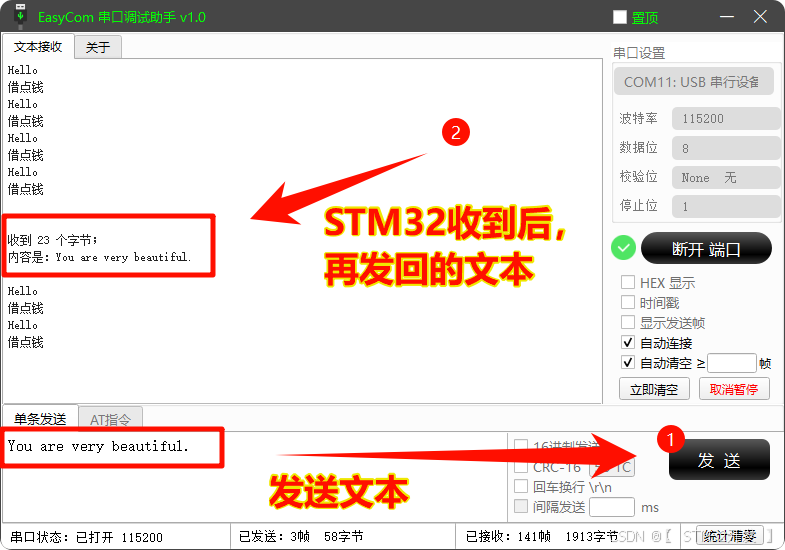
STM32 -- USB虚拟串口通信
本篇操作: 通过CubeMX Keil,配置STM32作为USB设备端,与电脑上位机进行通信(CDC);通用带USB功能的 STM32 芯片 (如F1、F4等,系统时钟配置不同,代码通用)。 目录 一、 S…...
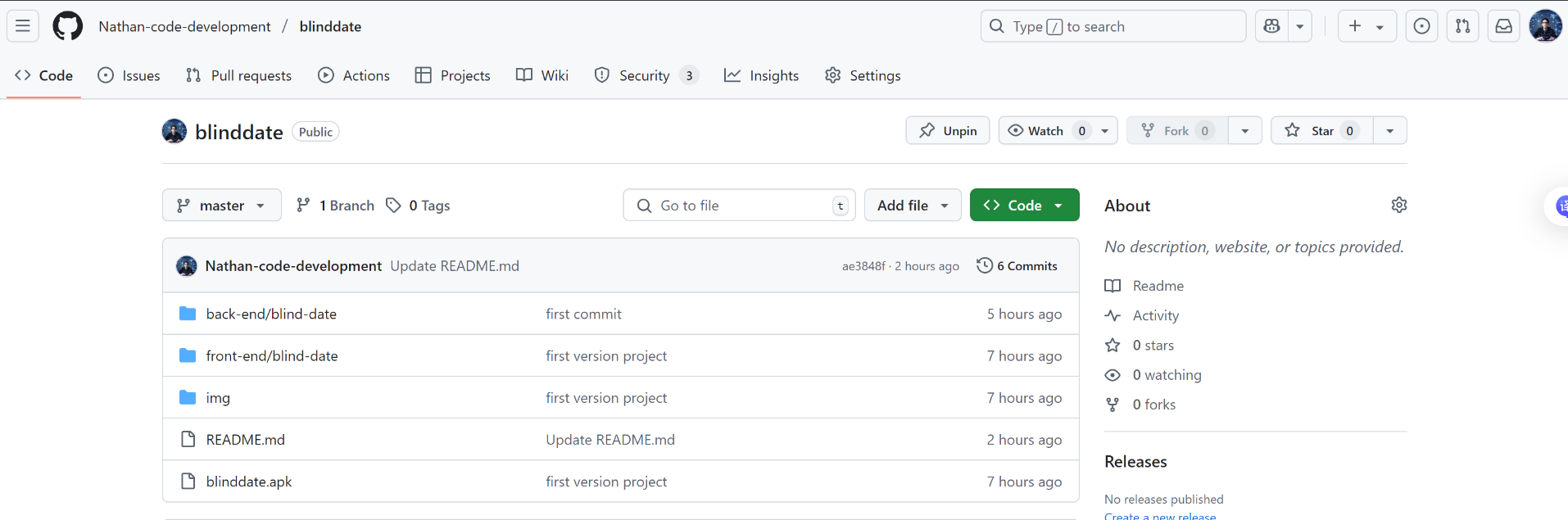
uni-app开发特殊社交APP
uni-app开发特殊社交APP 目录 1.展示APP功能 2.展示项目结构 3.关于我的GitHub 引言 博主最近自己在GitHub上面上传了一个关于社交软件的项目(该项目早已开发完毕), 这个社交软件比较特殊, 被称之为blind-date, blind-date 是基于 uni-…...

Linux中Shell脚本的常用命令
一、设置主机名称 1、通过修改系统文件来修改主机名称 [rootsakura1 桌面]# vim /etc/hostname sakura /etc/hostname:Linux 系统中存储主机名的配置文件。修改完文件后,在当前的shell中是不生效的,需要关闭当前shell后重新开启才能看到效…...

RabbitMQ项目实战
先参考文章:(必看) 06-MQ基础_mq服务-CSDN博客 07-MQ高级(幂等性)-CSDN博客 https://cloud.iocoder.cn/message-queue/rabbitmq/#_2-0-%E5%BC%95%E5%85%A5%E4%BE%9D%E8%B5%96%E4%B8%8E%E9%85%8D%E7%BD%AE 1、Rabbi…...

安卓开发用到的设计模式(3)行为型模式
安卓开发用到的设计模式(3)行为型模式 文章目录 安卓开发用到的设计模式(3)行为型模式1. 命令模式(Command Pattern)2. 策略模式(Strategy Pattern)3. 观察者模式(Observ…...

生成模型:从数据学习到创造的 AI 新范式
一、生成模型:定义与核心逻辑 生成模型是一类通过学习数据潜在分布来创造新样本的机器学习模型。其核心目标是构建数据的概率分布模型 P(X),使生成的样本 X^ 与真实数据 X 具有相似的统计特征。 1.1 与判别模型的本质区别 维度生成模型判别模型核心目…...

尚硅谷redis7 90-92 redis集群分片之集群扩容
90 redis集群分片之集群扩容 三主三从不够用了,进行扩容变为4主4从 问题:1.新建两个redis实例,怎么加入原有集群?2.原有的槽位分3段,又加进来一个槽位怎么算? 新建6387、6388两个服务实例配置文件新建后启…...

RabbitMQ性能调优:关键技术、技巧与最佳实践
RabbitMQ作为一款高可靠、高扩展性的消息中间件,其性能表现直接影响到分布式系统的吞吐量和响应延迟。本文基于RabbitMQ官方文档和最佳实践,结合核心性能优化方向,详细探讨RabbitMQ性能调优的关键技术、技巧和策略。 通过以下优化策略&#…...

系统架构中的组织驱动:康威定律在系统设计中的应用
康威定律(Conway’s Law) 是由计算机科学家 Melvin Conway 在1967年提出的理论,其核心观点是:“系统的架构设计会不可避免地反映其开发组织的沟通结构。换句话说,软件系统的结构会与构建它的团队的组织结构高度相似。 …...

TypeScript 中高级类型 keyof 与 typeof的场景剖析。
文章目录 前言一、typeof:从值到类型的映射1. 核心概念2. 类型推导示例3. 常见用途 二、keyof:从类型到键的映射1. 核心概念2. 常见用途 三、typeof keyof:强强联合的实战场景1. 场景一:对象属性的安全访问2. 场景二:…...

Android LiveData 详解
一、LiveData 核心概念与特性 1.1 定义与基本功能 LiveData 是 Android Jetpack 架构组件中的一个可观察数据持有者类,其核心功能是实现数据与 UI 的响应式绑定。与传统观察者模式不同,LiveData 具有生命周期感知能力,能够自动根据观察者…...

为什么共现矩阵是高维稀疏的
为什么共现矩阵是高维稀疏的? 共现矩阵(Co-occurrence Matrix)的高维稀疏性是其固有特性,主要由以下原因导致: 1. 高维性的根本原因 词汇表大小决定维度: 共现矩阵的维度为 ( V \times V ),其…...

离散化算法的二分法应用
我们思考一个问题:其实这里的二分法回归本源也是基于下标映射的原理,只是实现是借助二分的形式。 在排序好的数组中对目标数值进行二分搜索,在 O(logn) 的时间复杂度内找到该数值是整体数据中的第几个。 具体的我们可以如下操作: …...

IntelliJ IDEA 中进行背景设置
🎨 一、全局主题切换 操作路径 File → Settings → Appearance & Behavior → Appearance → Theme可选主题: Darcula:深色模式(默认暗黑主题)IntelliJ Lightÿ…...

Dart语言学习指南「专栏简介」
Dart 是 Google 开发的一款开源通用编程语言,它不仅支持客户端和服务器端的应用开发,还因其与 Flutter 框架的深度集成,在移动端和 Web 开发中广受欢迎。Dart 适用于 Android 应用、iOS 应用、物联网(IoT)项目以及 Web…...

AWS之AI服务
目录 一、AWS AI布局 1. 底层基础设施与芯片 2. AI训练框架与平台 3. 大模型与应用层 4. 超级计算与网络 与竞品对比 AI服务 1. 机器学习平台 2. 预训练AI服务 3. 边缘与物联网AI 4. 数据与AI…...

Docker 部署项目
使用 Docker 部署项目是一个很好的选择,可以避免服务器环境不兼容的问题,并且能够实现一致性和可移植性。我会给你一个详细的步骤,帮你从零开始理解 Docker,最终在服务器上部署 Roop 项目。 1. 安装 Docker 首先,你需…...

半导体厂房设计建造流程、方案和技术要点-江苏泊苏系统集成有限公司
半导体厂房设计建造流程、方案和技术要点-江苏泊苏系统集成有限公司 半导体厂房的设计建造是一项高度复杂、专业性极强的系统工程,涉及洁净室、微振动控制、电磁屏蔽、特殊气体/化学品管理等关键技术。 一、设计建造流程: 1.需求定义与可行性分析 &a…...
string的模拟实现)
(c++)string的模拟实现
目录 1.构造函数 2.析构函数 3.扩容 1.reserve(扩容不初始化) 2.resize(扩容加初始化) 4.push_back 5.append 6. 运算符重载 1.一个字符 2.一个字符串 7 []运算符重载 8.find 1.找一个字符 2.找一个字符串 9.insert 1.插入一个字符 2.插入一个字符串 9.erase 10…...

一种通用图片红色印章去除的工具设计
朋友今天下午需要处理个事情,问我有没有什么好的办法能够去除,核心问题是要去除图片上的印章。记得以前处理过类似的需求,photoshop操作比较简单,本质是做运算。这种处理方式有很多,比如现在流行的大模型,一…...

企业应用AI对向量数据库选型思考
一、向量数据库概述 向量数据库是一种专门用于存储和检索高维向量数据的数据库系统,它能够高效地处理基于向量相似性的查询,如最近邻搜索等,在人工智能、机器学习等领域的应用中发挥着重要作用,为处理复杂的向量数据提供了有力的…...

时序数据库IoTDB安装学习经验分享
1. JDK安装问题 在安装IoTDB时,我遇到了“无法加载主类”的错误,这通常表明Java环境存在问题。尽管我能正确输出classpath和查询JDK版本,但问题依旧存在。经过查阅相关资料,我发现问题出在多余的classpath设置上。Java编译器和虚…...

RapidOCR集成PP-OCRv5_det mobile模型记录
该文章主要摘取记录RapidOCR集成PP-OCRv5_mobile_det记录,涉及模型转换,模型精度测试等步骤。原文请前往官方博客: https://rapidai.github.io/RapidOCRDocs/main/blog/2025/05/26/rapidocr%E9%9B%86%E6%88%90pp-ocrv5_det%E6%A8%A1%E5%9E%8B…...
之间的一致性?)
当 Redis 作为缓存使用时,如何保证缓存数据与数据库(或其他服务的数据源)之间的一致性?
当 Redis 作为缓存使用时,保证缓存数据与数据库(或其他数据源)之间的一致性是一个核心挑战。通常,我们追求的是“最终一致性”,而不是“强一致性”,因为强一致性往往会牺牲性能和可用性,这与使用…...

Dify理论+部署+实战
概述 一个功能强大的开源AI应用开发平台,融合后端即服务(Backend as Service)和LLMOps理念,使开发者能够快速搭建生产级的生成式AI应用。 核心优势 直观的用户界面:提供简洁明了的操作界面,使得用户能够…...

内网穿透系列五:自建SSH隧道实现内网穿透与端口转发,Docker快速部署
以下是对这个自建SSH隧道工具的简单介绍: 一款基于OpenSSH构建的内网穿透与端口转发工具,通过SSH隧道技术实现支持所有TCP协议通信,包括SSH、HTTP、HTTPS等各类应用提供灵活部署方式,特别支持Docker容器化快速部署开源工具地址…...

桥梁进行3D建模时的数据采集、存储需求及技术参数
桥梁进行3D建模时的数据采集、存储需求及技术参数 1公里桥梁进行3D建模时的数据采集、存储需求及技术参数的详细分析 1. 照片数量估算 关键影响因素 桥梁类型:梁桥/拱桥/斜拉桥(结构复杂度不同) 建模精度:工程级(1-…...

Transformer架构技术学习笔记:从理论到实战的完整解析
引言:重新定义序列建模的里程碑 2017年,Vaswani等人在论文《Attention Is All You Need》中提出的Transformer架构,彻底改变了自然语言处理领域的游戏规则。与传统RNN/LSTM相比,Transformer具有三大革命性特征: 全注意…...

1、python代码实现与大模型的问答交互
一、基础知识 1.1导入库 torch 是一个深度学习框架,用于处理张量和神经网络。modelscope是由阿里巴巴达摩院推出的开源模型库。 AutoTokenizer 是ModelScope 库的类,分词器应用场景包括自然语言处理(NLP)中的文本分类、信息抽取…...
