UVa12298 Super Joker II
UVa12298 Super Joker II
- 题目链接
- 题意
- 输入格式
- 输出格式
- 分析
- AC 代码
题目链接
UVa12298 Super Joker II
题意
有一副超级扑克,包含无数张牌。对于每个正合数p,恰好有4张牌:黑桃p,红桃p,梅花p和方块p(分别用pS、pH、pC 和pD 表示)。没有其他类型的牌。
给定一个整数n,从4种花色中各选一张牌,问有多少种组合可以使得点数之和等于n。例如,n=24的时候,有一种组合方法是4S+6H+4C+10D,下图所示。

不巧的是,有些牌已经丢失(题目会提供已经丢失的牌的列表)。并且为了让题目更有趣,我们还会提供两个正整数a和b,你的任务是按顺序输出n=a, n=a+1, n=a+2, …, n=b时的答案。
输入格式
输入包含不超过25组数据。每组数据的第一行为3个整数a, b, c,其中c是已丢失的牌的张数。第二行包含c个不同的字符串,即已丢失的牌。这些牌形如pS, pH, pC 或者pD,其中p是一个正合数。输入结束标志为a=b=c=0。最多有一组数据满足a=1, b=50000且c≤10000,其他数据满足1≤a≤b≤100, 0≤c≤10。
输出格式
对于每组数据,输出p 行,每行一个整数。每组数据后输出一个空行。
分析
只需要对生成函数理解清楚了,就可以套用快速傅里叶变换(FFT)求解。初次接触FFT的话,推荐看看这篇知乎,GhostLX大佬给出了模板:
void dft(Complex a[])
{for (int i = 0; i < tot; i++){if (i < rev[i])swap(a[i], a[rev[i]]); //只需要交换一次就行了,交换两次等于没有换}for (int mid = 1; mid < tot; mid <<= 1){auto w1 = Complex({cos(PI / mid), sin(PI / mid)});for (int i = 0; i < tot; i += mid * 2){auto wk = Complex({1, 0}); //初始为w(0,mid)for (int j = 0; j < mid; j++, wk = wk * w1) //单位根递推式{auto x = a[i + j], y = wk * a[i + j + mid];a[i + j] = x + y, a[i + j + mid] = x - y;}}}
}
GhostLX大佬模板的单位根递推式像这样写wk = wk * w1,随着递推加深其实会带来精度误差的。推荐用这个模板:
namespace fft {#include <cmath>#define N 1<<21int res[N], tot;struct complex {double x, y;void operator+= (const complex &t) {x += t.x; y += t.y;}complex operator- (const complex &t) const {return {x - t.x, y - t.y};}complex operator* (const complex &t) const {return {x * t.x - y * t.y, x * t.y + y * t.x};}} a[N], b[N];/*** inv=1时求的是傅里叶变换(DFT),inv=-1时求的是傅里叶逆变换(IDFT)*/void fft(complex (&a)[N], int inv) {for (int i=0, j=0; i<tot; ++i) { // 原地快速bit reversalif(j > i) {complex t = a[i]; a[i] = a[j]; a[j] = t;}int k = tot;while(j & (k >>= 1)) j &= ~k;j |= k;}for(int step=1; step<tot; step<<=1) {// 把每相邻两个“step点DFT”通过一系列蝴蝶变换合并为一个“2*step点DFT”double alpha = inv*M_PI / step;// 为求高效,我们并不是依次执行各个完整的DFT合并,而是枚举下标k// 对于一个下标k,执行所有DFT合并中该下标对应的蝴蝶变换,即通过E[k]和O[k]计算X[k]// 蝴蝶变换参考:http://en.wikipedia.org/wiki/Butterfly_diagramfor(int k=0; k<step; k++) {// 计算omega^kcomplex wk = {cos(alpha*k), sin(alpha*k)};for(int Ek=k; Ek<tot; Ek += step<<1) { // Ek是某次DFT合并中E[k]在原始序列中的下标int Ok = Ek + step; // Ok是该DFT合并中O[k]在原始序列中的下标complex t = wk * a[Ok]; // 蝴蝶变换:x1 * omega^ka[Ok] = a[Ek] - t; // 蝴蝶变换:y1 = x0 - ta[Ek] += t; // 蝴蝶变换:y0 = x0 + t}}}}void workFFT(int n, int m) { // a[0, n], b[0, m]int bit = 0;while ((1 << bit) < n + m + 1) ++bit;tot = 1 << bit;fft(a, 1); fft(b, 1);for (int i=0; i<tot; ++i) a[i] = a[i] * b[i]; //点表示法直接运算fft(a, -1); //逆变换,点表示法转换为多项式表示法for (int i=0, j=m+n; i<=j; ++i) res[i] = a[i].x / tot + 0.5; //向上取整}
}
AC 代码
#include <iostream>
#include <cmath>
using namespace std;#define M 50020
#define N 1<<17
int na, nb, nc, tot; bool f[M] = {false};
struct complex {double x, y;void operator+= (const complex &t) {x += t.x; y += t.y;}complex operator- (const complex &t) const {return {x - t.x, y - t.y};}complex operator* (const complex &t) const {return {x * t.x - y * t.y, x * t.y + y * t.x};}} a[4][N];void fft(complex (&a)[N], int inv) {for (int i=0, j=0, k; i<tot; ++i) {if(j > i) {complex t = a[i]; a[i] = a[j]; a[j] = t;}for (k = tot; j & (k >>= 1); j &= ~k);j |= k;}for(int step=1; step<tot; step<<=1) {double alpha = inv*M_PI / step;for(int k=0; k<step; k++) {complex wk = {cos(alpha*k), sin(alpha*k)};for(int Ek=k; Ek<tot; Ek += step<<1) {int Ok = Ek + step; complex t = wk * a[Ok];a[Ok] = a[Ek] - t; a[Ek] += t;}}}
}void solve() {int bit = 0; tot = (nb<<1) | 1;while ((1 << bit) < tot) ++bit;tot = 1 << bit;for (int i=0; i<tot; ++i) a[0][i] = a[1][i] = a[2][i] = a[3][i] = {i<nb && f[i] ? 1. : 0., 0.};while (nc--) {int v; char h; cin >> v >> h;a[h == 'S' ? 0 : (h == 'H' ? 1 : (h == 'C' ? 2 : 3))][v].x = 0.;}for (int i=0; i<4; ++i) fft(a[i], 1);for (int i=0; i<tot; ++i) a[0][i] = a[0][i] * a[1][i], a[2][i] = a[2][i] * a[3][i];fft(a[0], -1); fft(a[2], -1);for (int i=0; i<tot; ++i) a[0][i] = {i<nb ? a[0][i].x / tot : 0., 0.}, a[2][i] = {i<nb ? a[2][i].x / tot : 0., 0.};fft(a[0], 1); fft(a[2], 1);for (int i=0; i<tot; ++i) a[0][i] = a[0][i] * a[2][i];fft(a[0], -1);for (int i=na; i<=nb; ++i) cout << (long long)(a[0][i].x / tot + .5) << endl;cout << endl;
}int main() {for (int i=2; i*i<M; ++i) if (!f[i]) for (int j=i*i; j<M; j+=i) f[j] = true;while (cin >> na >> nb >> nc && (na || nb || nc)) solve();return 0;
}
相关文章:

UVa12298 Super Joker II
UVa12298 Super Joker II 题目链接题意输入格式输出格式 分析AC 代码 题目链接 UVa12298 Super Joker II 题意 有一副超级扑克,包含无数张牌。对于每个正合数p,恰好有4张牌:黑桃p,红桃p,梅花p和方块p(分别…...

面向对象系统中对象交互的架构设计哲学
更多精彩请访问:通义灵码2.5——基于编程智能体开发Wiki多功能搜索引擎-CSDN博客 一、对象交互的本质与设计矛盾 在面向对象范式(OOP)中,对象间的交互实质上是软件组件解耦与功能复用的动态平衡过程。每个对象作为独立的计算单元,既需要维护…...

【网络安全】SRC漏洞挖掘思路/手法分享
文章目录 Tip1Tip2Tip3Tip4Tip5Tip6Tip7Tip8Tip9Tip10Tip11Tip12Tip13Tip14Tip15Tip16Tip17Tip18Tip19Tip20Tip21Tip22Tip23Tip24Tip25Tip26Tip27Tip28Tip29Tip30Tip1 “复制该主机所有 URL”:包含该主机上的所有接口等资源。 “复制此主机里的链接”:包括该主机加载的第三…...

【AFW+GRU(CNN+RNN)】Deepfakes Detection with Automatic Face Weighting
文章目录 Deepfakes Detection with Automatic Face Weighting背景pointsDeepfake检测挑战数据集方法人脸检测面部特征提取自动人脸加权门控循环单元训练流程提升网络测试时间增强实验结果Deepfakes Detection with Automatic Face Weighting 会议/期刊:CVPRW 2020 作者: …...

【面试】音视频面试
C内存模型 H.265(HEVC)相比H.264(AVC)的核心优势 1. 压缩效率显著提升 在相同画质下,H.265的码率比H.264降低约40-50%,尤其适用于4K/8K超高清场景。通过**更大的编码单元(CTU,最大…...

性能优化 - 案例篇:缓冲区
文章目录 Pre1. 引言2. 缓冲概念与类比3. Java I/O 中的缓冲实现3.1 FileReader vs BufferedReader:装饰者模式设计3.2 BufferedInputStream 源码剖析3.2.1 缓冲区大小的权衡与默认值 4. 异步日志中的缓冲:Logback 异步日志原理与配置要点4.1 Logback 异…...

Java编程之建造者模式
建造者模式(Builder Pattern)是一种创建型设计模式,它将一个复杂对象的构建与表示分离,使得同样的构建过程可以创建不同的表示。这种模式允许你分步骤构建一个复杂对象,并且可以在构建过程中进行不同的配置。 模式的核…...

基于TI DSP控制的光伏逆变器最大功率跟踪mppt
基于TI DSP(如TMS320F28335)控制的光伏逆变器最大功率跟踪(MPPT)程序通常涉及以下几个关键部分:硬件电路设计、MPPT算法实现、以及DSP的编程。以下是基于TI DSP的光伏逆变器MPPT程序的一个示例,主要采用扰动…...

Python玩转自动驾驶仿真数据生成:打造你的智能“路测场”
Python玩转自动驾驶仿真数据生成:打造你的智能“路测场” 说到自动驾驶,很多人第一时间想到的是那些造车新势力、激光雷达、传感器、深度学习模型……确实,这些都是自动驾驶的核心硬核。但我今天想和你聊聊一个“幕后功臣”——仿真数据生成。没错,自动驾驶离不开大数据,更…...

从测试角度看待CI/CD,敏捷开发
什么是敏捷开发? 是在高强度反馈的情况下,短周期,不断的迭代产品,满足用户需求,抢占更多的市场 敏捷开发是什么? 是一种产品快速迭代的情况下,降低出错的概率,具体会落实到公司的…...

agent mode 代理模式,整体要求,系统要求, 系统指令
1. 起因, 目的: 我发现很多时候,我在重复我的要求。很烦。决定把一些过程记录下来,提取一下。 2. 先看效果 无。 3. 过程: 要求: 这2个文件,是我与 AI 聊天的一些过程记录。 请阅读这2个文件,帮我提取出一些共同…...

ES101系列07 | 分布式系统和分页
本篇文章主要讲解 ElasticSearch 中分布式系统的概念,包括节点、分片和并发控制等,同时还会提到分页遍历和深度遍历问题的解决方案。 节点 节点是一个 ElasticSearch 示例 其本质就是一个 Java 进程一个机器上可以运行多个示例但生产环境推荐只运行一个…...

Spring AI Advisor机制
Spring AI Advisors 是 Spring AI 框架中用于拦截和增强 AI 交互的核心组件,其设计灵感类似于 WebFilter,通过链式调用实现对请求和响应的处理5。以下是关键特性与实现细节: 核心功能 1. 请求/响应拦截 通过 AroundAdvisor 接口动态修…...
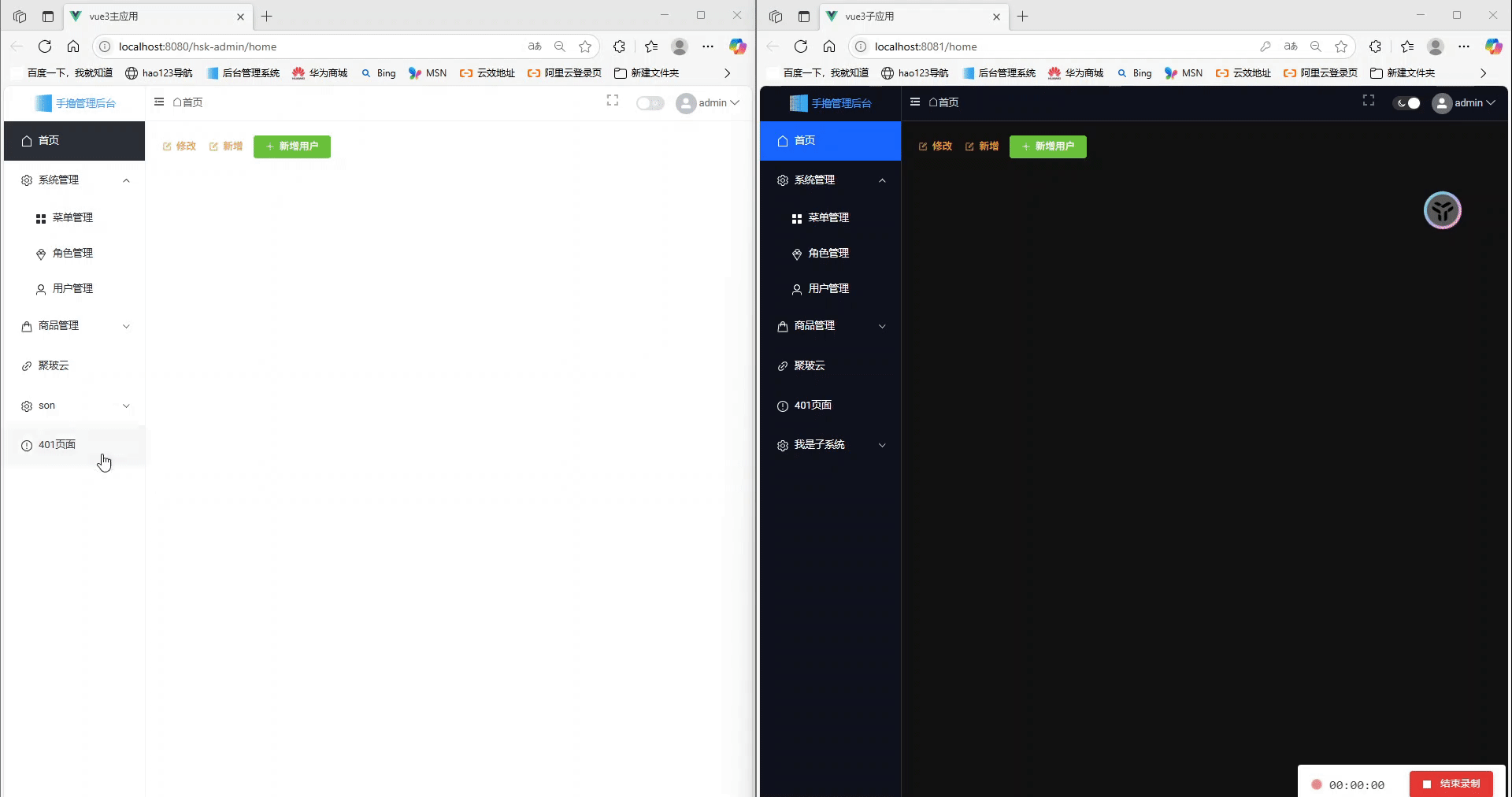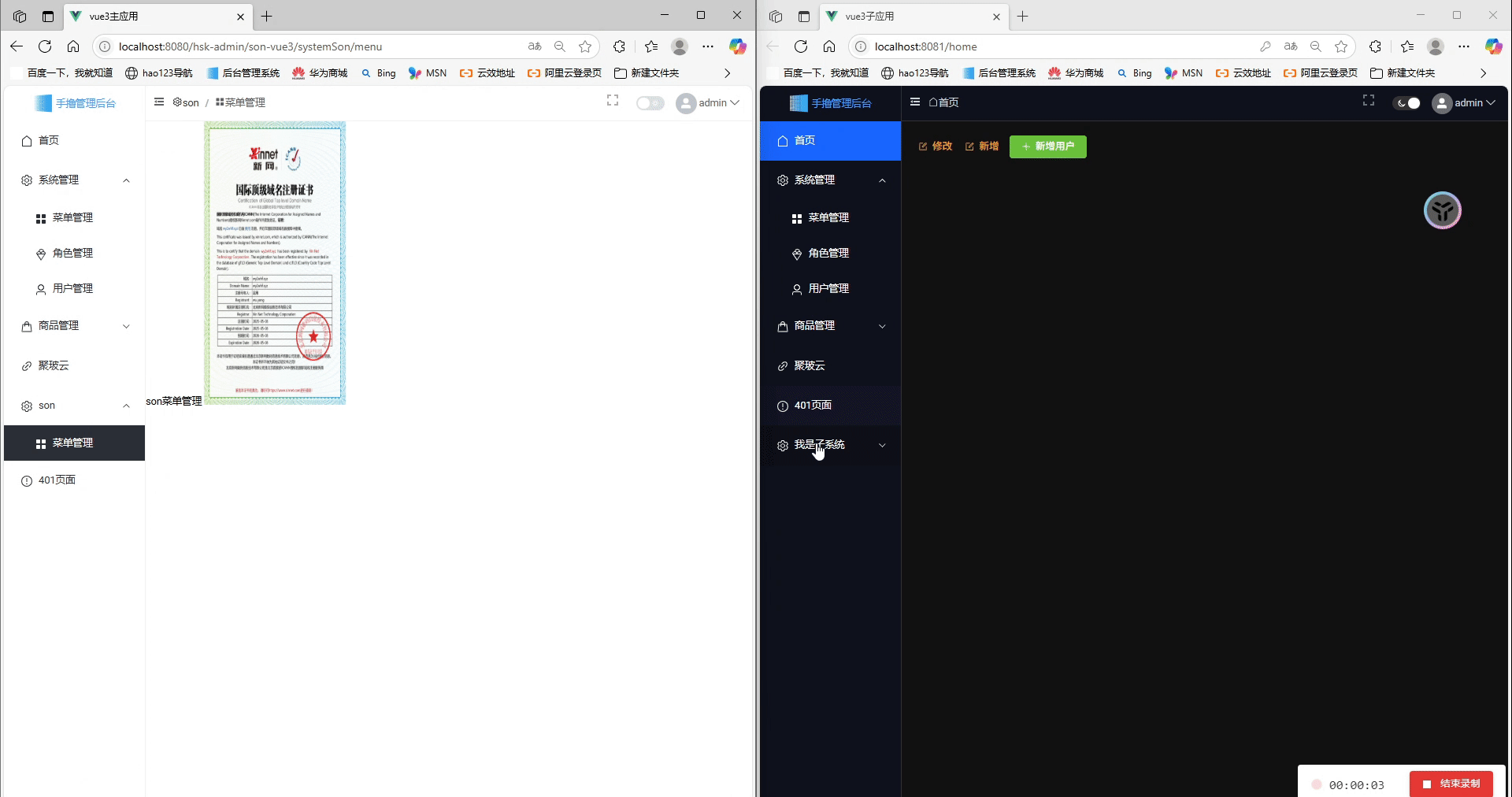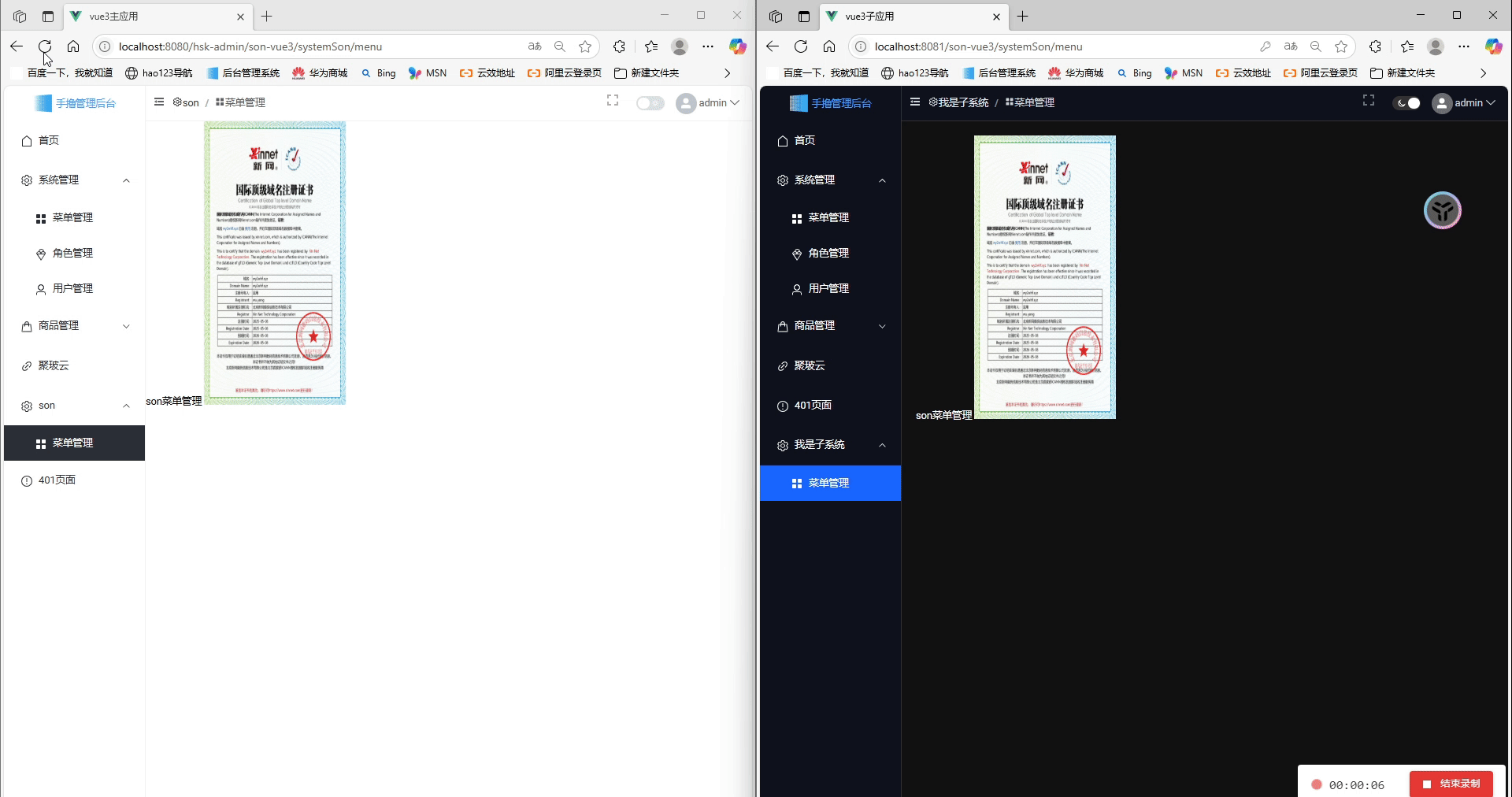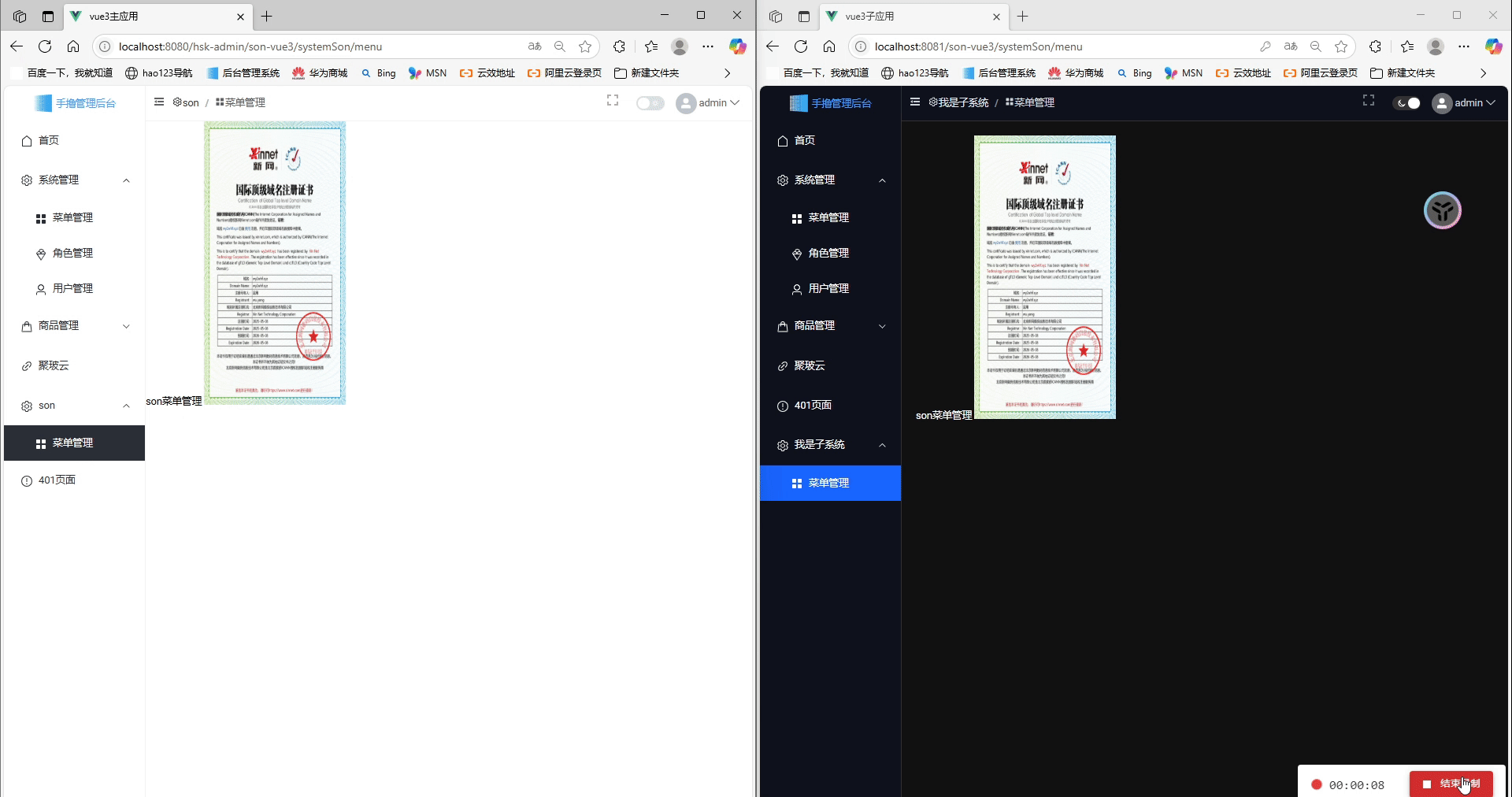
Vue3 + Vite:我的 Qiankun 微前端主子应用实践指南
前言 实践文章指南 vue微前端qiankun框架学习到项目实战,基座登录动态菜单及权限控制>>>>实战指南:Vue 2基座 Vue 3 Vite TypeScript微前端架构实现动态菜单与登录共享>>>>构建安全的Vue前后端分离架构:利用长Token与短Tok…...

使用ArcPy生成地图系列
设置地图布局 在生成地图系列之前,需要先设置地图布局。这包括定义地图的页面大小、地图框的位置和大小、标题、图例等元素。ArcPy提供了arcpy.mp.ArcGISProject方法来加载ArcGIS Pro项目文件(.aprx),并操作其中的地图布局。 Py…...

日语输入法怎么使用罗马字布局怎么安装日语输入法
今天帮客户安装日语输入法的时候遇到了一个纠结半天的问题,客户一直反馈说这个输入法不对,并不是他要的功能。他只需要罗马字的布局,而不是打出来字的假名。 片假名、平假名,就好像英文26个字母,用于组成日文单词。两…...

U盘挂载Linux
在 只能使用 Telnet 的情况下,如果希望通过 U盘 传输文件到 Linux 系统,可以按照以下步骤操作: 📌 前提条件 U盘已插入 Linux 主机的 USB 接口。Linux 主机支持自动挂载 U盘(大多数现代发行版默认支持)。T…...

数据结构:栈(Stack)和堆(Heap)
目录 内存(Memory)基础 程序是如何利用主存的? 🎯 静态内存分配 vs 动态内存分配 栈(stack) 程序执行过程与栈帧变化 堆(Heap) 程序运行时的主存布局 内存(Memo…...

用 Vue 做一个轻量离线的“待办清单 + 情绪打卡”小工具
网罗开发 (小红书、快手、视频号同名) 大家好,我是 展菲,目前在上市企业从事人工智能项目研发管理工作,平时热衷于分享各种编程领域的软硬技能知识以及前沿技术,包括iOS、前端、Harmony OS、Java、Python等…...

3D Gaussian splatting 05: 代码阅读-训练整体流程
目录 3D Gaussian splatting 01: 环境搭建3D Gaussian splatting 02: 快速评估3D Gaussian splatting 03: 用户数据训练和结果查看3D Gaussian splatting 04: 代码阅读-提取相机位姿和稀疏点云3D Gaussian splatting 05: 代码阅读-训练整体流程3D Gaussian splatting 06: 代码…...

Linux——计算机网络基础
一、网络 1.概念 由若干结点和连接结点的链路组成。结点可以是计算机,交换机,路由器等。 2.互联网 多个网络连接起来就是互联网。 因特网:最大的互联网。 二、IP地址和MAC地址 1.IP地址 (1)概念 IP地址是给因…...

第2章_Excel_知识点笔记
来自: 第2章_Excel_知识点笔记 原笔记 Excel 知识点总结(第2章) Excel_2.1 知识点 基础操作 状态栏:快速查看计数/求和等数据(右键可配置)。筛选(CtrlShiftL):按条件显…...

缩量和放量指的是什么?
在股票市场中,“缩量”和“放量”是描述成交量变化的两个核心概念,它们反映了市场参与者的情绪和资金动向,对判断股价趋势有重要参考价值。以下是具体解析: 📉 一、缩量(成交量明显减少) 1. 定…...

PostgreSQL数据库备份
文章目录 pg_dump 和 pg_dumpall使用 pg_dump 备份单个数据库示例 使用 pg_dumpall 备份整个数据库集群基本用法 恢复备份恢复 pg_dump 备份恢复 pg_dumpall 备份 Tips pg_dump 和 pg_dumpall 在 PostgreSQL 中,pg_dump 和 pg_dumpall 是两个常用的备份工具&#x…...

企业级Spring MVC高级主题与实用技术讲解
企业级Spring MVC高级主题与实用技术讲解 本手册旨在为具备Spring MVC基础的初学者,系统地讲解企业级应用开发中常用的高级主题和实用技术,涵盖RESTful API、统一异常处理、拦截器、文件处理、国际化、前端集成及Spring Security基础。内容结合JavaConf…...

js-day7
JS学习之旅-day7 1.事件流1.1 事件流与两个阶段说明1.2 事件捕获1.3 事件冒泡1.4 阻止1.5 解绑事件 2. 事件委托3. 其他事件3.1 页面加载事件3.2 页面滚动事件3.3 页面尺寸事件 4. 元素尺寸与位置 1.事件流 1.1 事件流与两个阶段说明 事件流指的是事件完整执行过程中的流动路…...

【算法训练营Day04】链表part2
文章目录 两两交换链表中的节点删除链表的倒数第 N 个结点链表相交环形链表 II链表总结 两两交换链表中的节点 题目链接:24. 两两交换链表中的节点 算法逻辑: 添加一个虚拟头节点初始化一个交换指针,代表每次交换指针的后两个节点࿰…...

【ROS2】各种相关概念汇总解释
包含概念 ROS2自带的标准接口ament_cmake是什么? 标准接口 似乎没有一个确定的名称,就是通俗的叫做“ROS2自带的消息接口” 这些接口存放在 /opt/ros/humble/share 路径下 ament_cmake 是 ROS 2 中基于 CMake 的构建系统 系统越复杂,构…...

解决Vditor加载Markdown网页很慢的问题(Vite+JS+Vditor)
1. 引言 在上一篇文章《使用Vditor将Markdown文档渲染成网页(ViteJSVditor)》中,详细介绍了通过Vditor将Markdown格式文档渲染成Web网页的过程,并且实现了图片格式居中以及图片源更换的功能。不过,笔者发现在加载这个渲染Markdown网页的时候…...

Flowise 本地部署文档及 MCP 使用说明
一、Flowise 简介 Flowise 是一个开源的拖放式 UI 工具,用于构建自定义的 LLM 工作流程。它允许用户通过可视化界面连接不同的 AI 组件,无需编写代码即可创建复杂的 AI 应用。 二、Docker 环境安装 1. 构建 Docker 镜像 docker build -t node22-ubuntu-dev .其中Dockerfi…...
