行列式的性质

1 行列式使用如下性质定义

1）单位矩阵行列式值为 1，

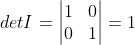
，对于任意单位矩阵均成立；

2）当矩阵交换一行后，行列式值改变符号，如置换矩阵的行列式值为 

（根据行交换次数决定）；

3）矩阵任意行线性变换导致行列式值产生线性变换：

      

，

 ；

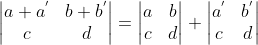
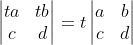
     使用以上三条基本性质，可以推导更多性质：

4）如果矩阵两行相等，行列式值为 0；

     利用性质2，交换两相等行，行列式值改变符号，故行列式值必须为 0；

5）对矩阵任意两行做如下运算：行2 = 行2 - k * 行1，新矩阵行列式值不发生改变，

     利用性质3，

 ；通过该性质，可以知道矩阵消元法仅改变矩阵行列式值的符号，

；

6）如果矩阵中存在一行全为 0， 矩阵行列式值为 0；

      利用性质5，将全零行改写为任意非零行与全零行的和，得到两个全零行，故原矩阵行列式值为 0；

7）上三角矩阵或者下三角矩阵行列式值为对角元素之积，

；

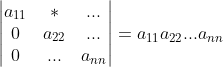
     a. 利用性质5，使用消元法可以对非零元素进行消元处理，最终形成对角矩阵，其对角元素保持不变，即 det U = det D；

     b. 利用性质3，

 ;

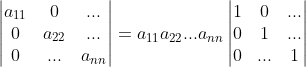
     c. 利用性质1，由于 

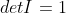
，则上三角矩阵行列式值为为对角元素之积；

8）如果矩阵为奇异矩阵，行列式值为 0；如果矩阵为非奇异矩阵，行列式值不为 0；

      当矩阵为奇异矩阵时，使用消元法至少一行全零行，性质5 表明 

, 根据性质6，det U = 0；

      当矩阵为非奇异矩阵时，使用消元法得到满秩，性质5 表明 

，根据性质7得 

；

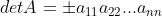
9）矩阵乘积的行列式等于矩阵行列式的乘积，

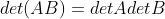
；使用该性质，有 

，

；

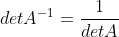
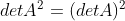
      a. 构造 

；

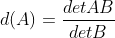
      b. 当 A 为单位矩阵时，

，满足性质1；

      c. 当交换矩阵 A 中任意两行，矩阵 AB 中对应两行也发送交换，d(A) 符号发生改变，满足性质2；

      d. 矩阵 A 中任意行线性变换，矩阵 AB 中对应行发生同样线性变换，d(A) 值发生同样线性变换，满足性质3；

      e. 综上，d(A) 满足性质1，2，3，故 

，

；

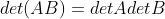
10）矩阵转置后行列式不发生改变，

；

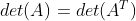
      a. 假定在不需行变换下可对矩阵进行 LU 分解，

；

      b. 利用性质9，

；

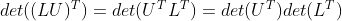
      c. 由于矩阵 L 为三角矩阵，且对角元素均为1，

；

      d. 由于矩阵 U 为三角矩阵，

，因此，

；

      e. 在矩阵 LU 分解时引入行变换，

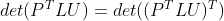
, 由于 

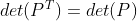
，故可忽略行变换影响；

2 行列式计算公式

   1）以3*3矩阵为例，使用行列式线性特性，将矩阵第一行进行分解：

      

；

  2）对分解后的三项对矩阵第二行再次分解：

     

，

     

，

     

；

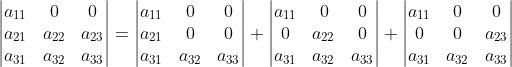
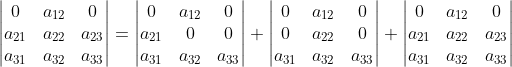
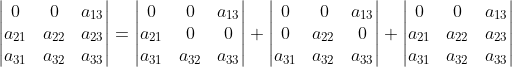
  3）对分解后的九项第三行再次分解：

     

，

     ...... 

  4）通过以上分解，3*3 矩阵的行列式被分解为 

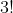
 个行列式的线性组合。在 27 个行列式中，有很大一部分值为 0，仅当各行元素不再同一列时，行列式值不为0。

       通过交换矩阵行，所有矩阵可变为对角矩阵，故行列式值公式可表示为：

      

，

     其中，

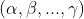
 为 

 的全排列，

 取决于在该排列下将矩阵变为对角矩阵的行变换次数的奇偶性，

     当行变换次数为奇数时，

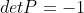
；当行变换次数为偶数时，

 。

3 代数余子式

   使用代数余子式，可以将 N 维行列式改写为 N - 1 维行列式得线性组合，降低计算量。方法如下：

   1）以 3*3 矩阵为例，其行列式值为

        

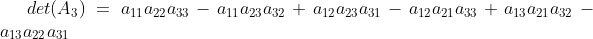
  2）提取公因子 

， 

       括号内部为余下 2*2 矩阵得行列式值（但符号可能相反）；

  3）将括号内记为对应元素得代数余子式，上式改写为 

，

；

  4）由于 

，因此也可以在列方向上分解行列式 

 。

4 行列式应用

  1）计算 

   使用 Gaussian-Jordan Method 可以通过消元法计算矩阵得逆，使用代数余子式概念可计算矩阵的逆，但效率会低于 Gaussian-Jordan Method。

   以 3*3 矩阵为例，解释如下：

   a. 矩阵 A 与代数余子式构成的矩阵 C 的转置相乘得：

      

；

   b. 上式中，如 

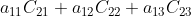
 等项表示原矩阵 A 使用第一行替代第二行构成的新矩阵 B 的行列式，由于 B 的第一行与第二行相等，故行列式值为 0；

       因此，只有当 a 与 C 的下标相同时，项 

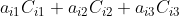
 的值等于 A  的行列式值，故上式可化简为：

       

；

   c. 进一步整理得 

，因此，

。

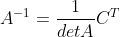
   2）求解 Ax=b

   a. 

，带入 

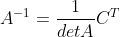
得 

；

   b. 向量 x 的各分量值 

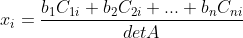
，其分子部分为一个新矩阵 

 的行列式值，

；

      因此，向量 x 的各分量值为 

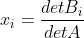
，这就是 Cramer's Rule 。

   3）多面体的体积

   在 N 维空间中，行列式值表示多面体体积。如在二维平面中，给定两条边构成的平行四边形面积等于以边为行构成的矩阵的行列式值（绝对值）；

   在三维空间中，给定三条边构成六面体的体积为对应矩阵的行列式值（绝对值）。证明如下：

   a. 当各条边相互垂直时，

；

       

， 

      

；

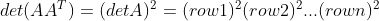
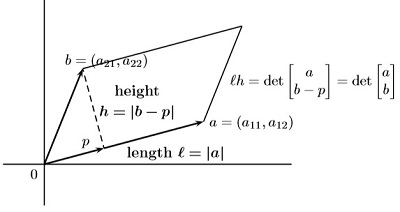
   b. 当各条边不垂直时，如下图所示，

；

       由于 

，根据 a 结论，

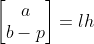
，因此，

，结论得证。