计算机视觉——相机标定
计算机视觉——相机标定
- 一、像素坐标系、图像坐标系、相机坐标系、世界坐标系
- 二、坐标系变换
- 图像坐标系 → 像素坐标系
- 相机坐标系 → 图像坐标系
- 世界坐标系 → 相机坐标系
- ⋆ \star ⋆ 世界坐标系 → 像素坐标系
- 三、相机标定
一、像素坐标系、图像坐标系、相机坐标系、世界坐标系
- 像素坐标系:数字图像在计算机内为 M × N M\times N M×N 的数组,其中每个元素(称为像素)的数值即是图像点的亮度(或称为灰度,彩色图像对应的为RGB)。在图像上定义直角坐标系 u , v u,v u,v,每一个像素的坐标 ( u , v ) (u,v) (u,v) 分别是该像素在数组中的列数与行数。
- 图像坐标系:以图像内某一点 O 1 O_1 O1 为原点, x x x 轴与 y y y 轴分别与 u , v u,v u,v轴平行,该坐标系中,原点 O 1 O_1 O1 定义在相机光轴与图像平面的交点,该点一般位于图像中心处。

- 相机坐标系:如图所示,其中 O O O 点称为相机光心, X c X_c Xc 轴和 Y c Y_c Yc 轴与图像的 x x x 轴与 y y y 轴平行, Z c Z_c Zc 轴为相机的光轴,它与图像平面垂直。光轴与图像平面的交点,即为图像物理坐标系的原点,由点 O O O 与 X c , Y c , Z c X_c,Y_c,Z_c Xc,Yc,Zc 轴组成的直角坐标系称为相机坐标系。 O O 1 OO_1 OO1 为相机焦距。
- 世界坐标系:由于相机可安放在环境中的任意位置,我们在环境中还需选择一个基准坐标系来描述相机的位置,并用它描述环境中任意物体的位置,该坐标系称为世界坐标系。它由 X w , Y w , Z w X_w,Y_w,Z_w Xw,Yw,Zw 轴组成。

二、坐标系变换
图像坐标系 → 像素坐标系
如图1所示,若 O 1 O_1 O1 在 u , v u,v u,v 坐标系中的坐标为 ( u 0 , v 0 ) (u_0,v_0) (u0,v0),每个像素在 x x x 轴与 y y y 轴方向上的物理尺寸为 d x , d y dx,dy dx,dy,单位:毫米(mm),则图像中任意一个像素在两个坐标系下的坐标有如下关系:
u = x d x + u 0 v = y d y + v 0 (1) \begin{aligned} u&=\frac{x}{dx}+u_0\\[2ex] v&=\frac{y}{dy}+v_0 \end{aligned}\tag{1} uv=dxx+u0=dyy+v0(1)
写成矩阵的形式:
[ u v 1 ] = [ 1 d x 0 u 0 0 1 d y v 0 0 0 1 ] [ x y 1 ] ⟺ [ x y 1 ] = [ d x 0 − u 0 d x 0 d y − v 0 d y 0 0 1 ] [ u v 1 ] (2) \left[ \begin{matrix} u \\[2ex] v \\[2ex] 1 \end{matrix} \right]= \left[ \begin{matrix} \dfrac{1}{dx} & 0 & u_0\\[2ex] 0 & \dfrac{1}{dy} & v_0\\[2ex] 0 & 0 & 1\\ \end{matrix} \right]\left[ \begin{matrix} x \\[2ex] y \\[2ex] 1 \end{matrix} \right] \quad\Longleftrightarrow\quad \left[ \begin{matrix} x \\[2ex] y \\[2ex] 1 \end{matrix} \right]= \left[ \begin{matrix} dx & 0 & -u_0dx\\[2ex] 0 & dy & -v_0dy\\[2ex] 0 & 0 & 1\\ \end{matrix} \right]\left[ \begin{matrix} u \\[2ex] v \\[2ex] 1 \end{matrix} \right]\tag{2} uv1 = dx1000dy10u0v01 xy1 ⟺ xy1 = dx000dy0−u0dx−v0dy1 uv1 (2)
相机坐标系 → 图像坐标系
如图2所示,相机坐标系中的点 ( X c , Y c , Z c ) (X_c,Y_c,Z_c) (Xc,Yc,Zc)投影到图像坐标系中的点为 ( x , y ) (x,y) (x,y)。根据相似三角形原理可以得到如下关系式:
x = f X c Z c , y = f Y c Z c (3) \begin{aligned} x=\dfrac{fX_c}{Z_c},\quad y=\dfrac{fY_c}{Z_c} \end{aligned}\tag{3} x=ZcfXc,y=ZcfYc(3)
写成矩阵的形式:
Z c [ x y 1 ] = [ f 0 0 0 0 f 0 0 0 0 1 0 ] [ X c Y c Z c 1 ] (4) Z_c\left[ \begin{matrix} x \\[2ex] y \\[2ex] 1 \end{matrix} \right]=\left[ \begin{matrix} f & 0 & 0 & 0\\[2ex] 0 & f & 0 & 0\\[2ex] 0 & 0 & 1 & 0\\ \end{matrix} \right]\left[ \begin{matrix} X_c \\[2ex] Y_c \\[2ex] Z_c \\[2ex] 1 \end{matrix} \right]\tag{4} Zc xy1 = f000f0001000 XcYcZc1 (4)
世界坐标系 → 相机坐标系
相机坐标系与世界坐标系之间的关系可以用旋转矩阵 R \pmb R R 与平移向量 t \pmb t t 来描述。因此,若空间中某一点 P \pmb P P 在世界坐标系与相机坐标系下的坐标分别为 ( X w , Y w , Z w , 1 ) T (X_w,Y_w,Z_w,1)^T (Xw,Yw,Zw,1)T 与 ( X c , Y c , Z c , 1 ) T (X_c,Y_c,Z_c,1)^T (Xc,Yc,Zc,1)T,于是存在如下关系:
[ X c Y c Z c 1 ] = [ R t 0 T 1 ] [ X w Y w Z w 1 ] = M 1 [ X w Y w Z w 1 ] (5) \left[ \begin{matrix} X_c \\[2ex] Y_c \\[2ex] Z_c \\[2ex] 1 \end{matrix} \right]= \left[ \begin{matrix} \pmb R & \pmb t\\[2ex] \ {\pmb 0}^T & 1 \end{matrix} \right]\left[ \begin{matrix} X_w \\[2ex] Y_w \\[2ex] Z_w \\[2ex] 1 \end{matrix} \right]=\pmb M_1\left[ \begin{matrix} X_w \\[2ex] Y_w \\[2ex] Z_w \\[2ex] 1 \end{matrix} \right]\tag{5} XcYcZc1 =[R 0Tt1] XwYwZw1 =M1 XwYwZw1 (5)
其中, R \pmb R R 为 3 × 3 3\times 3 3×3 单位正交矩阵, t \pmb t t 为三维平移向量, 0 = ( 0 , 0 , 0 ) T \pmb 0=(0,0,0)^T 0=(0,0,0)T, M 1 \pmb M_1 M1 为 4 × 4 4\times 4 4×4 矩阵。
⋆ \star ⋆ 世界坐标系 → 像素坐标系
联立式 ( 2 ) , ( 4 ) , ( 5 ) (2),(4),(5) (2),(4),(5),消去 ( x , y , 1 ) T , ( X c , Y c , Z c , 1 ) T (x,y,1)^T,(X_c,Y_c,Z_c,1)^T (x,y,1)T,(Xc,Yc,Zc,1)T,有,
Z c [ u v 1 ] = [ 1 d x 0 u 0 0 1 d y v 0 0 0 1 ] [ f 0 0 0 0 f 0 0 0 0 1 0 ] [ R t 0 T 1 ] [ X w Y w Z w 1 ] = [ a x 0 u 0 0 0 a y v 0 0 0 0 1 0 ] [ R t 0 T 1 ] [ X w Y w Z w 1 ] = M 1 M 2 [ X w Y w Z w 1 ] = M [ X w Y w Z w 1 ] (6) \begin{aligned} Z_c\left[ \begin{matrix} u \\[2ex] v \\[2ex] 1 \end{matrix} \right]&=\left[ \begin{matrix} \dfrac{1}{dx} & 0 & u_0\\[2ex] 0 & \dfrac{1}{dy} & v_0\\[2ex] 0 & 0 & 1\\ \end{matrix} \right]\left[ \begin{matrix} f & 0 & 0 & 0\\[2ex] 0 & f & 0 & 0\\[2ex] 0 & 0 & 1 & 0\\ \end{matrix} \right]\left[ \begin{matrix} \pmb R & \pmb t\\[2ex] \ {\pmb 0}^T & 1 \end{matrix} \right]\left[ \begin{matrix} X_w \\[2ex] Y_w \\[2ex] Z_w \\[2ex] 1 \end{matrix} \right]\\ &=\left[ \begin{matrix} a_x & 0 & u_0 & 0\\[2ex] 0 & a_y & v_0 & 0\\[2ex] 0 & 0 & 1 & 0\\ \end{matrix} \right]\left[ \begin{matrix} \pmb R & \pmb t\\[2ex] \ {\pmb 0}^T & 1 \end{matrix} \right]\left[ \begin{matrix} X_w \\[2ex] Y_w \\[2ex] Z_w \\[2ex] 1 \end{matrix} \right]\\ &=\pmb M_1\pmb M_2 \left[ \begin{matrix} X_w \\[2ex] Y_w \\[2ex] Z_w \\[2ex] 1 \end{matrix} \right]\\ &=\pmb M \left[ \begin{matrix} X_w \\[2ex] Y_w \\[2ex] Z_w \\[2ex] 1 \end{matrix} \right] \end{aligned}\tag{6} Zc uv1 = dx1000dy10u0v01 f000f0001000 [R 0Tt1] XwYwZw1 = ax000ay0u0v01000 [R 0Tt1] XwYwZw1 =M1M2 XwYwZw1 =M XwYwZw1 (6)
其中, a x = f d x , a y = f d y a_x=\dfrac{f}{dx},a_y=\dfrac{f}{dy} ax=dxf,ay=dyf, 由于 a x , a y , u 0 , v 0 a_x,a_y,u_0,v_0 ax,ay,u0,v0 只与相机内部结构有关,因此称 M 1 \pmb M_1 M1 为相机的内参矩阵;而 M 2 \pmb M_2 M2 完全由相机相对于世界坐标系的方位决定,因此称为相机的外参矩阵;称 M \pmb M M 为投影矩阵。
三、相机标定
确定某一相机的内外参矩阵,称为相机标定。
将式 ( 6 ) (6) (6) 写成
Z c i [ u i v i 1 ] = [ m 11 m 12 m 13 m 14 m 21 m 22 m 23 m 24 m 31 m 32 m 33 m 34 ] [ X w i Y w i Z w i 1 ] (7) Z_{ci}\left[ \begin{matrix} u_i \\[2ex] v_i \\[2ex] 1 \end{matrix} \right]=\left[ \begin{matrix} m_{11} & m_{12} & m_{13} & m_{14} \\[2ex] m_{21} & m_{22} & m_{23} & m_{24} \\[2ex] m_{31} & m_{32} & m_{33} & m_{34} \end{matrix} \right]\left[ \begin{matrix} X_{wi} \\[2ex] Y_{wi} \\[2ex] Z_{wi} \\[2ex] 1 \end{matrix} \right]\tag{7} Zci uivi1 = m11m21m31m12m22m32m13m23m33m14m24m34 XwiYwiZwi1 (7)
其中, ( X w i , Y w i , Z w i , 1 ) (X_{wi},Y_{wi},Z_{wi},1) (Xwi,Ywi,Zwi,1) 为空间中第 i i i 个点的世界坐标; ( u i , v i , 1 ) (u_i,v_i,1) (ui,vi,1) 为对应的像素坐标。式 ( 7 ) (7) (7) 包含三个方程:
Z c i u i = m 11 X w i + m 12 Y w i + m 13 Z w i + m 14 Z c i v i = m 21 X w i + m 22 Y w i + m 23 Z w i + m 24 Z c i = m 31 X w i + m 32 Y w i + m 33 Z w i + m 34 (8) \begin{aligned} Z_{ci}u_i&=m_{11}X_{wi}+m_{12}Y_{wi}+m_{13}Z_{wi}+m_{14}\\[2ex] Z_{ci}v_i&=m_{21}X_{wi}+m_{22}Y_{wi}+m_{23}Z_{wi}+m_{24}\\[2ex] Z_{ci}&=m_{31}X_{wi}+m_{32}Y_{wi}+m_{33}Z_{wi}+m_{34} \end{aligned}\tag{8} ZciuiZciviZci=m11Xwi+m12Ywi+m13Zwi+m14=m21Xwi+m22Ywi+m23Zwi+m24=m31Xwi+m32Ywi+m33Zwi+m34(8)
将式 ( 8 ) (8) (8) 中的第一式减去 u i u_i ui 乘第三式,第二式减去 v i v_i vi 乘第三式,分别消去 Z c i Z_{ci} Zci 后,可得如下线性方程:
X w i m 11 + Y w i m 12 + Z w i m 13 + m 14 − u i X w i m 31 − u i Y w i m 32 − u i Z w i m 33 − u i m 34 = 0 X w i m 21 + Y w i m 22 + Z w i m 23 + m 24 − v i X w i m 31 − v i Y w i m 32 − v i Z w i m 33 − v i m 34 = 0 (9) \begin{aligned} X_{wi}m_{11}+Y_{wi}m_{12}+Z_{wi}m_{13}+m_{14}-u_iX_{wi}m_{31}-u_iY_{wi}m_{32}-u_iZ_{wi}m_{33}-u_im_{34}&=0\\[2ex] X_{wi}m_{21}+Y_{wi}m_{22}+Z_{wi}m_{23}+m_{24}-v_iX_{wi}m_{31}-v_iY_{wi}m_{32}-v_iZ_{wi}m_{33}-v_im_{34}&=0\\[2ex] \end{aligned}\tag{9} Xwim11+Ywim12+Zwim13+m14−uiXwim31−uiYwim32−uiZwim33−uim34Xwim21+Ywim22+Zwim23+m24−viXwim31−viYwim32−viZwim33−vim34=0=0(9)
上式表示,若已知 n n n 个点的世界坐标 ( X w i , Y w i , Z w i ) (X_{wi},Y_{wi},Z_{wi}) (Xwi,Ywi,Zwi),与它们的像素坐标 ( u i , v i ) (u_i,v_i) (ui,vi),则我们有 2 n 2n 2n 个关于投影矩阵 M \pmb M M 元素的线性方程。
由此可见,由空间6个以上点的世界坐标与对应的像素坐标,我们可求出投影矩阵 M \pmb M M。在一般的标定中,我们都有数十个已知点,使方程的个数远超未知数的个数,从而用最小二乘法求解以降低误差造成的影响。
相关文章:

计算机视觉——相机标定
计算机视觉——相机标定 一、像素坐标系、图像坐标系、相机坐标系、世界坐标系二、坐标系变换图像坐标系 → 像素坐标系相机坐标系 → 图像坐标系世界坐标系 → 相机坐标系 ⋆ \star ⋆ 世界坐标系 → 像素坐标系 三、相机标定 一、像素坐标系、图像坐标系、相机坐标系、世界坐…...

C语言中的数据类型(二)--结构体
在之前我们已经探讨了C语言中的自定义数据类型和数组,链接如下:C语言中的数据类型(上)_c语言数据类型-CSDN博客 目录 一、结构体的声明 二、结构体变量的定义和初始化 三、结构体成员的访问 3.1 结构体成员的直接访问 3.2 结…...

第1章:Neo4j简介与图数据库基础
1.1 图数据库概述 在当今数据爆炸的时代,数据不仅仅是以量取胜,更重要的是数据之间的关联关系。传统的关系型数据库在处理高度关联数据时往往力不从心,而图数据库则应运而生,成为处理复杂关联数据的理想选择。 传统关系型数据库…...

C++11:原子操作与内存顺序:从理论到实践的无锁并发实现
文章目录 0.简介1.并发编程需要保证的特性2.原子操作2.1 原子操作的特性 3.内存顺序3.1 顺序一致性3.2 释放-获取(Release-Acquire)3.3 宽松顺序(Relaxed)3.4 内存顺序 4.无锁并发5. 使用建议 0.简介 在并发编程中,原子性、可见性和有序性是…...

Android第十四次面试总结
OkHttp中获取数据与操作数据 一、数据获取核心机制 1. 同步请求(阻塞式) // 1. 创建HTTP客户端(全局应复用实例) OkHttpClient client new OkHttpClient();// 2. 构建请求对象(GET示例) Request r…...

动力电池点焊机:驱动电池焊接高效与可靠的核心力量|比斯特自动化
在新能源汽车与储能设备需求激增的背景下,动力电池的制造工艺直接影响产品性能与安全性。作为电芯与极耳连接的核心设备,点焊机如何平衡效率、精度与可靠性,成为电池企业关注的重点。 动力电池点焊机的核心功能是确保电芯与极耳的稳固连接。…...

【MySQL】10.事务管理
1. 事务的引入 首先我们需要知道CURD操作不加控制会产生什么问题: 为了解决上面的问题,CURD需要满足如下条件: 2. 事务的概念 事务就是一组DML语句组成,这些语句在逻辑上存在相关性,这一组DML语句要么全部成功&…...

Bugku-CTF-Web安全最佳刷题路线
曾经的我也是CTF六项全能,Web安全,密码学,杂项,Pwn,逆向,安卓样样都会。明明感觉这样很酷,却为何还是沦为社畜。Bugku-CTF-Web安全最佳刷题路线,我已经整理好了,干就完了…...
IT学习方法与资料分享
一、编程语言与核心技能:构建技术地基 1. 入门首选:Python 与 JavaScript Python:作为 AI 与数据科学的基石,可快速构建数据分析与自动化脚本开发能力。 JavaScript:Web 开发的核心语言,可系统掌握 React/V…...

程序代码篇---Python串口
在 Python 里,serial库(一般指pyserial)是串口通信的常用工具。下面为你介绍其常用的读取和发送操作函数及使用示例: 1. 初始化串口 要进行串口通信,首先得对串口对象进行初始化,代码如下: i…...
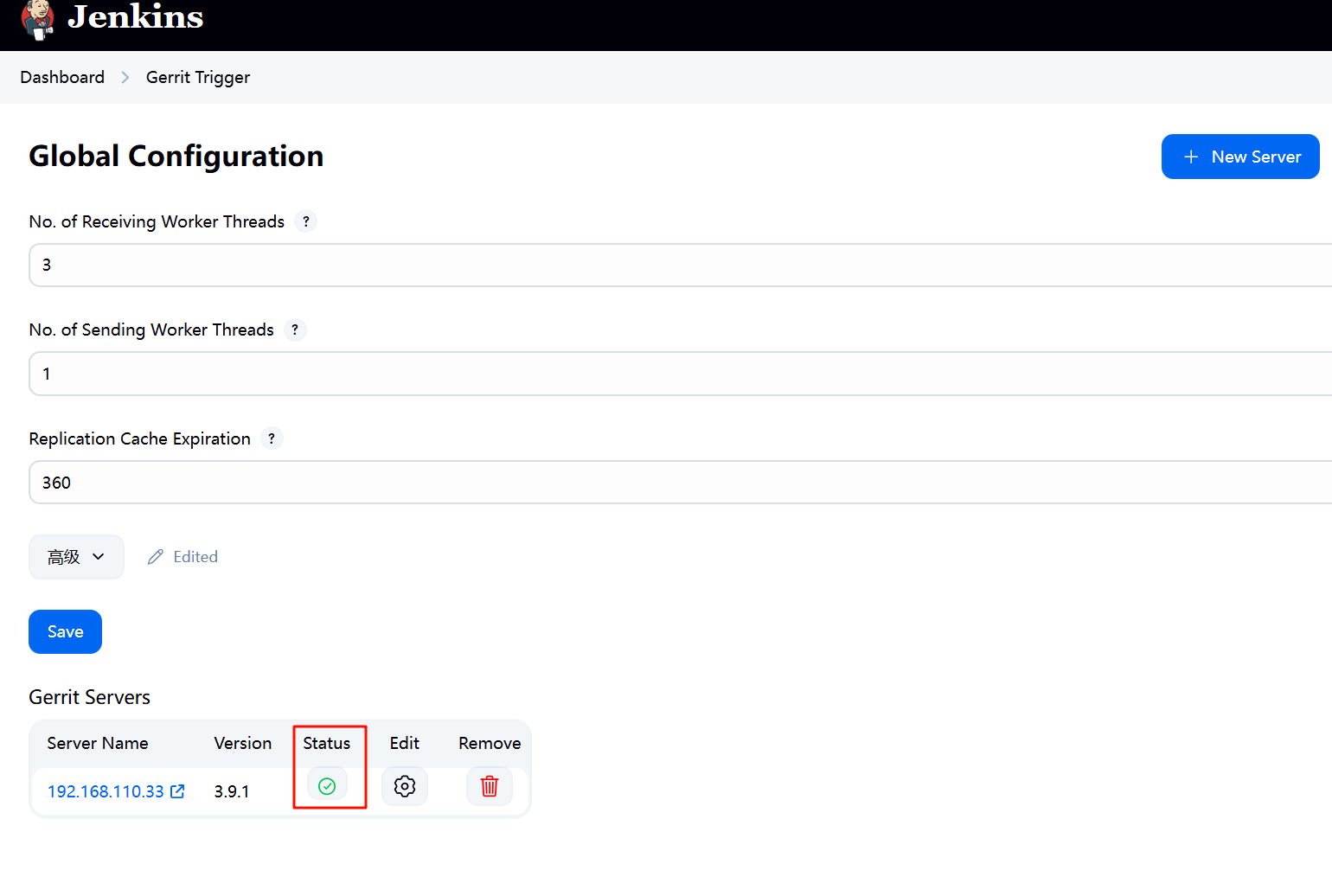
jenkins gerrit-trigger插件配置
插件gerrit-trigger下载好之后要在Manage Jenkins -->Gerrit Trigger-->New Server 中新增Gerrit Servers 配置好保存后点击“状态”查看是否正常...

虚拟主机都有哪些应用场景?
虚拟主机作为一种高效的网络托管方案,已经逐渐成为企业构建网站和应用软件的重要选择,下面,小编将为大家介绍一下虚拟主机的应用场景都有哪些吧! 虚拟主机可以帮助企业建立属于自己的企业网站,是用来展示公司形象和服务…...

预训练语言模型T5-11B的简要介绍
文章目录 模型基本信息架构特点性能表现应用场景 T5-11B 是谷歌提出的一种基于 Transformer 架构的预训练语言模型,属于 T5(Text-To-Text Transfer Transformer)模型系列,来自论文 Colin Raffel, Noam Shazeer, Adam Roberts, Kat…...

数论总结,(模版与题解)
数论 欧拉函数X质数(线性筛与二进制枚举)求解组合数欧拉降幂(乘积幂次)乘法逆元最小质因子之和模版 欧拉函数 欧拉函数的定义就是小于等于n的数里有f(n)个数与n互质,下面是求欧拉函数的模版。 package com.js.datas…...

EasyRTC嵌入式音视频通信SDK助力物联网/视频物联网音视频打造全场景应用
一、方案概述 随着物联网技术的飞速发展,视频物联网在各行业的应用日益广泛。实时音视频通信技术作为视频物联网的核心支撑,其性能直接影响着系统的交互体验和信息传递效率。EasyRTC作为一款成熟的音视频框架,具备低延迟、高画质、跨平台等…...
1-2 Linux-虚拟机(2025.6.7学习篇- win版本)
1、虚拟机 学习Linux系统,就需要有一个可用的Linux系统。 如何获得?将自己的电脑重装系统为Linux? NoNo。这不现实,因为Linux系统并不适合日常办公使用。 我们需要借助虚拟机来获得可用的Linux系统环境进行学习。 借助虚拟化技术&…...

Deepseek基座:Deepseek-v2核心内容解析
DeepSeek原创文章1 DeepSeek-v3:基于MLA的高效kv缓存压缩与位置编码优化技术 2 Deepseek基座:DeepSeek LLM核心内容解析 3 Deepseek基座:Deepseek MOE核心内容解析 4 Deepseek基座:Deepseek-v2核心内容解析 5Deepseek基座…...
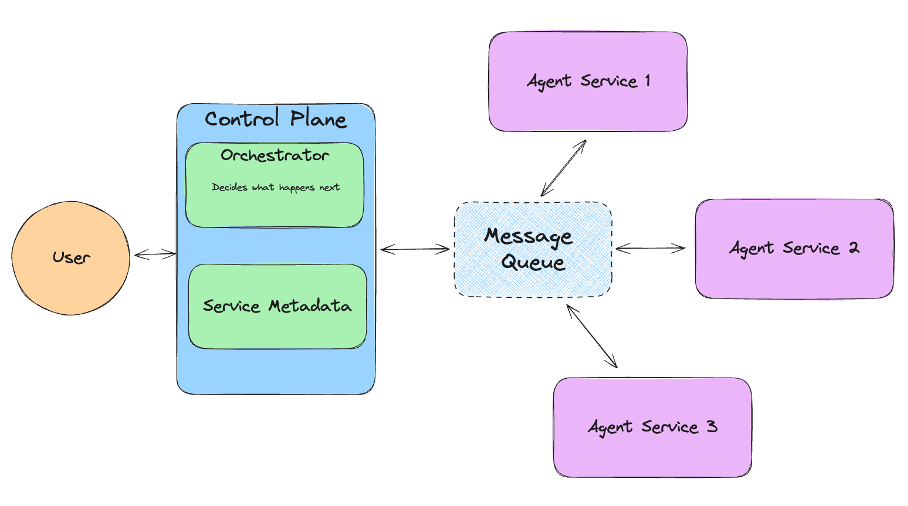
2025主流智能体Agent终极指南:Manus、OpenManus、MetaGPT、AutoGPT与CrewAI深度横评
当你的手机助手突然提醒"明天会议要带投影仪转接头",或是电商客服自动生成售后方案时,背后都是**智能体(Agent)**在悄悄打工。这个AI界的"瑞士军刀"具备三大核心特征: 自主决策能力:像老司机一样根据路况实时…...
家政小程序开发——AI+IoT技术融合,打造“智慧家政”新物种
基于用户历史订单(如“每周一次保洁”)、设备状态(如智能门锁记录的清洁频率),自动生成服务计划。 结合天气数据(如“雨天推荐玻璃清洁”),动态推送服务套餐。 IoT设备联动&#x…...

Keil开发STM32生成hex文件/bin文件
生成hex文件生成bin文件 STM32工程的hex文件和bin文件都可以通过Keil直接配置生成 生成hex文件 工程中点击魔术棒,在 Output 中勾选 Create HEX File 选项,OK保存工程配置 编译工程通过后可以看到编译输出窗口有创建hex文件的提示 默认可以在Output文…...

Windows 系统安装 Redis 详细教程
Windows 系统安装 Redis 详细教程 一、Redis 简介 Redis(Remote Dictionary Server)是一个开源的、基于内存的高性能键值存储系统,常被用作数据库、缓存和消息中间件。相比传统数据库,Redis 具有以下优势: 超高性能…...
)
“组件、路由懒加载”,在 Vue3 和 React 中分别如何实现? (copy)
Vue3 和 React 组件懒加载实现方式 React 中组件懒加载的实现方式 React 提供了 React.lazy 和 Suspense 两个 API 来实现组件的懒加载。React.lazy 用于动态导入组件,而 Suspense 则用于指定加载过程中的占位内容。例如,可以通过以下代码实现懒加载&a…...

.NET 事件模式举例介绍
.NET 事件模式:实现对象间松耦合通信 在软件开发中,对象之间的通信是一个常见且重要的问题。.NET 框架提供了一种标准化的事件模式,用于解决对象间的通信问题,实现松耦合的交互方式。今天,我们就通过一个简单的例子来…...

PDF 转 Markdown
本地可部署的模型 Marker Marker 快速准确地将文档转换为 markdown、JSON 和 HTML。 转换所有语言的 PDF、图像、PPTX、DOCX、XLSX、HTML、EPUB 文件在给定 JSON 架构 (beta) 的情况下进行结构化提取设置表格、表单、方程式、内联数学、链接、引用和代…...

北大开源音频编辑模型PlayDiffusion,可实现音频局部编辑,比传统 AR 模型的效率高出 50 倍!
北大开源了一个音频编辑模型PlayDiffusion,可以实现类似图片修复(inpaint)的局部编辑功能 - 只需修改音频中的特定片段,而无需重新生成整段音频。此外,它还是一个高性能的 TTS 系统,比传统 AR 模型的效率高出 50 倍。 自回归 Tra…...

蒲公英盒子连接问题debug
1、 现象描述 2、问题解决 上图为整体架构图,其中左边一套硬件设备是放在机房,右边是放在办公室。左边的局域网连接了可以访问外网的路由器,利用蒲公英作为旁路路由将局域网暴露在外网环境下。 我需要通过蒲公英作为旁路路由来进行远程访问&…...

Unity | AmplifyShaderEditor插件基础(第五集:简易膨胀shader)
一、👋🏻前言 大家好,我是菌菌巧乐兹~本节内容主要讲一下,如何用shader来膨胀~ 效果预览: 二、💨膨胀的基本原理 之前的移动是所有顶点朝着一个方向走,所以是移动 如果所有顶点照着自己的方…...

Django核心知识点全景解析
引言 本文深入剖析Django核心组件,涵盖数据交换、异步交互、状态管理及安全认证,附完整代码示例和避坑指南! 目录 引言 一、JSON:轻量级数据交换标准 1. 核心特性 2. 标准格式 3. 各语言处理方法 4. 常见错误示例 二、AJA…...

生物发酵展同期举办2025中国合成生物学与生物制造创新发展论坛
一、会议介绍 2025中国合成生物学与生物制造创新发展论坛暨上海国际合成生物学与生物制造展览会于2025年8月7-9日在上海新国际博览中心(浦东新区龙阳路2345号)召开,本次论坛汇聚了国内外顶尖学者、行业领袖及政策制定者,将围绕“…...

WINUI——Magewell视频捕捉开发手记
背景 因需要融合视频,并加载患者CT中提取出的气管镜与病变,以便能实时查看气管镜是否在正确位置。 开发环境 硬件:Magewell的USB Capture HDMI Gen 2 IDE:VS2022 FrameWork: .Net6 WINUI Package: MVVMToolKit NLog Ma…...
