Codeforces Round 1025 (Div. 2) B. Slice to Survive
Codeforces Round 1025 (Div. 2) B. Slice to Survive
题目
Duelists Mouf and Fouad enter the arena, which is an n × m n \times m n×m grid!
Fouad’s monster starts at cell ( a , b ) (a, b) (a,b), where rows are numbered 1 1 1 to n n n and columns 1 1 1 to m m m.
Mouf and Fouad will keep duelling until the grid consists of only one cell.
In each turn:
- Mouf first cuts the grid along a row or column line into two parts, discarding the part without Fouad’s monster. Note that the grid must have at least two cells; otherwise, the game has already ended.
- After that, in the same turn, Fouad moves his monster to any cell (possibly the same one it was in) within the remaining grid.
 Visualization of the phases of the fourth test case.
Visualization of the phases of the fourth test case.
Mouf wants to minimize the number of turns, while Fouad wants to maximize them. How many turns will this epic duel last if both play optimally?
Input
Each test contains multiple test cases. The first line contains the number of test cases t t t ( 1 ≤ t ≤ 10 4 1 \le t \le 10^4 1≤t≤104). The description of the test cases follows.
The first and only line of each test case contains four integers n n n, m m m, a a a, and b b b ( 2 ≤ n , m ≤ 10 9 2 \le n, m \le 10^9 2≤n,m≤109, 1 ≤ a ≤ n 1 \le a \le n 1≤a≤n, 1 ≤ b ≤ m 1 \le b \le m 1≤b≤m) — denoting the number of rows, the number of columns, the starting row of the monster, and the starting column of the monster, respectively.
Output
For each test case, output a single integer — the number of turns this epic duel will last if both play optimally.
Example
Input
8
2 2 1 1
3 3 2 2
2 7 1 4
2 7 2 2
8 9 4 6
9 9 5 5
2 20 2 11
22 99 20 70
Output
2
4
4
3
6
8
6
10
Note
In the first test case, one possible duel sequence is as follows:
- Turn 1: Mouf cuts the grid horizontally along the line between the rows 1 1 1 and 2 2 2, removing the bottom half and leaving a 1 × 2 1 \times 2 1×2 grid.
- Turn 1: Fouad’s monster is at the cell ( 1 , 1 ) (1,1) (1,1).
- Turn 2: Mouf cuts the 1 × 2 1 \times 2 1×2 grid again, removes one column, and isolates the cell ( 1 , 1 ) (1,1) (1,1).
The duel is completed in 2 2 2 turns.
In the fourth case, one possible duel sequence is as follows:
- Turn 1: Mouf cuts the grid vertically along the line between the columns 2 2 2 and 3 3 3, splitting it into a 2 × 2 2 \times 2 2×2 and a 2 × 5 2 \times 5 2×5 field, then removes the 2 × 5 2 \times 5 2×5 part.
- Turn 1: Fouad moves the monster to the cell ( 1 , 1 ) (1,1) (1,1).
- From this point on, the duel plays out just like the first test case—two more turns trim down the grid from 2 × 2 2 \times 2 2×2 to a single 1 × 1 1 \times 1 1×1 cell.
In total, the duel is completed in 3 3 3 turns.
You can refer to the pictures mentioned in the problem statement for illustrations of the fourth test case.
题目解析及思路
题目要求输出最终只剩一格的最小操作数
每轮操作由Mouf先执行,他可以对任意一行或一列切一刀
然后Fouad可以移动他的怪兽到任意一格
Mouf的最优操作是在切完以后给Fouad留下最少的格子
Fouad的最优操作是尽量移动到中间
代码
/*
因为最后一次操作是Mouf切完就结束
所以可以考虑先让Mouf切一次,然后再执行:先移动再切 的循环
Mouf的第一刀有四种情况
对于切完第一刀之后的循环,每次一定是长或宽变为原来的[n/2],可以直接算出次数
*/
#include <bits/stdc++.h>
#define int64 long long
#define endl '\n'
using namespace std;void solve(){int n,m,a,b;cin>>n>>m>>a>>b;int ans = n + m;vector<pair<int,int>> v;//第一刀的四种情况的长和宽v.push_back(make_pair(a,m));v.push_back(make_pair(n-a+1,m));v.push_back(make_pair(n,b));v.push_back(make_pair(n,m-b+1));for(auto [l,r] : v){int t = 0;//长和宽每次都是变为原来的[n/2]while(l > 1){t ++;l = (l + 1) / 2;}while(r > 1){t ++;r = (r + 1) / 2;}ans = min(ans,t);}//加上第一刀cout<<ans+1<<endl;
}
signed main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t;cin>>t;while(t--){solve();}
}
::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t;
cin>>t;
while(t--){solve();
}
}
相关文章:

Codeforces Round 1025 (Div. 2) B. Slice to Survive
Codeforces Round 1025 (Div. 2) B. Slice to Survive 题目 Duelists Mouf and Fouad enter the arena, which is an n m n \times m nm grid! Fouad’s monster starts at cell ( a , b ) (a, b) (a,b), where rows are numbered 1 1 1 to n n n and columns 1 1 1 t…...

ubuntu中使用docker
上一篇我已经下载了一个ubuntu:20.04的镜像; 1. 查看所有镜像 sudo docker images 2. 基于本地存在的ubuntu:20.04镜像创建一个容器,容器的名为cppubuntu-1。创建的时候就会启动容器。 sudo docker run -itd --name cppubuntu-1 ubuntu:20.04 结果出…...

复制与图片文件同名的标签文件到目标路径
引言:在数据集构建中,我们经常需要挑选一些特殊类型的图片(如:零件中有特殊脏污背景的图片,写论文的时候想单独对这类情况进行热力图验证)。我们把挑选出来的图片放到一个文件夹下,这时候我想快…...

【深度学习-Day 24】过拟合与欠拟合:深入解析模型泛化能力的核心挑战
Langchain系列文章目录 01-玩转LangChain:从模型调用到Prompt模板与输出解析的完整指南 02-玩转 LangChain Memory 模块:四种记忆类型详解及应用场景全覆盖 03-全面掌握 LangChain:从核心链条构建到动态任务分配的实战指南 04-玩转 LangChai…...

[ElasticSearch] DSL查询
🌸个人主页:https://blog.csdn.net/2301_80050796?spm1000.2115.3001.5343 🏵️热门专栏: 🧊 Java基本语法(97平均质量分)https://blog.csdn.net/2301_80050796/category_12615970.html?spm1001.2014.3001.5482 🍕 Collection与…...

iview中的table组件点击一行中的任意一点选中本行
<Table border ref"selection" size"small" on-row-click"onClickRow"></Table>// table组件点击一行任意位置选中onClickRow(row, index) {this.$refs.selection.toggleSelect(index)}写上toggleSelect(index)方法即可,…...

《探秘跨网段局域网IP广播:解锁网络通信的新姿势》
一、从基础出发:广播与跨网段 在计算机网络的世界中,广播域是一个至关重要的概念。简单来说,广播域是指网络中能接收任一台主机发出的广播帧的所有主机集合。当一台主机在广播域内发出一个广播帧时,同一广播域内的所有其他主机都可以收到该广播帧。在没有路由器或 VLAN 分割…...
)
Kafka 单机部署启动教程(适用于 Spark + Hadoop 环境)
🧭 Kafka 单机部署启动教程(适用于 Spark Hadoop 环境) 📦 一、Kafka 版本选择 推荐使用 Kafka 2.13-2.8.1(Scala 2.13,稳定适配 Spark 3.1.2 和 Hadoop 3.1.1) 下载地址(Apache 官…...
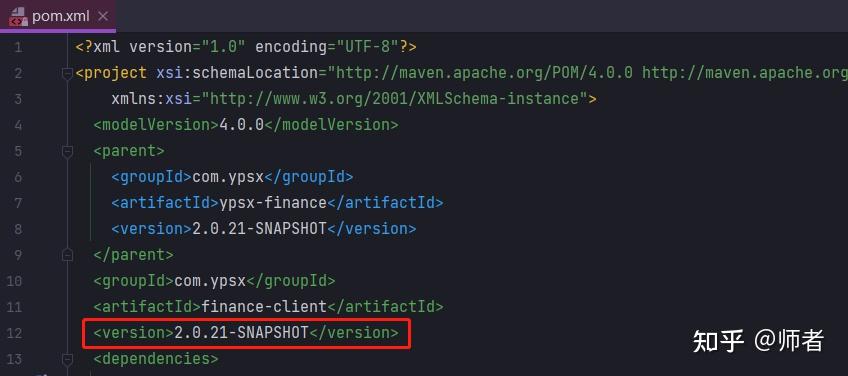
maven微服务${revision}依赖打包无法识别
1、场景描述 我现在又一个微服务项目,父pom的版本,使用<properties>定义好,如下所示: <name>ypsx-finance-center</name> <artifactId>ypsx-finance</artifactId> <packaging>pom</pack…...

2025年06月07日Github流行趋势
项目名称:netbird 项目地址url:https://github.com/netbirdio/netbird项目语言:Go历史star数:14824今日star数:320项目维护者:mlsmaycon, braginini, pascal-fischer, lixmal, pappz项目简介:使…...

WPS中将在线链接转为图片
WPS中将在线链接转为图片 文章目录 WPS中将在线链接转为图片一:解决方案1、下载图片,精确匹配(会员功能)2、将在线链接直接转为图片 一:解决方案 1、下载图片,精确匹配(会员功能) …...

实战二:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

二元函数可微 切平面逼近 线性函数逼近
二元函数 f ( x , y ) f(x, y) f(x,y) 在某点可微 的含义,可以从几何直观、严格数学定义、与一阶偏导数的关系三个层面来理解: 🔹1. 几何直观上的含义(最易理解) 二元函数 f ( x , y ) f(x, y) f(x,y) 在点 ( x 0 …...

vue生成二维码图片+文字说明
需求:点击下载图片,上方是二维码,下方显示该二维码的相关内容,并且居中显示,支持换行 解决方案步骤: 1. 使用qrcode生成二维码的DataURL。 2. 创建canvas,将二维码图片绘制到canvas的上半部分…...

机器学习监督学习实战五:六种算法对声呐回波信号进行分类
本项目基于UCI的声呐目标识别数据集(Sonar, Mines vs. Rocks),通过10种机器学习算法比较,发现集成学习方法表现最优。研究首先对60个声呐能量特征进行可视化分析(分布直方图、相关性矩阵),对比了…...

React Hooks 的闭包陷阱问题
这是主包在面试中遇到的一道题目,面试官的问题是:"这个页面初次展示出来时Count和step的值是什么,我点击按钮count和step的值有什么变化?“ 这个题目主包回答的不好,所以想做一个总结。 题目 import React, { …...

力扣面试150题--克隆图
Day 61 题目描述 思路 /* // Definition for a Node. class Node {public int val;public List<Node> neighbors;public Node() {val 0;neighbors new ArrayList<Node>();}public Node(int _val) {val _val;neighbors new ArrayList<Node>();}public N…...

【HarmonyOS 5】运动健康开发实践介绍以及详细案例
以下是 HarmonyOS 5 运动健康功能的简洁介绍,聚焦核心体验与技术亮点: 一、AI 驱动的全场景健康管理 智能运动私教:运动前推送热身指导,运动中实时纠正动作,运动后生成个性化报告与改进建议。AI 融合用户多设备数…...

STM32开发中,线程启动异常问题排查简述
1. 参数传递问题 错误类型:线程属性错误地使用。影响:线程属性(如堆栈大小、优先级)不匹配可能导致线程创建失败或行为异常。验证方法:检查 线程创建的返回值,若为 NULL 则表示线程创建失败。 2. 系统资源…...

SQL进阶之旅 Day 18:数据分区与查询性能
【SQL进阶之旅 Day 18】数据分区与查询性能 文章简述 在现代数据库系统中,随着数据量的快速增长,如何高效地管理和查询大规模数据成为开发人员和数据分析师面临的重要挑战。本文深入探讨了数据分区的概念及其对查询性能的提升作用,结合理论…...

鸿蒙PC,有什么缺点?
点击上方关注 “终端研发部” 设为“星标”,和你一起掌握更多数据库知识 价格太高,二是部分管理员权限首先,三对于开发者不太友好举个例子:VSCode的兼容性对程序员至关重要。若能支持VSCode,这台电脑将成为大多数开发者…...

前端工具:Webpack、Babel、Git与工程化流程
1. Webpack:资源打包优化工具 案例1:多入口文件打包 假设项目有多个页面(如首页index.js和登录页login.js),需要分别打包: ● 配置webpack.config.js: module.exports {entry: {index: ./sr…...

使用Python和Scikit-Learn实现机器学习模型调优
在机器学习项目中,模型的性能往往取决于多个因素,其中模型的超参数(hyperparameters)起着关键作用。超参数是模型在训练之前需要设置的参数,例如决策树的深度、KNN的邻居数等。合理地选择超参数可以显著提升模型的性能…...

灰狼优化算法MATLAB实现,包含种群初始化和29种基准函数测试
灰狼优化算法(Grey Wolf Optimizer, GWO)MATLAB实现,包含种群初始化和29种基准函数测试。代码包含详细注释和可视化模块: %% 灰狼优化算法主程序 (GWO.m) function GWO()clear; clc; close all;% 参数设置SearchAgents_no 30; …...

go语言学习 第7章:数组
第7章:数组 数组是一种基本的数据结构,用于存储相同类型的元素集合。在Go语言中,数组的大小是固定的,一旦定义,其长度不可改变。本章将详细介绍Go语言中数组的定义、初始化、访问、遍历以及一些常见的操作。 一、数组…...

PDF图片和表格等信息提取开源项目
文章目录 综合性工具专门的表格提取工具经典工具 综合性工具 PDF-Extract-Kit - opendatalab开发的综合工具包,包含布局检测、公式检测、公式识别和OCR功能 仓库:opendatalab/PDF-Extract-Kit特点:功能全面,包含表格内容提取的S…...

《Progressive Transformers for End-to-End Sign Language Production》复现报告
摘要 本文复现了《Progressive Transformers for End-to-End Sign Language Production》一文中的核心模型结构。该论文提出了一种端到端的手语生成方法,能够将自然语言文本映射为连续的 3D 骨架序列,并引入 Counter Decoding 实现动态序列长度控制。我…...

Haystack:AI与IoT领域的全能开源框架
一、Haystack 的定义与背景 Haystack 是一个开源框架,主要服务于两类不同领域: 物联网(IoT)与建筑自动化领域(Project Haystack): 旨在标准化物联网设备数据的语义模型,解决建筑系统(如 HVAC、能源管理)的数据互操作性问题,通过标签分类(Tagging Taxonomy)统一设…...

OpenWrt:使用ALSA实现边录边播
ALSA是Linux系统中的高级音频架构(Advanced Linux Sound Architecture)。目前已经成为了linux的主流音频体系结构,想了解更多的关于ALSA的知识,详见:http://www.alsa-project.org 在内核设备驱动层,ALSA提供…...

链表题解——回文链表【LeetCode】
算法思路 核心思想: 找到链表的中间节点。反转链表的后半部分。比较链表的前半部分和反转后的后半部分,如果值完全一致,则是回文链表。 具体步骤: 使用快慢指针找到链表的中间节点(middleNode 方法)。反转…...
