2023牛客暑期多校-J-Qu‘est-ce Que C‘est?(DP)
题意:
给定长度为n的数列,要求每个数都在
的范围,且任意长度大于等于2的区间和都大于等于0,问方案数。
。
思路:
首先要看出是dp题,用来表示遍历到第i位且后缀和最小为x的可行方案数(此时的后缀可以只有最后一位)。很显然j的值在区间
。下面考虑dp如何转换:
1.对于。 先讨论
,
可由
加一位值为
转换而来;也可由
加一位值为0 转换而来。就有
。再讨论
,可由
,加一位值为
转换而来;也可由
加一位值为1转换而来。就有
。依次讨论可以得出
可以由
,末位加值为
转换而来;也可由
,末位加x转换而来。综上所诉:
2.对于。可以去验证,只有
,末位加值为x才能转换成
。所以
。
为了方便计算我们把这个区间平移映射到
区间上。按照上述思想去找新的dp转换式就有:
由于都是求和到2m,所以可以考虑后缀和优化。
代码:
//#define _CRT_SECURE_NO_WARNINGS
//#include<iostream>
//#include<algorithm>
//#include<cstdio>
//#include<map>
//#include<string.h>
//#include<string>
//#include<vector>
//#include<__msvc_all_public_headers.hpp>
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll mod = 998244353;
const int N = 5005;
ll dp[N][N*2];//dp[i][j]表示遍历到i位,后缀和最小为j且合法的数量。(这里后缀和包含了只含有最后一位的情况)
ll sum[N * 2];//后缀数组
int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int n, m;cin >> n >> m;ll ans = 0;//初始化for (int i = 0; i <= m*2; i++){dp[1][i] = 1;}for (int i = 2; i <= n; i++){//处理后缀和for (int j = m * 2; j >= 0; j--)sum[j] = (sum[j + 1] + dp[i - 1][j]) % mod;//[0,m)的情况for (int j = 0; j < m; j++){dp[i][j] = sum[2 * m - j];}//[m,2m]的情况for (int j = m; j <= 2 * m; j++){dp[i][j] = sum[j - m];}}//统计for (int i = 0; i <= m * 2; i++){ans = (ans + dp[n][i]) % mod;}cout << ans << endl;return 0;
}
相关文章:
2023牛客暑期多校-J-Qu‘est-ce Que C‘est?(DP)
题意: 给定长度为n的数列,要求每个数都在的范围,且任意长度大于等于2的区间和都大于等于0,问方案数。。 思路: 首先要看出是dp题,用来表示遍历到第i位且后缀和最小为x的可行方案数(此时的后缀可以只有最…...
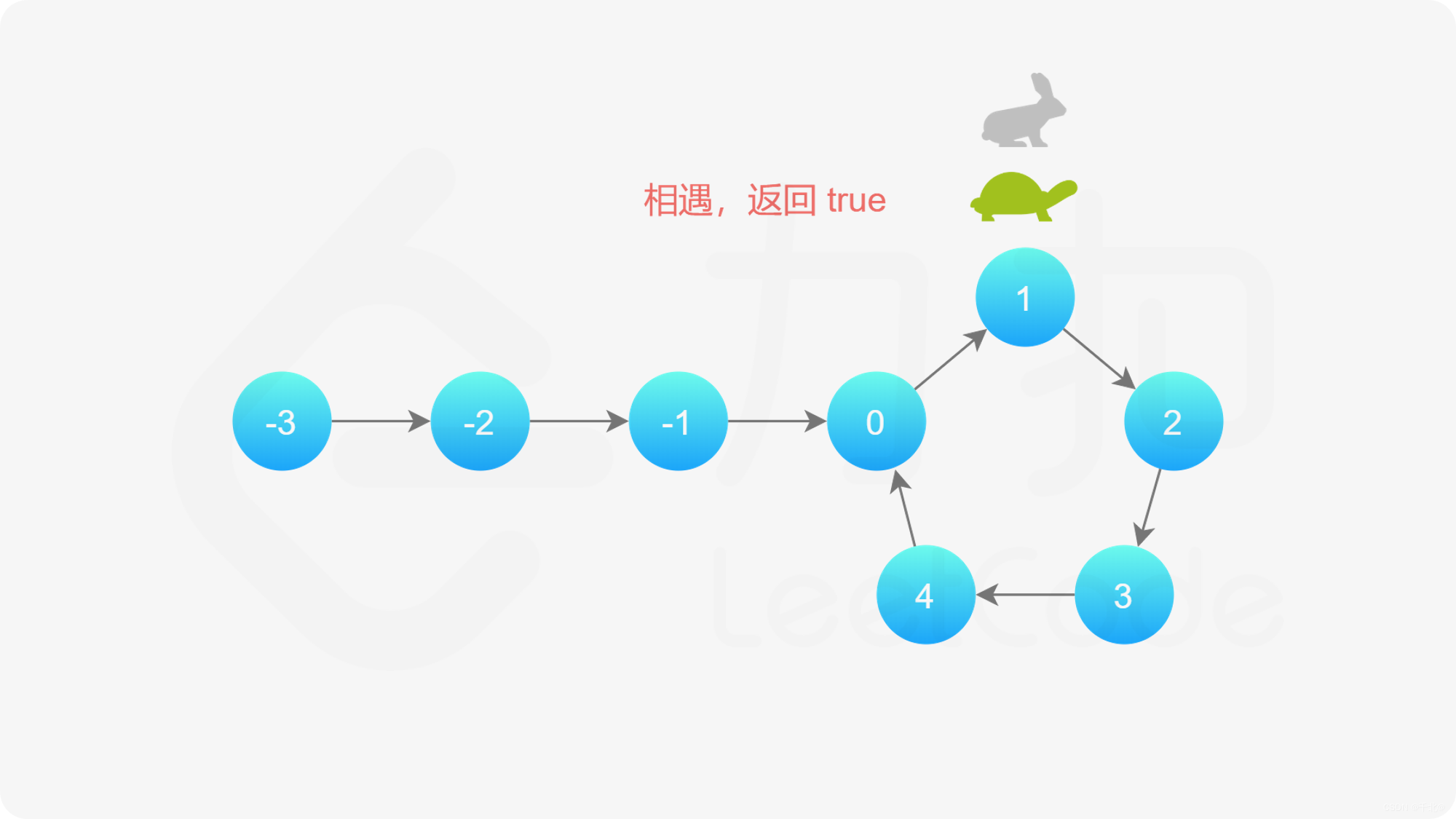
【141. 环形链表】
来源:力扣(LeetCode) 描述: 给你一个链表的头节点 head ,判断链表中是否有环。 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环&#x…...
ORB特征笔记
简介 ORB Oriented FAST Rotated BRIEF 前面的Oriented FAST说明的是它的关键点的选取是一种改良过的FAST,在FAST的基础上加了方向信息;后面的Rotated BRIEF是指特征描述符使用BRIEF描述子(Binary Robust Independent Elementary Featur…...
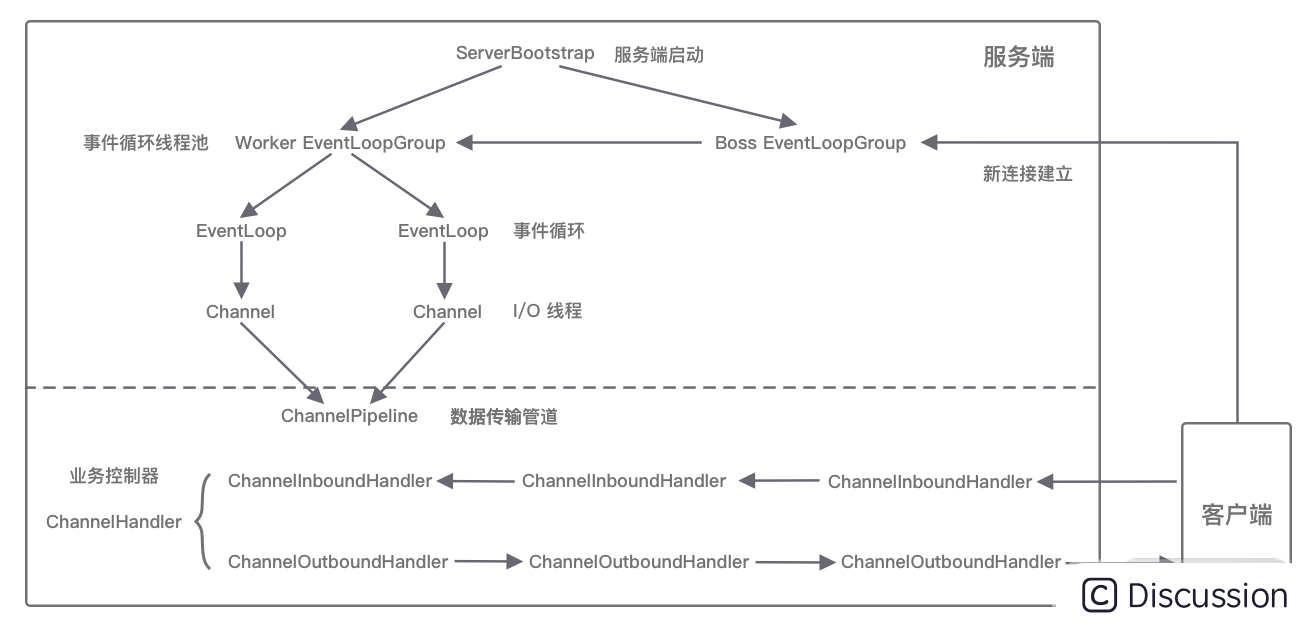
12.Netty源码之整体架构脉络
Netty 整体架构脉络 Netty 的逻辑处理架构为典型网络分层架构设计,共分为网络通信层、事件调度层、服务编排层,每一层各司其职。 网络通信层 网络通信层的职责是执行网络 I/O 的操作。它支持多种网络协议和 I/O 模型的连接操作。当网络数据读取到内核缓冲…...
【ArcGIS Pro二次开发】(54):三调名称转用地用海名称
三调地类和用地用海地类之间有点相似但并不一致。 在做规划时,拿到的三调,都需要将三调地类转换为用地用海地类,然后才能做后续的工作。 一般情况下,三调转用地用海存在【一对一,多对一和一对多】3种情况。 前2种情况…...

3D Tiles官方示例资源下载链接
本文列出Cesium官方提供的 3D Tiles 1.0和1.1规范的9个示例切块集(tileset)。 有关如何使用本地服务器托管这些示例的详细信息,请参阅 INSTRUCTIONS.md。 推荐:用 NSDT设计器 快速搭建可编程3D场景。 1、Metadata Granularities …...

【Java】分支结构习题
【Java】分支结构 文章目录 【Java】分支结构题1 :数字9 出现的次数题2 :计算1/1-1/21/3-1/41/5 …… 1/99 - 1/100 的值。题3 :猜数字题4 :牛客BC110 X图案题5 :输出一个整数的每一位题6 : 模拟三次密码输…...
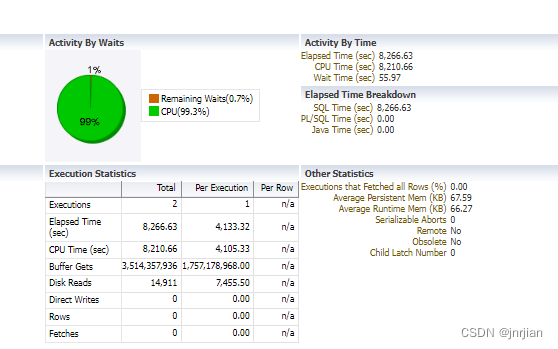
删除主表 子表外键没有索引的性能优化
整个表147M,执行时一个CPU耗尽, buffer gets 超过1个G, 启用并行也没有用 今天开发的同事问有个表上的数据为什么删不掉?我看了一下,也就不到100000条数据,表上有外键,等了5分钟hang在那里&…...

面向切面编程AOP
面向切面编程简介 IoC使软件组件松耦合。AOP让你能够捕捉系统中经常使用的功能,把它转化成组件。 AOP(Aspect Oriented Programming):面向切面编程,面向方面编程。(AOP是一种编程技术) AOP是对…...

大学生活题解
样例输入: 3 .xA ... Bx.样例输出: 6思路分析: 这道题只需要在正常的广搜模板上多维护一个— —方向,如果当前改变方向,就坐标不变,方向变,步数加一;否则坐标变,方向不…...

flask的配置项
flask的配置项 为了使 Flask 应用程序正常运行,有多种配置选项需要考虑。下面是一些基本的 Flask 配置选项: DEBUG: 这个配置项决定 Flask 是否应该在调试模式下运行。如果这个值被设为 True,Flask 将会提供更详细的错误信息,并…...

暑假刷题第16天--7/28
143. 最大异或对 - AcWing题库(字典树) #include<iostream> using namespace std; const int N100005; int a[N]; int nex[10000007][2],cnt; void insert(int x){int p0;for(int i30;i>0;i--){int ux>>i&1;if(!nex[p][u])nex[p][u]…...

vue vite ts electron ipc arm64
初始化 npm init vue # 全选 yes npm i # 进入项目目录后使用 npm install electron electron-builder -D npm install commander -D # 额外组件增加文件 新建 plugins 文件夹 src/background.ts 属于主进程 ipcMain.on、ipcMain.handle 都用于主进程监听 ipc,…...

数据分析-关于指标和指标体系
一、电商指标体系 二、指标体系的作用 三、统计学中基本的分析手段...

Vue+ElementUI操作确认框及提示框的使用
在进行数据增删改查操作中为保证用户的使用体验,通常需要显示相关操作的确认信息以及操作结果的通知信息。文章以数据的下载和删除提示为例进行了简要实现,点击下载以及删除按钮,会出现对相关信息的提示,操作结果如下所示。 点击…...

宋浩线性代数笔记(二)矩阵及其性质
更新线性代数第二章——矩阵,本章为线代学科最核心的一章,知识点多而杂碎,务必仔细学习。 重难点在于: 1.矩阵的乘法运算 2.逆矩阵、伴随矩阵的求解 3.矩阵的初等变换 4.矩阵的秩 (去年写的字,属实有点ugl…...

Linux之Shell 编程详解(二)
第 9 章 正则表达式入门 正则表达式使用单个字符串来描述、匹配一系列符合某个语法规则的字符串。在很多文 本编辑器里,正则表达式通常被用来检索、替换那些符合某个模式的文本。在 Linux 中,grep, sed,awk 等文本处理工具都支持…...
TCP网络通信编程之字节流
目录 【TCP字节流编程】 // 网络编程中,一定是server端先运行 【案例1】 【思路分析】 【客户端代码】 【服务端代码】 【结果展示】 【案例2】 【题目描述】 【注意事项】 【服务端代码】 【客户端代码】 【代码结果】 【TCP字节流编程】 // 网络编程中&a…...

【暑期每日一练】 day8
目录 选择题 (1) 解析: (2) 解析: (3) 解析: (4) 解析: (5) 解析: 编程题 题一 描述…...

maven的基本学习
maven https://www.bilibili.com/video/BV14j411S76G?p1&vd_source5c648979fd92a0f7ba8de0cde4f02a6e 1.简介 1.1介绍 Maven翻译为"专家"、“内行”,是Apache下的一个纯Java开发的开源项目。基于项目对象模型(缩写:POM)概念,Maven利用一…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...
