代码随想录算法训练营第二十五天 | 读PDF复习环节3
读PDF复习环节3
- 本博客的内容只是做一个大概的记录,整个PDF看下来,内容上是不如代码随想录网站上的文章全面的,并且PDF中有些地方的描述,是很让我疑惑的,在困扰我很久后,无意间发现,其网站上的讲解完全符合我的思路。这次看完这些PDF后,暂时一段时间内不会再看了,要复习还是依靠,代码随想录网站,视频,和我自己写的博客吧
- 回溯算法章节,这算是我掌握的还行的一个章节了。
- 组合
- 组合总和 III
- 电话号码的字母组合
- 组合总和
- 本题,代码随想录的剪枝策略是,排序之后加剪枝,可以,不符合条件直接跳出当层for循环了。
- 组合总和II
- 树层去重,used[i-1] = False 。树枝去重,used[i-1] = True .
- 分割回文串
- 复原IP地址
- 子集
- 求组合,就要用到 idx ,求排列,不需要 idx , 而且本题不需要 used 数组,idx 已经成功控制了。
- 子集II
- 递增子序列
- 本题太具有迷惑性了,一开始还真没注意!本题给的示例都是排好序的,让我误以为可以使用之前的去重逻辑!实则不然,因为求的是递增子序列,这意味着我们不能对数组进行排序操作,所以不能使用之前的去重逻辑。要使用新的,在递归函数中每次都声明的,哈希(集合)去重逻辑,我不喜欢用set,我喜欢用哈希。
- 代码随想录的代码
- 全排列
- 求排列,不需要 idx , 递归中每次都是从0开始遍历,但要用used数组,来表示哪些元素已经被使用过。
- 全排列 II
- 小小去重,可笑可笑
- 但是这道题的去重很有意思,要去看代码随想录的解答。
- 回溯算法去重问题的另一种写法
- 可以看看,核心思想是,讲解树层去重和树枝去重。
- 重新安排行程
- 再看依旧是不会
- N皇后
- 前几天写过了,核心思想就是,皇后一定是一行一行放的,每行放一个,所以可以用一个idx来控制当前是第几行,只要for循环遍历每个列位置就可以了,另外,在判断皇后是否合法时,我们只需要知道每个皇后的位置就可以了,不需要传入整个棋盘,那样太复杂了。
- 数独
- 本题的要点在于,就是在每个递归函数中,都使用三层,从0开始遍历的for循环,遍历行,遍历列,遍历数字,利用棋盘中,该位置是否是空,来判断是否在该位置填入数字,这样的编程逻辑是非常自然的。如果是想用idx来控制当前输入到了第几行第几列,那样就太麻烦了!遇到数字就continue,多跑几次什么都不做的for循环是无所谓的!
- 同样,在上面的编写逻辑下,判断是否合法也是较为容易的,只需要传入当前参数,每层循环的 i j k ,去判断,同行,同列,同小块,是否合法即可。
本博客的内容只是做一个大概的记录,整个PDF看下来,内容上是不如代码随想录网站上的文章全面的,并且PDF中有些地方的描述,是很让我疑惑的,在困扰我很久后,无意间发现,其网站上的讲解完全符合我的思路。这次看完这些PDF后,暂时一段时间内不会再看了,要复习还是依靠,代码随想录网站,视频,和我自己写的博客吧
回溯算法章节,这算是我掌握的还行的一个章节了。
组合
其中使用的剪枝技巧值得学习。

组合总和 III
class Solution:def combinationSum3(self, k: int, n: int) -> List[List[int]]:self.res = []path = []idx = 1self.backtracking(k,n,idx,path)return self.resdef backtracking(self,k,n,idx,path):if len(path)==k :if n == 0 :self.res.append(path.copy())returnelse :return# 小小剪枝for i in range(idx,10-(k-len(path))+1):# 小小剪枝if n-i < 0 :continueelse :path.append(i)self.backtracking(k,n-i,i+1,path)path.pop()return
电话号码的字母组合
只要用 idx 来控制当前应该取第几个数字,就只需要一层循环了,而不是之前我习惯的两层循环。
class Solution:def letterCombinations(self, digits: str) -> List[str]:if digits == '' :return []self.dict = {'1' : '', '0' : '' , '#' : '' , '*' : '' ,'2':'abc' , '3':'def' , '4':'ghi' , '5':'jkl', '6':'mno' ,'7':'pqrs','8':'tuv','9':'wxyz'}self.res = []path = []n = len(digits)idx = 0self.backtracking(digits,n,idx,path)return self.resdef backtracking(self,digits,n,idx,path):if len(path) == n :self.res.append(''.join(path))return# 取当前的数字number = digits[idx]ss = self.dict[number]m = len(ss)# 在当前数字对应的字符串中,从0开始遍历for i in range(m):path.append(ss[i])self.backtracking(digits,n,idx+1,path)path.pop()组合总和
本题需要注意的是,虽然元素可以重复,但是必须要有idx,idx是保证,遍历一直是正序的,不会走回头路。
class Solution:def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:self.res = []path = []n = len(candidates)idx = 0self.backtracking(candidates,n,target,idx,path)return self.resdef backtracking(self,candidates,n,target,idx,path):if target == 0 :self.res.append(path.copy())returnif target < 0 :returnfor i in range(idx,n):if target < candidates[i] :continuepath.append(candidates[i])# 注意这里,传入 idx 的区别,因为元素可以重复,所以是 i , 不是 i+1# 但是也必须要有idx !!! self.backtracking(candidates,n,target-candidates[i],i,path)path.pop()
本题,代码随想录的剪枝策略是,排序之后加剪枝,可以,不符合条件直接跳出当层for循环了。
class Solution:def backtracking(self, candidates, target, total, startIndex, path, result):if total == target:result.append(path[:])returnfor i in range(startIndex, len(candidates)):if total + candidates[i] > target:breaktotal += candidates[i]path.append(candidates[i])self.backtracking(candidates, target, total, i, path, result)total -= candidates[i]path.pop()def combinationSum(self, candidates, target):result = []candidates.sort() # 需要排序self.backtracking(candidates, target, 0, 0, [], result)return result
组合总和II
剪枝+used数组去重。
class Solution:def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:candidates.sort()n = len(candidates)self.res = []path = []used = [False]*nidx = 0self.backtracking(candidates,target,n,idx,path,used)return self.resdef backtracking(self,candidates,target,n,idx,path,used):if target == 0 :self.res.append(path.copy())returnif target < 0 :return for i in range(idx,n):if candidates[i] > target :breakif i > 0 and used[i-1] == False and candidates[i]==candidates[i-1]:continuepath.append(candidates[i])used[i] = Trueself.backtracking(candidates,target-candidates[i],n,i+1,path,used)used[i] = Falsepath.pop()
树层去重,used[i-1] = False 。树枝去重,used[i-1] = True .
代码随想录的代码
class Solution:def backtracking(self, candidates, target, total, startIndex, used, path, result):if total == target:result.append(path[:])returnfor i in range(startIndex, len(candidates)):# 对于相同的数字,只选择第一个未被使用的数字,跳过其他相同数字if i > startIndex and candidates[i] == candidates[i - 1] and not used[i - 1]:continueif total + candidates[i] > target:breaktotal += candidates[i]path.append(candidates[i])used[i] = Trueself.backtracking(candidates, target, total, i + 1, used, path, result)used[i] = Falsetotal -= candidates[i]path.pop()def combinationSum2(self, candidates, target):used = [False] * len(candidates)result = []candidates.sort()self.backtracking(candidates, target, 0, 0, used, [], result)return result分割回文串
注意分割区间定义即可,左闭右闭。
class Solution:def partition(self, s: str) -> List[List[str]]:self.res = []path = []n = len(s)idx = 0self.backtracking(s,n,idx,path)return self.resdef backtracking(self,s,n,idx,path):if idx >= n :self.res.append(path.copy())return # 这里注意细节就好,i就是要取到n-1# 加入s='aa',s[1:2]='a',索引下标,是不包括最后一个值的for i in range(idx,n):# 注意回文子串区间定义:[idx,i],i为分割线temp = s[idx:i+1]if self.is_right(temp):path.append(temp)self.backtracking(s,n,i+1,path)path.pop()def is_right(self,temp):left = 0right = len(temp)-1while left < right :if temp[left]!=temp[right]:return Falseleft += 1right -= 1 return True
还可以提前使用动态规划的方法,判断出给字符串的所有子串是否是回文串,然后将结果储存起来。核心代码就是,先从下到上遍历,再从左到右遍历,一共需要考虑三种情况,会导致 dp[i][j] 是回文串,dp[i][j] 代表字符串中 [i,j] 的子串,是不是回文串。
class Solution:def partition(self, s: str) -> List[List[str]]:result = []isPalindrome = [[False] * len(s) for _ in range(len(s))] # 初始化isPalindrome矩阵self.computePalindrome(s, isPalindrome)self.backtracking(s, 0, [], result, isPalindrome)return resultdef backtracking(self, s, startIndex, path, result, isPalindrome):if startIndex >= len(s):result.append(path[:])returnfor i in range(startIndex, len(s)):if isPalindrome[startIndex][i]: # 是回文子串substring = s[startIndex:i + 1]path.append(substring)self.backtracking(s, i + 1, path, result, isPalindrome) # 寻找i+1为起始位置的子串path.pop() # 回溯过程,弹出本次已经添加的子串def computePalindrome(self, s, isPalindrome):for i in range(len(s) - 1, -1, -1): # 需要倒序计算,保证在i行时,i+1行已经计算好了for j in range(i, len(s)):if j == i:isPalindrome[i][j] = Trueelif j - i == 1:isPalindrome[i][j] = (s[i] == s[j])else:isPalindrome[i][j] = (s[i] == s[j] and isPalindrome[i+1][j-1])复原IP地址
class Solution:def restoreIpAddresses(self, s: str) -> List[str]:self.res = []path = []idx = 0n = len(s)self.backtacking(s,n,idx,path)return self.resdef backtacking(self,s,n,idx,path):if idx >= n :if len(path)==4:self.res.append('.'.join(path))returnelse :returnif len(path)==3 :temp = s[idx:n]if self.is_right(temp):path.append(temp)self.backtacking(s,n,n,path)path.pop()else :for i in range(idx,n): temp = s[idx:i+1]if self.is_right(temp):path.append(temp)self.backtacking(s,n,i+1,path)path.pop()def is_right(self,temp):n = len(temp)if temp[0] == '0' and n > 1 :return Falseif int(temp) > 255 or int(temp) < 0 :return Falsereturn True
我觉得我还剪了一下枝,挺好,
代码随想录的代码:
class Solution:def restoreIpAddresses(self, s: str) -> List[str]:results = []self.backtracking(s, 0, [], results)return resultsdef backtracking(self, s, index, path, results):if index == len(s) and len(path) == 4:results.append('.'.join(path))returnif len(path) > 4: # 剪枝returnfor i in range(index, min(index + 3, len(s))):if self.is_valid(s, index, i):sub = s[index:i+1]path.append(sub)self.backtracking(s, i+1, path, results)path.pop()def is_valid(self, s, start, end):if start > end:return Falseif s[start] == '0' and start != end: # 0开头的数字不合法return Falsenum = int(s[start:end+1])return 0 <= num <= 255子集
冗余的代码,本题不需要 used 数组,idx 已经可以控制,不出现重复了。
class Solution:def subsets(self, nums: List[int]) -> List[List[int]]:self.res = []path = []n = len(nums)used = [False]*nidx = 0self.backtracking(nums,n,idx,used,path)return self.resdef backtracking(self,nums,n,idx,used,path):self.res.append(path.copy())# 本题还是要有idxfor i in range(idx,n):if used[i]==False :used[i]=Truepath.append(nums[i])self.backtracking(nums,n,i+1,used,path)path.pop()used[i]=False

求组合,就要用到 idx ,求排列,不需要 idx , 而且本题不需要 used 数组,idx 已经成功控制了。
代码随想录的代码:
class Solution:def subsets(self, nums):result = []path = []self.backtracking(nums, 0, path, result)return resultdef backtracking(self, nums, startIndex, path, result):result.append(path[:]) # 收集子集,要放在终止添加的上面,否则会漏掉自己# if startIndex >= len(nums): # 终止条件可以不加# returnfor i in range(startIndex, len(nums)):path.append(nums[i])self.backtracking(nums, i + 1, path, result)path.pop()
子集II
直接套用之前的去重逻辑。
class Solution:def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:self.res = []path = []nums.sort()n = len(nums)used = [False]*nidx = 0self.backtracking(nums,n,idx,used,path)return self.resdef backtracking(self,nums,n,idx,used,path):self.res.append(path.copy())# 本题还是要有idxfor i in range(idx,n):if i > 0 and used[i-1]==False and nums[i-1]==nums[i]:continueelse: used[i]=Truepath.append(nums[i])self.backtracking(nums,n,i+1,used,path)path.pop()used[i]=False
递增子序列
本题太具有迷惑性了,一开始还真没注意!本题给的示例都是排好序的,让我误以为可以使用之前的去重逻辑!实则不然,因为求的是递增子序列,这意味着我们不能对数组进行排序操作,所以不能使用之前的去重逻辑。要使用新的,在递归函数中每次都声明的,哈希(集合)去重逻辑,我不喜欢用set,我喜欢用哈希。
class Solution:def findSubsequences(self, nums: List[int]) -> List[List[int]]:self.res = []path = []idx = 0n = len(nums)self.backtracking(nums,n,idx,path)return self.resdef backtracking(self,nums,n,idx,path):if len(path)>=2:self.res.append(path.copy())used = [False]*201for i in range(idx,n):if used[100+nums[i]] == True:continueif path==[] or nums[i] >= path[-1] :path.append(nums[i])used[100+nums[i]] = Trueself.backtracking(nums,n,i+1,path)path.pop()
代码随想录的代码
递增子序列
class Solution:def findSubsequences(self, nums):result = []path = []self.backtracking(nums, 0, path, result)return resultdef backtracking(self, nums, startIndex, path, result):if len(path) > 1:result.append(path[:]) # 注意要使用切片将当前路径的副本加入结果集# 注意这里不要加return,要取树上的节点uset = set() # 使用集合对本层元素进行去重for i in range(startIndex, len(nums)):if (path and nums[i] < path[-1]) or nums[i] in uset:continueuset.add(nums[i]) # 记录这个元素在本层用过了,本层后面不能再用了path.append(nums[i])self.backtracking(nums, i + 1, path, result)path.pop()class Solution:def findSubsequences(self, nums):result = []path = []self.backtracking(nums, 0, path, result)return resultdef backtracking(self, nums, startIndex, path, result):if len(path) > 1:result.append(path[:]) # 注意要使用切片将当前路径的副本加入结果集used = [0] * 201 # 使用数组来进行去重操作,题目说数值范围[-100, 100]for i in range(startIndex, len(nums)):if (path and nums[i] < path[-1]) or used[nums[i] + 100] == 1:continue # 如果当前元素小于上一个元素,或者已经使用过当前元素,则跳过当前元素used[nums[i] + 100] = 1 # 标记当前元素已经使用过path.append(nums[i]) # 将当前元素加入当前递增子序列self.backtracking(nums, i + 1, path, result)path.pop()全排列
求排列,不需要 idx , 递归中每次都是从0开始遍历,但要用used数组,来表示哪些元素已经被使用过。
class Solution:def permute(self, nums: List[int]) -> List[List[int]]:self.res = []path = []n = len(nums)used = [False]*nself.backtracking(nums,n,used,path)return self.resdef backtracking(self,nums,n,used,path):if len(path)==n:self.res.append(path.copy())returnfor i in range(n):if used[i]==False :used[i]=Truepath.append(nums[i])self.backtracking(nums,n,used,path)path.pop()used[i]=False
全排列 II
小小去重,可笑可笑
lass Solution:def permuteUnique(self, nums: List[int]) -> List[List[int]]:self.res = []path = []n = len(nums)nums.sort()used = [False]*nself.backtracking(nums,n,used,path)return self.resdef backtracking(self,nums,n,used,path):if len(path)==n:self.res.append(path.copy())returnfor i in range(n):if i > 0 and used[i-1] == False and nums[i-1]==nums[i]:continueif used[i]==False:used[i]=Truepath.append(nums[i])self.backtracking(nums,n,used,path)path.pop()used[i]=False
但是这道题的去重很有意思,要去看代码随想录的解答。
全排列 II
回溯算法去重问题的另一种写法
可以看看,核心思想是,讲解树层去重和树枝去重。
回溯算法去重问题的另一种写法
重新安排行程
再看依旧是不会
重新安排行程
class Solution:def findItinerary(self, tickets: List[List[str]]) -> List[str]:tickets.sort() # 先排序,这样一旦找到第一个可行路径,一定是字母排序最小的used = [0] * len(tickets)path = ['JFK']results = []self.backtracking(tickets, used, path, 'JFK', results)return results[0]def backtracking(self, tickets, used, path, cur, results):if len(path) == len(tickets) + 1: # 终止条件:路径长度等于机票数量+1results.append(path[:]) # 将当前路径添加到结果列表return Truefor i, ticket in enumerate(tickets): # 遍历机票列表if ticket[0] == cur and used[i] == 0: # 找到起始机场为cur且未使用过的机票used[i] = 1 # 标记该机票为已使用path.append(ticket[1]) # 将到达机场添加到路径中state = self.backtracking(tickets, used, path, ticket[1], results) # 递归搜索path.pop() # 回溯,移除最后添加的到达机场used[i] = 0 # 标记该机票为未使用if state:return True # 只要找到一个可行路径就返回,不继续搜索
from collections import defaultdictclass Solution:def findItinerary(self, tickets: List[List[str]]) -> List[str]:targets = defaultdict(list) # 构建机场字典for ticket in tickets:targets[ticket[0]].append(ticket[1])for airport in targets:targets[airport].sort() # 对目的地列表进行排序path = ["JFK"] # 起始机场为"JFK"self.backtracking(targets, path, len(tickets))return pathdef backtracking(self, targets, path, ticketNum):if len(path) == ticketNum + 1:return True # 找到有效行程airport = path[-1] # 当前机场destinations = targets[airport] # 当前机场可以到达的目的地列表for i, dest in enumerate(destinations):targets[airport].pop(i) # 标记已使用的机票path.append(dest) # 添加目的地到路径if self.backtracking(targets, path, ticketNum):return True # 找到有效行程targets[airport].insert(i, dest) # 回溯,恢复机票path.pop() # 移除目的地return False # 没有找到有效行程
N皇后
前几天写过了,核心思想就是,皇后一定是一行一行放的,每行放一个,所以可以用一个idx来控制当前是第几行,只要for循环遍历每个列位置就可以了,另外,在判断皇后是否合法时,我们只需要知道每个皇后的位置就可以了,不需要传入整个棋盘,那样太复杂了。
代码随想录的代码:
class Solution:def solveNQueens(self, n: int) -> List[List[str]]:result = [] # 存储最终结果的二维字符串数组chessboard = ['.' * n for _ in range(n)] # 初始化棋盘self.backtracking(n, 0, chessboard, result) # 回溯求解return [[''.join(row) for row in solution] for solution in result] # 返回结果集def backtracking(self, n: int, row: int, chessboard: List[str], result: List[List[str]]) -> None:if row == n:result.append(chessboard[:]) # 棋盘填满,将当前解加入结果集returnfor col in range(n):if self.isValid(row, col, chessboard):chessboard[row] = chessboard[row][:col] + 'Q' + chessboard[row][col+1:] # 放置皇后self.backtracking(n, row + 1, chessboard, result) # 递归到下一行chessboard[row] = chessboard[row][:col] + '.' + chessboard[row][col+1:] # 回溯,撤销当前位置的皇后def isValid(self, row: int, col: int, chessboard: List[str]) -> bool:# 检查列for i in range(row):if chessboard[i][col] == 'Q':return False # 当前列已经存在皇后,不合法# 检查 45 度角是否有皇后i, j = row - 1, col - 1while i >= 0 and j >= 0:if chessboard[i][j] == 'Q':return False # 左上方向已经存在皇后,不合法i -= 1j -= 1# 检查 135 度角是否有皇后i, j = row - 1, col + 1while i >= 0 and j < len(chessboard):if chessboard[i][j] == 'Q':return False # 右上方向已经存在皇后,不合法i -= 1j += 1return True # 当前位置合法数独
本题的要点在于,就是在每个递归函数中,都使用三层,从0开始遍历的for循环,遍历行,遍历列,遍历数字,利用棋盘中,该位置是否是空,来判断是否在该位置填入数字,这样的编程逻辑是非常自然的。如果是想用idx来控制当前输入到了第几行第几列,那样就太麻烦了!遇到数字就continue,多跑几次什么都不做的for循环是无所谓的!
同样,在上面的编写逻辑下,判断是否合法也是较为容易的,只需要传入当前参数,每层循环的 i j k ,去判断,同行,同列,同小块,是否合法即可。
代码随想录的代码:
class Solution:def solveSudoku(self, board: List[List[str]]) -> None:"""Do not return anything, modify board in-place instead."""self.backtracking(board)def backtracking(self, board: List[List[str]]) -> bool:# 若有解,返回True;若无解,返回Falsefor i in range(len(board)): # 遍历行for j in range(len(board[0])): # 遍历列# 若空格内已有数字,跳过if board[i][j] != '.': continuefor k in range(1, 10):if self.is_valid(i, j, k, board):board[i][j] = str(k)if self.backtracking(board): return Trueboard[i][j] = '.'# 若数字1-9都不能成功填入空格,返回False无解return Falsereturn True # 有解def is_valid(self, row: int, col: int, val: int, board: List[List[str]]) -> bool:# 判断同一行是否冲突for i in range(9):if board[row][i] == str(val):return False# 判断同一列是否冲突for j in range(9):if board[j][col] == str(val):return False# 判断同一九宫格是否有冲突start_row = (row // 3) * 3start_col = (col // 3) * 3for i in range(start_row, start_row + 3):for j in range(start_col, start_col + 3):if board[i][j] == str(val):return Falsereturn True
相关文章:

代码随想录算法训练营第二十五天 | 读PDF复习环节3
读PDF复习环节3 本博客的内容只是做一个大概的记录,整个PDF看下来,内容上是不如代码随想录网站上的文章全面的,并且PDF中有些地方的描述,是很让我疑惑的,在困扰我很久后,无意间发现,其网站上的讲…...
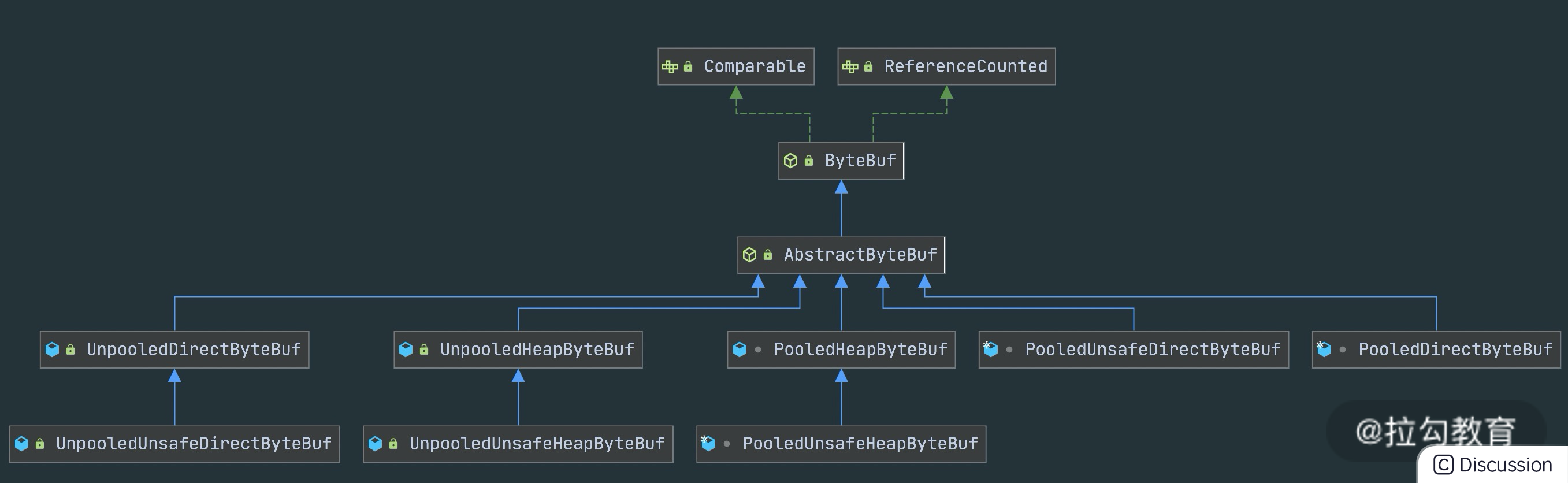
18.Netty源码之ByteBuf 详解
highlight: arduino-light ByteBuf 是 Netty 的数据容器,所有网络通信中字节流的传输都是通过 ByteBuf 完成的。 然而 JDK NIO 包中已经提供了类似的 ByteBuffer 类,为什么 Netty 还要去重复造轮子呢?本节课我会详细地讲解 ByteBuf。 JDK NIO…...
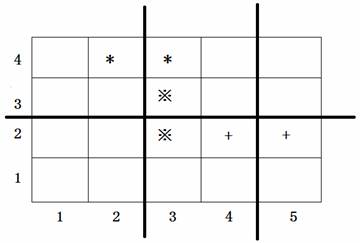
#P0999. [NOIP2008普及组] 排座椅
题目描述 上课的时候总会有一些同学和前后左右的人交头接耳,这是令小学班主任十分头疼的一件事情。不过,班主任小雪发现了一些有趣的现象,当同学们的座次确定下来之后,只有有限的 DD 对同学上课时会交头接耳。 同学们在教室中坐…...

Sentinel 容灾中心的使用
Sentinel 容灾中心的使用 往期文章 Nacos环境搭建Nacos注册中心的使用Nacos配置中心的使用 熔断/限流结果 Jar 生产者 spring-cloud-alibaba:2021.0.4.0 spring-boot:2.6.8 spring-cloud-loadbalancer:3.1.3 sentinel:2021.0…...

深度学习中简易FC和CNN搭建
TensorFlow是由谷歌开发的PyTorch是由Facebook人工智能研究院(Facebook AI Research)开发的 Torch和cuda版本的对应,手动安装较好 全连接FC(Batch*Num) 搭建建议网络: from torch import nnclass Mnist_NN(nn.Module):def __i…...

【多模态】20、OVR-CNN | 使用 caption 来实现开放词汇目标检测
文章目录 一、背景二、方法2.1 学习 视觉-语义 空间2.2 学习开放词汇目标检测 三、效果 论文:Open-Vocabulary Object Detection Using Captions 代码:https://github.com/alirezazareian/ovr-cnn 出处:CVPR2021 Oral 一、背景 目标检测数…...
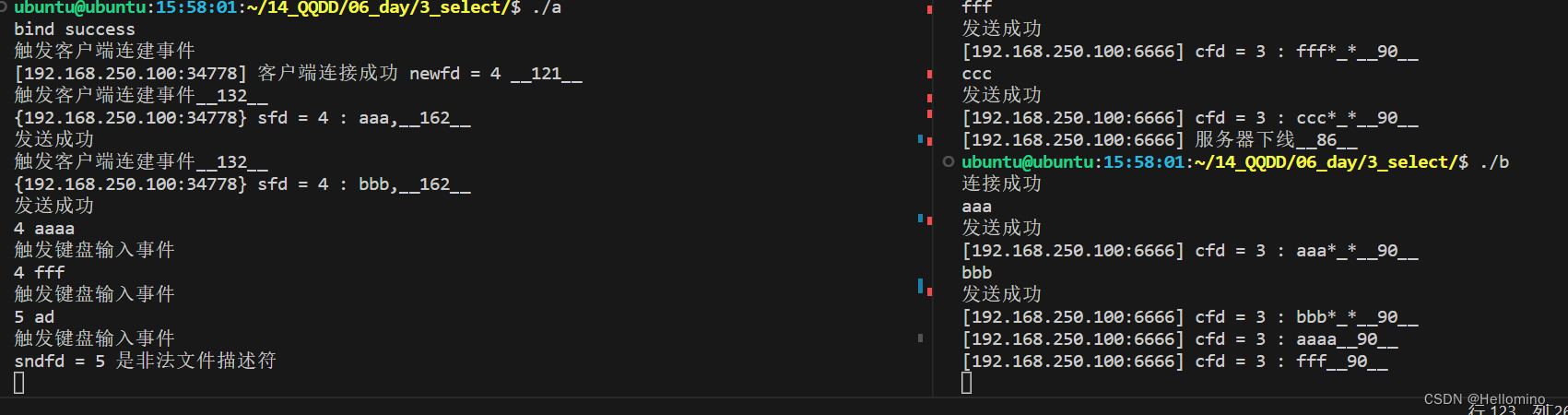
网络编程 IO多路复用 [select版] (TCP网络聊天室)
//head.h 头文件 //TcpGrpSer.c 服务器端 //TcpGrpUsr.c 客户端 select函数 功能:阻塞函数,让内核去监测集合中的文件描述符是否准备就绪,若准备就绪则解除阻塞。 原型: #include <sys/select.…...

数学建模学习(7):单目标和多目标规划
优化问题描述 优化 优化算法是指在满足一定条件下,在众多方案中或者参数中最优方案,或者参数值,以使得某个或者多个功能指标达到最优,或使得系统的某些性能指标达到最大值或者最小值 线性规划 线性规划是指目标函数和约束都是线性的情况 [x,fval]linprog(f,A,b,Aeq,Beq,LB,U…...

Element UI如何自定义样式
简介 Element UI是一套非常完善的前端组件库,但是如何个性化定制其中的组件样式呢?今天我们就来聊一聊这个 举例 就拿最常见的按钮el-button来举例,一般来说默认是蓝底白字。效果图如下 可是我们想个性化定制,让他成为粉底红字应…...

protobuf入门实践2
如何在proto中定义一个rpc服务? syntax "proto3"; //声明protobuf的版本package fixbug; //声明了代码所在的包 (对于C来说就是namespace)//下面的选项,表示生成service服务类和rpc方法描述, 默认是不生成的 option cc_generi…...

adb shell使用总结
文章目录 日志记录系统概览adb 使用方式 adb命令日志过滤按照告警等级进行过滤按照tag进行过滤根据告警等级和tag进行联合过滤屏蔽系统和其他App干扰,仅仅关注App自身日志 查看“当前页面”Activity文件传输截屏和录屏安装、卸载App启动activity其他 日志记录系统概…...
-Tag的含义、Tag类型与其他的转换)
UG NX二次开发(C++)-Tag的含义、Tag类型与其他的转换
文章目录 1、前言2、Tag号的含义3、tag_t转换为int3、TaggedObject与Tag转换3.1 TaggedObject定义3.2 TaggedObject获取Tag3.3 根据Tag获取TaggedObject4.Tag与double类型的转换1、前言 在UG NX中,每个对象对应一个tag号,C++中,其类型是tag_t,一般是5位或者6位的int数字,…...
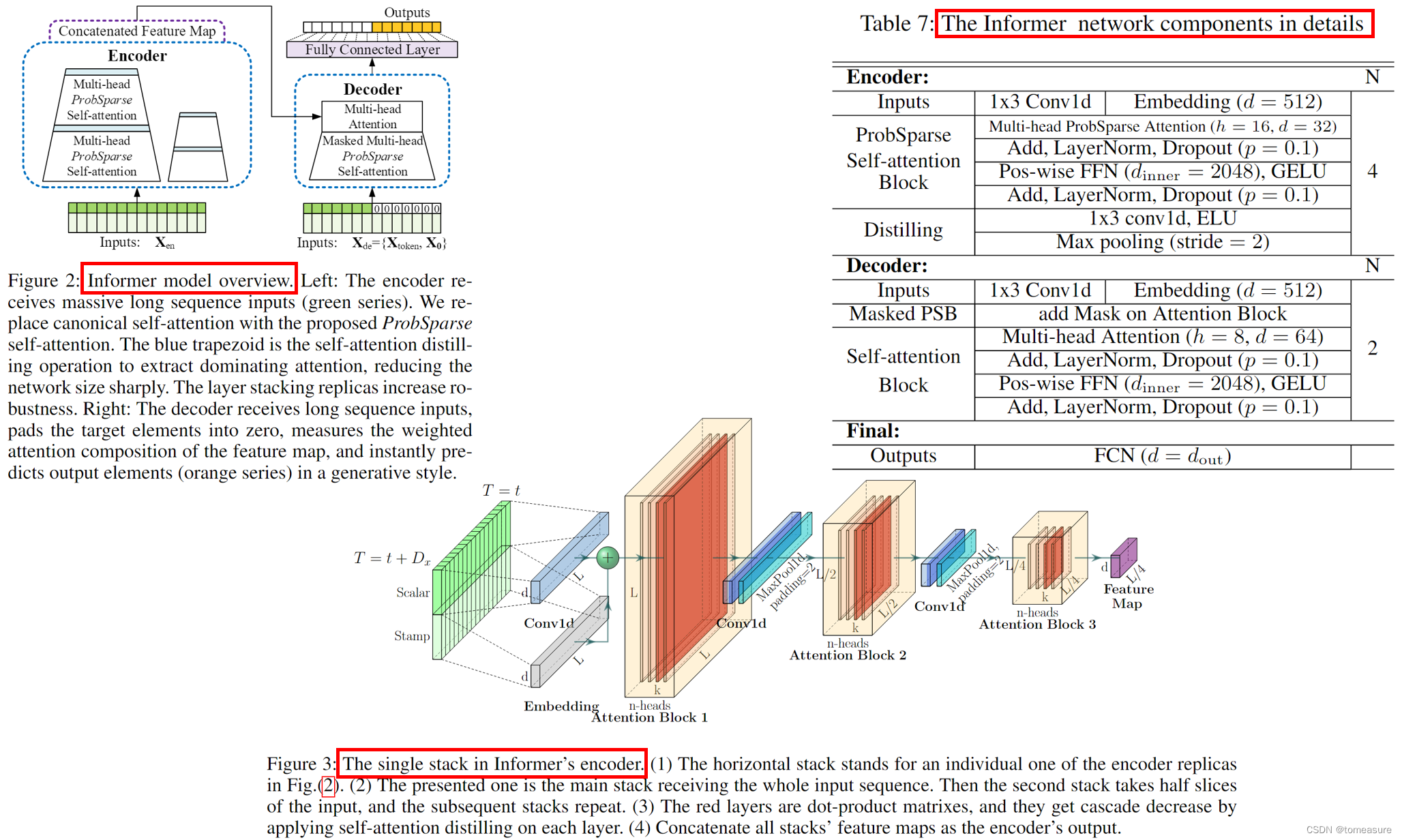
Informer 论文学习笔记
论文:《Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting》 代码:https://github.com/zhouhaoyi/Informer2020 地址:https://arxiv.org/abs/2012.07436v3 特点: 实现时间与空间复杂度为 O ( …...

c语言位段知识详解
本篇文章带来位段相关知识详细讲解! 如果您觉得文章不错,期待你的一键三连哦,你的鼓励是我创作的动力之源,让我们一起加油,一起奔跑,让我们顶峰相见!!! 目录 一.什么是…...
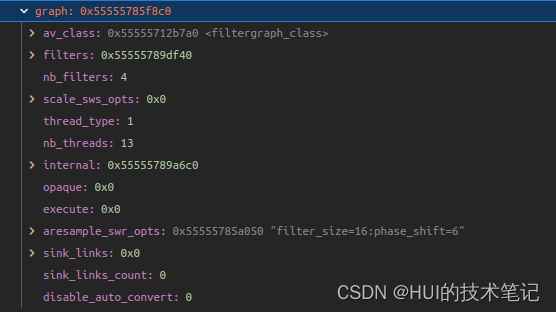
FFmpeg aresample_swr_opts的解析
ffmpeg option的解析 aresample_swr_opts是AVFilterGraph中的option。 static const AVOption filtergraph_options[] {{ "thread_type", "Allowed thread types", OFFSET(thread_type), AV_OPT_TYPE_FLAGS,{ .i64 AVFILTER_THREAD_SLICE }, 0, INT_MA…...

CAN学习笔记3:STM32 CAN控制器介绍
STM32 CAN控制器 1 概述 STM32 CAN控制器(bxCAN),支持CAN 2.0A 和 CAN 2.0B Active版本协议。CAN 2.0A 只能处理标准数据帧且扩展帧的内容会识别错误,而CAN 2.0B Active 可以处理标准数据帧和扩展数据帧。 2 bxCAN 特性 波特率…...

软工导论知识框架(二)结构化的需求分析
本章节涉及很多重要图表的制作,如ER图、数据流图、状态转换图、数据字典的书写等,对初学者来说比较生僻,本贴只介绍基础的轮廓,后面会有单独的帖子详解各图表如何绘制。 一.结构化的软件开发方法:结构化的分析、设计、…...

[SQL挖掘机] - 算术函数 - abs
介绍: 当谈到 SQL 中的 abs 函数时,它是一个用于计算数值的绝对值的函数。“abs” 代表 “absolute”(绝对),因此 abs 函数的作用是返回一个给定数值的非负值(即该数值的绝对值)。 abs 函数接受一个参数&a…...

vue拼接html点击事件不生效
vue使用ts,拼接html,点击事件不生效或者报 is not defined 点击事件要用onclick 不是click let data{name:测,id:123} let conHtml <div> "名称:" data.name "<br>" <p class"cursor blue&quo…...

【Spring】Spring之依赖注入源码解析
1 Spring注入方式 1.1 手动注入 xml中定义Bean,程序员手动给某个属性赋值。 set方式注入 <bean name"userService" class"com.firechou.service.UserService"><property name"orderService" ref"orderService"…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...
