秋招算法备战第28天 | 93.复原IP地址、78.子集、90.子集II
93. 复原 IP 地址 - 力扣(LeetCode)
这个问题可以通过深度优先搜索(DFS)的方法来解决。我们要做的就是在字符串的每个可能位置插入点,然后检查生成的每一部分是否在 0-255 的范围内,以及是否没有前导零(除非这一部分本身就是零)。以下是解决这个问题的 Python 代码示例。
def restoreIpAddresses(s):def dfs(s, part, path, res):if part == 4:if s == "":res.append(path[:-1])returnfor i in range(1, 4):if i <= len(s):if int(s[:i]) <= 255:dfs(s[i:], part + 1, path + s[:i] + ".", res)if s[0] == '0':breakres = []dfs(s, 0, "", res)return res# Test the function
s = "25525511135"
print(restoreIpAddresses(s))
上述代码的运行结果应该是 ['255.255.11.135', '255.255.111.35'],这是字符串 “25525511135” 可能形成的所有有效 IP 地址。
注意,以上代码默认你正在使用 Python 3.如果你正在使用其他语言,转换这段代码时需要保持算法的主体思想不变,但可能需要进行一些语法或者函数的调整。
下面是代码随想录的参考代码
class Solution:def restoreIpAddresses(self, s: str) -> List[str]:results = []self.backtracking(s, 0, [], results)return resultsdef backtracking(self, s, index, path, results):if index == len(s) and len(path) == 4:results.append('.'.join(path))returnif len(path) > 4: # 剪枝returnfor i in range(index, min(index + 3, len(s))):if self.is_valid(s, index, i):sub = s[index:i+1]path.append(sub)self.backtracking(s, i+1, path, results)path.pop()def is_valid(self, s, start, end):if start > end:return Falseif s[start] == '0' and start != end: # 0开头的数字不合法return Falsenum = int(s[start:end+1])return 0 <= num <= 255
78. 子集 - 力扣(LeetCode)
这是一个经典的回溯问题。基本思路是,从空子集开始,然后每次向子集中添加一个新的元素,创建一个新的子集,直到所有元素都被考虑过。对于包含n个元素的集合,其幂集包含2^n个元素,因为每个元素都可以在子集中出现或不出现。
在Python中,可以使用深度优先搜索的方式实现。下面是一个可能的解决方案:
def subsets(nums):def backtrack(first = 0, curr = []):# 如果当前组合达到了有效长度if len(curr) == k:output.append(curr[:])returnfor i in range(first, n):# 添加 nums[i] 进入当前组合curr.append(nums[i])# 使用下一个整数来完成组合backtrack(i + 1, curr)# 回溯,移除 nums[i] 从当前组合curr.pop()output = []n = len(nums)for k in range(n + 1):# 对于从0到n个数字的所有可能组合backtrack()return output
这个函数首先定义了一个递归的回溯函数,用于生成所有长度为k的可能组合。然后,函数为每个可能的组合长度(从0到n)调用了回溯函数。在回溯函数中,我们遍历nums中的所有元素,并在每一步中,都将当前元素添加到当前组合中,然后调用回溯函数来完成剩余的组合。最后,我们从当前组合中移除当前元素,以便在下一次迭代中尝试下一个元素。
90. 子集 II - 力扣(LeetCode)
这是一个带有重复元素的子集问题,它可以通过一种叫做"回溯法"的算法来解决。关键是需要在添加子集时检查这个子集是否已经在结果中了。
首先,为了方便比较,我们可以将输入数组排序。然后,我们使用递归函数backtrack来生成所有可能的子集。在backtrack中,我们添加当前的子集到结果中,然后对于当前位置之后的每一个元素,我们尝试把它添加到子集中,并递归调用backtrack。
这里是Python的实现:
def subsetsWithDup(nums):def backtrack(start, end, tmp):res.append(tmp[:])for i in range(start, end):if i > start and nums[i] == nums[i-1]: # 处理重复的元素continuetmp.append(nums[i])backtrack(i + 1, end, tmp)tmp.pop()nums.sort()res = []backtrack(0, len(nums), [])return res
在这个代码中,我们首先对nums进行排序,然后定义了回溯函数backtrack,最后调用了backtrack来生成所有的子集。在backtrack中,首先我们添加了当前的子集到结果中,然后从start位置开始,遍历到数组的末尾。对于每一个位置,我们首先检查是否有重复的元素,如果有就跳过。然后我们把当前元素加到当前的子集中,调用backtrack生成包含这个元素的所有子集,然后再把这个元素从子集中移除。通过这种方式,我们能够生成所有的子集,并且避免了重复的子集。
总结
Summary
🔍 93. 复原 IP 地址 - 力扣(LeetCode)
这个问题可以通过深度优先搜索(DFS)的方法来解决。我们要做的就是在字符串的每个可能位置插入点,然后检查生成的每一部分是否在 0-255 的范围内,以及是否没有前导零(除非这一部分本身就是零)。
🔍 78. 子集 - 力扣(LeetCode)
这是一个经典的回溯问题。基本思路是,从空子集开始,然后每次向子集中添加一个新的元素,创建一个新的子集,直到所有元素都被考虑过。对于包含n个元素的集合,其幂集包含2^n个元素,因为每个元素都可以在子集中出现或不出现。在Python中,可以使用深度优先搜索的方式实现。
🔍 90. 子集 II - 力扣(LeetCode)
这是一个带有重复元素的子集问题,它可以通过一种叫做"回溯法"的算法来解决。关键是需要在添加子集时检查这个子集是否已经在结果中了。首先,为了方便比较,我们可以将输入数组排序。然后,我们使用递归函数backtrack来生成所有可能的子集。
Facts
- [💻 Python] 使用深度优先搜索(DFS)的方法来解决复原 IP 地址问题,逐个位置插入点,检查生成的每一部分是否在 0-255 的范围内,且没有前导零(除非该部分本身就是零)。
- [💻 Python] 经典回溯问题,找出集合的所有子集。子集的幂集包含2^n个元素,每个元素可以在子集中出现或不出现。
- [💻 Python] 带有重复元素的子集问题,使用"回溯法"算法解决。需要检查添加的子集是否已经在结果中,可以通过排序数组来避免重复。
相关文章:

秋招算法备战第28天 | 93.复原IP地址、78.子集、90.子集II
93. 复原 IP 地址 - 力扣(LeetCode) 这个问题可以通过深度优先搜索(DFS)的方法来解决。我们要做的就是在字符串的每个可能位置插入点,然后检查生成的每一部分是否在 0-255 的范围内,以及是否没有前导零(除非这一部分本…...

Mongodb空间索引的使用以及与Django的对接
Mongodb的空间索引 Mongodb数据库大家都非常熟悉,是一个基于分布式文件存储的开源数据库系统,在高负载的情况下,添加更多的节点,可以保证服务器性能,数据结构由键值(key>value)对组成。MongoDB 文档类似于 JSON 对…...

Windows安装MySQL数据库
MySQL数据库安装 MySQL下载 下载地址:https://dev.mysql.com/downloads/mysql/ 可以选择下载msi或zip,以下为zip模式安装步骤 下载了mysql的zip安装包之后解压即可; Windows安装步骤 初始化MySQL,并记录生成的用户密码root的随机…...

聊聊函数式编程中的“式”
当谈到函数式编程的“式”时,通常指的是函数的组合、转换和应用,以及处理数据的方式和风格。在函数式编程中,式是用来构建程序逻辑的基本单元。 下面更详细解释函数式编程中的几个关键式: 函数的组合: 函数式编程中…...

ubuntu目录分析
在Ubuntu根目录下,以下是一些常见文件夹的含义: /bin:存放可执行文件,包含一些基本的命令和工具。 /boot:存放启动时所需的文件,如内核和引导加载程序。 /dev:包含设备文件,用于与硬…...

Python 进阶(三):正则表达式(re 模块)
❤️ 博客主页:水滴技术 🌸 订阅专栏:Python 入门核心技术 🚀 支持水滴:点赞👍 收藏⭐ 留言💬 文章目录 1. 导入re模块2. re模块中的常用函数2.1 re.search()2.2 re.findall()2.3 re.sub()2.4…...
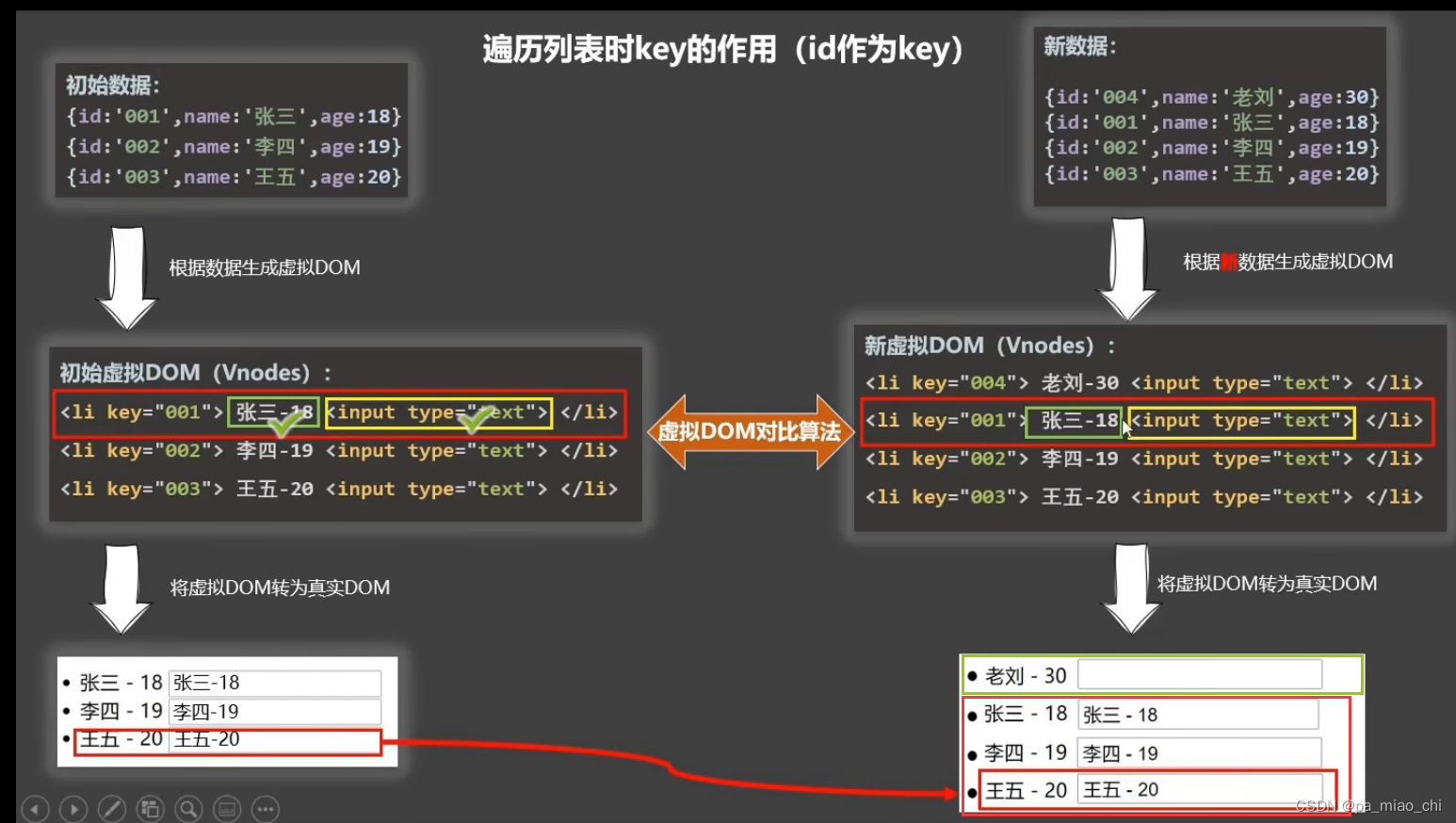
Vue2 第六节 key的作用与原理
(1)虚拟DOM (2)v-for中的key的作用 一.虚拟DOM 1.虚拟DOM就是内存中的数据 2.原生的JS没有虚拟DOM: 如果新的数据和原来的数据有重复数据,不会在原来的基础上新加数据,而是重新生成一份 3. Vue会有虚拟…...

React之组件的生命周期
React之组件的生命周期 一、概述二、整体说明三、挂载阶段四、更新阶段五、卸载阶段 一、概述 生命周期:一个事务从创建到最后消亡经历的整个过程组件的生命周期:组件从被创建到挂载到页面中运行,再到组件不用时卸载的过程意义:理解组件的生…...

linux -网络编程-多线程并发服务器
目录 1.三次握手和四次挥手 2 滑动窗口 3 函数封装思想 4 高并发服务器 学习目标: 掌握三次握手建立连接过程掌握四次握手关闭连接的过程掌握滑动窗口的概念掌握错误处理函数封装实现多进程并发服务器实现多线程并发服务器 1.三次握手和四次挥手 思考: 为什么…...

Golang之路---02 基础语法——字典
字典 字典(Map 类型),是由若干个 key:value 这样的键值对映射组合在一起的数据结构。 key 不能是切片,不能是字典,不能是函数。 字典初始化 方式:map[KEY_TYPE]VALUE_TYPE //1.var map1 map[string]int…...
)
Pytorch(三)
一、经典网络架构图像分类模型 数据预处理部分: 数据增强数据预处理DataLoader模块直接读取batch数据 网络模块设置: 加载预训练模型,torchvision中有很多经典网络架构,可以直接调用注意别人训练好的任务跟咱们的并不完全一样,需要把最后…...
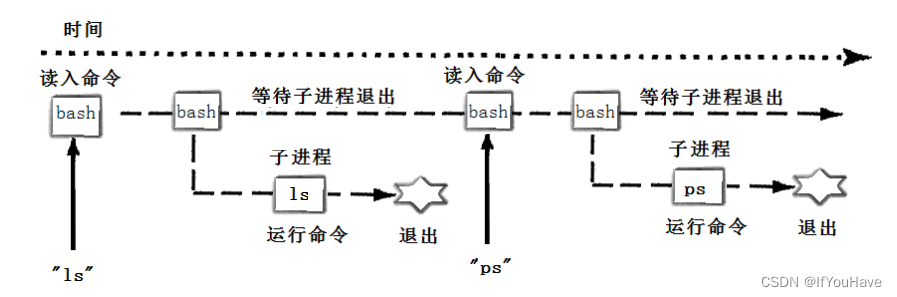
Linux——进程控制
目录 1. 进程创建 1.1 fork函数 1.2 fork系统调用内部宏观流程 1.3 fork后子进程执行位置分析 1.4 fork后共享代码分析 1.5 fork返回值 1.6 写时拷贝 1.7 fork常规用法 1.8 fork调用失败的原因 2.进程终止 2.1 进程退出场景 2.2 strerror函数—返回描述错误号的字符…...
)
剑指 Offer 59 - I. 滑动窗口的最大值 / LeetCode 239. 滑动窗口最大值(优先队列 / 单调队列)
题目: 链接:剑指 Offer 59 - I. 滑动窗口的最大值;LeetCode 239. 滑动窗口最大值 难度:困难 下一篇:剑指 Offer 59 - II. 队列的最大值(单调队列) 给你一个整数数组 nums,有一个大…...
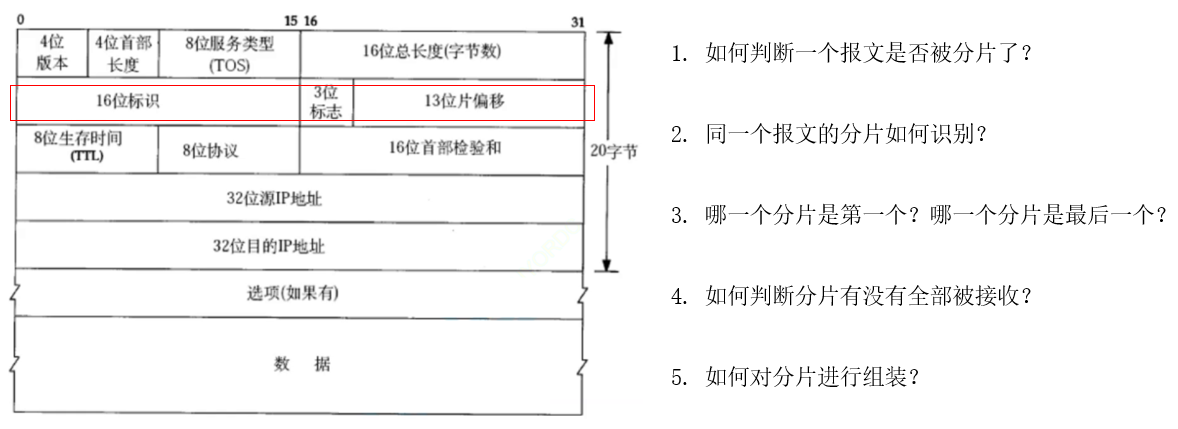
【Linux后端服务器开发】IP协议
目录 一、IP协议概述 二、协议头格式 三、网段划分 四、IP地址的数量限制 五、路由 六、分片和组装 一、IP协议概述 主机:配有IP地址,但是不进行路由控制的设备 路由器:即配有IP地址,又能进行路由控制 节点:主…...

React组件进阶之children属性,props校验与默认值以及静态属性static
React组件进阶之children属性,props校验与默认值以及静态属性static 一、children属性二、props校验2.1 props说明2.2 prop-types的安装2.3 props校验规则2.4 props默认值 三、静态属性static 一、children属性 children 属性:表示该组件的子节点,只要组…...
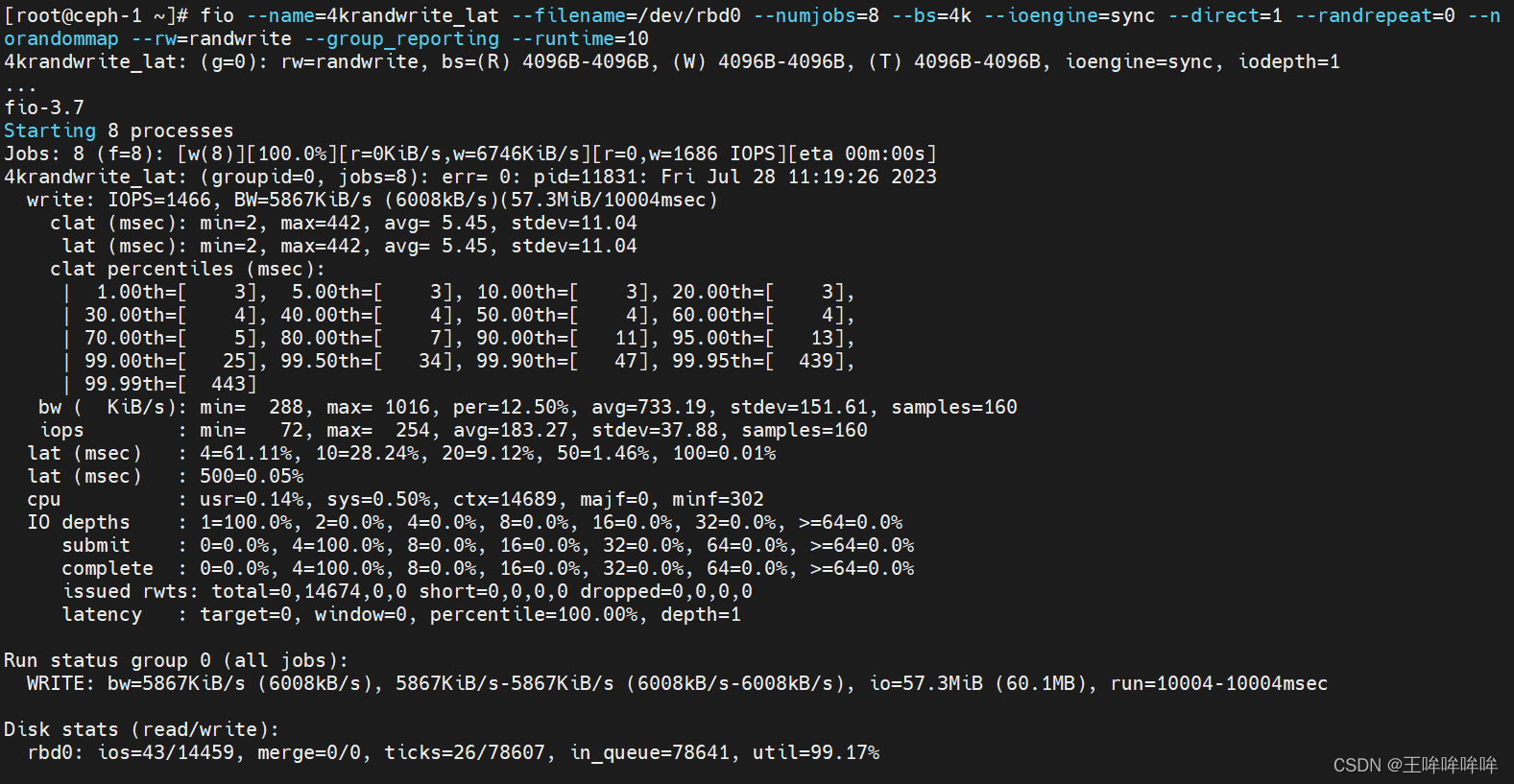
ceph集群中RBD的性能测试、性能调优
文章目录 rados benchrbd bench-write测试工具Fio测试ceph rbd块设备的iops性能测试ceph rbd块设备的带宽测试ceph rbd块设备的延迟 性能调优 rados bench 参考:https://blog.csdn.net/Micha_Lu/article/details/126490260 rados bench为ceph自带的基准测试工具&am…...

texshop mac中文版-TeXShop for Mac(Latex编辑预览工具)
texshop for mac是一款可以在苹果电脑MAC OS平台上使用的非常不错的Mac应用软件,texshop for mac是一个非常有用的工具,广泛使用在数学,计算机科学,物理学,经济学等领域的合作,这些程序的标准tetex分布特产…...
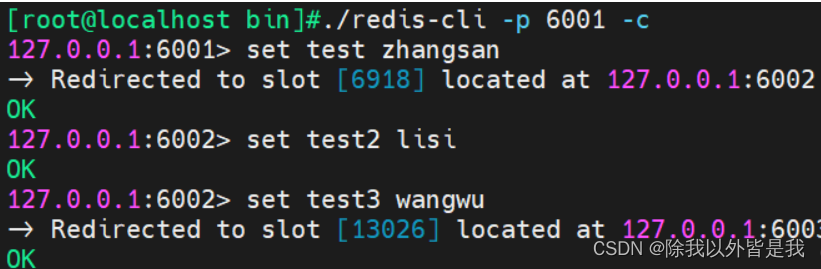
简单认识redis高可用实现方法
文章目录 一、redis群集三种模式二、 Redis 主从复制1、简介2、作用:3、流程:4.配置主从复制 三、Redis 哨兵模式1、简介2、原理:3、作用:4、哨兵结构由两部分组成,哨兵节点和数据节点:5、故障转移机制:6、…...

搭建git服务器
1.创建linux账户,创建文件 adduser git passwd gitpsw su git pwd cd ~/ mkdir .ssh cd ~/.ssh touch authorized_keys 2.特别重要(单独起一行),给文件设权限 chmod 700 /home/git/.ssh chmod 600 /home/git/.ssh/authorized_keys 3.本地生产密钥并把…...

线程中断机制
如何中断一个线程? 首先一个线程不应该由其他线程来强制中断或者停止,而是应该由线程自己自行停止。所以我们看到线程的stop()、resume()、suspend()等方法已经被标记为过时了。 其次在java中没有办法立即停止一个线程,然而停止线程显得尤为重…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...
 ----- Python的类与对象)
Python学习(8) ----- Python的类与对象
Python 中的类(Class)与对象(Object)是面向对象编程(OOP)的核心。我们可以通过“类是模板,对象是实例”来理解它们的关系。 🧱 一句话理解: 类就像“图纸”,对…...

Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...

渗透实战PortSwigger Labs指南:自定义标签XSS和SVG XSS利用
阻止除自定义标签之外的所有标签 先输入一些标签测试,说是全部标签都被禁了 除了自定义的 自定义<my-tag onmouseoveralert(xss)> <my-tag idx onfocusalert(document.cookie) tabindex1> onfocus 当元素获得焦点时(如通过点击或键盘导航&…...
