数学建模的32种常规方法及案例代码
比赛期间整理的数学建模的32种常规方法及案例代码友情分享:
链接:https://pan.baidu.com/s/18uDr1113a0jhd2No8O1Nog
提取码:xae5
在数学建模中,常规算法是指那些被广泛应用于各种问题求解的经典算法。这些算法覆盖了不同的数学和计算领域,包括优化、线性代数、图论、组合优化、数值计算等。以下介绍32种常规算法:
-
穷举法 (Exhaustive Search):通过尝试所有可能的解来寻找最优解,适用于问题规模较小的情况。
-
贪心算法 (Greedy Algorithm):每一步都选择当前看起来最优的解,局部最优解的选择可能不是全局最优解。
-
动态规划 (Dynamic Programming):将问题分解为子问题并保存子问题的解,避免重复计算,通常用于优化问题。
-
回溯算法 (Backtracking):通过试探和回溯来找出所有可能的解,适用于组合优化和排列组合问题。
-
分支界限法 (Branch and Bound):通过不断分割问题空间来寻找最优解,避免无效的搜索。
-
整数规划 (Integer Programming):在线性规划的基础上要求变量为整数,用于处理整数约束问题。
-
线性规划 (Linear Programming):求解线性约束下的目标函数最大或最小值,广泛应用于优化问题。
-
最小生成树算法 (Minimum Spanning Tree):在带权图中找出生成树,使权值之和最小。
-
最短路径算法 (Shortest Path):寻找图中两点之间的最短路径,常用算法包括 Dijkstra 和 Floyd-Warshall 等。
-
最大流算法 (Max-Flow Min-Cut):在有向图中找到从源点到汇点的最大流量路径。
-
拓扑排序 (Topological Sorting):将有向无环图(DAG)中的节点按顺序排列,保证所有边的方向一致。
-
图着色算法 (Graph Coloring):对图的节点进行染色,相邻节点颜色不相同。
-
背包问题算法 (Knapsack Problem):在给定背包容量和物品价值、重量情况下,选择装入背包使得总价值最大。
-
网络流算法 (Network Flow):寻找网络中最大流量和最小割的分配。
-
插值与拟合算法 (Interpolation and Curve Fitting):根据已知数据点推导出一个函数以逼近这些点。
-
数值积分算法 (Numerical Integration):通过数值方法计算函数在某个区间上的积分值。
-
方程求解算法 (Equation Solving):求解数学方程的解,常用算法包括二分法和牛顿法等。
-
近似算法 (Approximation Algorithm):用于求解 NP 难问题的近似解。
-
目标规划 (Goal Programming):优化问题中同时考虑多个目标函数的算法。
-
蒙特卡洛方法 (Monte Carlo Method):通过随机抽样和统计模拟来解决问题。
-
调度算法 (Scheduling):对任务进行合理的排列和分配,以达到最优的效果。
-
稀疏矩阵算法 (Sparse Matrix):针对具有大量零元素的矩阵进行高效的计算。
-
傅里叶变换 (Fourier Transform):将信号从时间域转换到频率域,用于信号处理和图像处理等。
-
插值算法 (Interpolation):通过已知数据点推导出一个函数以逼近这些点。
-
随机优化算法 (Random Optimization):通过随机搜索来优化问题的解。
-
数值微分算法 (Numerical Differentiation):通过数值方法计算函数的导数值。
-
整数分拆算法 (Integer Partition):将一个正整数拆分为若干个正整数之和。
-
谱方法 (Spectral Methods):通过傅里叶级数或其他谱展开方法进行数值求解。
-
最大团算法 (Maximum Clique):在无向图中寻找最大的完全子图(团)。
-
近似求解算法 (Approximation Methods):用于求解复杂问题的近似解。
-
松弛算法 (Relaxation Methods):用于求解线性方程组和非线性方程组的迭代算法。
-
凸优化算法 (Convex Optimization):用于求解凸优化问题的方法,保证全局最优解。
数学建模涉及众多经典算法和方法,下面列举一些常见的数学建模经典算法,并提供简单的案例代码作为示例。这些案例代码仅供参考,实际应用中可能需要根据具体问题进行调整和优化。
- 线性回归算法:
线性回归是一种用于拟合线性模型的算法,用于建立因变量与自变量之间的关系。下面是一个简单的线性回归案例代码:
import numpy as np
from sklearn.linear_model import LinearRegression# 示例数据
X = np.array([[1], [2], [3], [4], [5]])
y = np.array([2, 4, 5, 4, 5])# 创建线性回归模型
model = LinearRegression()# 拟合数据
model.fit(X, y)# 预测
prediction = model.predict([[6]])print("预测结果:", prediction)
2.线性规划算法:
线性规划是求解目标函数为线性的最优化问题。下面是一个简单的线性规划案例代码:
from scipy.optimize import linprog# 线性规划示例
c = [-1, 2] # 目标函数系数
A = [[-3, 1], [1, 2]] # 不等式约束系数
b = [-3, 5] # 不等式约束右侧常数
x_bounds = (0, None) # x取值范围# 求解线性规划
result = linprog(c, A_ub=A, b_ub=b, bounds=[x_bounds, x_bounds])print("最优解:", result.x)
print("最优值:", -result.fun)
3.TSP(旅行商问题)算法:
TSP是经典的组合优化问题,要求找到最短的回路,使得旅行商访问所有城市并返回起始城市。下面是一个简单的TSP算法示例:
import numpy as np
from itertools import permutations# 示例数据
distances = np.array([[0, 10, 15, 20],[10, 0, 35, 25],[15, 35, 0, 30],[20, 25, 30, 0]
])# 求解TSP
min_distance = float('inf')
optimal_path = Nonefor path in permutations(range(len(distances))):total_distance = 0for i in range(len(path) - 1):total_distance += distances[path[i]][path[i + 1]]total_distance += distances[path[-1]][path[0]]if total_distance < min_distance:min_distance = total_distanceoptimal_path = pathprint("最短距离:", min_distance)
print("最优路径:", optimal_path)
4.蒙特卡洛
蒙特卡洛方法是一种基于随机采样的数值计算方法,用于求解复杂问题或进行概率统计。下面将给出一个蒙特卡洛方法的案例和简单代码实现。
案例:计算圆的面积
我们可以通过蒙特卡洛方法来估计圆的面积。考虑一个边长为2的正方形,将一个单位圆完全包含在该正方形内。我们可以在该正方形内随机产生大量的点,然后计算这些点中有多少落在圆的内部。根据概率统计,我们可以利用落在圆内的点数与总点数的比例来估计圆的面积。
import randomdef monte_carlo_circle_area(num_points):inside_circle = 0for _ in range(num_points):x = random.uniform(-1, 1)y = random.uniform(-1, 1)distance = x**2 + y**2if distance <= 1:inside_circle += 1square_area = 4 # 正方形的面积circle_area = (inside_circle / num_points) * square_areareturn circle_areanum_points = 100000 # 采样点数
estimated_area = monte_carlo_circle_area(num_points)
print("估计的圆的面积:", estimated_area)
5.插值算法
插值算法是用于估计数据点之间未知数据点的一种方法。它通过已知数据点的函数值来推断未知数据点的函数值,从而实现数据的光滑逼近。以下是一个常见的插值算法——拉格朗日插值法的案例和代码实现。
案例:给定一组离散数据点,利用拉格朗日插值法估计中间位置的函数值。
def lagrange_interpolation(x_known, y_known, x):# 计算拉格朗日插值多项式的系数n = len(x_known)result = 0.0for i in range(n):term = y_known[i]for j in range(n):if i != j:term *= (x - x_known[j]) / (x_known[i] - x_known[j])result += termreturn result# 示例数据
x_known = [1, 2, 4, 7]
y_known = [3, 5, 9, 8]# 插值点
x_interp = 3# 使用拉格朗日插值法计算插值点的函数值
y_interp = lagrange_interpolation(x_known, y_known, x_interp)print("插值点 ({}, {}) 的函数值为: {}".format(x_interp, y_interp))
在这个案例中,我们给定了一组离散的数据点 (x_known, y_known),我们要求在中间位置 x_interp 处进行插值,估计其对应的函数值 y_interp。拉格朗日插值法利用多项式来逼近数据点,求得插值点的函数值。请注意,拉格朗日插值法是一种简单且直观的插值算法,但在处理大量数据点时,可能会引起龙格现象,导致插值结果不稳定。对于大规模数据集,其他插值方法(如样条插值)可能更合适。
以上提供的代码只是对相应算法的简单实现,实际数学建模中可能需要根据具体问题的特点进行更复杂的处理。数学建模中经典算法的应用取决于问题的具体需求和复杂程度。
学习数学建模中的32种常规算法需要一定的时间和努力,但通过有条理的学习和实践,可以掌握这些算法。以下是学习数学建模常规算法的一些建议:
-
掌握基本数学知识:数学建模涉及到多个数学领域,如线性代数、微积分、概率论、图论等。首先,确保您掌握了这些基础数学知识。
-
学习算法原理:对于每种算法,学习其原理和基本思想是非常重要的。了解算法的工作原理和适用范围,以及算法的优缺点。
-
查阅资料:有关数学建模和算法的书籍、教程和学术论文等资料是很好的学习资源。查阅相关资料,深入了解每种算法的细节和实际应用。
-
学习实例:通过解决实际问题的案例学习,可以帮助您更好地理解算法的应用。尝试模仿并理解实例中的算法过程。
-
编程实践:使用编程语言实现这些算法是非常有益的。通过编程实践,您可以加深对算法的理解,同时掌握实际应用中的技巧。
-
解决问题:挑战自己解决实际问题。将所学的算法应用到实际情况中,解决数学建模问题,这将提高您的算法应用能力。
-
学习工具:了解和学习相关的数学建模工具和软件。这些工具可以帮助您更快速、更高效地实现算法。
-
参与竞赛:参与数学建模竞赛是锻炼和应用所学算法的好机会。竞赛中常常涉及多种算法,参与竞赛可以提高算法解决问题的能力。
-
与他人讨论:与其他对数学建模感兴趣的人讨论学习和应用算法的经验和问题,可以互相学习和进步。
-
坚持实践:学习数学建模和算法需要时间和实践。坚持不懈地学习和实践,不断积累经验和技巧。
最重要的是,学习数学建模和常规算法需要持续的学习和实践。不要期望一蹴而就,保持积极的学习态度,持续不断地提升自己的能力。
相关文章:

数学建模的32种常规方法及案例代码
比赛期间整理的数学建模的32种常规方法及案例代码友情分享: 链接:https://pan.baidu.com/s/18uDr1113a0jhd2No8O1Nog 提取码:xae5 在数学建模中,常规算法是指那些被广泛应用于各种问题求解的经典算法。这些算法覆盖了不同的数学…...
【Django+Vue】英文成绩管理平台--20230727
能够满足大部分核心需求(标绿):报表部分应该比较难。 项目地址 前端编译 https://gitlab.com/m7840/toeic_vue_dist Vue源码 https://gitlab.com/m7840/toeic_vue Django源码 https://gitlab.com/m7840/toeic_python 项目架构 流程 …...

栈-模拟栈
实现一个栈,栈初始为空,支持四种操作: push x – 向栈顶插入一个数 x; pop – 从栈顶弹出一个数; empty – 判断栈是否为空; query – 查询栈顶元素。 现在要对栈进行 M 个操作,其中的每个…...

图观| 从王宝强、费翔、阿汤哥等新上映的电影聊聊图的智能推荐场景
从技术的视角来看,推荐系统本质上是在用户需求不明确的情况下,从海量的信息中为用户过滤出他可能感兴趣的信息的一种技术手段。 我们日常接触到的智能推荐有: 电商网站:如淘宝、天猫、京东、Amazon…… 生活服务:如美…...
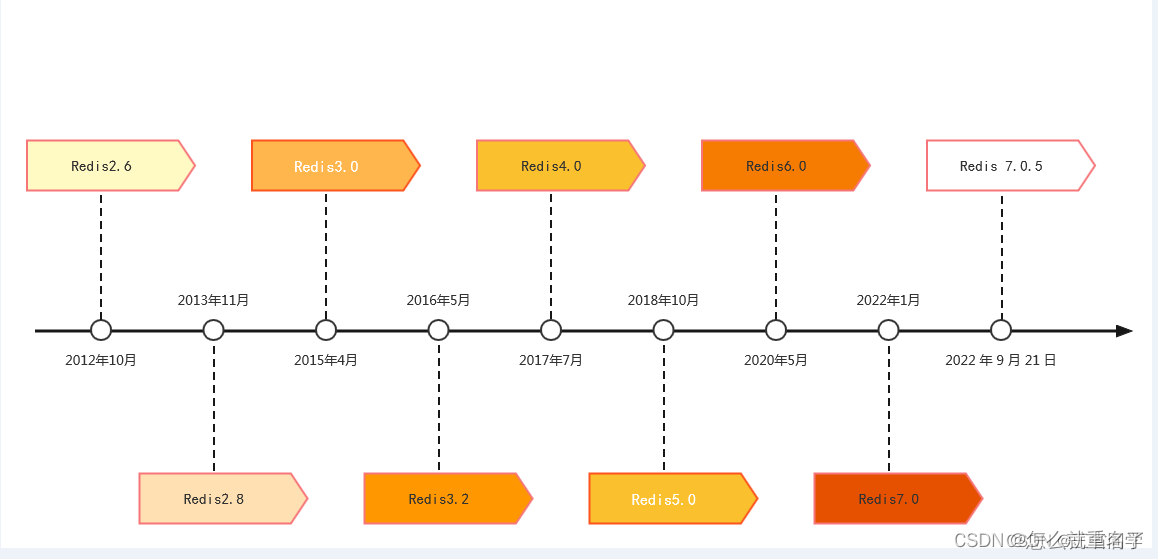
Redis系列一:介绍
介绍 The open source, in-memory data store used by millions of developers as a database, cache, streaming engine, and message broker. 相关资源 Redis 官网:https://redis.io/ 源码地址:https://github.com/redis/redis Redis 在线测试&#…...

Java 设计模式 - 单例模式 - 保证类只有一个实例
单例模式 - 保证类只有一个实例 为什么使用单例模式?单例模式的实现方式1. 饿汉式(Eager Initialization)2. 懒汉式(Lazy Initialization)3. 双重检查锁(Double-Checked Locking)4. 静态内部类&…...

第2章 JavaScript语法
准备工作 编写js需要准备一个编译器和游览器,js必须通过HTML/XHTML文档编写 js的编写位置 <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Docume…...

【Golang】Golang进阶系列教程--为什么 Go for-range 的 value 值地址每次都一样?
文章目录 前言现象无限循环相同地址 原因推荐阅读 前言 循环语句是一种常用的控制结构,在 Go 语言中,除了 for 关键字以外,还有一个 range 关键字,可以使用 for-range 循环迭代数组、切片、字符串、map 和 channel 这些数据类型。…...
)
小研究 - JVM 垃圾回收方式性能研究(三)
本文从几种JVM垃圾回收方式及原理出发,研究了在 SPEC jbb2015基准测试中不同垃圾回收方式对于JVM 性能的影响,并通过最终测试数据对比,给出了不同应用场景下如何选择垃圾回收策略的方法。 目录 4 垃圾回收器性能比较 4.1 测试结果 5 结语 …...

java根据poi解析excel内容
一.HSSFWorkbook、XSSFWorkbook、SXSSFWorkbook Apache POI包中的HSSFWorkbook、XSSFWorkbook、SXSSFWorkbook的区别如下: HSSFWorkbook:一般用于操作Excel2003以前(包括2003)的版本,扩展名是.xls。 XSSFWorkbook:一…...

实验报告-Sublime配置默认语法,以配置Verilog语法为例
实验报告-Sublime配置默认语法,以配置Verilog语法为例 1,下载Verilog语法环境2,Sublime配置语法工作环境,以Verilog语法环境为例。3,打开一个新的Sublime,验证编辑器配置Verilog为默认语法成功!4,Sublime汉化1,下载Verilog语法环境 参考文献: 1,Sublime Text 4加载…...
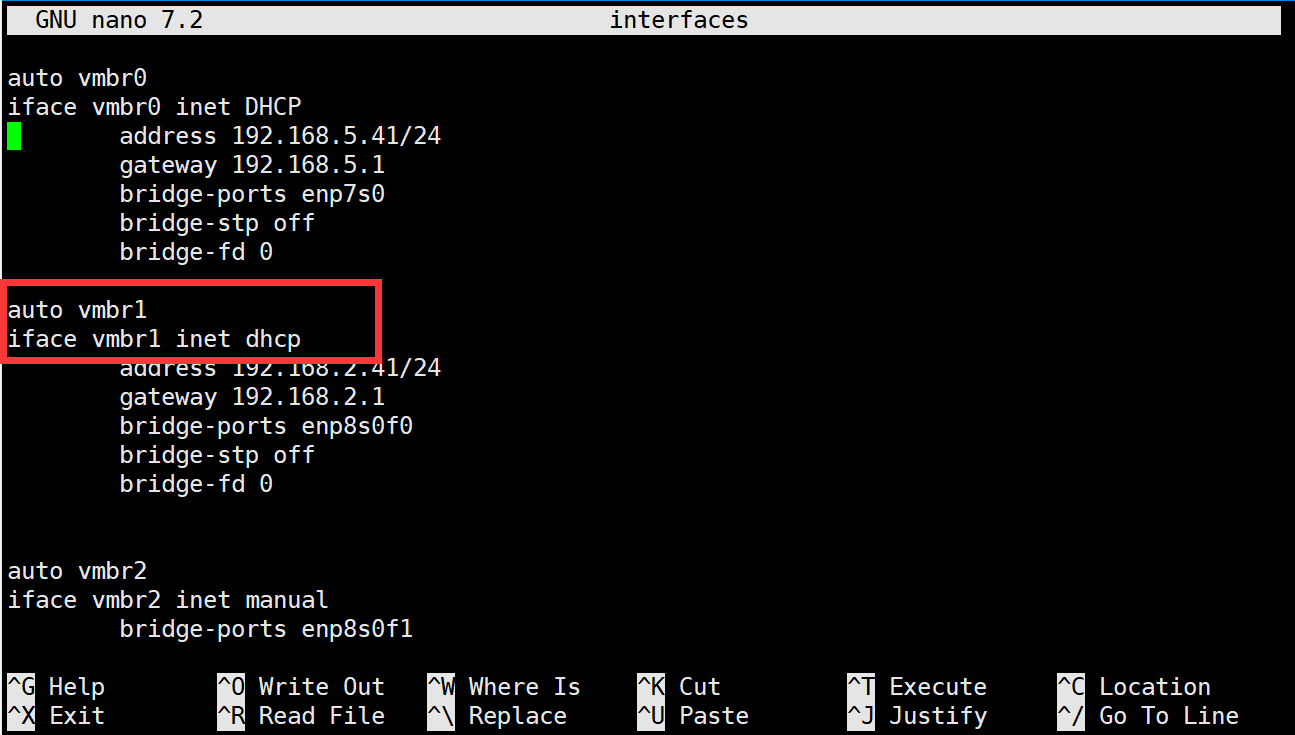
pve安装ikuai并设置,同时把pve的网络连接到ikuai虚拟机
目录 前因 前置条件 安装ikuai 进入ikuai的后台 配置lan口,以及wan口 配置lan口桥接 按实际情况来设置了 单拨(PPOE拨号) 多拨(内外网设置点击基于物理网卡的混合模式) 后续步骤 pve连接虚拟机ikuai的网络以及其他虚拟机连接ikuai的网…...
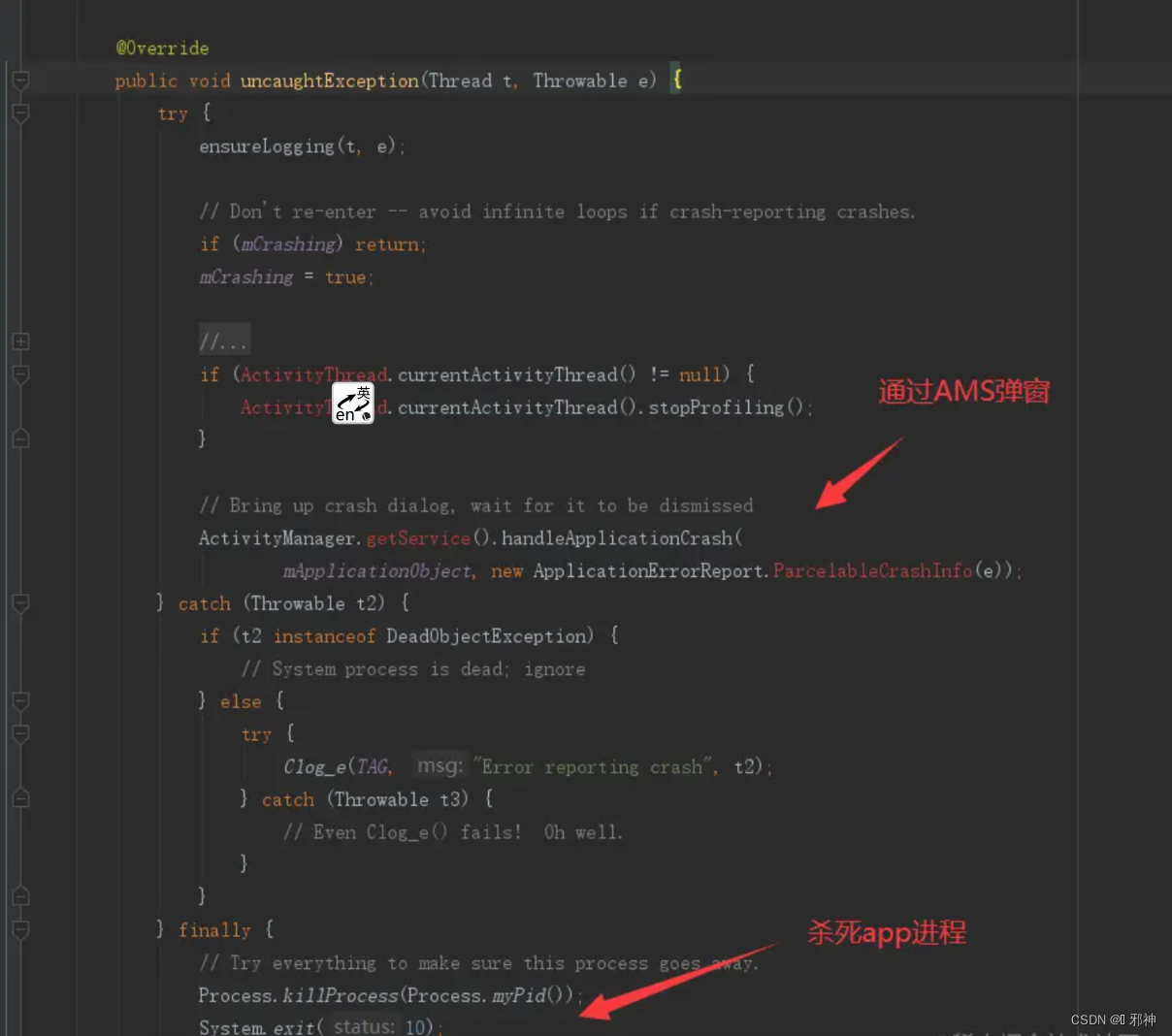
Android 面试题 ANR 五
🔥 什么是 ANR 🔥 ANR(Application Not Responding )应用无响应的简称,是为了在 APP卡死时,用户 可以强制退出APP的选择,从而避免卡机无响应问题,这是Android系统的一种自我保护机制。 在Android中…...

实训笔记7.28
实训笔记7.28 7.28笔记一、Hive的基本使用1.1 Hive的命令行客户端的使用1.2 Hive的JDBC客户端的使用1.2.1 使用前提1.2.2 启动hiveserver21.2.3 使用方式 1.3 Hive的客户端中也支持操作HDFS和Linux本地文件 二、Hive中DDL语法2.1 数据库的管理2.1.1 创建语法2.1.2 修改语法2.1.…...

C 游游的二进制树
题目描述 游游拿到了一棵树,共有nnn个节点,每个节点都有一个权值:0或者1。这样,每条路径就代表了一个二进制数。 游游想知道,有多少条路径代表的二进制数在[l,r][l,r][l,r]区间范围内? (请注意…...
收发存和进销存有什么区别?
一、什么是收发存和进销存 1、收发存 收发存是供应链管理中的关键概念,用于描述企业在供应链中的物流和库存管理过程。 收发存代表了企业在采购、生产和销售过程中的物流活动和库存水平。 收(Receiving) 企业接收供应商送达的物料或产品…...

小程序 账号的体验版正式版的账号信息及相关配置
siteinfo.js // 正式环境 const releaseConfig {appID: "",apiUrl: "",imgUrl: "" }; // 测试环境(包含开发环境和体验环境) const developConfig {appID: "",apiUrl: "",imgUrl: "" }…...
和 Web3对比,未来发展)
AIGC(Artificial Intelligence Generated Content)和 Web3对比,未来发展
一、AIGC(Artificial Intelligence Generated Content)行业 历史背景 AIGC(Artificial Intelligence Generated Content)是指利用人工智能技术生成的内容。随着人工智能技术的不断发展,AIGC 行业逐渐兴起。早期的 AIG…...
机器学习之Boosting和AdaBoost
1 Boosting和AdaBoost介绍 1.1 集成学习 集成学习 (Ensemble Learning) 算法的基本思想就是将多个分类器组合,从而实现一个预测效果更好的集成分类器。 集成学习通过建立几个模型来解决单一预测问题。它的工作原理是生成多个分类器/模型,各自独立地学…...

汇编语言预定义寄存器和协处理器
ARM汇编器对ARM的寄存器和协处理器进行了预定义(包括APCS对r0~r15寄存器的定义),所有的寄存器和协处理器名都是大小写敏感的。 (1)预定义寄存器名 下面列出了被ARM汇编器预定义的寄存器名。 r0ÿ…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...
