【EI/SCOPUS会议征稿】2023年第四届新能源与电气科技国际学术研讨会 (ISNEET 2023)

作为全球科技创新大趋势的引领者,中国一直在为科技创新创造越来越开放的环境,提高学术合作的深度和广度,构建惠及全民的创新共同体。这些努力为全球化和创建共享未来的共同体做出了新的贡献。
为交流近年来国内外在新能源和电气技术领域的最新进展,由浙江水利水电学院主办,2023年第四届新能源与电气科技国际学术研讨会 (ISNEET 2023)将于2023年10月20-22日在中国浙江湖州召开。ISNEET 2023 欢迎研究人员,工程师,科学家和行业专家参加一个开放式论坛,在此论坛上可以共享和讨论新能源和电气技术领域的进步。 该会议是跟上不断变化的领域的进步和变化的理想平台, 来自世界各地的领先研究人员和行业专家将通过论文和口头报告来介绍最新研究。
重要信息
大会官网:http://www.isneet.org (点击参会/投稿)
会议时间:2023年10月20-22日
会议地点:中国-浙江湖州
接受/拒稿通知:投稿后1周内
征稿主题
| 可再生能源系统 太阳能 生物质能 风能 波浪和潮汐能源 地热能 核能 生物能源 氢气和燃料电池 能源材料 | 电机和驱动 电力转换器 电瓶和BMS 储能技术 控制策略和算法 人工智能 设计和优化 智能电网 运输电气化 新能源汽车、电动汽车 | 节约能源技术 输电和配电 能源管理系统 制造、测试和标准 能源效率系统 可靠性和诊断 噪声、振动、EMI和EMC 电能质量 电力系统分析 经济分析 社会和环境的可持续性 |
* 以上相关主题亦可投稿,更多征稿主题见官网
论文出版
A. EI会议论文
所有的投稿论文都必须经过2-3位组委会专家审稿,经过严格的审稿之后,最终所有录用的论文将以会议论文集的形式发表,见刊后提交EI Compendex和Scopus检索收录。
◆会议论文模板下载见官网。
◆会议仅接受全英稿件。
投稿须知:
① 论文应具有学术或实用价值,且未在国内外学术期刊或会议发表过;
② 作者可通过CrossCheck, Turnitin或其他查询系统自费查重;
③ 因作者原因申请的撤稿,需扣手续费(具体退费政策详情见官网);
④论文不得少于5页;
2. SCI期刊
优秀的论文可推荐至SCI期刊发表
*Sustainable Energy Technologies and Assessments
ISSN: 2213-1388,IF: 5.353
Indexing:SCIE
* Energies
ISSN: 1996-1073, IF: 3.252
Indexing:SCIE
参会须知
1、作者参会:一篇录用文章需安排一名作者参会;
2、主旨报告:可申请主题演讲,由组委会审核;
3、口头报告:可申请口头报告,时间为15分钟;
4、海报展示:可申请海报展示,A1尺寸,彩色打印;
5、听众参会:不投稿仅参会,也可申请演讲及展示;
相关文章:

【EI/SCOPUS会议征稿】2023年第四届新能源与电气科技国际学术研讨会 (ISNEET 2023)
作为全球科技创新大趋势的引领者,中国一直在为科技创新创造越来越开放的环境,提高学术合作的深度和广度,构建惠及全民的创新共同体。这些努力为全球化和创建共享未来的共同体做出了新的贡献。 为交流近年来国内外在新能源和电气技术领域的最新…...
【计算机网络】10、ethtool
文章目录 一、ethtool1.1 常见操作1.1.1 展示设备属性1.1.2 改变网卡属性1.1.2.1 Auto-negotiation1.1.2.2 Speed 1.1.3 展示网卡驱动设置1.1.4 只展示 Auto-negotiation, RX and TX1.1.5 展示统计1.1.7 排除网络故障1.1.8 通过网口的 LED 区分网卡1.1.9 持久化配置(…...

什么是前端工程化?
工程化介绍 什么是前端工程化? 前端工程化是一种思想,而不是某种技术。主要目的是为了提高效率和降低成本,也就是说在开发的过程中可以提高开发效率,减少不必要的重复性工作等。 tip 现实生活举例 建房子谁不会呢?请…...

【深度学习】【三维重建】windows11环境配置tiny-cuda-nn详细教程
【深度学习】【三维重建】windows11环境配置tiny-cuda-nn详细教程 文章目录 【深度学习】【三维重建】windows11环境配置tiny-cuda-nn详细教程前言确定版本对应关系源码编译安装tiny-cuda-nn总结 前言 本人windows11下使用【Instant Neural Surface Reconstruction】算法时需要…...

Matlab 一种自适应搜索半径的特征提取方法
文章目录 一、简介二、实现代码参考资料一、简介 在之前的博客(C++ ID3决策树)中,提到过一种信息熵的概念,其中它表达的大致意思为:香农认为熵是指“当一件事情有多种可能情况时,这件事情发生某种情况的不确定性”,也就是指如果一个事情的不确定性越大,那么这个信息的熵…...
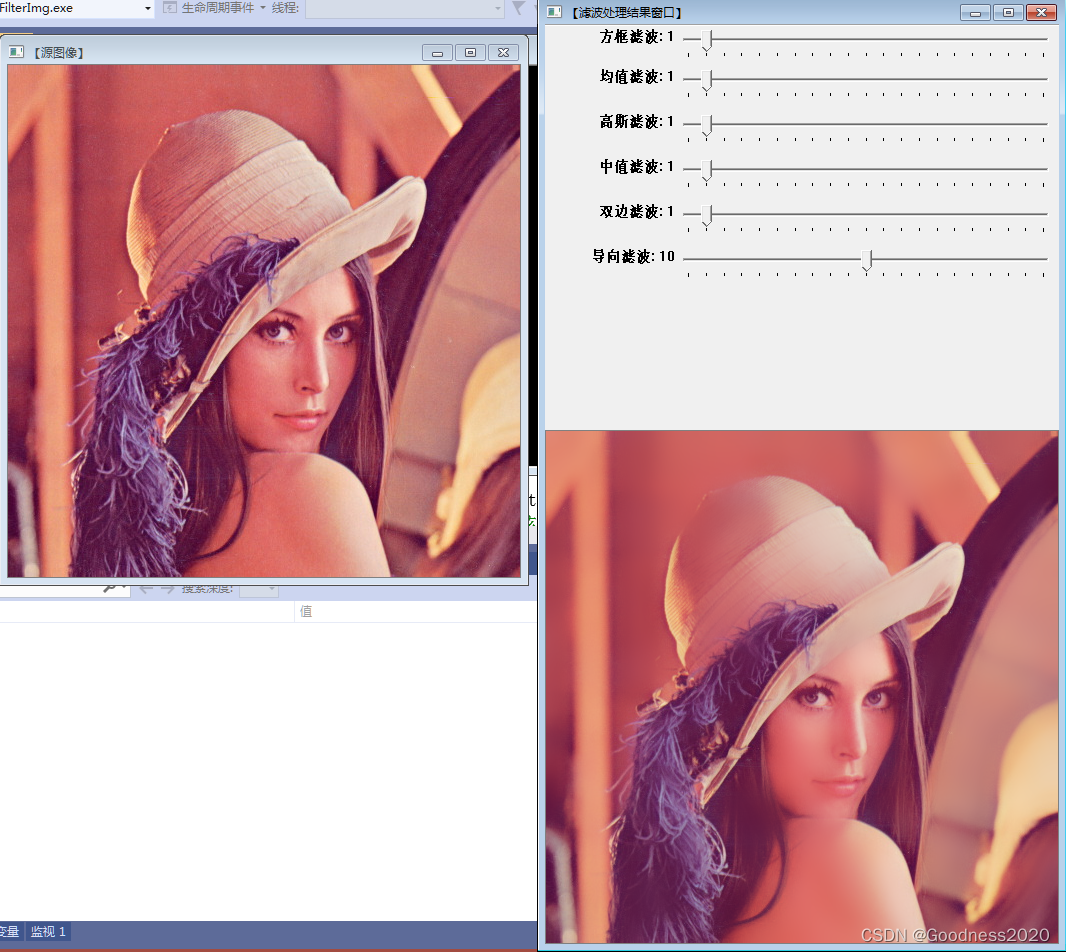
基于opencv的几种图像滤波
一、介绍 盒式滤波、均值滤波、高斯滤波、中值滤波、双边滤波、导向滤波。 boxFilter() blur() GaussianBlur() medianBlur() bilateralFilter() 二、代码 #include <opencv2/core/core.hpp> #include <opencv2/highgui/highgui.hpp> …...
puppeteer代理的搭建和配置
puppeteer代理的搭建和配置 本文深入探讨了Puppeteer在网络爬虫和自动化测试中的重要角色,着重介绍了如何搭建和配置代理服务器,以优化Puppeteer的功能和性能。文章首先介绍了Puppeteer作为一个强大的Headless浏览器自动化工具的优势和应用场景…...
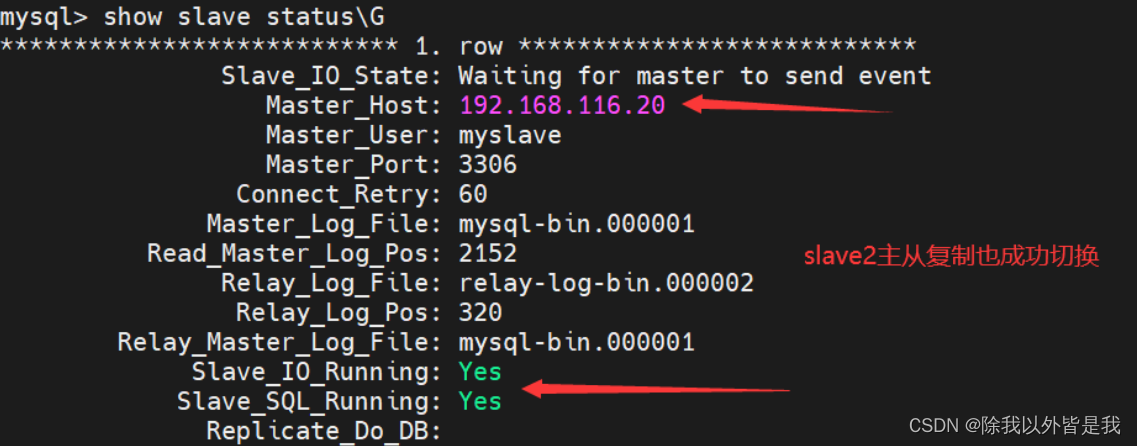
【简单认识MySQL的MHA高可用配置】
文章目录 一、简介1、概述2、MHA 的组成3.MHA 的特点4、MHA工作原理 二、搭建MHA高可用数据库群集1.主从复制2.MHA配置 三、故障模拟四、故障修复步骤: 一、简介 1、概述 MHA(Master High Availability)是一套优秀的MySQL高可用…...
【云原生】一文学会Docker存储所有特性
目录 1.Volumes 1.Volumes使用场景 2.持久将资源存放 3. 只读挂载 2.Bind mount Bind mounts使用场景 3.tmpfs mounts使用场景 4.Bind mounts和Volumes行为上的差异 5.docker file将存储内置到镜像中 6.volumes管理 1.查看存储卷 2.删除存储卷 3.查看存储卷的详细信息…...

Android Ble蓝牙App(一)扫描
Ble蓝牙App(一)扫描 前言正文一、基本配置二、扫描准备三、扫描页面① 增加UI布局② 点击监听③ 扫描处理④ 广播处理 四、权限处理五、扫描结果① 列表适配器② 扫描结果处理③ 接收结果 六、源码 前言 关于低功耗的蓝牙介绍我已经做过很多了࿰…...
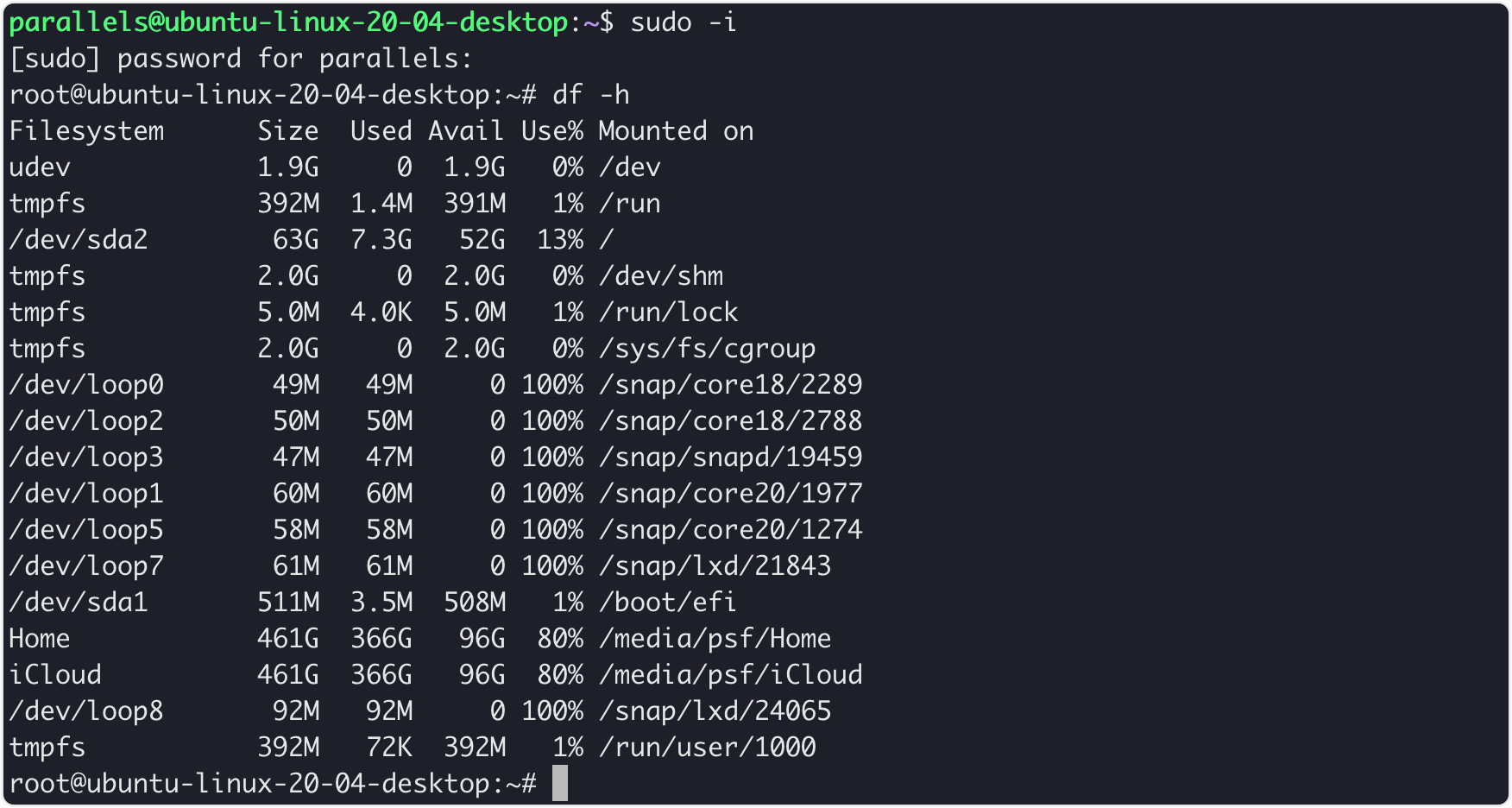
mac pd安装ubuntu并配置远程连接
背景 一个安静的下午,我又想去折腾点什么了。准备学习一下k8s的,但是没有服务器。把我给折腾的,在抱怨了:为什么M系列芯片的资源怎么这么少。 好在伙伴说,你可以尝试一下ubantu。于是,我只好在我的mac上安…...
1.3 eureka+ribbon,完成服务注册与调用,负载均衡源码追踪
本篇继先前发布的1.2 eureka注册中心,完成服务注册的内容。 目录 环境搭建 采用eurekaribbon的方式,对多个user服务发送请求,并实现负载均衡 负载均衡原理 负载均衡源码追踪 负载均衡策略 如何选择负载均衡策略? 饥饿加载…...

mysql修改字段长度是否锁表
Varchar对于小于等于255字节以内的长度可以使用一个byte 存储。大于255个字节的长度则需要使用2个byte存储 1, 如果是255长度之内的扩展,或者255之外的扩展,则不锁表,采用in-place方式执行 2, 如果从varchar长度从(0,2…...
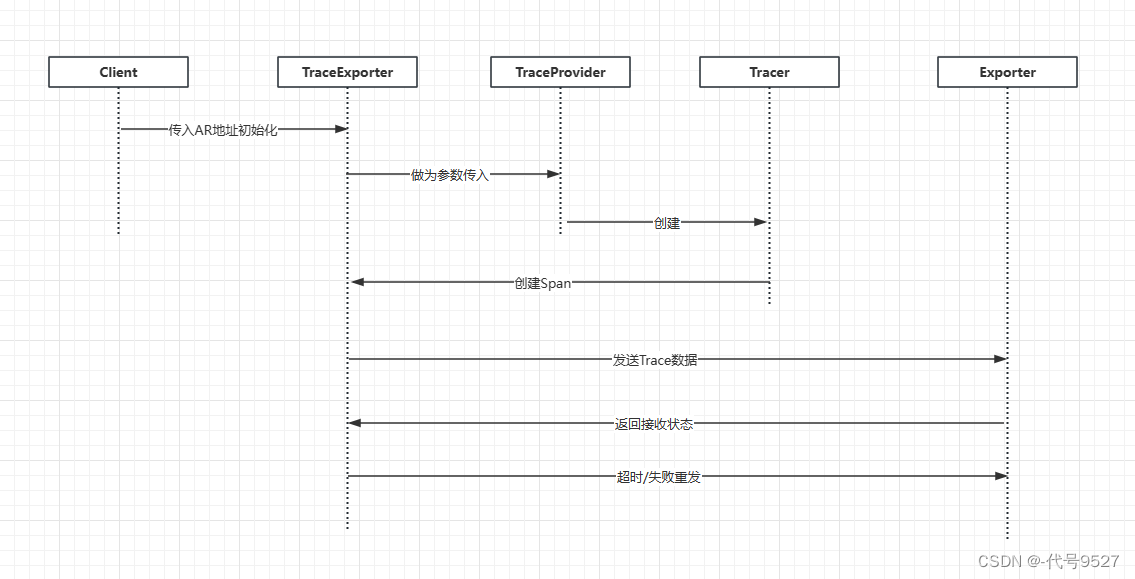
SpringCloud集成OpenTelemetry的实现
SpringCloud项目做链路追踪,比较常见的会集成SleuthZipKin来完成,但这次的需求要集成开源框架OpenTelemetry,这里整理下实现过程。相关文章: 【SpringCloud集成SleuthZipkin进行链路追踪】 【OpenTelemetry框架Trace部分整理】 …...
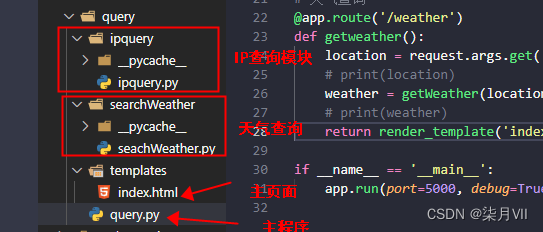
Python爬取IP归属地信息及各个地区天气信息
一、实现样式 二、核心点 1、语言:Python、HTML,CSS 2、python web框架 Flask 3、三方库:requests、xpath 4、爬取网站:https://ip138.com/ 5、文档结构 三、代码 ipquery.py import requests from lxml import etree # 请求…...
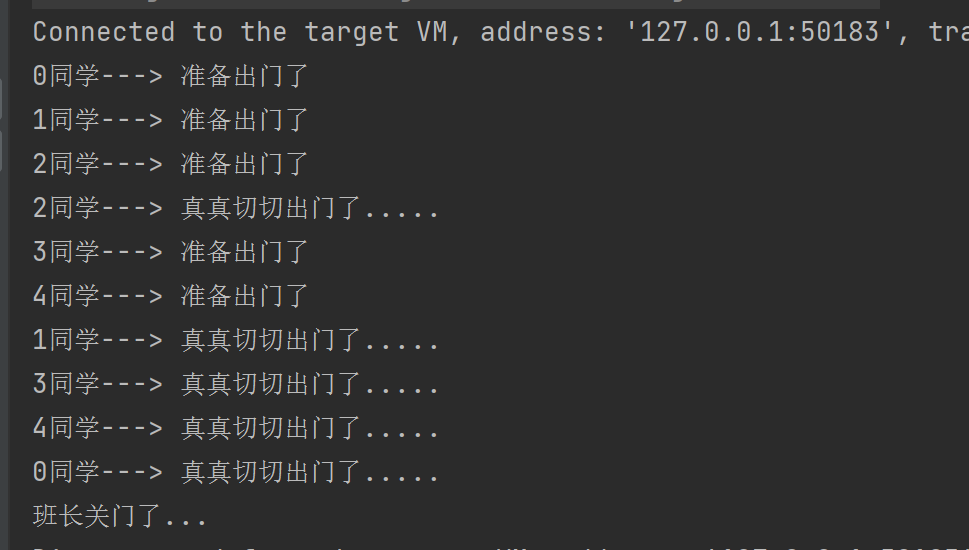
RedLock + Redisson
目录 2.9 RedLock2.9.1 上述实现的分布式锁在集群状态下失效的原因2.9.2 解决方式-RedLock 2.10 redisson中的分布式锁2.10.0 redisson简介以及简单使用简单使用redisson中的锁Redisson常用配置 2.10.1 Redisson可重入锁实现原理2.10.2 公平锁(Fair Lock)…...
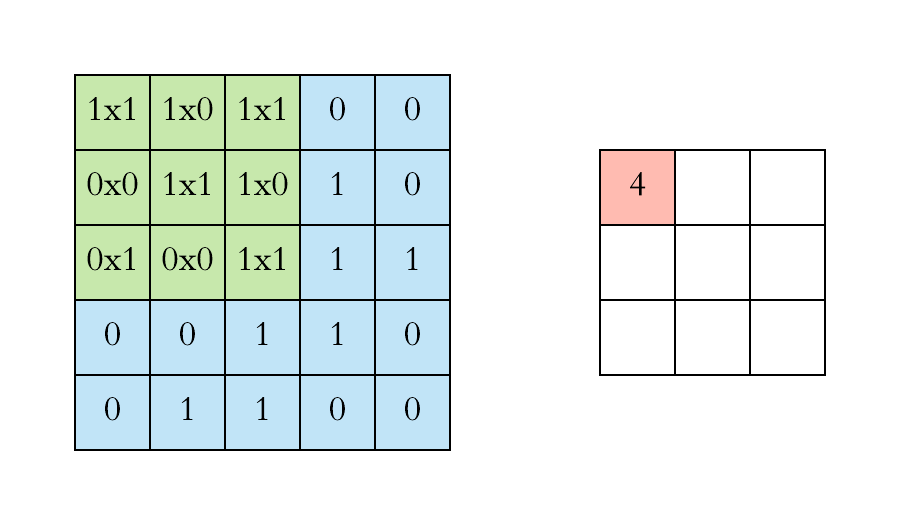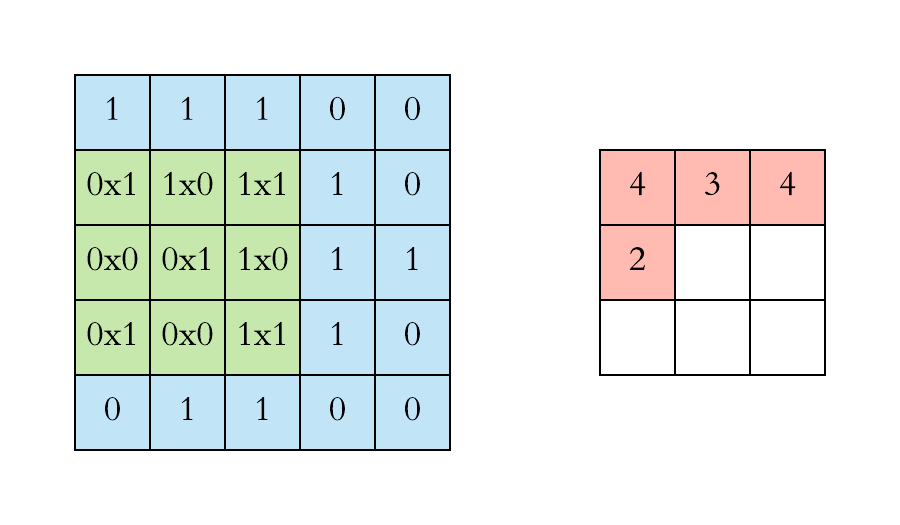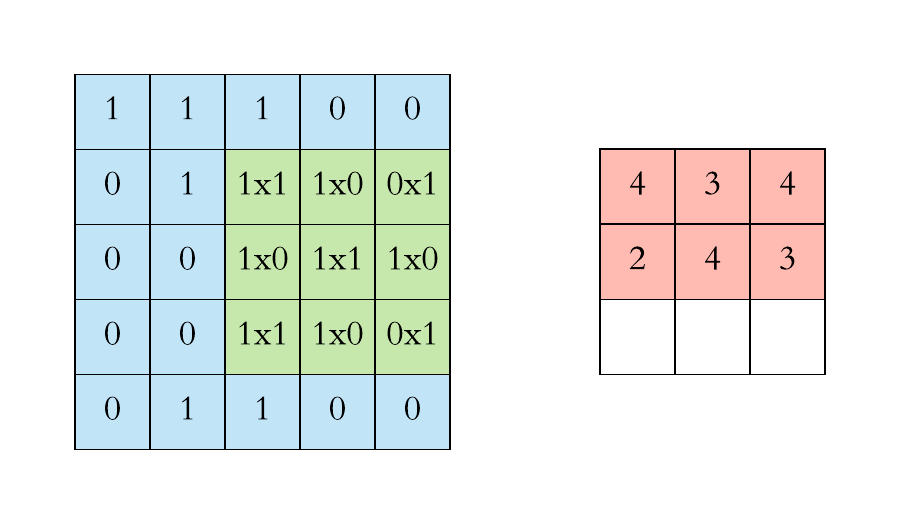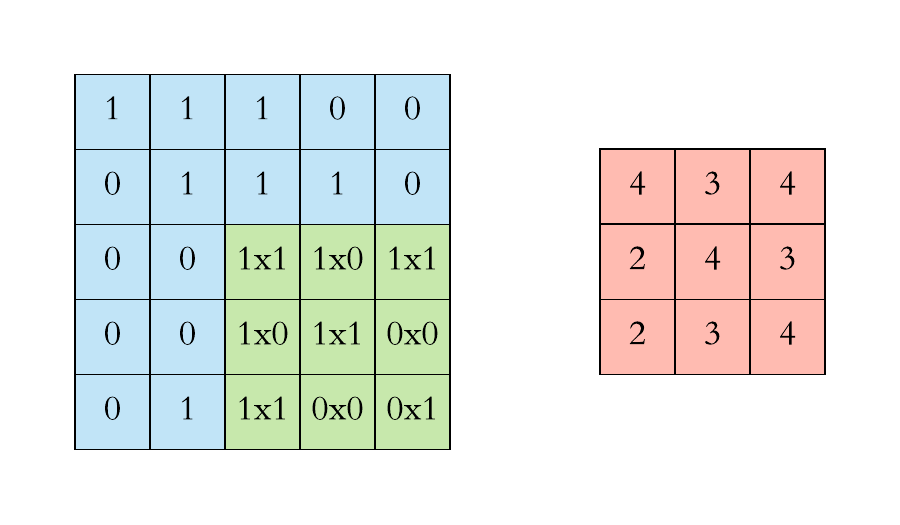
计算机视觉:卷积层的参数量是多少?
本文重点 卷积核的参数量是卷积神经网络中一个重要的概念,它决定了网络的复杂度和计算量。在深度学习中,卷积操作是一种常用的操作,用于提取图像、语音等数据中的特征。卷积神经网络的优势点在于稀疏连接和权值共享,这使得卷积核的参数相较于传统的神经网络要少很多。 举例…...
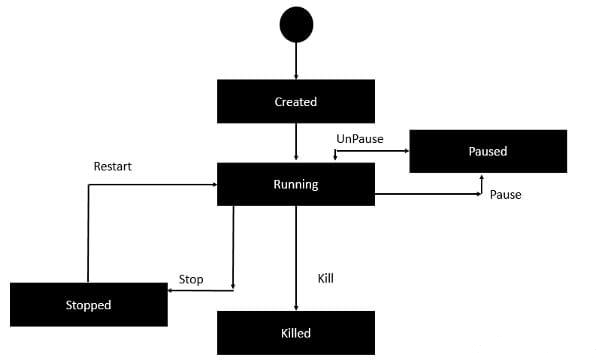
Docker 容器基础操作
Docker容器基础操作 容器(container)是Docker镜像的运行实例,类似于可执行文件与进程的关系,Docker是容器引擎,相当于系统平台。 容器的生命周期 容器的基础操作(以 tomcat8.0 为例) # 拉取tomcat8.0镜像 [root@tudou tudou]# docker pull tomcat:8.0 8.0: Pulling f…...
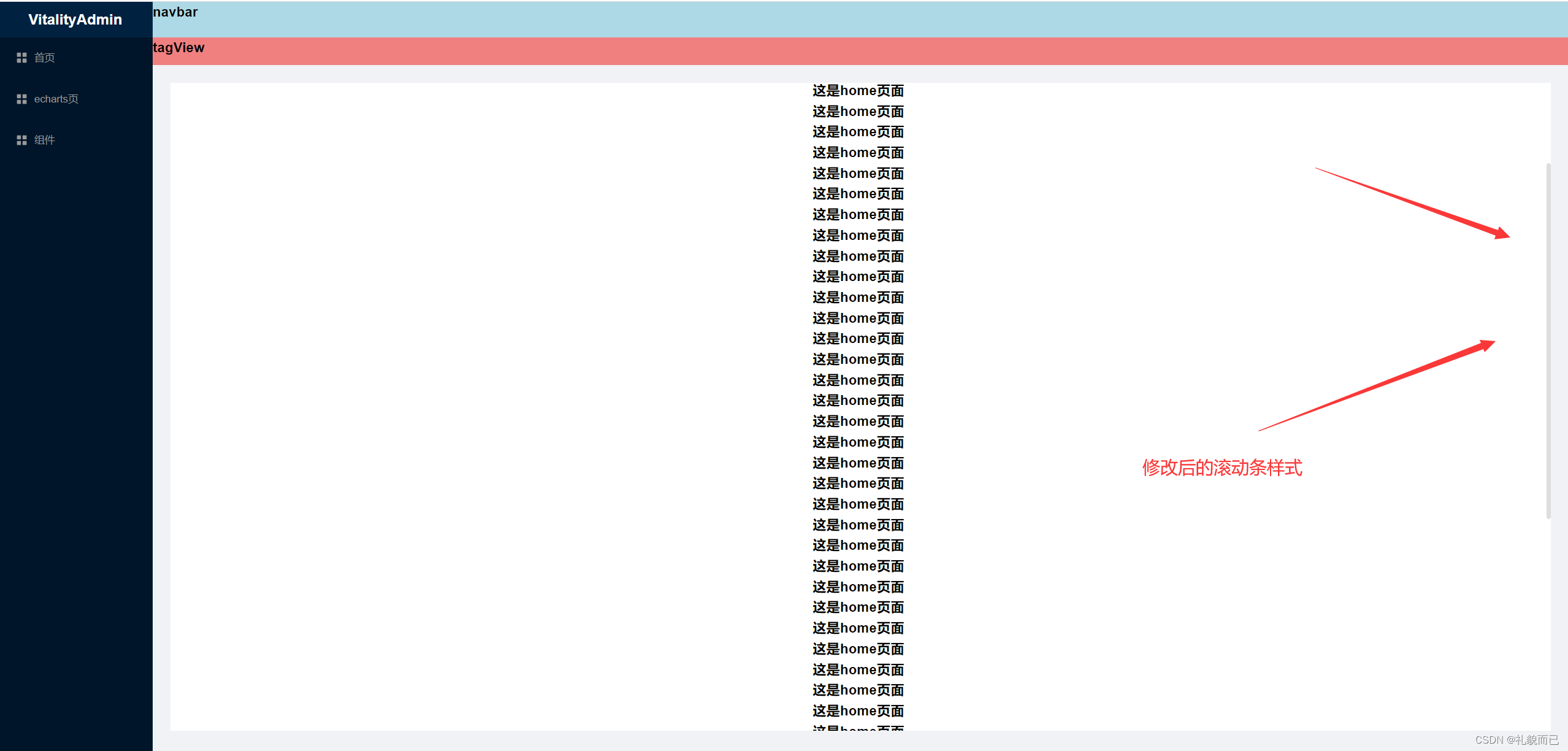
【Vue3+Ts+Vite】配置滚动条样式
一、先看效果 二、直接上代码 <template><div class"main-container"><h1 v-for"index in 50" :key"index">这是home页面</h1></div> </template> <style lang"scss" scoped> .main-conta…...

react map使用方法详解
在React中,map()方法是用于数组的常见方法之一,它可以用于处理数组并返回一个新的数组。在React中,经常使用map()方法来遍历数组,生成对应的组件列表或进行数据转换操作。 下面是map()方法在React中的使用方法详解: …...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...
