leetcode1219. 黄金矿工(java)
黄金矿工
- leetcode1219. 黄金矿工
- 题目描述
- 回溯算法
- 代码
- 回溯算法
leetcode1219. 黄金矿工
难度: 中等
eetcode 1219 黄金矿工
题目描述
你要开发一座金矿,地质勘测学家已经探明了这座金矿中的资源分布,并用大小为 m * n 的网格 grid 进行了标注。每个单元格中的整数就表示这一单元格中的黄金数量;如果该单元格是空的,那么就是 0。
为了使收益最大化,矿工需要按以下规则来开采黄金:
每当矿工进入一个单元,就会收集该单元格中的所有黄金。
矿工每次可以从当前位置向上下左右四个方向走。
每个单元格只能被开采(进入)一次。
不得开采(进入)黄金数目为 0 的单元格。
矿工可以从网格中 任意一个 有黄金的单元格出发或者是停止。
示例 1:
输入:grid = [[0,6,0],[5,8,7],[0,9,0]]
输出:24
解释:
[[0,6,0],
[5,8,7],
[0,9,0]]
一种收集最多黄金的路线是:9 -> 8 -> 7。
示例 2:
输入:grid = [[1,0,7],[2,0,6],[3,4,5],[0,3,0],[9,0,20]]
输出:28
解释:
[[1,0,7],
[2,0,6],
[3,4,5],
[0,3,0],
[9,0,20]]
一种收集最多黄金的路线是:1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7。
提示:
1 <= grid.length, grid[i].length <= 15
0 <= grid[i][j] <= 100
最多 25 个单元格中有黄金。
回溯算法
首先了解什么是回溯算法:
解决一个回溯问题,实际上就是一个决策树的遍历过程,站在回溯树的一个节点上,你只需要思考 3 个问题:
- 路径:也就是已经做出的选择。
- 选择列表:也就是你当前可以做的选择。
- 结束条件:也就是到达决策树底层,无法再做选择的条件。
代码框架:
result = []
def backtrack(路径, 选择列表):if 满足结束条件:result.add(路径)returnfor 选择 in 选择列表:做选择backtrack(路径, 选择列表)撤销选择关于本体的解题思路:
我们首先在 m×nm \times nm×n 个网格内枚举起点。只要格子内的数大于 000,它就可以作为起点进行开采。
记枚举的起点为 (i,j),我们就可以从 (i,j)开始进行递归 + 回溯,枚举所有可行的开采路径。我们用递归函数 dfs(x,y,gold)\进行枚举,其中 (x,y)(x, y)(x,y) 表示当前所在的位置,gold\textit{gold}gold 表示在开采位置 (x,y)(x, y)(x,y) 之前,已经拥有的黄金数量。根据题目的要求,我们需要进行如下的步骤:
我们需要将 gold 更新为 gold+grid[x][y],表示对位置(x,y) 进行开采。由于我们的目标是最大化收益,因此我们还要维护一个最大的收益值 ans,并在这一步使用 gold\textit{gold}gold 更新ans;
我们需要枚举矿工下一步的方向。由于矿工每次可以从当前位置向上下左右四个方向走,因此我们需要依次枚举每一个方向。如果往某一个方向不会走出网格,并且走到的位置的值不为 0,我们就可以进行递归搜索;
在搜索完所有方向后,我们进行回溯。
代码
class Solution {int[][]g;int m,n;//标记已经走过的路线boolean[][]vis;//标记四个方向,矿工每到一个地方,都有四个方向可以选择.int[][]dirs = new int[][]{{1,0},{-1,0},{0,-1},{0,1}};public int getMaximumGold(int[][]gird){g = gird;m = g.length;n = g[0].length;vis = new boolean[m][n];int ans = 0;for (int i = 0; i < m;i++){for (int j = 0; j < n;j++){if (g[i][j] != 0){vis[i][j] = true;ans = Math.max(ans,dfs(i,j));vis[i][j] = false;}}}return ans;}/*** 开始回溯计算,每个点向四个方向开始移动的最大值* @param i* @param j* @return*/public int dfs(int i,int j){int ans = g[i][j];//枚举四个方向for (int[]d : dirs){int ni = i + d[0];int nj = j + d[1];if (ni < 0 || nj < 0 || ni >= m || nj >= n){continue;}if (g[ni][nj] == 0){continue;}//已经走过的不在重复计算if (vis[ni][nj]){continue;}//标记已选vis[ni][nj] = true;ans = Math.max(ans,g[i][j] + dfs(ni,nj));vis[ni][nj] = false;}return ans;}
}
回溯算法
leetcode698. 划分为k个相等的子集
leetcode93. 复原 IP 地址
leetcode306. 累加数
相关文章:
)
leetcode1219. 黄金矿工(java)
黄金矿工 leetcode1219. 黄金矿工题目描述回溯算法代码 回溯算法 leetcode1219. 黄金矿工 难度: 中等 eetcode 1219 黄金矿工 题目描述 你要开发一座金矿,地质勘测学家已经探明了这座金矿中的资源分布,并用大小为 m * n 的网格 grid 进行了标注。每个单元…...

Svelte框架入门
关键词 前端框架、编译器、响应式、模板 介绍 Svelte /svelt/ adj. 苗条的;线条清晰的;和蔼的 Svelte是一个前端组件框架,就像它的英文名字一样,Svelte的目标是打造一个更高性能的响应性前端框架。 Svelte类似于React和Vue框架&am…...
在linux中进行arm交叉编译体验tiny6410裸机程序开发流程
在某鱼上找了一个友善之臂的Tiny6410开发板用来体验一下嵌入式开发。这次先体验一下裸机程序的开发流程,由于这个开发板比较老旧了,官方文档有很多过期的内容,所以记录一下整个过程。 1. 交叉编译器安装 按照光盘A中的文档《04- Tiny6410 L…...
SpringBoot实战(二十三)集成 SkyWalking
目录 一、简介二、拉取镜像并部署1.拉取镜像2.运行skywalking-oap容器3.运行skywalking-ui容器4.访问页面 三、下载解压 agent1.下载2.解压 四、创建 skywalking-demo 项目1.Maven依赖2.application.yml3.DemoController.java 五、构建启动脚本1.startup.bat2.执行启动脚本3.发…...
深度学习实践——卷积神经网络实践:裂缝识别
深度学习实践——卷积神经网络实践:裂缝识别 系列实验 深度学习实践——卷积神经网络实践:裂缝识别 深度学习实践——循环神经网络实践 深度学习实践——模型部署优化实践 深度学习实践——模型推理优化练习 深度学习实践——卷积神经网络实践ÿ…...
linux | vscode | makefile | c++编译和调试
简单介绍环境: vscode 、centos、 gcc、g、makefile 简单来说就是,写好项目然后再自己写makefile脚本实现编译。所以看这篇博客的用户需要了解gcc编译的一些常用命令以及makefile语法。在网上看了很多教程,以及官网也看了很多次,最…...

Spring | Bean 作用域和生命周期
一、通过一个案例来看 Bean 作用域的问题 Spring 是用来读取和存储 Bean,因此在 Spring 中 Bean 是最核心的操作资源,所以接下来我们深入学习⼀下 Bean 对象 假设现在有⼀个公共的 Bean,提供给 A 用户和 B 用户使用,然而在使用的…...
)
培训(c++题解)
题目描述 某培训机构的学员有如下信息: 姓名(字符串)年龄(周岁,整数)去年 NOIP 成绩(整数,且保证是 5 的倍数) 经过为期一年的培训,所有同学的成绩都有所提…...
ansible-playbook编写 lnmp 剧本
ansible-playbook编写 lnmp 剧本 vim /opt/lnmp/lnmp.yaml执行剧本 ansible-playbook lnmp.yaml...

需求太多处理不过来?MoSCoW模型帮你
一、MoSCoW模型是什么 MoSCoW模型 是在项目管理、软件开发中使用的一种排序优先级的方法,以便开发人员、产品经理、客户对每个需求交付的重要性达成共识。 MoSCoW是一个首字母缩略词,代表: M(Must have):…...
Vue 3:玩一下web前端技术(六)
前言 本章内容为VUE请求后端技术与相关技术讨论。 上一篇文章地址: Vue 3:玩一下web前端技术(五)_Lion King的博客-CSDN博客 下一篇文章地址: Vue 3:玩一下web前端技术(七)_Lio…...

【点云处理教程】00计算机视觉的Open3D简介
一、说明 Open3D 是一个开源库,使开发人员能够处理 3D 数据。它提供了一组用于 3D 数据处理、可视化和机器学习任务的工具。该库支持各种数据格式,例如 .ply、.obj、.stl 和 .xyz,并允许用户创建自定义数据结构并在程序中访问它们。 Open3D 广…...
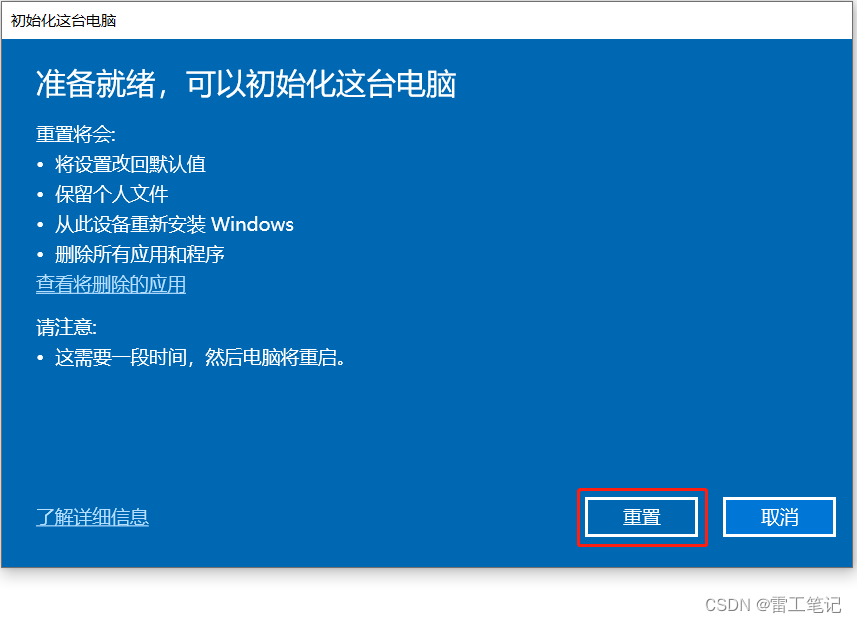
Windows10系统还原操作
哈喽,大家好,我是雷工! 复制了下虚拟机的Win10系统,但其中有一些软件,想实现类似手机的格式化出厂操作,下面记录Windows10系统的还原操作。 一、系统环境: 虚拟机内的Windows10,64…...
基础)
Django学习笔记-模板(Template)基础
使用模块可以很方便的执行一些数据操作,然后根据传入的数据直接在模板html文件中进行处理。 1.Django中的模板配置 Django的模板引擎在sttings.py文件中: TEMPLATES [{# 模板引擎,默认为django模板BACKEND: django.template.backends.dja…...

使用 NVM(Node Version Manager)管理 Node.js 版本
使用 NVM(Node Version Manager)管理 Node.js 版本 步骤一:安装 NVM NVM 是一个用于安装和管理不同版本的 Node.js 的工具。首先,你需要确保你的系统上已经安装了 NVM。可以通过以下命令检查 NVM 是否已经安装: nvm …...

(文章复现)梯级水光互补系统最大化可消纳电量期望短期优化调度模型matlab代码
参考文献: [1]罗彬,陈永灿,刘昭伟等.梯级水光互补系统最大化可消纳电量期望短期优化调度模型[J].电力系统自动化,2023,47(10):66-75. 1.基本原理 1.1 目标函数 考虑光伏出力的不确定性,以梯级水光互补系统的可消纳电量期望最大为目标,函数…...

tinkerCAD案例:24. Ruler - Measuring Lengths 标尺 -量勺
tinkerCAD案例:24. Ruler - Measuring Lengths 标尺 - 测量长度 Project Overview: 项目概况: A machine shop, where any idea can become a reality, can cost millions and million of dollars. Still, the most important tool in the shop is the…...

linux系统编程重点复习--线程同步
目录 复习目标: 1 互斥锁 1.1互斥锁的使用步骤 1.2 练习 1.3 死锁 2 读写锁 3 条件变量 4 信号量 复习目标: 熟练掌握互斥量的使用说出什么叫死锁以及解决方案熟练掌握读写锁的使用熟练掌握条件变量的使用理解条件变量实现的生产消费者模型理解…...
【Docker 学习笔记】Windows Docker Desktop 安装
文章目录 一、前言二、Windows Docker 安装1. 基于Hyper-V后端和Windows容器的安装2. 基于WSL2后端的安装(推荐)3. 安装Docker Desktop on Windows4. 启动并验证Docker Desktop 一、前言 Docker并非是一个通用的容器工具,它依赖于已存在并运…...

getInputStream has already been called for this request 问题记录
问题背景 HttpServletRequest.getReader() HttpServletRequest.getInputStream() 不能在过滤器中读取一次二进制流(字符流),又在另外一个Servlet中读取一次,即一个InputSteam(BufferedReader)对象在被读取完成后,将无…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...
