【字节三面】41. 缺失的第一个正数
41. 缺失的第一个正数
解题思路
- 在原数组上进行操作 如果数字是2 将其放在索引为1的位置上
- 数字x 放在索引为x - 1的位置上
- 对于长度为n的数组 其中没有出现的最小正整数只能在[1,n + 1]
- 引入如果1 - n 这些数都出现了 那么答案就是n + 1
- 如果都没有出现完全 那么答案就在[1,n]中没有出现最小正整数
class Solution {public int firstMissingPositive(int[] nums) {// 字节三面 // 在原数组上进行操作 如果数字是2 将其放在索引为1的位置上// 数字x 放在索引为x - 1的位置上// 对于长度为n的数组 其中没有出现的最小正整数只能在[1,n + 1] // 引入如果1 - n 这些数都出现了 那么答案就是n + 1 // 如果都没有出现完全 那么答案就在[1,n]中没有出现最小正整数for(int i = 0; i < nums.length; i++){// 一个萝卜一个坑while(nums[i] > 0 && nums[i] <= nums.length && nums[nums[i] - 1] != nums[i]){check(nums, i, nums[i] - 1);// 交换操作}} // 找到第一个不匹配的位置for(int i = 0; i < nums.length; i++){if(nums[i] != i + 1){return i + 1;}} return nums.length + 1;}public void check(int[] nums, int index1, int index2) {// 互换位置int temp = nums[index1];nums[index1] = nums[index2];nums[index2] = temp;}
}相关文章:

【字节三面】41. 缺失的第一个正数
41. 缺失的第一个正数 解题思路 在原数组上进行操作 如果数字是2 将其放在索引为1的位置上数字x 放在索引为x - 1的位置上对于长度为n的数组 其中没有出现的最小正整数只能在[1,n 1]引入如果1 - n 这些数都出现了 那么答案就是n 1如果都没有出现完全 那么答案就在[1,n]中没…...

Linux echo命令与反引号、重定向符号以及管道符
echo echo命令echo结合反引号echo结合重定向符echo结合管道符 echo命令 Linux中的echo命令用于在终端输出指定的文本内容或变量值。 基本语法如下: echo [选项] [字符串]常用选项包括: -e:启用特殊字符的解析,例如\n表示换行符…...

HTML基础知识点总结
目录 1.HTML简介 2.HTML基础结构 主要字符: 3.基础知识 (一)p标签 (二)hr标签 (三)尖角号 (四)版权号 (五)div和span div span (六)列表 (1&…...
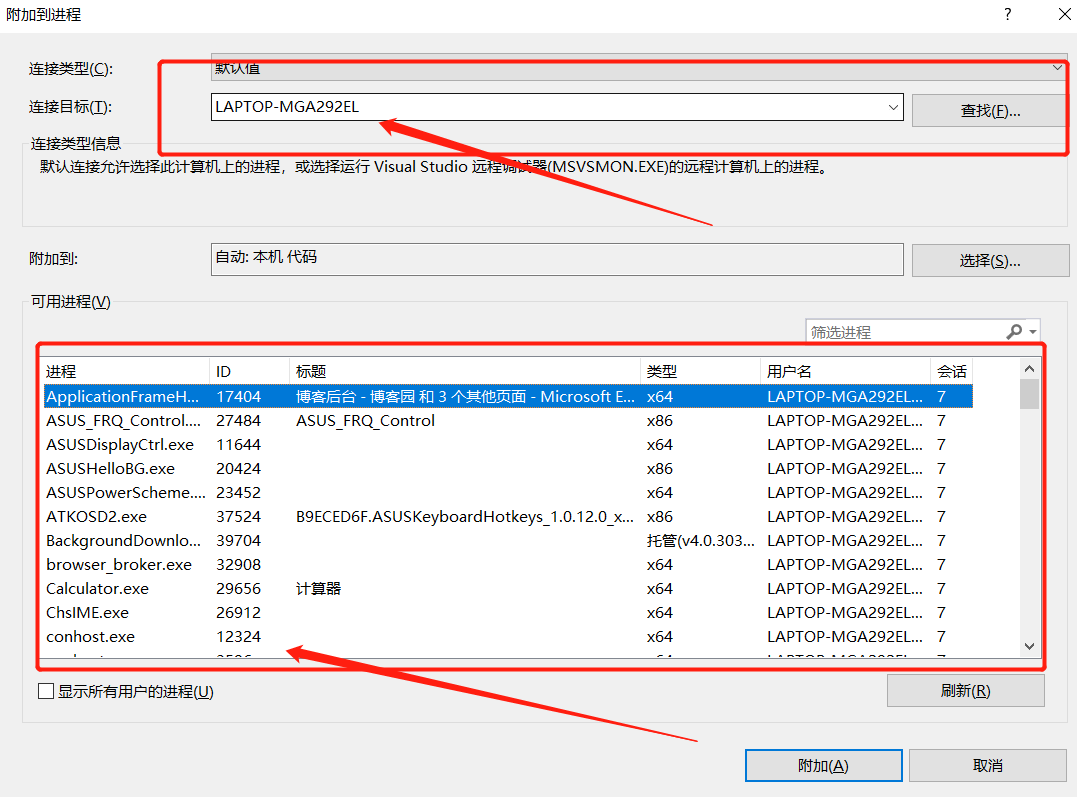
VS附加到进程调试
操作: 要附加到进程中调试外部可执行文件,您需要使用Visual Studio的“调试附加”功能。以下是附加到进程中调试外部可执行文件的步骤: 打开您要调试的源代码文件或可执行文件。打开Visual Studio。选择“调试”菜单,然后选择“…...
基于深度学习的高精度狗狗检测识别系统(PyTorch+Pyside6+YOLOv5模型)
摘要:基于深度学习的高精度狗狗检测识别系统可用于日常生活中检测与定位120类狗狗目标,利用深度学习算法可实现图片、视频、摄像头等方式的狗狗目标检测识别,另外支持结果可视化与图片或视频检测结果的导出。本系统采用YOLOv5目标检测模型训练…...
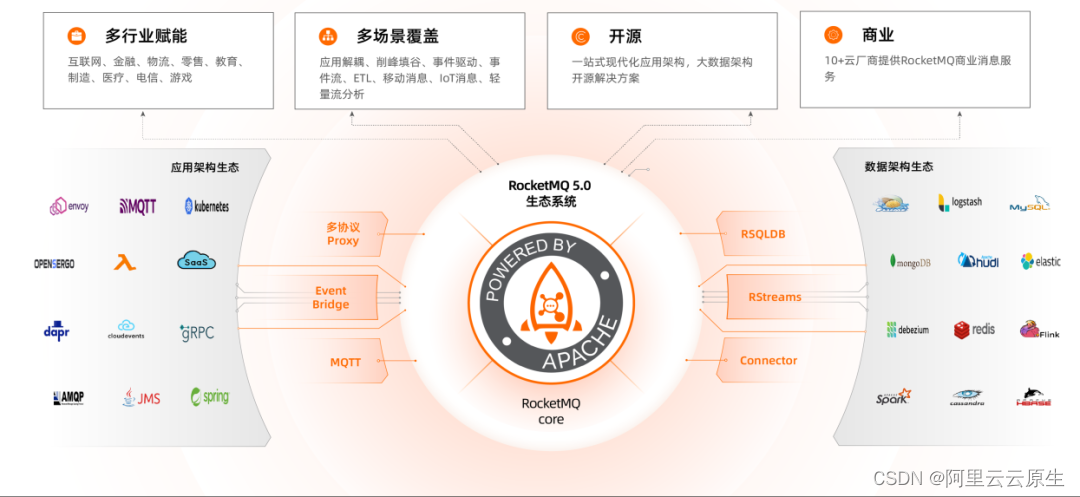
从互联网到云时代,Apache RocketMQ 是如何演进的?
作者:隆基 2022 年,RocketMQ 5.0 的正式版发布。相对于 4.0 版本而言,架构走向云原生化,并且覆盖了更多业务场景。 消息队列演进史 操作系统、数据库、中间件是基础软件的三驾马车,而消息队列属于最经典的中间件之一…...
)
XML (可扩展标记语言)
目录 一、概念 二. 使用: 1. 基本语法: 2. 组成部分: (1)文档声明 (2) 指令(了解):结合css (3) 标签:标签名称自定义 (4)…...
、bind()、listen()、htons())
socket()、bind()、listen()、htons()
socket() socket() 是一个系统调用函数,用于创建一个套接字(socket),通过该套接字进行网络通信。在这段代码中,socket() 函数被用于创建一个本地套接字。 具体来说,这是 socket() 在代码中的使用方式&…...
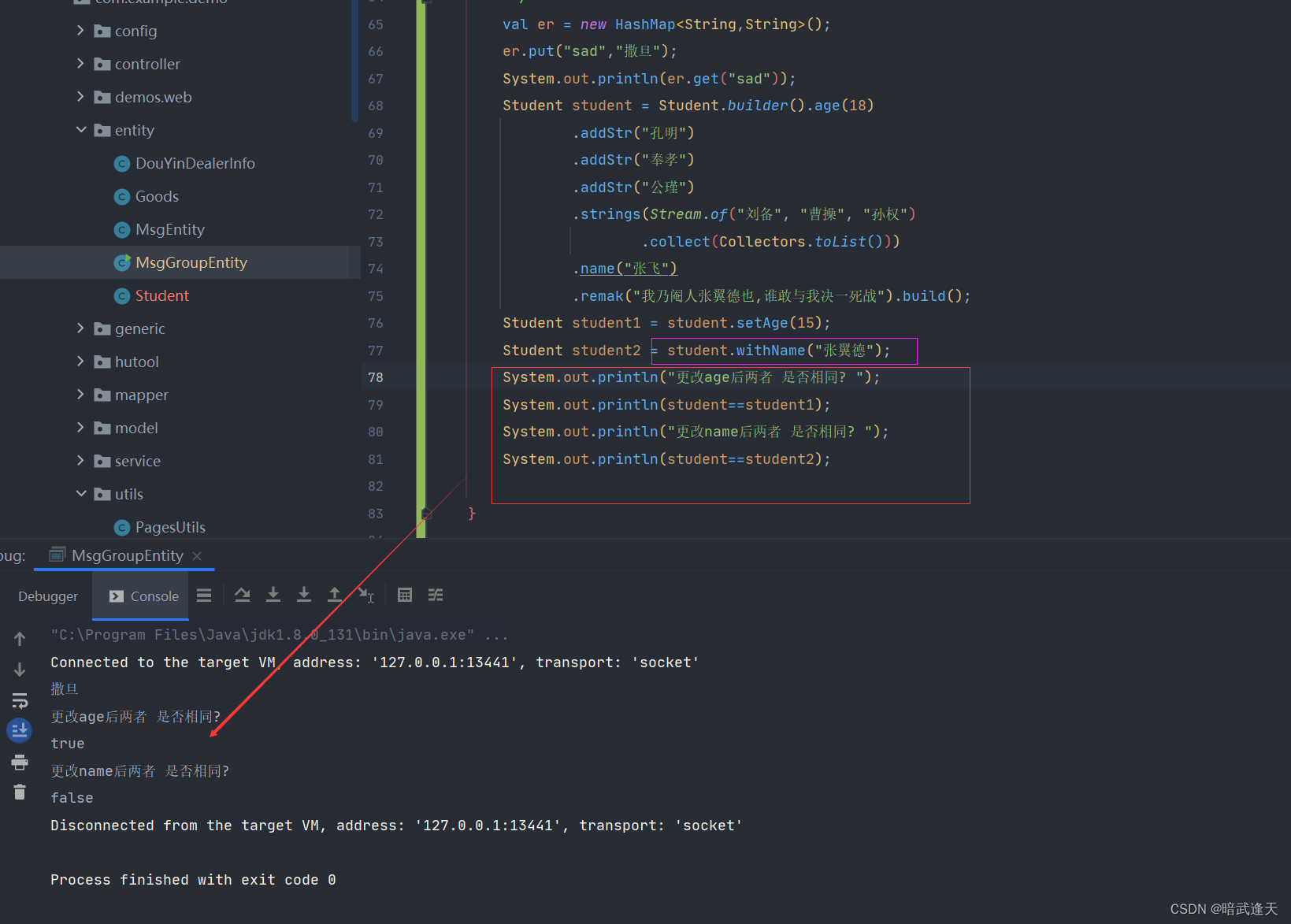
提升开发效率,Lombok的链式编程和构建模式
目录 链式编程 定义 代码示例 编辑 Accessors(chaintrue) 开启链式编程 编辑 Accessors(chain true,fluent true) 去除set和get 构建模式 定义 代码示例 编辑 踩坑 Singular 定义 代码示例 踩坑默认值情况 编辑 With 定义 代码示例 链式编程 定义 链…...

DuDuTalk:AI语音工牌如何帮助教培公司高效管理课程顾问团队
近年来,随着人工智能的快速发展,越来越多的公司开始利用AI技术来提高工作效率和管理效果。在教育培训行业中,课程顾问团队的管理对于公司的运营和发展至关重要。 而在实际管理中,受教培人员素质参差不齐,能力差异大&a…...

C语言——静态库和动态库的创建和使用
使用库函数是源码的一种保护 库函数其实不是新鲜的东西,我们一直都在用,比如C库。我们执行pringf() 这个函数的时候,就是调用C库的函数. 下面记录静态库和动态库的生成和使用. 静态库:libxxx.a 动态库:libxxx.so 静态库: 在程序编译的时候,将库编译进可执行程序中, 运行的…...
数学学习——最优化问题引入、凸集、凸函数、凸优化、梯度、Jacobi矩阵、Hessian矩阵
文章目录 最优化问题引入凸集凸函数凸优化梯度Jacobi矩阵Hessian矩阵 最优化问题引入 例如:有一根绳子,长度一定的情况下,需要如何围成一个面积最大的图像?这就是一个最优化的问题。就是我们高中数学中最常见的最值问题。 最优化…...
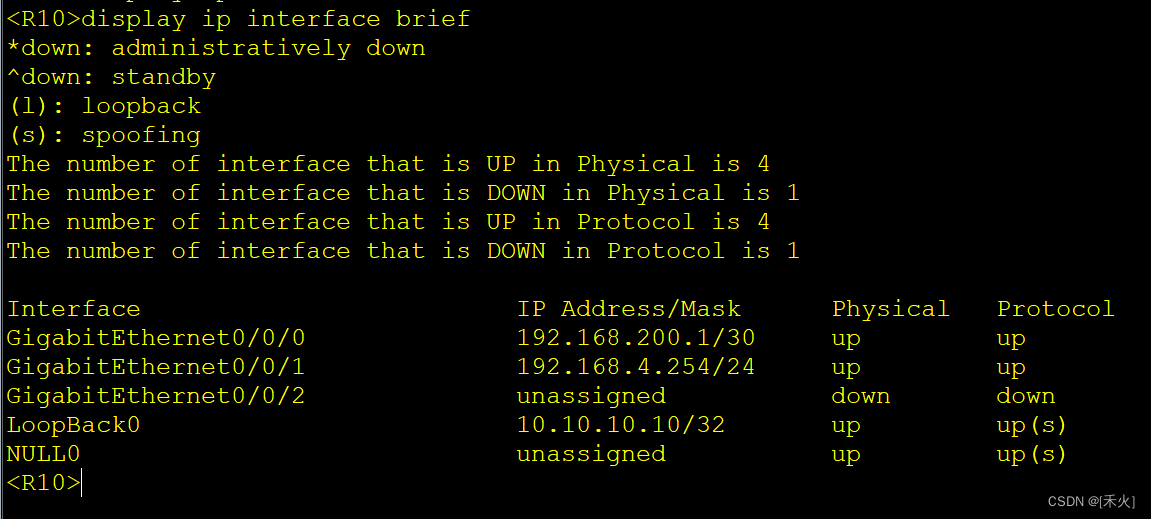
HCIP期中实验
考试需求 1 、该拓扑为公司网络,其中包括公司总部、公司分部以及公司骨干网,不包含运营商公网部分。 2 、设备名称均使用拓扑上名称改名,并且区分大小写。 3 、整张拓扑均使用私网地址进行配置。 4 、整张网络中,运行 OSPF 协议…...

【Git系列】IDEA集成Git
🐳IDEA集成Git 🧊1. idea配置git🧊2. idea添加暂存区和提交🪟创建文件🪟将整个项目添加到暂存区🪟提交到本地仓库🪟查看控制台,显示提交的信息🪟修改文件,再次…...
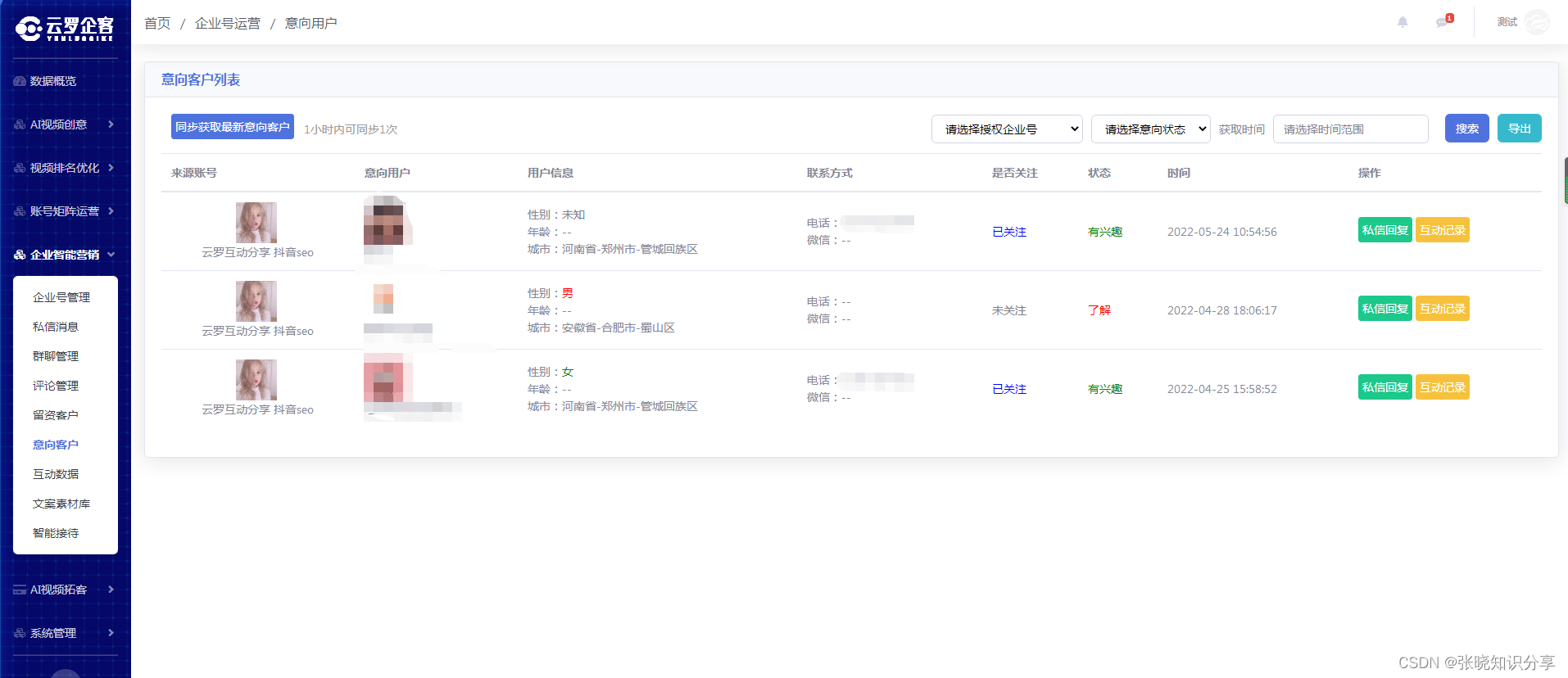
短视频矩阵源码开发搭建分享--多账号授权管理
目录 文章目录 前言 一、矩阵号系统是什么? 二、使用步骤 1.创建推广项目 2.多账号授权 3.企业号智能客服系统 总结 前言 短视频多账号矩阵系统,通过多账号一键授权管理的方式,为运营人员打造功能强大及全面的“矩阵式“管理平台。…...
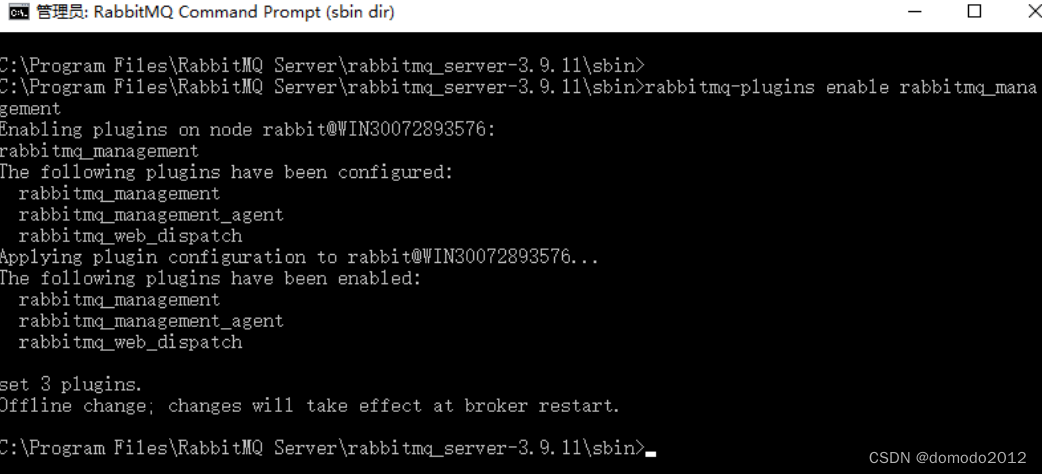
数据中台系列2:rabbitMQ 安装使用之 window 篇
RabbitMQ 是一个开源的消息队列系统,是高级消息队列协议(AMQP)的标准实现,用 erlang 语言开发。 因此安装 RabbitMQ 之前要先安装好 erlang。 1、安装 erlang 到 这里 下载本机能运行的最新版 erlang 安装包。如果本机没有装过 …...
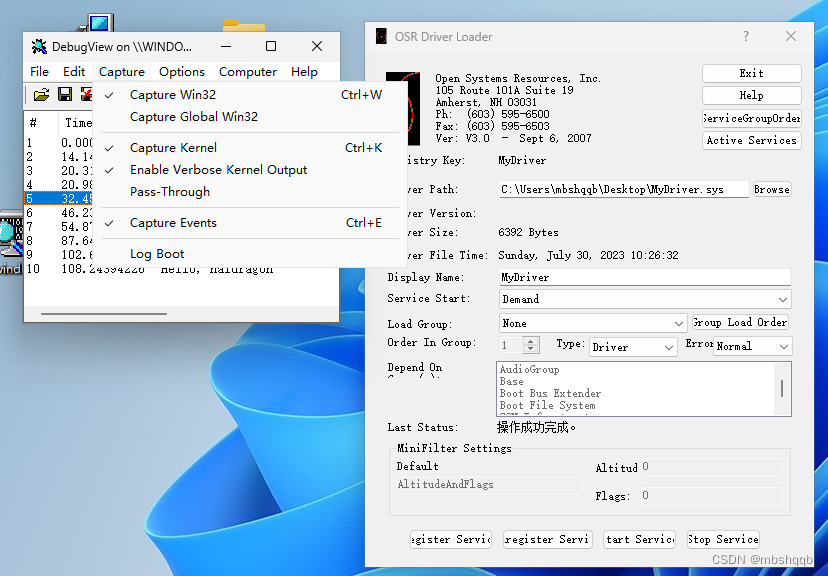
Windows驱动开发
开发Windows驱动程序时,debug比较困难,并且程序容易导致系统崩溃,这时可以使用Virtual Box进行程序调试,用WinDbg在主机上进行调试。 需要使用的工具: Virtual Box:用于安装虚拟机系统,用于运…...

汽车分析,随时间变化的燃油效率
简述 今天我们来分析一个汽车数据。 数据集由以下列组成: 名称:每辆汽车的唯一标识符。MPG:燃油效率,以英里/加仑为单位。气缸数:发动机中的气缸数。排量:发动机排量,表示其大小或容量。马力&…...

大数据面试题之Elasticsearch:每日三题(六)
大数据面试题之Elasticsearch:每日三题 1. 为什么要使用Elasticsearch?2.Elasticsearch的master选举流程?3.Elasticsearch集群脑裂问题? 1. 为什么要使用Elasticsearch? 系统中的数据,随着业务的发展,时间…...
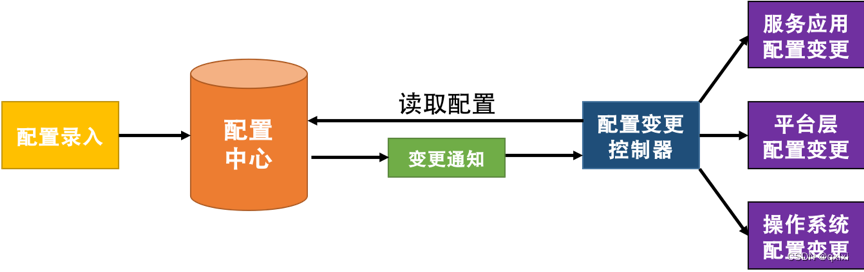
【管理设计篇】聊聊分布式配置中心
为什么需要配置中心 对于一个软件系统来说,除了数据、代码,还有就是软件配置,比如操作系统、数据库配置、服务配置 端口 ip 、邮箱配置、中间件软件配置、启动参数配置等。如果说是一个小型项目的话,可以使用Spring Boot yml文件…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...
