决策树的划分依据之:信息增益率
在上面的介绍中,我们有意忽略了"编号"这一列.若把"编号"也作为一个候选划分属性,则根据信息增益公式可计算出它的信息增益为 0.9182,远大于其他候选划分属性。
计算每个属性的信息熵过程中,我们发现,该属性的值为0, 也就是其信息增益为0.9182. 但是很明显这么分类,最后出现的结果不具有泛化效果.无法对新样本进行有效预测.
实际上,信息增益准则对可取值数目较多的属性有所偏好,为减少这种偏好可能带来的不利影响,著名的 C4.5 决策树算法 [Quinlan, 1993J 不直接使用信息增益,而是使用"增益率" (gain ratio) 来选择最优划分属性.
增益率:增益率是用前面的信息增益Gain(D, a)和属性a对应的"固有值"(intrinsic value) [Quinlan , 1993J的比值来共同定义的。
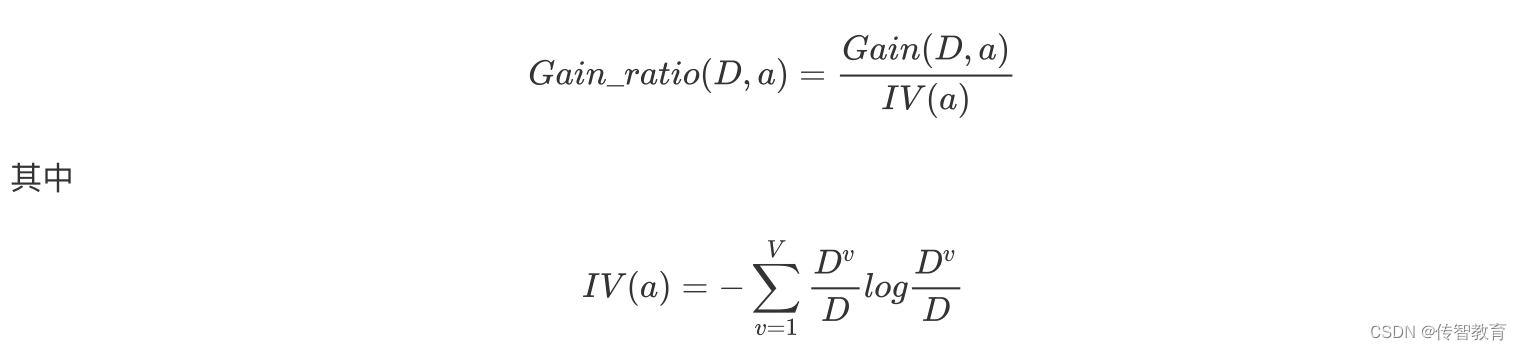
属性 a 的可能取值数目越多(即 V 越大),则 IV(a) 的值通常会越大.
案例一
a.计算类别信息熵
b.计算性别属性的信息熵(性别、活跃度)
c.计算活跃度的信息增益(性别、活跃度)
d.计算属性分裂信息度量
用分裂信息度量来考虑某种属性进行分裂时分支的数量信息和尺寸信息,我们把这些信息称为属性的内在信息(instrisic information)。信息增益率用信息增益/内在信息,会导致属性的重要性随着内在信息的增大而减小(也就是说,如果这个属性本身不确定性就很大,那我就越不倾向于选取它),这样算是对单纯用信息增益有所补偿。
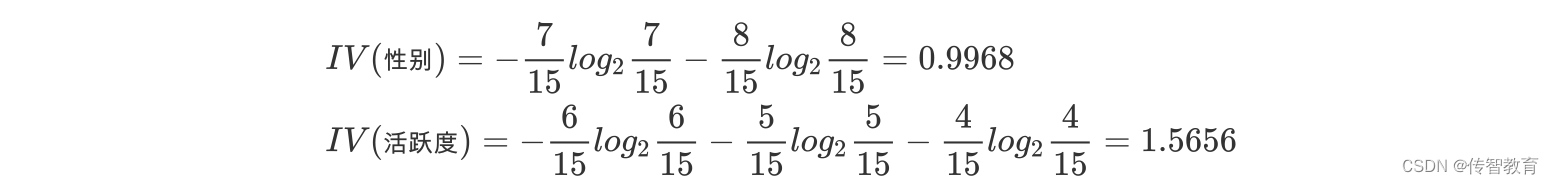
e.计算信息增益率

活跃度的信息增益率更高一些,所以在构建决策树的时候,优先选择
通过这种方式,在选取节点的过程中,我们可以降低取值较多的属性的选取偏好。
案例二
如下图,第一列为天气,第二列为温度,第三列为湿度,第四列为风速,最后一列该活动是否进行。
我们要解决:根据下面表格数据,判断在对应天气下,活动是否会进行?
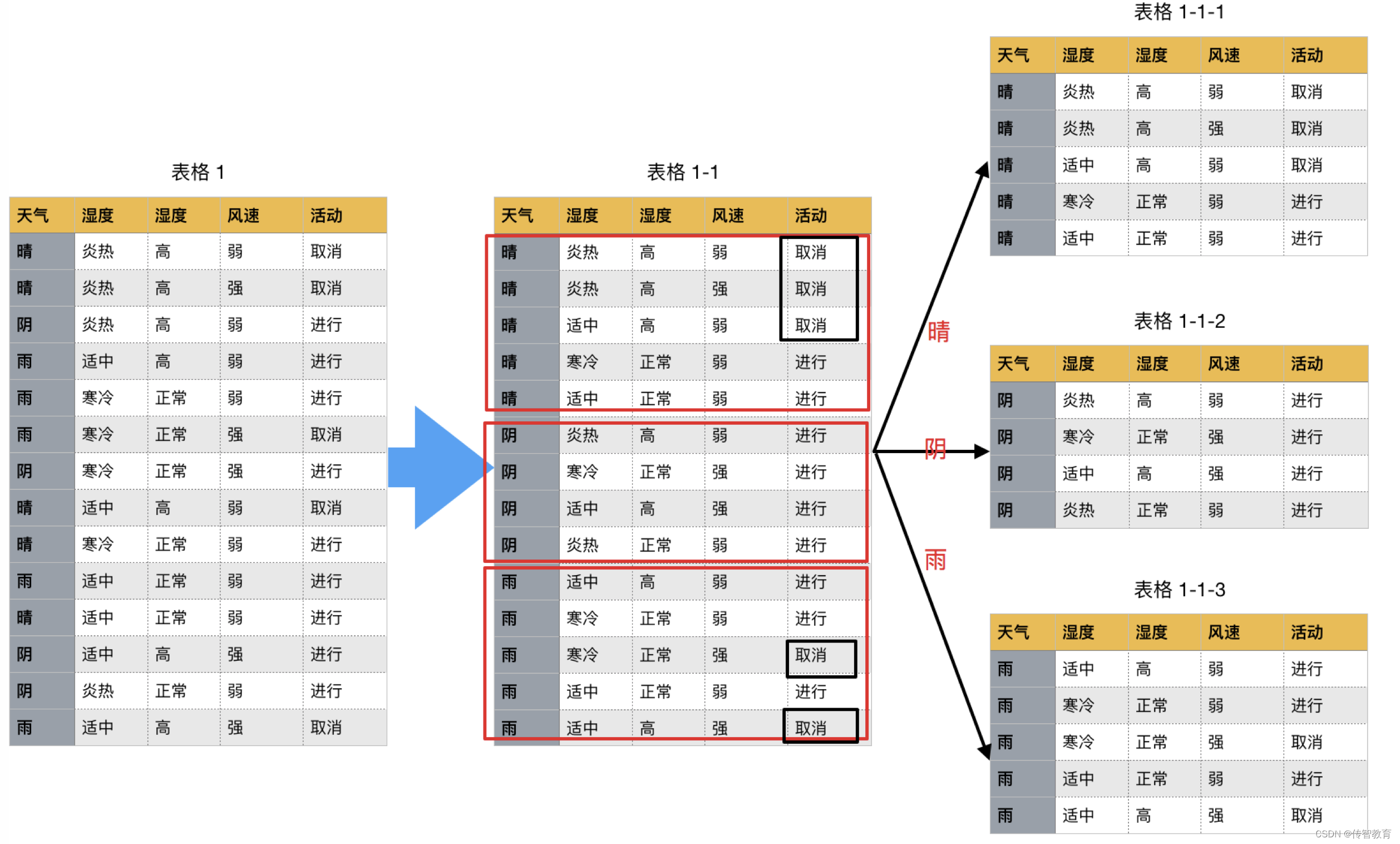

该数据集有四个属性,属性集合A={ 天气,温度,湿度,风速}, 类别标签有两个,类别集合L={进行,取消}。
a.计算类别信息熵
类别信息熵表示的是所有样本中各种类别出现的不确定性之和。根据熵的概念,熵越大,不确定性就越大,把事情搞清楚所需要的信息量就越多。
Ent(D)=−149log2149−145log2145=0.940
b.计算每个属性的信息熵
每个属性的信息熵相当于一种条件熵。他表示的是在某种属性的条件下,各种类别出现的不确定性之和。属性的信息熵越大,表示这个属性中拥有的样本类别越不“纯”。

c.计算信息增益
信息增益的 = 熵 - 条件熵,在这里就是 类别信息熵 - 属性信息熵,它表示的是信息不确定性减少的程度。如果一个属性的信息增益越大,就表示用这个属性进行样本划分可以更好的减少划分后样本的不确定性,当然,选择该属性就可以更快更好地完成我们的分类目标。
信息增益就是ID3算法的特征选择指标。

e.计算信息增益率
天气的信息增益率最高,选择天气为分裂属性。发现分裂了之后,天气是“阴”的条件下,类别是”纯“的,所以把它定义为叶子节点,选择不“纯”的结点继续分裂。
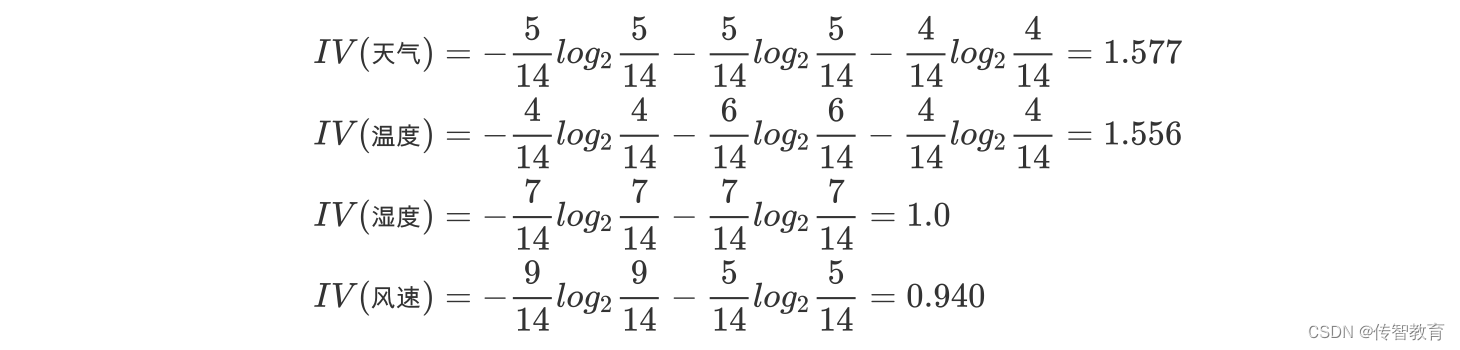
在子结点当中重复过程1~5,直到所有的叶子结点足够"纯"。
现在我们来总结一下C4.5的算法流程
while(当前节点"不纯"):1.计算当前节点的类别熵(以类别取值计算)2.计算当前阶段的属性熵(按照属性取值吓得类别取值计算)3.计算信息增益4.计算各个属性的分裂信息度量5.计算各个属性的信息增益率
end while
当前阶段设置为叶子节点
相关文章:
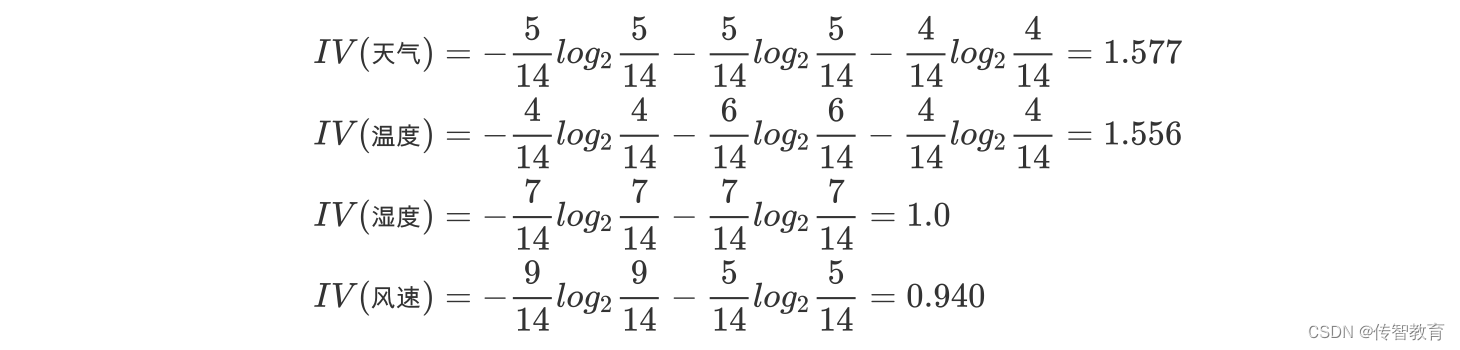
决策树的划分依据之:信息增益率
在上面的介绍中,我们有意忽略了"编号"这一列.若把"编号"也作为一个候选划分属性,则根据信息增益公式可计算出它的信息增益为 0.9182,远大于其他候选划分属性。 计算每个属性的信息熵过程中,我们发现,该属性的值为0, 也就…...

SolidUI社区-独立部署 和 Docker 通信分析
背景 随着文本生成图像的语言模型兴起,SolidUI想帮人们快速构建可视化工具,可视化内容包括2D,3D,3D场景,从而快速构三维数据演示场景。SolidUI 是一个创新的项目,旨在将自然语言处理(NLP)与计算机图形学相…...
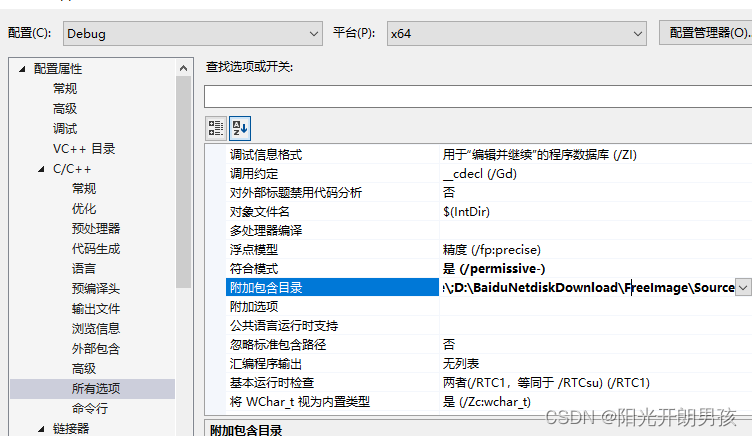
Windows下FreeImage库的配置
首先下载FreeImage库,http://freeimage.sourceforge.net/download.html,官网下载如下: 内部下载地址:https://download.csdn.net/download/qq_36314864/88140305 解压后,打开FreeImage.2017.sln,如果是vs…...
用python编写一个小程序,如何用python编写软件
大家好,给大家分享一下用python编写一个小程序,很多人还不知道这一点。下面详细解释一下。现在让我们来看看! 1、python可以写手机应用程序吗? 我想有人曲解意思了,人家说用python开发渣蔽一个手机app,不是…...

WPF实战学习笔记32-登录、注册服务添加
增加全局账户名同步 增加静态变量 添加文件:Mytodo.Common.Models.AppSession.cs ausing Prism.Mvvm; using System; using System.Collections.Generic; using System.ComponentModel; using System.Linq; using System.Text; using System.Threading.Tasks; us…...
XGBoost的参数
目录 1. 迭代过程 1.1 迭代次数/学习率/初始𝐻最大迭代值 1.1.1 参数num_boost_round & 参数eta 1.1.2 参数base_score 1.1.3 参数max_delta_step 1.2 xgboost的目标函数 1.2.1 gamma对模型的影响 1.2.2 lambda对模型的影响 2. XGBoost的弱评估器 2.…...
【已解决】windows7添加打印机报错:加载Tcp Mib库时的错误,无法加载标准TCP/IP端口的向导页
windows7 添加打印机的时候,输入完打印机的IP地址后,点击下一步,报错: 加载Tcp Mib库时的错误,无法加载标准TCP/IP端口的向导页 解决办法: 复制以下的代码到新建文本文档.txt中,然后修改文本文…...
用于紫外线消毒灯的LED驱动:数明深紫外消毒方案SLM201
用于紫外线消毒灯的LED驱动SLM201 应用于紫外线消毒灯的LED驱动。疫情过后让越来越多的人开始注重起个人健康,除了出门佩戴口罩外,对于居家消毒也越发重视起来。而居家消毒除了75%浓度酒精及各类消毒液外,利用紫外线灯给衣物表面、房间消毒也…...
Docker部署Springboot应用【mysql部署+jar部署+Nginx部署】
【项目达到目标】 1.基本准备 2、mysql部署 3、jar部署 4、Nginx部署 一、基本准备 石工拿的就是之前放置在我们服务器上的应用进行部署,主要就是mysql和jar还有Vue的部署。 目前已经有的是jar、已经打包好的vue 二、mysql部署 docker run -d --name mysql \ …...
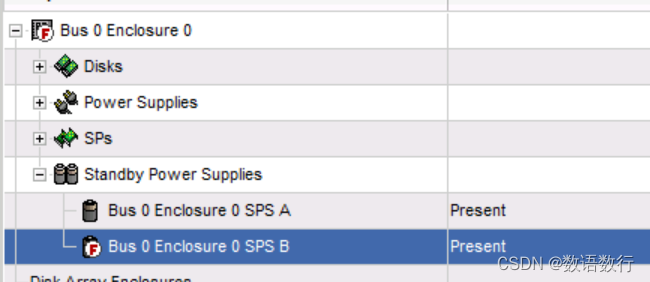
EMC VNX1系列存储电池状态说明
SPS电池正常的状态为“Present”。 SPS电池故障时的状态为“Faulted”。 更换SPS后,SPS开始充电,此时状态显示为“Not Ready”状态。 充电完成后显示为Present状态。如果充电完成后状态前面有“F”标记,则需要重启对应的控制器以更新SPS…...

pyspark 判断 Hive 表是否存在
Catalog.tableExists(tableName: str, dbName: Optional[str] None) → booltableName:表名 dbName:库名(可选) return:bool 值 spark SparkSession \.builder \.appName(tableExists) \.config(spark.num.executors, 6) \.config(spark.executor.memo…...

选择排序算法
选择排序 算法说明与代码实现: 以下是使用Go语言实现的选择排序算法示例代码: package mainimport "fmt"func selectionSort(arr []int) {n : len(arr)for i : 0; i < n-1; i {minIndex : ifor j : i 1; j < n; j {if arr[j] < a…...
快速了解MyBatis---映射关系多对一
文章目录 映射关系多对一映射关系-官方文档映射关系多对1-基本介绍基本介绍注意细节 映射关系多对1-映射方式映射方式配置Mapper.xml 方式-应用实例注解实现多对1 映射-应用实例 映射关系多对一 映射关系-官方文档 文档地址: https://mybatis.org/mybatis-3/zh/sqlmap-xml.ht…...

python学到什么程度算入门,python从入门到精通好吗
本篇文章给大家谈谈python学到什么程度算入门,以及python从入门到精通好吗,希望对各位有所帮助,不要忘了收藏本站喔。 学习 Python 之 进阶学习 一切皆对象 1. 变量和函数皆对象2. 模块和类皆对象3. 对象的基本操作 (1). 可以赋值给变量(2). …...
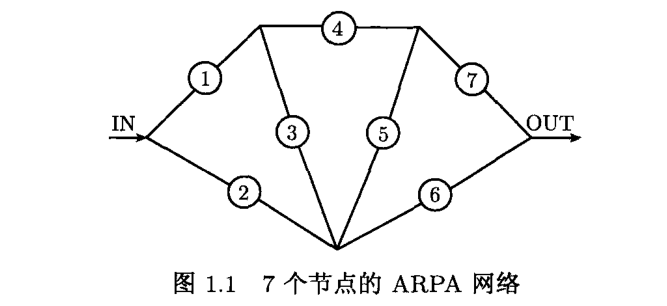
整数规划——第一章 引言
整数规划——第一章 引言 整数规划是带整数变量的最优化问题,即最大化或最小化一个全部或部分变量为整数的多元函数受约束于一组等式和不等式条件的最优化问题。许多经济、管理、交通、通信和工程中的最优化问题都可以用整数规划来建模。 考虑一个电视机工厂的生产…...

C语言结构体讲解
目录 结构体的声明 结构的基础知识 结构的声明 为什么要出现结构体? 结构成员的类型 结构体变量的定义和初始化 定义:(全局变量//局部变量) 初始化: 结构体成员的访问 结构体传参 结构体的声明 结构的基础知识…...
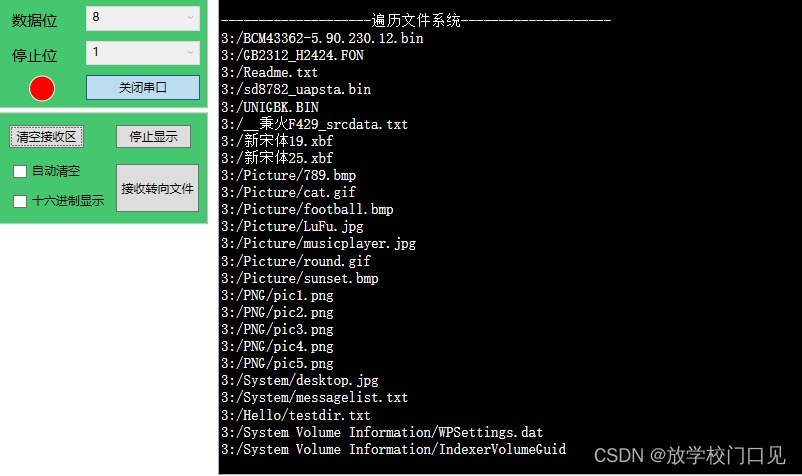
021 - STM32学习笔记 - Fatfs文件系统(三) - 细化与总结
021 - STM32学习笔记 - Fatfs文件系统(三) - 细化与总结 上节内容中,初步实现了FatFs文件系统的移植,并且实现了设备的挂载、文件打开/关闭与读写功能,这里对上节遗留的一些问题进行总结,并且继续完善文件…...
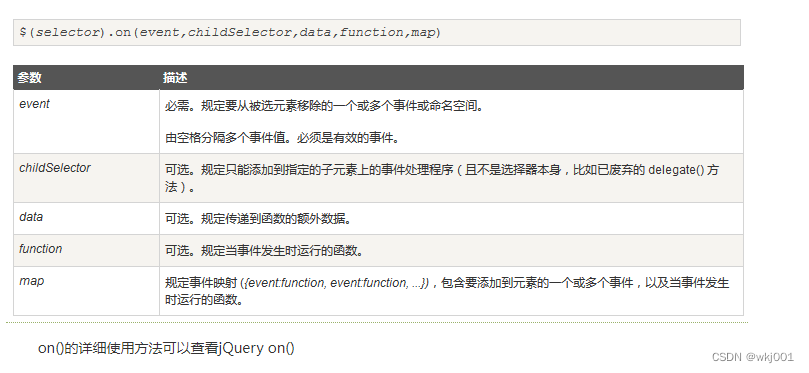
jQuery如何获取动态添加的元素
jQuery如何获取动态添加的元素 使用 on()方法 本质上使用了事件委派,将事件委派在父元素身上 自 jQuery 版本 1.7 起,on() 方法是 bind()、live() 和 delegate() 方法的新的替代品,但是由于on()方法必须有事件,没有事件时可选择de…...
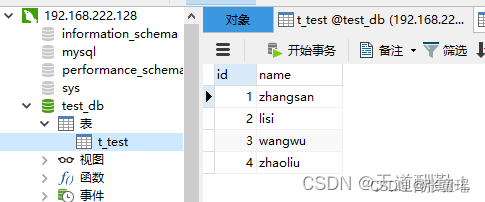
Keepalived 在CentOS 7安装并配置监听MySQL双主
keepalived安装 MySQL双主配置请看这里:https://tongyao.blog.csdn.net/article/details/132016200?spm1001.2014.3001.5502 128、129两台服务器安装步骤相同,配置文件不同,下面有介绍。 1.安装相关依赖包,并下载keepalived安…...

深度学习,神经网络介绍
目录 1.神经网络的整体构架 2.神经网络架构细节 3.正则化与激活函数 4.神经网络过拟合解决方法 1.神经网络的整体构架 ConvNetJS demo: Classify toy 2D data 我们可以看看这个神经网络的网站,可以用来学习。 神经网络的整体构架如下1: 感知器&…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...
