三步问题(力扣)n种解法 JAVA
目录
- 题目:
- 1、dfs:
- 2、dfs + 备忘录(剪枝):
- (1)神器 HashMap 备忘录:
- (2)数组 memo 备忘录:
- 3、动态规划:
- 4、利用 static 的储存功能:
- (1)static 修饰 HashMap:
- (2)static 修饰 memo 数组:
- (3)static 修饰 dp 数组 + 动态规划:
- 5、动态规划 + 优化常数空间:
- 6、数学 矩阵:
题目:
三步问题。有个小孩正在上楼梯,楼梯有n阶台阶,小孩一次可以上1阶、2阶或3阶。实现一种方法,计算小孩有多少种上楼梯的方式。结果可能很大,你需要对结果模1000000007。
示例1:
输入:n = 3
输出:4
说明: 有四种走法
示例2:
输入:n = 5
输出:13
提示:
n范围在[1, 1000000]之间
解题思路:
记得多次取模防止爆掉int
1、dfs:
class Solution {int INF = 1000000007;public int waysToStep(int n) {return dfs(n) % INF;}public int dfs(int n) {if(n < 0) return 0;if(n == 0) return 1;return ((dfs(n - 1) + dfs(n - 2)) % INF + dfs(n - 3)) % INF;}
}

显然超时,得剪枝
2、dfs + 备忘录(剪枝):
(1)神器 HashMap 备忘录:
class Solution {int INF = 1000000007;Map<Integer, Integer> map = new HashMap<>();public int waysToStep(int n) {map.put(0, 1);return dfs(n) % INF;}public int dfs(int n) {if(n < 0) return 0;if(map.containsKey(n)) return map.get(n);int ans = ((dfs(n - 1) + dfs(n - 2)) % INF + dfs(n - 3)) % INF;map.put(n, ans);return ans;}
}


当然神器也是有缺陷的即查询需要些许时间,可以试试用数组当备忘录
(2)数组 memo 备忘录:
class Solution {int INF = 1000000007;public static int memo[];public int waysToStep(int n) {memo = new int[n + 1];memo[0] = 1;return dfs(n) % INF;}public int dfs(int n) {if(n < 0) return 0;if(memo[n] != 0) return memo[n];int ans = ((dfs(n - 1) + dfs(n - 2)) % INF + dfs(n - 3)) % INF;memo[n] = ans;return memo[n];}
}


速度快了不少,还有突破空间
3、动态规划:
代码:
class Solution {public int waysToStep(int n) {if(n <= 2) return n;if (n == 3) return 4;int[] d = new int[n + 1];d[1] = 1;d[2] = 2;d[3] = 4;for (int i = 4; i <= n; i++){d[i] = (d[i-1] + d[i-2]) % 1000000007 +d[i-3];d[i] %= 1000000007;}return d[n];}
}


不太理解为什么会比 dfs + 剪枝快这么多,这里给出的猜测是递归压栈耗费了大量时间
当然26ms还有突破空间
4、利用 static 的储存功能:
之前提到过Java的static修饰变量是有存储功能的不会因为创建新对象就恢复初始化
static简述 JAVA
(1)static 修饰 HashMap:
代码:
class Solution {int INF = 1000000007;public static Map<Integer, Integer> map = new HashMap<>();public int waysToStep(int n) {map.put(0, 1);return dfs(n);}public int dfs(int n) {if(n < 0) return 0;if(map.containsKey(n)) return map.get(n);int ans = ((dfs(n - 1) + dfs(n - 2)) % INF + dfs(n - 3)) % INF;map.put(n, ans);return ans;}
}


时间大概降了一半
(2)static 修饰 memo 数组:
为了更好储存memo数组要设置最大长度
代码:
class Solution {int INF = 1000000007;public static int memo[] = new int[1000001];public int waysToStep(int n) {memo[0] = 1;return dfs(n) % INF;}public int dfs(int n) {if(n < 0) return 0; if(memo[n] != 0) return memo[n];int ans = ((dfs(n - 1) + dfs(n - 2)) % INF + dfs(n - 3)) % INF;memo[n] = ans;return memo[n];}
}


速度也是之前的一半
(3)static 修饰 dp 数组 + 动态规划:
充分利用了动态规划的高效以及static的存储功能设立static变量j避免重复更新数据
代码:
class Solution {public static int dp[] = new int[1000000];public static int j;public int waysToStep(int n) { if(dp[n] != 0) return dp[n];if(n <= 2) return n;if (n == 3) return 4;if(j < 3){dp[0] = 1;dp[1] = 1;dp[2] = 2;dp[3] = 4;j = 4;} for (int i = j; i <= n; i++) dp[i] = ((dp[i-1] + dp[i-2]) % 1000000007 +dp[i-3]) % 1000000007;j = n;return dp[n];}
}


偶然能触及12ms的边边
5、动态规划 + 优化常数空间:
代码:
class Solution {public int waysToStep(int n) {if (n == 1) return 1;if (n == 2) return 2;if (n == 3) return 4;long a = 1, b = 2, c = 4, d;while (--n >= 3) {d = a + b + c;a = b;b = c;c = d % 1000000007;}return (int) c;}
}


这是网上大佬写的也这么快是我没想到的
目前猜测唯一可能是static修饰变量每次创建新对象仍要创建一次数组,且创建数组需要耗费很多时间
6、数学 矩阵:
class Solution {public static int waysToStep(int n) {if (n == 1) {return 1;}if (n == 2) {return 2;}if (n == 3) {return 4;}long[][] m = {{1, 1, 1}, {1, 0, 0}, {0, 1, 0}};long[][] mn = pow(m, n - 3);long res = (mn[0][0] * 4 + mn[0][1] * 2 + mn[0][2] * 1) % 1000000007;return (int) res;}public static long[][] pow(long[][] a, int i) {long[][] val = {{1, 0, 0}, {0, 1, 0}, {0, 0, 1}};while (i != 0) {if ((i % 2) == 1) {val = multiply(val, a);}a = multiply(a, a);i = i / 2;}return val;}public static long[][] multiply(long[][] a, long[][] b) {long[][] c = new long[3][3];for (int i = 0; i < 3; i++) {for (int j = 0; j < 3; j++) {long s = 0;for (int k = 0; k < 3; k++) {s = (s + (a[i][k] % 1000000007 * b[k][j] % 1000000007)) % 1000000007;}c[i][j] = s % 1000000007;}}return c;}
}
网上大佬写的,真快,给我看傻了
相关文章:

三步问题(力扣)n种解法 JAVA
目录 题目:1、dfs:2、dfs 备忘录(剪枝):(1)神器 HashMap 备忘录:(2)数组 memo 备忘录: 3、动态规划:4、利用 static 的储存功能:&…...

flask---》登录认证装饰器/配置文件/路由系统
登录认证装饰器 # 0 装饰器的本质原理-# 类装饰器:1 装饰类的装饰器 2 类作为装饰器 # 1 装饰器使用位置,顺序 # 3 flask路由下加装饰器,一定要加endpoint-如果不指定endpoint,反向解析的名字都是函数名,不加装饰器…...
)
Jvm实际运行情况-JVM(十七)
上篇文章说jmap和jstat的命令,如何查看youngGc和FullGc耗时和次数。 Jmap-JVM(十六) Jvm实际运行情况 背景: 机器配置:2核4G JVM内存大小:2G 系统运行天数:7天 期间发生FULL GC次数和耗时…...
【BASH】回顾与知识点梳理(二)
【BASH】回顾与知识点梳理 二 二. Shell 的变量功能2.1 什么是变量?2.2 变量的取用与设定: echo, 变量设定规则: set/unset2.3 环境变量的功能用 set 观察所有变量 (含环境变量与自定义变量)export: 自定义变量转成环境变量那如何将环境变量转成自定义变…...

【分布式训练】Accelerate 多卡训练,单卡评测,进程卡住的解决办法
最近想把之前的一个模型的改成多卡训练的。我并不懂DDP,DP。一开始打算使用Transformers的Trainer,但是配置的过程踩了很多坑也没有弄成功。【我是自己写的评测方法,但是我找不到能让触发Trainer去用我的方法评测的路劲】,后来偶然…...

时间复杂度为O(nlogn)的两种排序算法
1.归并排序 归并排序的核心思想:如果要排序一个数组,我们先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排好序的两部分合并在一起,这样整个数组就都有序了。 归并排序使用的就是分治思想。分治&#x…...

java调用onnx模型,支持yolov5和yolov7
不点star不给解答问题 可直接运行主文件:ObjectDetection_1_25200_n.java 或者 ObjectDetection_n_7.java 都可以直接运行两个可以运行的主文件是为了支持不用网络结构的模型,即使是onnx模型,输出的结果参数也不一样,支持以下两种…...
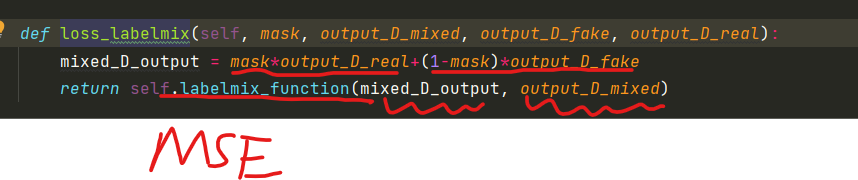
DP-GAN损失
在前面我们看了生成器和判别器的组成。 生成器损失公式: 首先将fake image 和真实的 image输入到判别器中: 接着看第一个损失:参数分别为fake image经过判别器的输出mask,和真实的label进行损失计算。对应于: 其中l…...

自监督去噪:Noise2Void原理和调用(Tensorflow)
文章原文: https://arxiv.org/abs/1811.10980 N2V源代码: https://github.com/juglab/n2v 参考博客: https://zhuanlan.zhihu.com/p/445840211https://zhuanlan.zhihu.com/p/133961768https://zhuanlan.zhihu.com/p/563746026 文章目录 1. 方法原理1.1 Noise2Noise回…...
Mac 安装配置adb命令环境(详细步骤)
一、注意:前提要安装java环境。 因为android sdk里边开发的一些包都是依赖java语言的,所以,首先要确保已经配置了java环境。 二、在Mac下配置android adb命令环境,配置方式如下: 1、下载并安装IDE (andr…...
 GDALRasterBand篇 代码示例 翻译 自学)
GDAL C++ API 学习之路 (2) GDALRasterBand篇 代码示例 翻译 自学
GDALRasterBand Class <gdal_priv.h> GDALRasterBand是GDAL中用于表示栅格数据集中一个波段的类。栅格数据集通常由多个波段组成,每个波段包含了特定的数据信息,例如高程、红、绿、蓝色等, 用于表示影像的不同特征。提供了许…...

springboot对静态资源的支持
1、spring boot默认静态路径支持 Spring Boot 默认将 / 所有访问映射到以下目录:** classpath:/static classpath:/public classpath:/resources classpath:/META-INF/resources也就是说什么也不用配置,通过浏览器可以直接访问这几个目录下的文件。 1…...

WPF实战学习笔记27-全局通知
新建消息事件 添加文件:Mytodo.Common.Events.MessageModel.cs using Prism.Events; using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; using System.Windows.Diagnostics;namespace Mytod…...

openSUSE安装虚拟化 qemu kvm
1) 第一种:图形界面yast安装虚拟化 左下角开始菜单搜索yast 点一下就能安装,是不是很简单呢 2)第二种: 命令行安装 网上关于openSUSE安装qemu kvm的教程比较少,可以搜索centos7 安装qemu kvm的教程,然后…...
基于linux下的高并发服务器开发(第四章)- 多进程实现并发服务器(回射服务器)
1. socket // 套接字通信分两部分: - 服务器端:被动接受连接,一般不会主动发起连接 - 客户端:主动向服务器发起连接 2.字节序转换函数 当格式化的数据在两台使用不同字节序的主机之间直接传递时,接收端必然错误…...

【程序分析】符号执行
符号执行入门 参考:https://zhuanlan.zhihu.com/p/26927127 给定一个结果,求解对应的程序输入。 经典符号执行与动态符号执行 参考:https://p1kk.github.io/2021/04/04/others/%E7%AC%A6%E5%8F%B7%E6%89%A7%E8%A1%8C&%E6%B1%A1%E7%82…...

实验笔记之——Windows下的Android环境开发搭建
好久一段时间没有进行Android开发了,最新在用的电脑也没有了Android studio了。为此,本博文记录一下最近重新搭建Android开发的过程。本博文仅为本人学习记录用(**别看) 之前博客也对配置Android做过记录 Android学习笔记之——A…...

#rust taur运行报错#
场景:在window11系统上运行 tauri桌面莹应用,提示错误。 Visual Studio 2022 生成工具 安装的sdk11 , rust运行模式是stable-x86_64-pc-window-gnu, 运行npm run tauir dev 一致失败,失败信息如下 原因:1:在window11系…...

学习购药系统源码:从前端到后端的技术探索
本文将带领读者探索购药系统源码,从前端到后端逐步深入,了解其核心功能和实现方式。我们将使用常见的Web技术,包括HTML、CSS、JavaScript、以及Python的Django框架,展示购药系统的技术奥秘。 前端技术探索 HTML结构搭建 购药系…...

第九次CCF计算机软件认证
第一题:中间数 在一个整数序列 a1,a2,…,an 中,如果存在某个数,大于它的整数数量等于小于它的整数数量,则称其为中间数。 在一个序列中,可能存在多个下标不相同的中间数,这些中间数的值是相同的。 给定一个…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...
