OpenMP
官方文档:OpenMP | LLNL HPC Tutorials
OpenMP总览
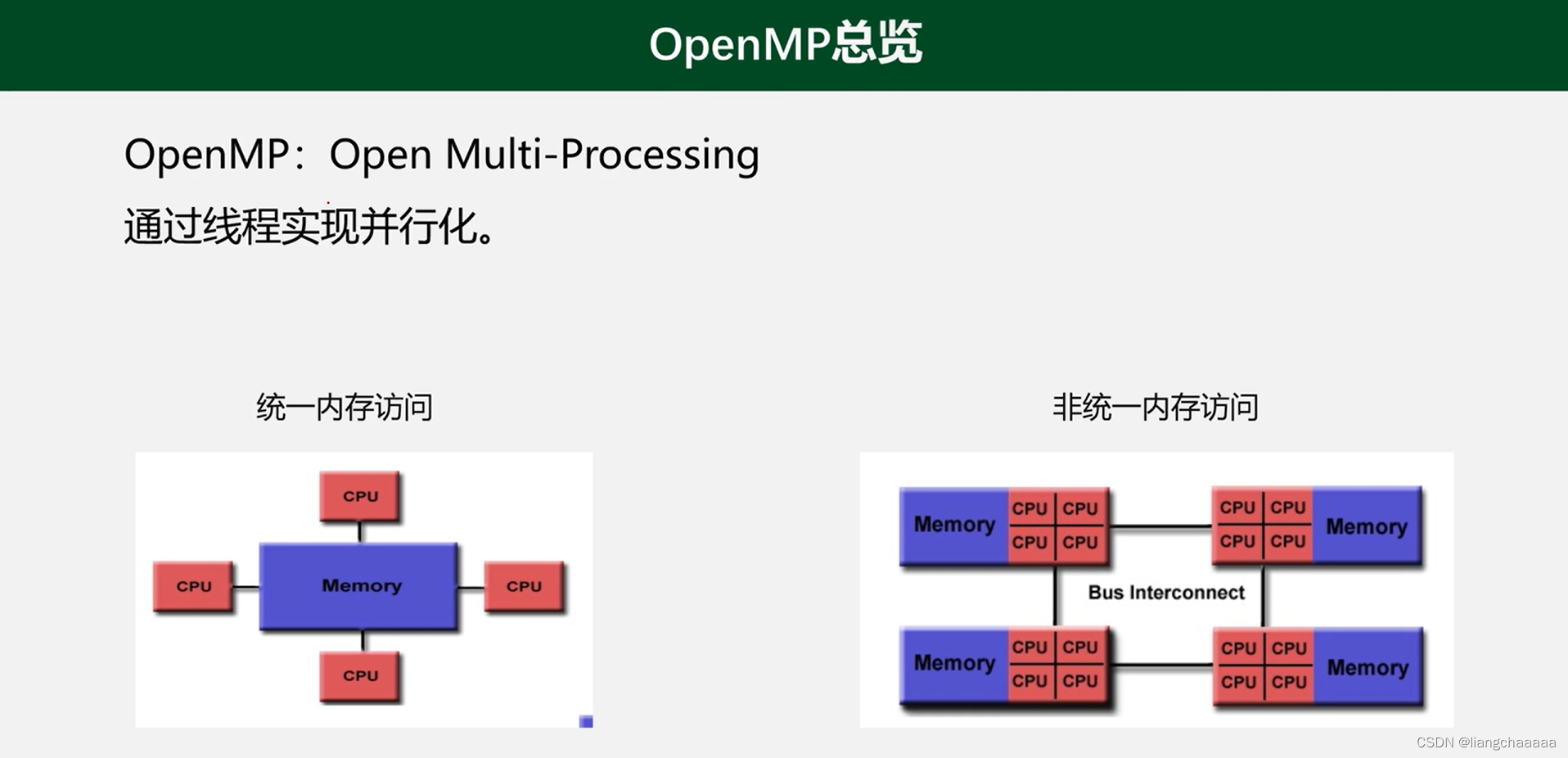
统一内存访问:OpenMP、Pthreads
非统一内存访问:MPI
OpenMP与Pthread

OpenMP原理
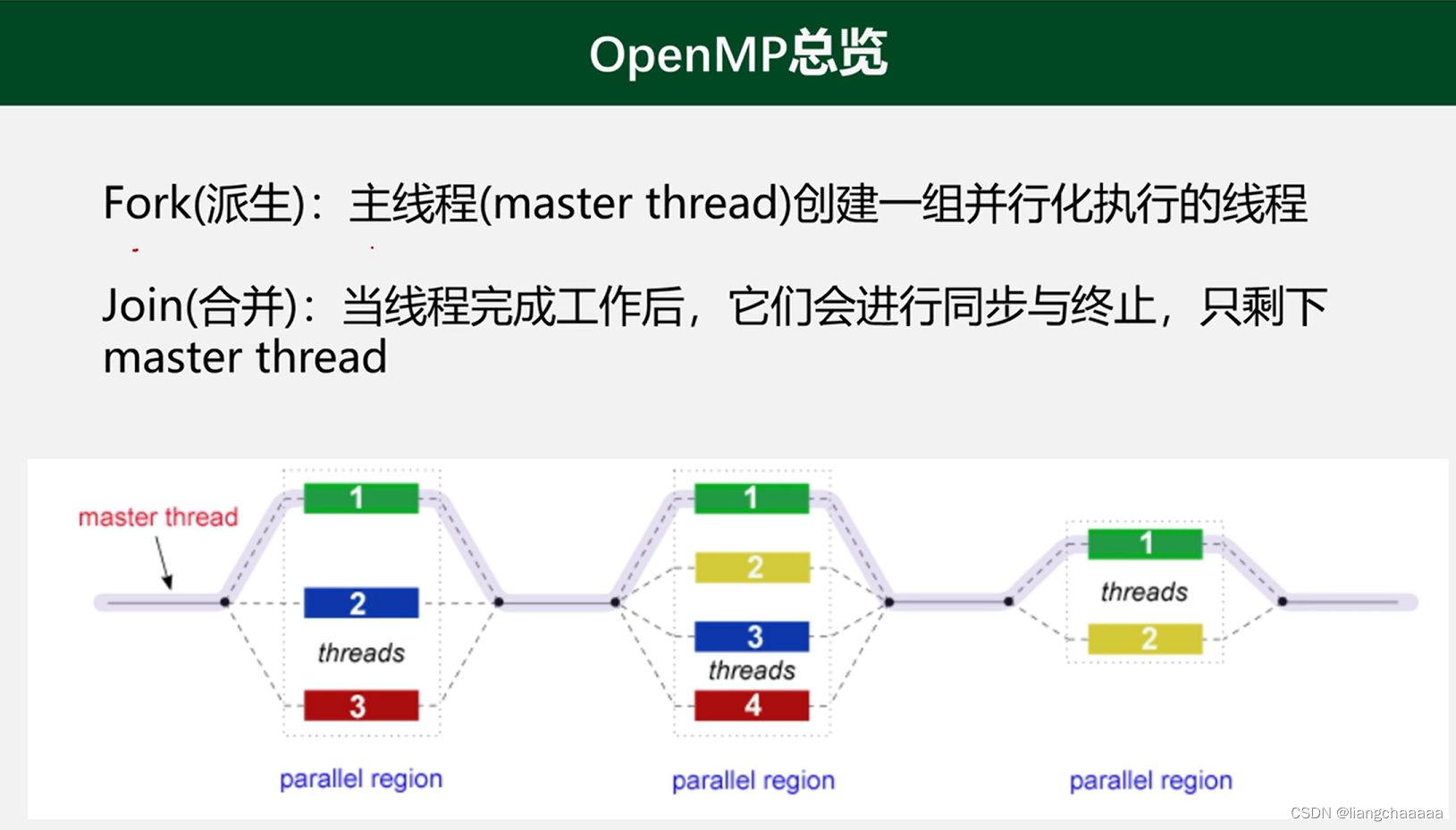
串行区到达并行区后会派生多个线程,并行区代码执行完后进行线程合并,剩下主线程
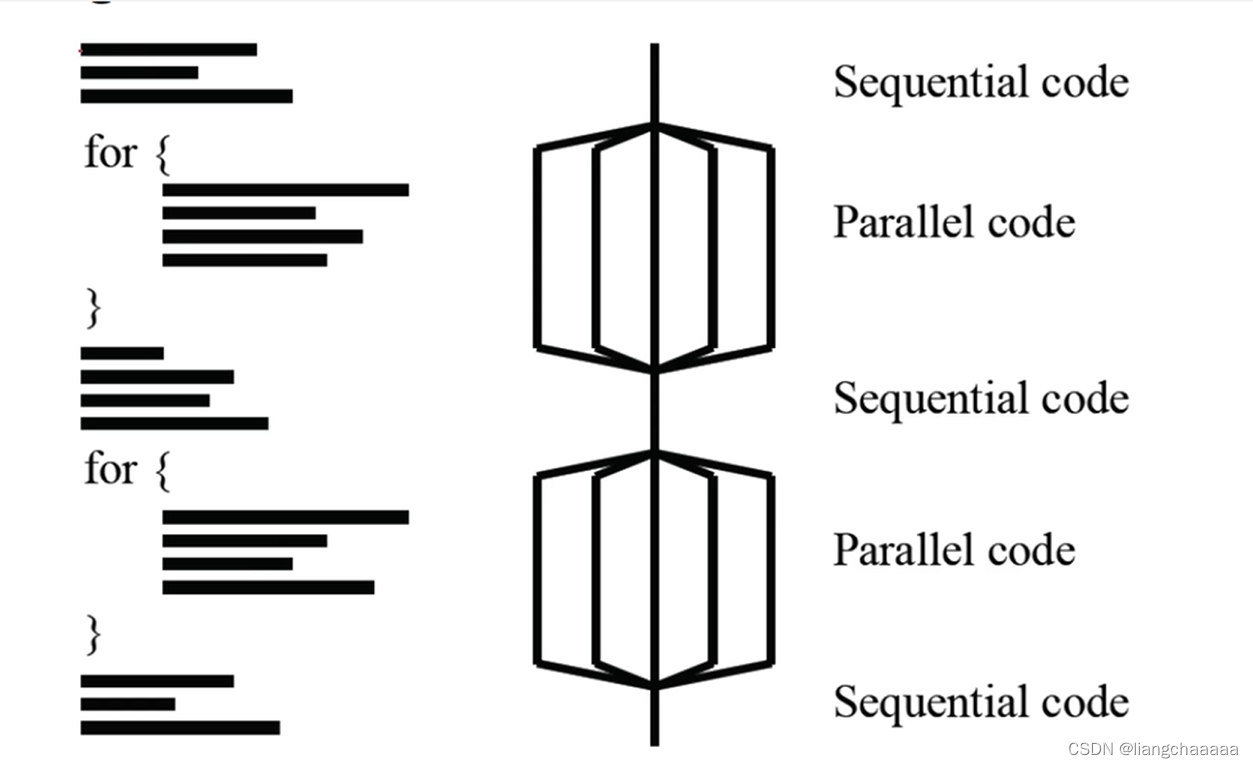
编译指导语句格式
openmp提供基于指令的内存共享API
预处理指令:#pragma omp 指导指令 [子句]
若一行放不下要另起一行,则需要 / 来转义
编译指令:gcc -g -fopenmp -o hello hello.c
没有代码补全了,很急啊!!!
示例程序
“Hello world”
#include<stdlib.h>
#include<stdio.h>
#ifdef _OPENMP
#include<omp.h>
#endifint thread_count;
void* Hello(void)
{#ifdef _OPENMPint my_rank = omp_get_thread_num();//获取线程号int thread_count = omp_get_num_threads();//确定当前线程组中活动线程的数量#elseint my_rank = 0;int thread_count = 1;#endifprintf("Hello from thread %ld of %d\n",my_rank,thread_count);return NULL;
}int main(int argc,char* argv[])
{thread_count = strtol(argv[1],NULL,10);#pragma omp parallel num_threads(thread_count)Hello();return 0;
}不传惨默认电脑核数(我的电脑是12核)
计算机环境变量:OMP_NUM_THREADS
传参结果

梯形积分法
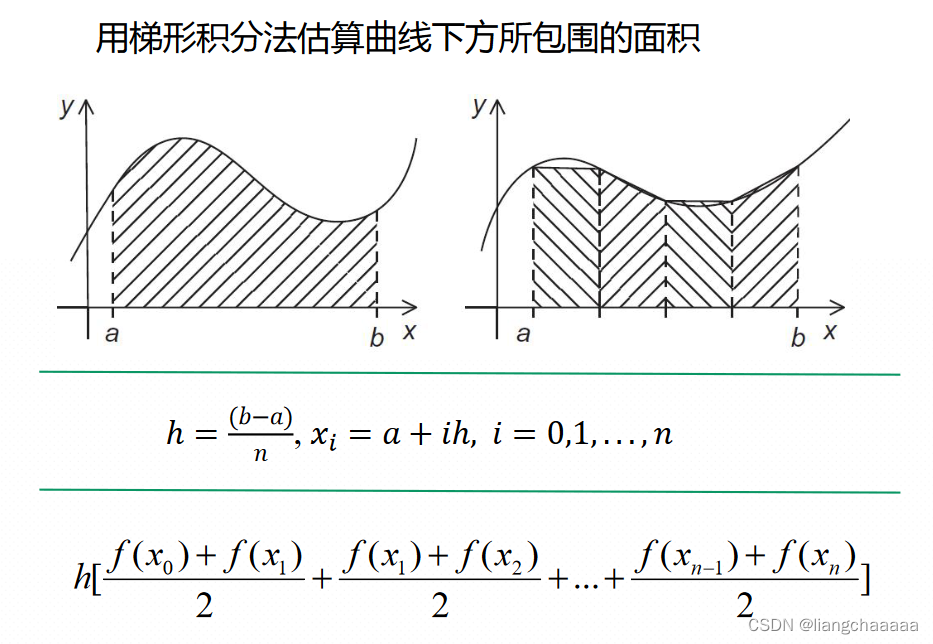
#include<stdlib.h>
#include<stdio.h>
#include<math.h>
#ifdef _OPENMP
#include<omp.h>
#endifvoid work(double a,double b,int n,double *global_result)
{#ifdef _OPENMPint my_rank = omp_get_thread_num();//获取线程号int thread_count = omp_get_num_threads();//确定当前线程组中活动线程的数量#elseint my_rank = 0;int thread_count = 1;#endifdouble h = (b-a)/n;double my_result;int local_n = n/thread_count;//每个线程执行多少块梯形double local_a = a + my_rank * local_n * h;double local_b = local_a + local_n * h;long long i;my_result = (sin(local_a)+sin(local_b))/2.0;for(i=1;i<=local_n-1;i++){//这里ppt写的是i<loacl_n-1,应该是<=double x = (double)i*h + local_a;my_result += sin(x);}my_result *= h;#pragma omp critical{*global_result += my_result;}}int main(int argc,char* argv[])
{ int thread_count;int n;//分割成n个梯形double a,b;//积分区域的左右两端double global_result = 0.0;thread_count = strtol(argv[1],NULL,10);printf("Please enter n,a and b\n");scanf("%d %lf %lf",&n,&a,&b);#pragma omp parallel num_threads(thread_count)work(a,b,n,&global_result);printf("result: %.6f",global_result);return 0;
}变量作用域
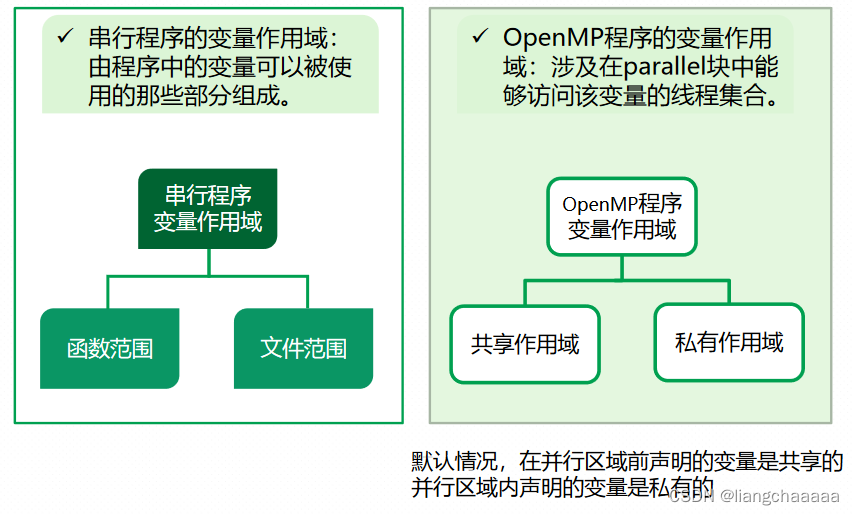
private ( list )
private将一个或多个变量声明成线程的私有变量,每个线程有自己变量私有副本,仅当前并行区域有效 。
fistprivate ( list )
对私有变量进行初始化,把串行变量值拷贝到私有变量中。
lastprivate ( list )
对私有变量的终结操作,把私有变量(最后的循环迭代)拷贝到同名串行变量中。shared ( list )
将变量声明为共享变量

上面为粗粒度锁,下面为细粒度锁
double factor = 1.0;
double sum = 0.0;
# pragma omp parallel for num_threads( th_count ) default(none) reduction( +: sum ) \
private( k, factor ) shared(n)
for ( k = 0; k < n; k ++ ) {
if ( k % 2 == 0)
factor = 1.0;
else
factor = -1.0;
sum += factor / ( 2 * k + 1 );
}
pi_approx = 4.0 * sum;default(none) 相当于在并行区域之前告诉编译器,在没有使用 shared 或 private 等指定变量共享属性的情况下,所有变量都被视为私有的。这样做是为了防止程序员忘记明确指定共享属性导致错误的结果。
归约子句
归约操作将归约操作符重复地应用于操作数序列来得到一个结果的计算
语法:reduction ( <operator> : <variable list>)

global_result = 0.0;
# pragma omp parallel num_threads (thread_count) reduction (+: global_result)
global_result += Local_trap(a,b,n);把各个线程计算的结果汇总到归约变量上
归约是通过为每个隐式任务创建每个线程的列表项的私有副本来实现的,就像使用了private子句global_result += my_result一样。
OpenMP for
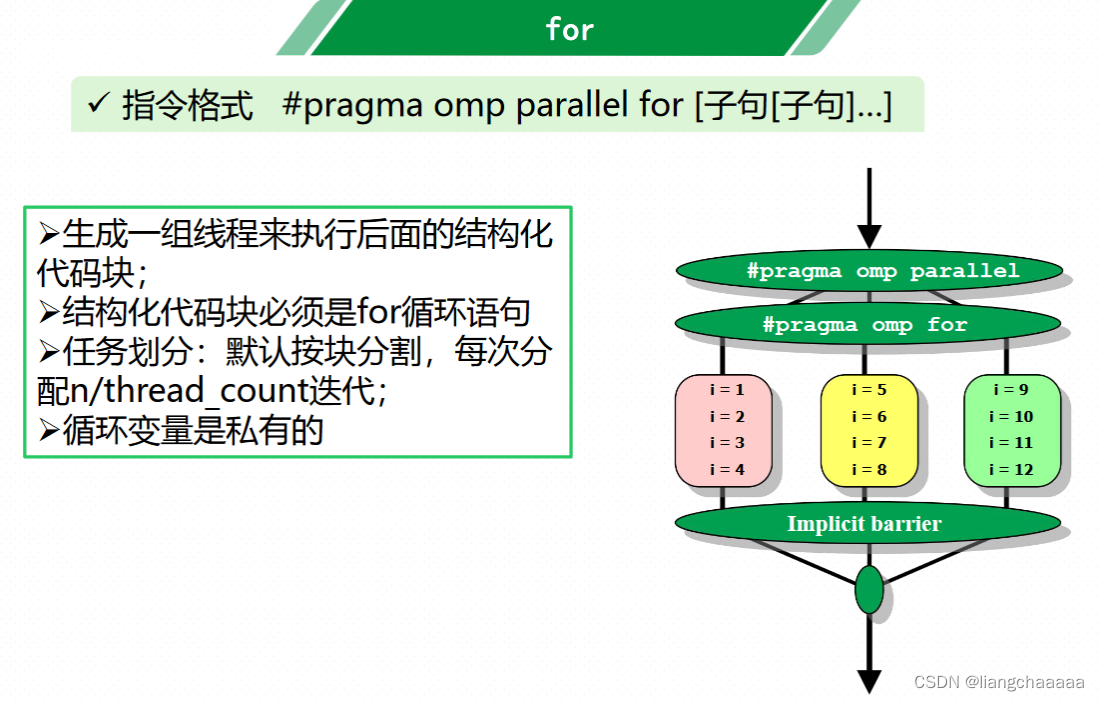
它告诉编译器,接下来的for循环将会使用并行的方式执行
使用并行的时候需要满足以下四个需求:
在循环的迭代器必须是可计算的并且在执行前就需要确定迭代的次数。
在循环的代码块中不能包含break,return,exit。
在循环的代码块中不能使用goto跳出到循环外部。
迭代器只能够被for语句中的增量表达式所修改。
嵌套循环并行化中内层循环并行和外层循环并行是不一样的
以下为2个线程为例:
1.外层:
i = 0时为一个线程,i = 1为一个线程,每个线程执行一次j = 6,7,8,9
因为是并行,所以会有i = 0和i = 1交替出现的情况,同时需要用private将j声明成线程私有变量,因为i = 0时的j和i = 1时的j不一样
2.内层:
j = 6,9为一个线程,j = 8,7为一个线程,不需要private声明,开启并行区域时,两个线程的i索引都相同,用的是同一层i下的j
 数据依赖性
数据依赖性
OpenMP编译器不检查被parallel for指令并行化的循环所包含的迭代间的依赖关系
一个或者更多个迭代结果依赖于其他迭代的循环,一般不能被正确的并行化有数据依赖关系的计算被分配到一个线程,不会影响计算结果
比如在斐波那契数列,算了前面的才能算后面的,但是parallel for会把n次迭代分配好后同时开始算,并不会等计算下标在前的数的线程算好后再算
OpenMP section and single


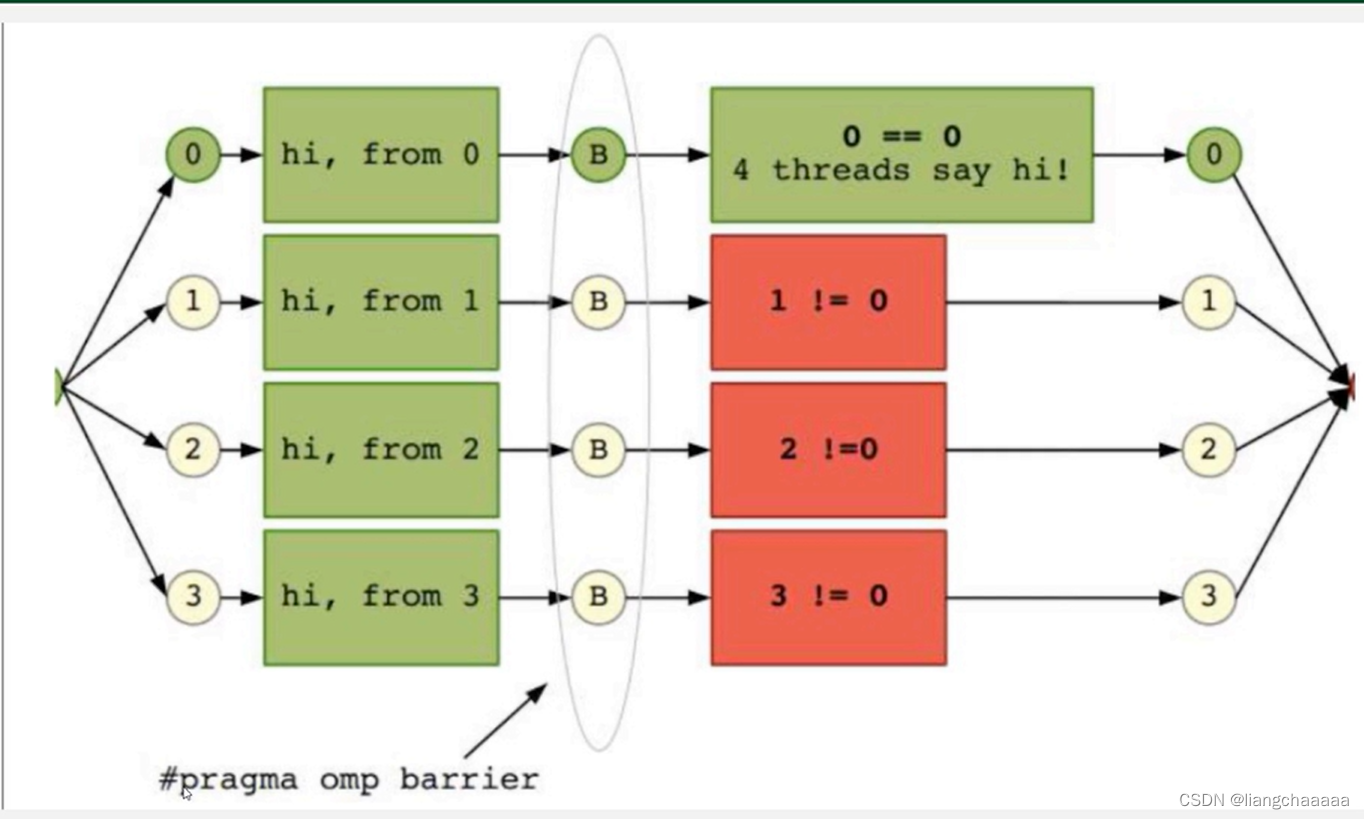
OpenMP barrier

循环调度




相关文章:

OpenMP
官方文档:OpenMP | LLNL HPC Tutorials OpenMP总览 统一内存访问:OpenMP、Pthreads 非统一内存访问:MPI OpenMP与Pthread OpenMP原理 串行区到达并行区后会派生多个线程,并行区代码执行完后进行线程合并,剩下主线程 编…...

Eureka 学习笔记4:EurekaClient
版本 awsVersion ‘1.11.277’ EurekaClient 接口实现了 LookupService 接口,拥有唯一的实现类 DiscoveryClient 类。 LookupService 接口提供以下功能: 获取注册表根据应用名称获取应用根据实例 id 获取实例信息 public interface LookupService<…...

前端后端路径问题详解
加了项目名,访问所有页面都是 在 项目名下 出来的路径 不加项目名,访问所有页面都不用加项目名,然后前后端的加/的效果都一样,都是在根目录下没有项目名的路径!!! 后端 一、MVC 1.不管是转发…...

@vue/composition-api原理解析
前言 上一篇文章介绍了vue/composition-api是什么,以及为什么要用,现在来系统地解析一下 vue/composition-api 的实现原理,希望可以加深对其工作机制的理解。 老规矩先分享下AI评价:对vue/composition-api实现原理的介绍整体上非…...
从入门到精通系列之三:K8s的基本概念和术语之资源对象概述)
Kubernetes(K8s)从入门到精通系列之三:K8s的基本概念和术语之资源对象概述
Kubernetes K8s从入门到精通系列之三:K8s的基本概念和术语之资源对象概述 K8s中的基本概念和术语大多是围绕资源对象(Resource Object)来说的,而资源对象在总体上可分为以下两类: 某种资源的对象,例如节点(Node)、Pod、服务(Serv…...

cc2652在使用过程中的一些注意事项
可能不只是cc2652有这些坑,估计cc26xx系列都存在。 CCS的预编译宏配置位置 时钟获取 时钟获取__STATIC_INLINE uint32_t SysCtrlClockGet( void )在sys_ctrl.h中,sys_ctrl.h没有在工程路径下面,在其sdk中 节拍时间获取 ICall_getTicks(); …...

YAPI接口自动鉴权功能部署详解
目录 安装准备 在线安装 离线安装 配置使用 安装准备 以下操作,默认要求自己部署过yapi,最好是部署过yapi二次开发环境。 无论是选择在线安装或者是本地安装,都需要安装client工具。 1、yapi-cli:npm install yapi-cli –g…...

【雕爷学编程】Arduino动手做(180)---Seeeduino Lotus开发板3
37款传感器与执行器的提法,在网络上广泛流传,其实Arduino能够兼容的传感器模块肯定是不止这37种的。鉴于本人手头积累了一些传感器和执行器模块,依照实践出真知(一定要动手做)的理念,以学习和交流为目的&am…...
)
搜索与图论(二)
最短路 单源最短路 所有边权都是正数 朴素Dijkstra算法 基本思路:从1号点到其他点的最短距离 步骤: 定义一个s集合包含当前已确定最短距离的点 1、初始化距离dis[1] 0,dis[其它] 正无穷 2、for i 0-n循环n次 2.1找到不在s中的距离最近的点 ->t 2.2把t加到s当中去…...
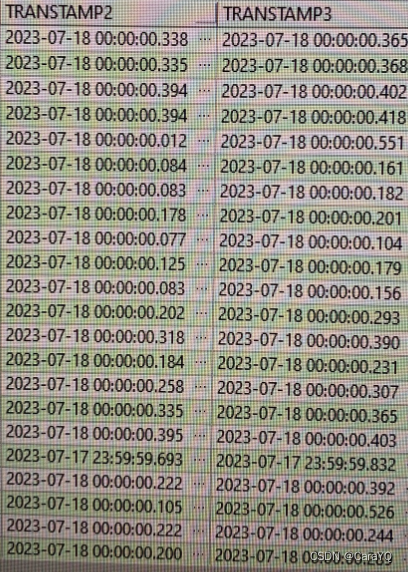
【SQL】-【计算两个varchar类型的timestamp的毫秒差】
背景 TRANSTAMP3、TRANSTAMP2在Oracle数据库中的类型为varchar,但实际保存的值是时间戳timestamp类型,现在要计算二者的毫秒差 Oracle或MySQL extract(second from (to_timestamp(TRANSTAMP3,yyyy-mm-dd hh24:mi:ss.ff) - to_timestamp(TRANSTAMP2,yyy…...
)
Java 微信商家打款到零钱(旧版本接口)
旧版微信支付接口要求请求时携带证书请求 构建请求参数 /*** 付款到零钱** param withdrawalDto dto撤军* return {link Map }<{link String }, {link Object }>* throws Exception 异常* Author chen 2023-07-27 15:04*/private Map<String, Object> payToUser(Wi…...

Vue+Element ui Study
目录 一、VueElement ui 1、show-overflow-tooltip属性设置宽度 2、this.$refs使用方法 Error in v-on handler: “TypeError: Cannot read properties of undefined (reading ‘xxx‘)“ 一、VueElement ui 1、show-overflow-tooltip属性设置宽度 :show-overflow-toolti…...
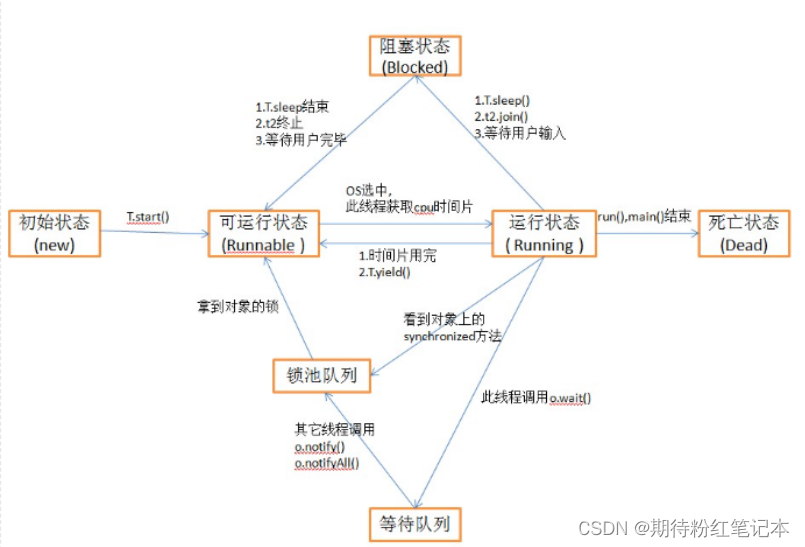
JAVA基础-多线程入门(详解)
目录 引言 一,线程概念 二,创建线程 2.1,继承Thread类,重写run方法 2.2,实现Runnable接口,重写run方法,实现Runnable接口的实现类的实例对象作为Thread构造函 数的target 2.3,通…...

Cirno‘s Perfect Equation Class 2023牛客暑期多校训练营5 D
登录—专业IT笔试面试备考平台_牛客网 题目大意:有q次询问,每次给出三个整数k,c,n,求有多少满足条件的数对(a,b)满足kabc且c是b的倍数,且gcd(a,b)>n 1<q<100;…...
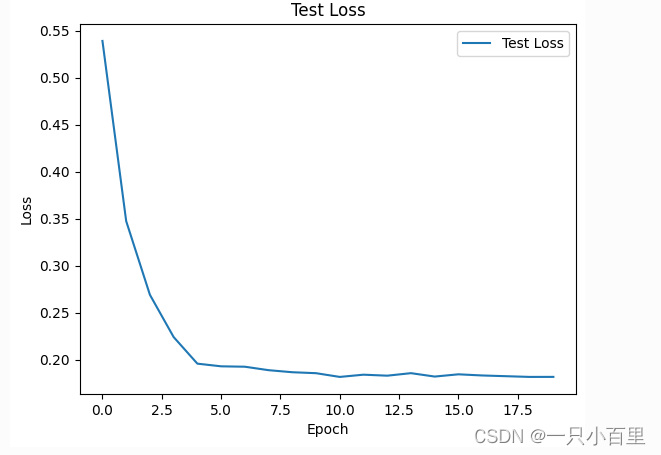
pytorch学习——如何构建一个神经网络——以手写数字识别为例
目录 一.概念介绍 1.1神经网络核心组件 1.2神经网络结构示意图 1.3使用pytorch构建神经网络的主要工具 二、实现手写数字识别 2.1环境 2.2主要步骤 2.3神经网络结构 2.4准备数据 2.4.1导入模块 2.4.2定义一些超参数 2.4.3下载数据并对数据进行预处理 2.4.4可视化数…...
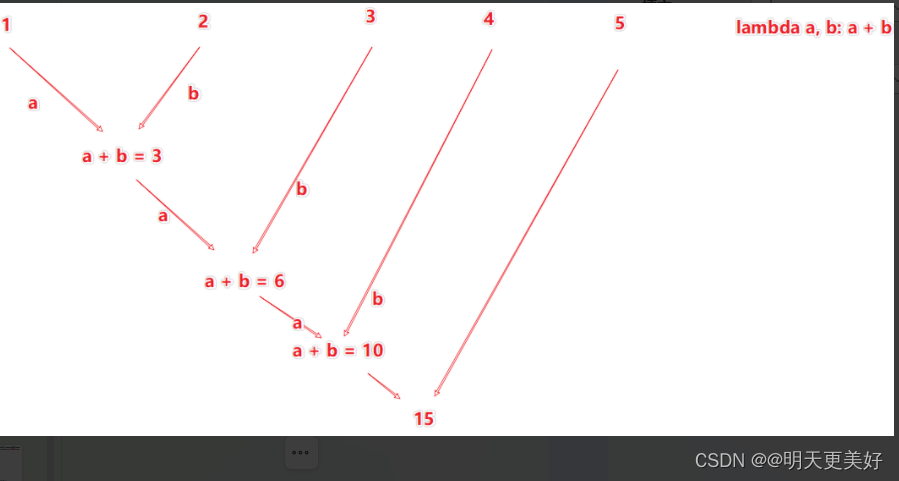
PySpark 数据操作
数据输入 RDD对象 如图可见,PySpark支持多种数据的输入,在输入完成后,都会得到一个:RDD类的对象 RDD全称为:弹性分布式数据集(Resilient Distributed Datasets) PySpark针对数据的处理&…...

FPGA2-采集OV5640乒乓缓存后经USB3.0发送到上位机显示
1.场景 基于特权A7系列开发板,采用OV5640摄像头实时采集图像数据,并将其经过USB3.0传输到上位机显示。这是验证数据流能力的很好的项目。其中,用到的软件版本,如下表所示,基本的硬件情况如下。该项目对应FPGA工程源码…...

亚信科技AntDB数据库专家参加向量数据库首次技术标准研讨会
2023年7月19日下午,中国通信标准化协会大数据技术标准推进委员会数据库与存储工作组(CCSA TC601 WG4)联合中国信通院数据库应用创新实验室(CAICT DBL)在线上召开《向量数据库技术要求》标准首次研讨会。本次会议由中国…...

Windows中实现右键把电子书通过邮件发到kindle
不使用第三方软件,通过Windows自带的函数,可以实现右键将电子书通过电子邮件发送到kindle邮箱,从而实现kindle电子书传送功能。实现过程如下: 1. 使用bat添加右键功能 打开资源管理器,在地址中输入%APPDATA%\Microso…...

Three.js之创建3D场景
参考资料 【G】Three.js官方文档:https://threejs.org/docs/ Three.js是一个流行的WebGL库,官方文档提供了详细的API参考和示例,适合学习和参考。【G】Three.js GitHub链接:https://github.com/mrdoob/three.js 这是一个流行的基…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...