C++ rand的用法
C++ rand的用法
- rand()介绍
- srand()介绍
- 产生随机数的用法
- 产生一定范围随机数的通用表示公式
我们知道 rand() 函数可以用来产生随机数,但是这不是真正意义上的随机数,是一个伪随机数,是根据一个数(我们可以称它为种子)为基准以某个递推公式推算出来的一系列数,当这系列数很大的时候,就符合正态公布,从而相当于产生了随机数,但这不是真正的随机数,当计算机正常开机后,这个种子的值是定了的,除非你破坏了系统。
rand()介绍
- 功能: 随机数发生器
- 用法: int rand(void)
- 所在头文件: stdlib.h
rand() 的内部实现是用线性同余法做的,它不是真的随机数,因其周期特别长,故在一定的范围里可看成是随机的。
rand() 返回一随机数值的范围在 0 至 RAND_MAX 间。RAND_MAX 的范围最少是在 32767 之间(int)。用 unsigned int 双字节是 65535,四字节是 4294967295 的整数范围。0~RAND_MAX 每个数字被选中的机率是相同的。
用户未设定随机数种子时,系统默认的随机数种子为 1。
srand()介绍
rand() 产生的是伪随机数字,每次执行时是相同的; 若要不同, 用函数 srand() 初始化它。
- 功能:初始化随机数发生器
- 用法:void srand(unsigned int seed)
- 所在头文件:stdlib.h
srand() 用来设置 rand() 产生随机数时的随机数种子。参数 seed 必须是个整数,如果每次 seed 都设相同值,rand() 所产生的随机数值每次就会一样。若要不同, 用函数 srand() 初始化它。可以利用 srand((unsigned int)(time(NULL)) 的方法,产生不同的随机数种子,因为每一次运行程序的时间是不同的。
产生随机数的用法
- 给srand()提供一个种子,它是一个unsigned int类型;
- 调用rand(),它会根据提供给srand()的种子值返回一个随机数(在0到RAND_MAX之间);
- 根据需要多次调用rand(),从而不间断地得到新的随机数;
- 无论什么时候,都可以给srand()提供一个新的种子,从而进一步"随机化"rand()的输出结果。
0~RAND_MAX 之间的随机数程序如下:
#include <iostream>
#include <stdlib.h>
#include <time.h> using namespace std; int main()
{ srand((unsigned)time(NULL)); for(int i = 0; i < 10;i++ ) cout << rand() << '/t';cout << endl; return 0;
}
产生一定范围随机数的通用表示公式
- 要取得 [a,b) 的随机整数,使用 (rand() % (b-a))+ a;
- 要取得 [a,b] 的随机整数,使用 (rand() % (b-a+1))+ a;
- 要取得 (a,b] 的随机整数,使用 (rand() % (b-a))+ a + 1;
- 要取得 0~1 之间的浮点数,可以使用rand()/double(RAND_MAX)。
相关文章:

C++ rand的用法
C rand的用法 rand()介绍srand()介绍产生随机数的用法产生一定范围随机数的通用表示公式 我们知道 rand() 函数可以用来产生随机数,但是这不是真正意义上的随机数,是一个伪随机数,是根据一个数(我们可以称它为种子)为基…...
element时间选择器的默认值
概览:vue使用element组件,需要给时间选择器设置默认值,场景一:默认时间选择器,场景二:时间范围选择器,开始时间和结束时间。 一、默认时间选择器 实现思路: element组件的v-model绑…...

fiddler过滤器
1、fiddler Fiddler是一个免费、强大、跨平台的HTTP抓包工具。下载地址 2、为什么适用过滤器 不适用过滤器时,所有的报文都会被抓包。 我们在开发或测试时,只需要抓包某个域名下的报文 ,以“www.baidu.com”为例,不设置过滤器&…...

面试必考精华版Leetcode2130.链表最大孪生和
题目: 代码(首刷看解析 day22): class Solution { public:int pairSum(ListNode* head) {ListNode* slowhead;ListNode* fasthead->next;while(fast->next!nullptr){slowslow->next;fastfast->next->next;}//反转…...

qemu kvm 新建虚拟机
开始菜单打开虚拟机管理器...
Charles抓包工具使用(一)(macOS)
Fiddler抓包 | 竟然有这些骚操作,太神奇了? Fiddler响应拦截数据篡改,实现特殊场景深度测试(一) 利用Fiddler抓包调试工具,实现mock数据特殊场景深度测试(二) 利用Fiddler抓包调试工…...
2023年8月美团外卖3-18元红包优惠券天天领取活动日历及美团外卖红包领取使用
2023年8月美团外卖3-18元红包天天领取活动日历 根据上图美团外卖红包领取活动时间表以下时间可以天天领取3-18元美团外卖红包优惠券: 1、2023年8月18日 可领取美团外卖18元神券节红包; 2、2023年8月每周六、周日每天可领取12元美团外卖节红包ÿ…...

深度学习各层负责什么内容?
1、深度学习——神经网络简介 深度学习(Deep Learning)(也称为深度结构学习【Deep Structured Learning】、层次学习【Hierarchical Learning】或者是深度机器学习【Deep Machine Learning】)是一类算法集合,是机器学习的一个分支。 深度学习方法近年来,…...

【硬件设计】模拟电子基础二--放大电路
模拟电子基础二--放大电路 一、基本放大电路1.1 初始电路1.2 静态工作点1.3 分压偏置电路 二、负反馈放大电路三、直流稳压电路 前言:本章为知识的简单复习,适合于硬件设计学习前的知识回顾,不适合运用于考试。 一、基本放大电路 1.1 初始电…...
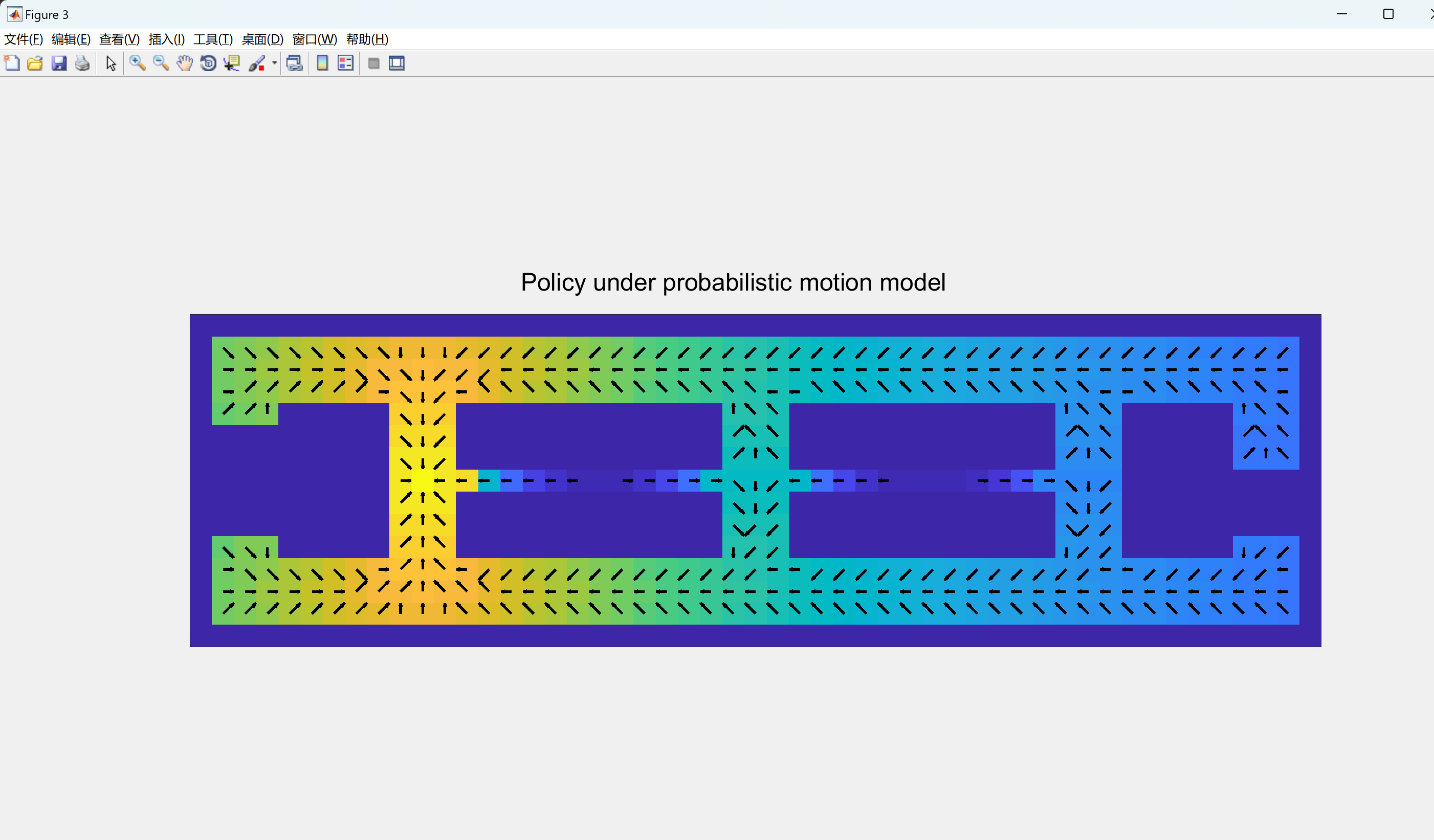
基于应用值迭代的马尔可夫决策过程(MDP)的策略的机器人研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
控件旋转90度,并跟随大小缩放
控件旋转角度,并跟随缩放改变大小 背景使用控件结果 背景 一个项目需求,需要旋转某个控件90使用,在网上找了很多资料,没有特别合适的,自己试水试了一天半,终于弄了个大概其,特此记录 使用控件…...
软件外包开发的PHP开发框架
PHP有许多流行的开发框架,每个框架都有其独特的特点和优势。下面列举的只是一部分PHP开发框架,还有其他一些框架如Slim、Zend Framework等也值得一提。选择合适的框架取决于项目的需求和开发团队的偏好,您可以根据项目规模、复杂性和功能需求…...
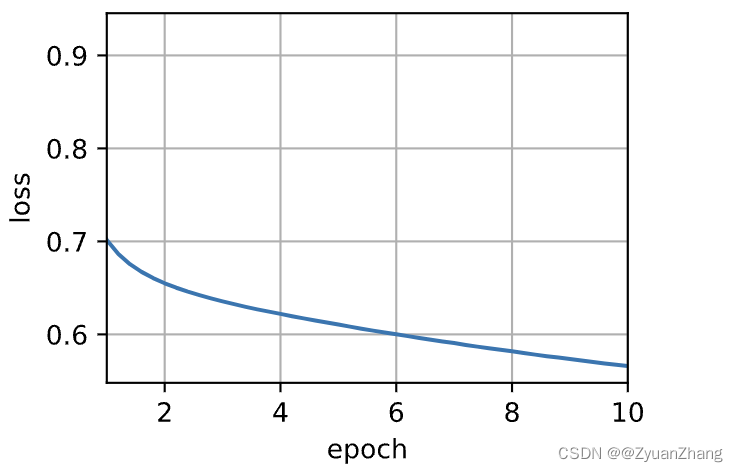
D2L学习记录-10-词嵌入word2vec
NLP-1-词嵌入(word2vec) 参考: 《动手学深度学习 Pytorch 第1版》第10章 自然语言处理 第1、2、3 和 4节 (词嵌入) 词嵌入 (word2vec): 词向量:自然语言中,词是表义的基本单元。词向量是用来表示词的向量。词嵌入 (word embedding)&#x…...

海外独立站怎么搭建?7个海外独立站搭建指南
在海外搭建独立站(独立网站)有几个关键步骤,以下是一个简要的指南: 选择域名和主机: 首先,选择一个适合你网站主题的域名。确保它简洁、易记,并且与你的品牌或内容相关联。 然后,…...

flask中实现restful-api
flask中实现restful-api 举例,我们可以创建一个用于管理任务(Task)的API。在这个例子中,我们将有以下API: GET /tasks: 获取所有任务POST /tasks: 创建一个新的任务GET /tasks/<id>: 获取一个任务的详情PUT /t…...

Centos7 安装man中文版手册
查找man中文安装包: yum search man-pages 安装man-pages-zh-CN.noarch: yum install -y man-pages-zh-CN.noarch...

untiy代码打压缩包,可设置密码
1、简单介绍: 用的是一个插件SharpZipLib,在vs的Nuget下载,也可以去github下载https://github.com/icsharpcode/SharpZipLib 用这个最主要的是因为,这个不用请求windows的文件读写权限,关于这个权限我搞了好久&#…...
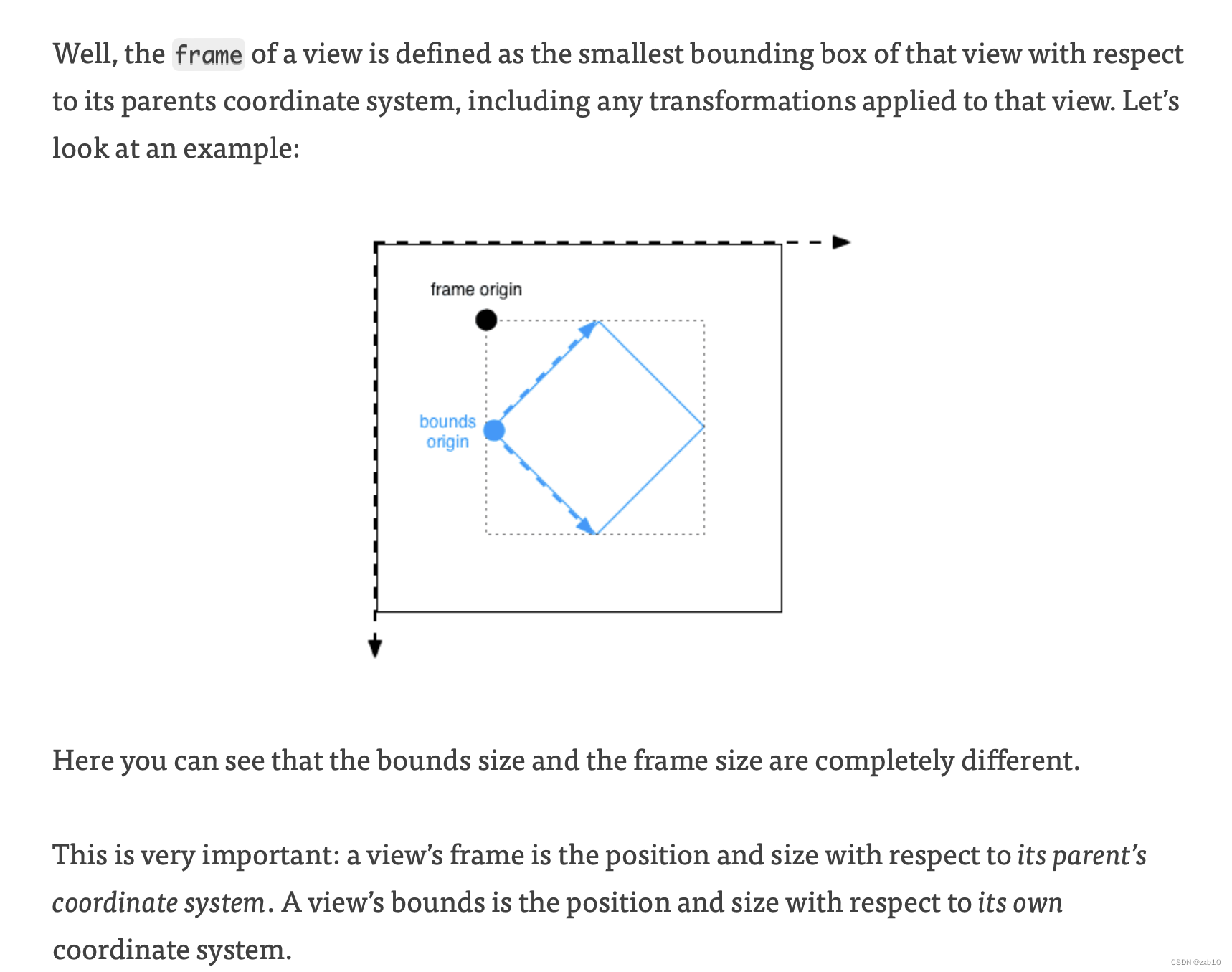
【iOS】—— UIKit相关问题
文章目录 UIKit常用的UIKit组件懒加载的优势 CALayer和UIView区别关系 UITableViewUITableView遵循的两个delegate以及必须实现的方法上述四个必须实现方法执行顺序其他方法的执行顺序: UICollectionView和UITableView的区别UICollectionViewFlowLayout和UICollecti…...

Linux系统防火墙Firewalld
目录 Firewalld概述 Firewalld和iptables的区别 Firewalld网络区域 区域介绍与概念 9个预定义区域 Firewalld数据处理流程 firewalld检查数据包的源地址的规则 Firewalld防火墙的配置方式 常用的firewall-cmd命令选项 服务管理 端口管理 Firewalld概述 Firewalld防火…...
)
STM3232 GPIO的配置寄存器(为了移植IIC)
参考 https://blog.csdn.net/qq_45539458/article/details/129481019 https://blog.csdn.net/weixin_43314829/article/details/125573448?spm1001.2014.3001.5502 https://blog.csdn.net/m0_71548440/article/details/125894236?spm1001.2014.3001.5502 正点原子mini板 stm…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...
