2023.8.2
2022河南萌新联赛第(三)场:河南大学\神奇数字.cpp
//题意:给定三个正整数a b c,求x满足满足abc同余x的个数。
//这个考虑同余的性质,就是两个数的差去取模为0的数肯定是这两个数的同余数,。因此我们计算三个数两两之间差的最大公约数,然后直接分解质因数,计算gcd的因子个数就是x能够用取到的数量。
#include<bits/stdc++.h>#include<iostream>#include<algorithm>#include<map>#include<set>#include<queue>#include<cstring>#include<math.h>#include<map>#include<vector>#include<stack>using namespace std;#define endl '\n'typedef pair<int,int> pr;#define int long long#define ll long long#define fr(i,l,r) for(int i=l;i<=r;i++)#define ufr(i,n,z) for(int i = n;i >= z; i--)#define pb(x) push_back(x)#define all(a) a.begin(),a.end()#define fi first#define se secondconst int N = 1e6+10;const int mod=998244353,inf=LONG_LONG_MAX;int n,m;int a[N];int gcd(int a,int b){return !b?a:gcd(b,a%b);}void solve(){int a,b,c;cin>>a>>b>>c;if(a==b&&a==c){cout<<-1<<'\n';return ;}int x=gcd(abs(a-b),abs(b-c));vector<int>v;for(int i=1;i*i<=x;i++){if(x%i==0){if(i!=x/i)v.push_back(x/i);v.push_back(i);}}sort(v.begin(),v.end());fr(i,0,v.size()-1){cout<<v[i]<<' ';}cout<<'\n';}signed main(){int t=1;cin>>t;while(t--) solve();return 0;}总结://同余的性质 (就是两个数的差去取模为0的数肯定是这两个数的同余数)
//同余式可逐项相加
//同余式可以逐项相乘。
//同余式一边的数可以移到另一边,只要改变符号就可以了
//同余式的每一边都可以增加或减去模的任意倍数。
//同余式两边的数如有公约数,此公约数又和模互素,那么就可以把两边的数除以这个公约数。
//同余式两边的数和模可以同时乘上一个整数。
//同余式两边的数和模可以同时被它们任一公约数除。
//如果同余式对于模m成立,那么它对于m的任意约数相等的模d也成立。
//如果同余式一边上的数和模能被某个数除尽,则同余式的另一边的数也能被这个数除尽。
//同余式一边上的数与模的最大公约数,等于另一边上的数与模的最大公约数
2022河南萌新联赛第(三)场:河南大学\逆序对计数.cpp
//题意:给定长度为n的排列(0<=n<=6000),每次询问为如果将l,r翻转,则逆序对的个数
//思路: 对于一个排列, 如果区间反转, 逆序数等于区间中所有的对数减去当前的逆序对数, 即原本的正序对变为逆序对, 原本的逆序对变为正序对。
//改变区间在整个区间的位置不重要,逆序对的增减只会在区间进行
/* #include<bits/stdc++.h>#include<iostream>#include<algorithm>#include<map>#include<set>#include<queue>#include<cstring>#include<math.h>#include<map>#include<vector>#include<stack>using namespace std;#define endl '\n'typedef pair<int,int> pr;#define int long long#define ll long long#define fr(i,l,r) for(int i=l;i<=r;i++)#define ufr(i,n,z) for(int i = n;i >= z; i--)#define pb(x) push_back(x)#define all(a) a.begin(),a.end()#define fi first#define se secondconst int N = 1e6+10;const int mod=998244353,inf=LONG_LONG_MAX;int n,m;int a[N];int s[6010][6010];int change(int l,int r){int len=r-l+1;int x=len*(len-1)/2;return x-2*s[l][r];}void solve(){cin>>n;fr(i,1,n){cin>>a[i];}int res=0;fr(i,1,n){ //预处理所有l,r的逆序数个数fr(j,1,i){s[j][i]=s[j][i-1];}int cnt=0;ufr(j,i-1,1){if(a[j]>a[i]){cnt++;res++;}s[j][i]+=cnt;}}cin>>m;while(m--){int l,r;cin>>l>>r;cout<<res+change(l,r)<<'\n';}}signed main(){int t=1;// cin>>t;while(t--) solve();return 0;} *///树状数组做法#include<bits/stdc++.h>#include<iostream>#include<algorithm>#include<map>#include<set>#include<queue>#include<cstring>#include<math.h>#include<map>#include<vector>#include<stack>using namespace std;#define endl '\n'typedef pair<int,int> pr;#define int long long#define ll long long#define fr(i,l,r) for(int i=l;i<=r;i++)#define ufr(i,n,z) for(int i = n;i >= z; i--)#define pb(x) push_back(x)#define all(a) a.begin(),a.end()#define fi first#define se secondconst int N = 1e6+10;const int mod=998244353,inf=LONG_LONG_MAX;int n,m;int a[N];int t[N];int f[6010][6010];void add(int x){for(int i=x;i<=n;i+=i&-i){t[i]+=1;}}int query(int x){int ans=0;for(int i=x;i;i-=i&-i){ans+=t[i];}return ans;}void solve(){cin>>n;fr(i,1,n){cin>>a[i];}fr(i,1,n){fr(j,i,n){f[i][j]=f[i][j-1]+(j-i-query(a[j])); //(j-i-query(a[j])即区间-正序对个数add(a[j]);}fr(j,1,n){t[j]=0;}}cin>>m;int res=f[1][n];while(m--){int l,r;cin>>l>>r;cout<<res+(r-l+1)*(r-l)/2-2*f[l][r]<<'\n';}}signed main(){int t=1;// cin>>t;while(t--) solve();return 0;}P1045 [NOIP2003 普及组] 麦森数(高精度快速幂)
题意:输入P(1000<=p<=3100000),输出2^p-1的位数及最后500位数
#include<iostream>
#include<math.h>
#include<cstring>
using namespace std;
int f[1001], p, res[1001], sav[1001];//乘法要开两倍长度
void result_1() {memset(sav, 0, sizeof(sav));for (register int i = 1; i <= 500; i += 1)for (register int j = 1; j <= 500; j += 1)sav[i + j - 1] += res[i] * f[j];//先计算每一位上的值(不进位)for (register int i = 1; i <= 500; i += 1){sav[i + 1] += sav[i] / 10;//单独处理进位问题,不容易出错sav[i] %= 10;}memcpy(res, sav, sizeof(res));//cstring库里的赋值函数,把sav的值赋给res
}
void result_2() {memset(sav, 0, sizeof(sav));for (register int i = 1; i <= 500; i += 1)for (register int j = 1; j <= 500; j += 1)sav[i + j - 1] += f[i] * f[j];for (register int i = 1; i <= 500; i += 1){sav[i + 1] += sav[i] / 10;sav[i] %= 10;}memcpy(f, sav, sizeof(f));
}
int main() {cin >> p;cout << int(log10(2) * p + 1) << '\n'; //2^p-1,2^p的位数res[1] = 1;f[1] = 2;while (p) {if (p % 2 == 1) {result_1();}result_2();p >>= 1;}res[1] -= 1;for ( int i = 500; i >= 1; i--)//注意输出格式,50个换一行,第一个不用if (i != 500 && i % 50 == 0)printf("\n%d", res[i]);else printf("%d", res[i]);return 0;
}数位dp
(最高位限制,记忆化搜索,枚举位的大小,前导0)
洛谷P2657 [SCOI2009] windy 数
windy定义了一种windy数。不含前导零且相邻两个数字之差至少为2的正整数被称为windy数。
windy想知道,在A和B之间,包括A和B,总共有多少个windy数?
#include<iostream>
#include<cstring>
using namespace std;
int num[12], dp[12][12];
int dfs(int pos, int pre, int limit, int lead) {int ans = 0, i, up;if (pos == -1) //搜完return 1; //用作计数if (!limit && dp[pos][pre] != -1 && !lead)//没有最高位限制,已经搜过了,并且没有前导0return dp[pos][pre]; //记忆化搜索up = limit ? num[pos] : 9;//当前位最大数字 for (i = 0; i <= up; i++) {//从0枚举到最大数字 if (lead) {//有前导0不受限制 ans += dfs(pos - 1, i, limit && i == up, lead && i == 0);}else if (i - pre >= 2 || i - pre <= -2)//无前导0受限 ans += dfs(pos - 1, i, limit && i == up, lead && i == 0);}if (!limit && !lead)//没有最高位限制且没有前导0时记录结果 dp[pos][pre] = ans;return ans;
}
int solve(int x) {int pos = 0;while (x) {num[pos++] = x % 10;x /= 10;} //按位储存return dfs(pos - 1, -1, 1, 1);
}
int main() {ios::sync_with_stdio(false);int lt, rt;cin >> lt >> rt;memset(dp, -1, sizeof(dp));cout<< solve(rt) - solve(lt - 1)<<'\n';return 0;
}相关文章:

2023.8.2
2022河南萌新联赛第(三)场:河南大学\神奇数字.cpp //题意:给定三个正整数a b c,求x满足满足abc同余x的个数。 //这个考虑同余的性质,就是两个数的差去取模为0的数肯定是这两个数的同余数,。因此我们计算三个数两两之…...

windows运行窗口常用快捷键命令
winr打开运行窗口,然后输入快捷命令:(当然utools和win11搜索也挺好用的) cmd : 命令行窗口(命令提示符窗口、cmd窗口)regedit : 注册表mspaint : 画图工具services.msc : 本地服务设置(比如查看mysql服务是否启动成功)devmgmt.ms…...
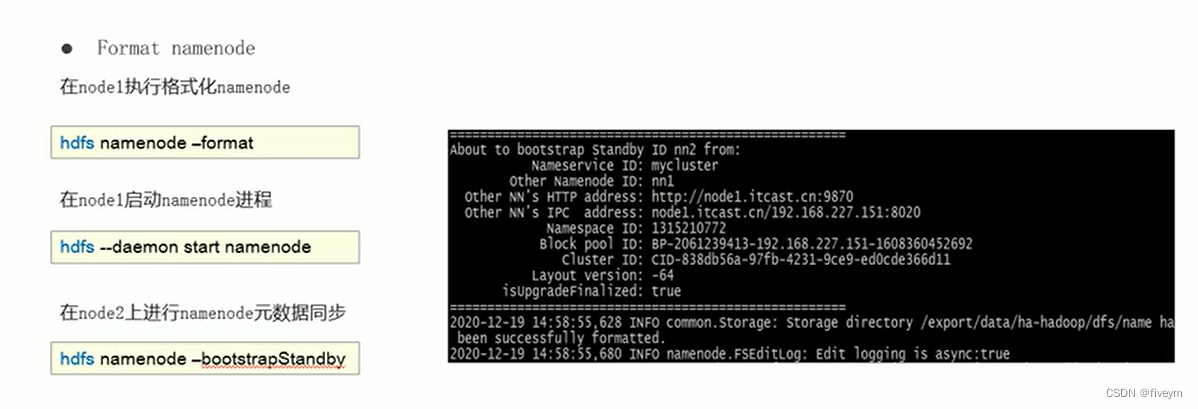
HDFS的QJM方案
Quorum Journal Manager仲裁日志管理器 介绍主备切换,脑裂问题解决---ZKFailoverController(zkfc)主备切换,脑裂问题解决-- Fencing(隔离)机制主备数据状态同步问题解决 HA集群搭建集群基础环境准备HA集群规…...
安装win版本的neo4j(2023最新版本)
安装win版本的neo4j 写在最前面安装 win版本的neo4j1. 安装JDK2.下载配置环境变量(也可选择直接点击快捷方式,就可以不用配环境了)3. 启动neo4j 测试代码遇到的问题及解决(每次环境都太离谱了,各种问题)连接…...

ChatGPT结合知识图谱构建医疗问答应用 (二) - 构建问答流程
一、ChatGPT结合知识图谱 上篇文章对医疗数据集进行了整理,并写入了知识图谱中,本篇文章将结合 ChatGPT 构建基于知识图谱的问答应用。 下面是上篇文章的地址: ChatGPT结合知识图谱构建医疗问答应用 (一) - 构建知识图谱 这里实现问答的流程…...

聊天系统登录后端实现
定义返回的数据格式 # Restful API from flask import jsonifyclass HttpCode(object):# 响应正常ok 200# 没有登陆错误unloginerror 401# 没有权限错误permissionerror 403# 客户端参数错误paramserror 400# 服务器错误servererror 500def _restful_result(code, messa…...
)
Ajax笔记_01(知识点、包含代码和详细解析)
Ajax_01笔记 前置知识点 在JavaScript中 问题1:将数组转为字符串,以及字符串转为数组的方式。 问题2、将对象转为字符串,以及字符串转为对象的方法。 方法: 问题1: 将数组转为字符串可以使用 join() 方法。例如&…...

Eureka 学习笔记2:EurekaClient
版本 awsVersion ‘1.11.277’ EurekaClient 接口实现了 LookupService 接口,拥有唯一的实现类 DiscoveryClient 类。 LookupService 接口提供以下功能: 获取注册表根据应用名称获取应用根据实例 id 获取实例信息 public interface LookupService<…...

Spring引入并启用log4j日志框架-----Spring框架
<?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/POM/4.0.0 http://ma…...

Redis实现延时队列
缓存队列延时向接口报工,并支持多实例部署。 引入依赖 <dependency><groupId>org.redisson</groupId><artifactId>redisson-spring-data</artifactId><version>3.17.4</version> </dependency> 注入RedisClient …...

无限遍历,Python实现在多维嵌套字典、列表、元组的JSON中获取数据
目录 背景 思路 新建两个函数A和B,函数 A处理字典数据,被调用后,判断传递的参数,如果参数为字典,则调用自身; 如果是列表或者元组,则调用列表处理函数B; 函数 B处理列表&#x…...

信息学奥赛一本通——1180:分数线划定
文章目录 题目【题目描述】【输入】【输出】【输入样例】【输出样例】【提示】 AC代码 题目 【题目描述】 世博会志愿者的选拔工作正在 A 市如火如荼的进行。为了选拔最合适的人才,A市对所有报名的选手进行了笔试,笔试分数达到面试分数线的选手方可进入…...

SpringApplication对象的构建及spring.factories的加载时机
构建SpringApplication对象源码: 1、调用启动类的main()方法,该方法中调用SpringApplication的run方法。 SpringBootApplication public class SpringbootdemoApplication {public static void main(String[] args) {SpringApplication.run(SpringbootdemoApplication.class, …...

基于传统检测算法hog+svm实现图像多分类
直接上效果图: 代码仓库和视频演示b站视频005期: 到此一游7758258的个人空间-到此一游7758258个人主页-哔哩哔哩视频 代码展示: 数据集在datasets文件夹下 运行01train.py即可训练 训练结束后会保存模型在本地 运行02pyqt.py会有一个可视化…...
 方法,使用 concat() 方法, [...originalArray],find(filter),移出类名 removeAttr())
slice() 方法,使用 concat() 方法, [...originalArray],find(filter),移出类名 removeAttr()
在JavaScript中,在 JavaScript 中,clone 不是一个原生的数组方法。但是你可以使用其他方法来实现克隆数组的功能。 以下是几种常见的克隆数组的方法: 使用 slice() 方法: const originalArray [1, 2, 3]; const clonedArray …...

Zabbix报警机制、配置钉钉机器人、自动发现、主动监控概述、配置主动监控、zabbix拓扑图、nginx监控实例
day02 day02配置告警用户数超过50,发送告警邮件实施验证告警配置配置钉钉机器人告警创建钉钉机器人编写脚本并测试添加报警媒介类型为用户添加报警媒介创建触发器创建动作验证自动发现配置自动发现主动监控配置web2使用主动监控修改配置文件,只使用主动…...
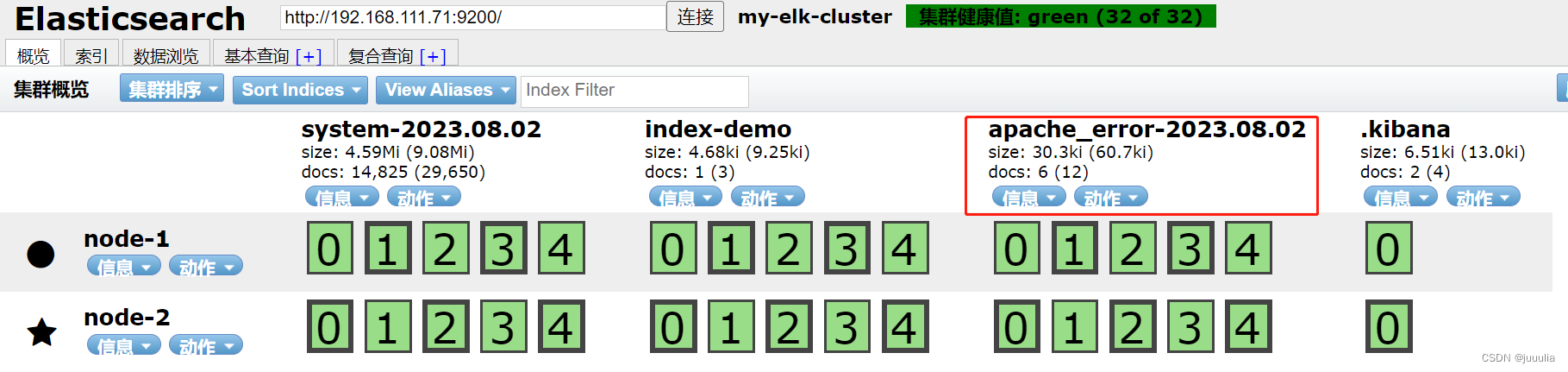
ELK日志分析系统概述及部署
ELK 平台是一套完整的日志集中处理解决方案,将 ElasticSearch、Logstash 和 Kibana 三个开源工具配合使用,完成更强大的用户对日志的查询、排序、统计需求。 一、ELK概述 1、组件说明 ①ElasticSearch ElasticSearch是基于Lucene(一个全文…...

HTML拖拽
拖拽的流程:鼠标按下(mousedown)→鼠标移动(mousemove)→鼠标松开(moveup) 需要理解的几个api: clientX/clientY: 相对于浏览器视窗内的位置坐标(不包括浏览器收藏夹和顶部网址部分)pageX/pageY: 该属性会考虑滚动,如…...
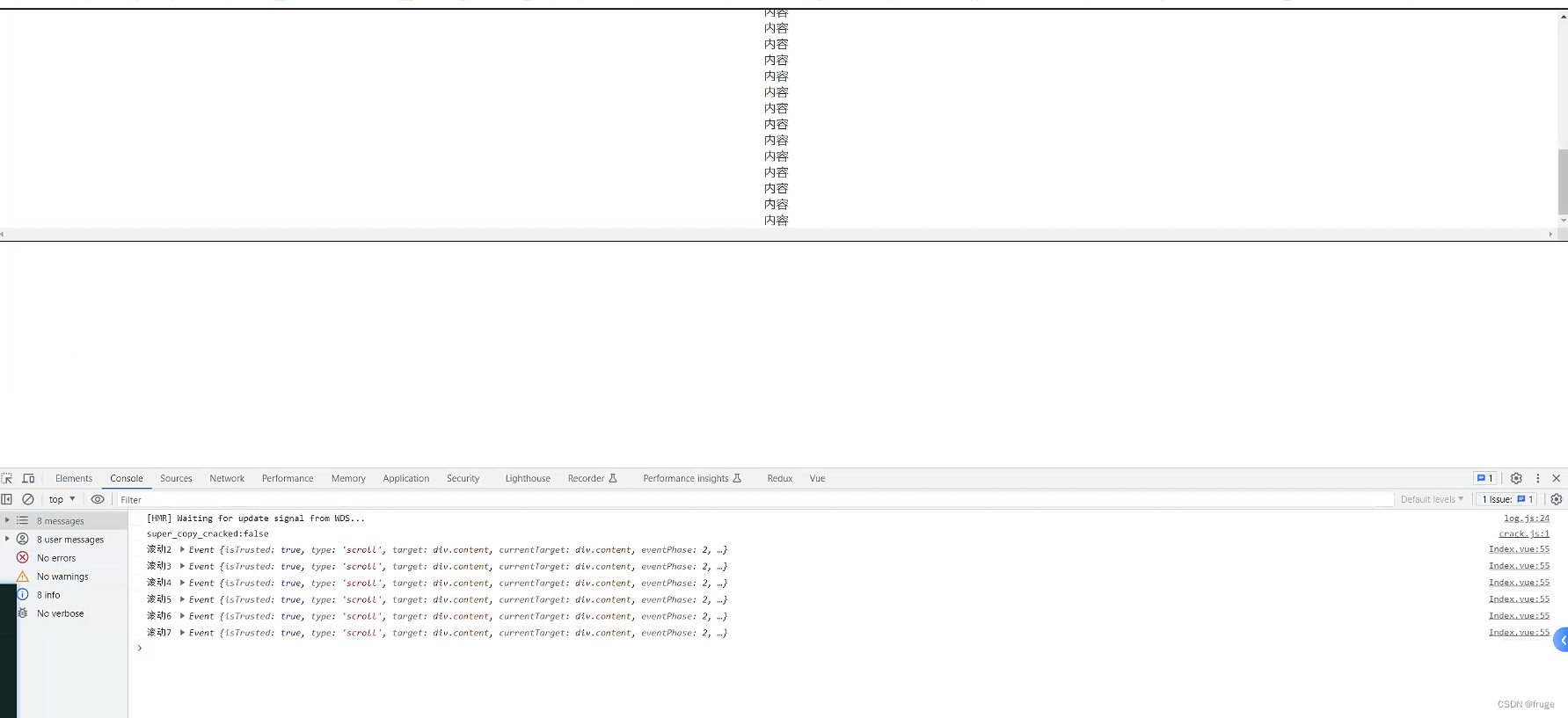
【vue】 vue2 监听滚动条滚动事件
代码 直接上代码,vue单文件 index.vue <template><div class"content" scroll"onScroll"><p>内容</p><p>内容</p><p>内容</p><p>内容</p><p>内容</p><p>内容…...

k8s目录
k8s笔记目录,更新中... 一 概念篇 1.1概念介绍 1.2 pod 1.3 controller 1.3.1 deployment 1.3.2 statefulset 1.3.3 daemonset 1.3.4 job和cronJob1 1.4 serivce和ingress 1.5 配置与存储 1.5.1 configMap 1.5.2 secret 1.5.3 持久化存储 1.5.4 pv和…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...
