【基础理论】了解点过程

一、说明
在这个世界上,会发生许多事件,其趋势可能遵循一种模式。在这篇博客中,我们试图为这些模式建模奠定基础。例如,在已经发生地震的地区,新地震的可能性通常会增加。这种可能性的增加主要是因为早期地震造成的余震。在一个国家/地区恐慌性抛售股票可能会导致另一个国家/地区发生类似事件。
以野火为例,今年亚马逊森林的野火可以大大减少来年另一场野火的发生。明年发生野火的可能性下降主要是因为现有森林燃料的燃烧。因此,很明显,类似事件的概率可以通过先前事件序列中的模式来增加或降低。
如果类似事件的概率提高,即每次发生都会增加未来发生的速率,就像地震的例子一样,那么这些事件可以归类为随机兴奋或自激发。如果类似事件的概率降低,如地震示例,那么这些事件可以归类为随机抑制或自我调节。如果类似事件的概率不受影响,则每次发生对未来发生的速率没有任何影响,则这些事件可以建模为泊松点过程
二、点过程理论
点过程是时间和/或空间中事件发生的随机模型。在这篇博客中,我们将强调点过程的纯时间方面,即点落下的空间只是代表时间的实线的一部分。
2.1 计数过程( N(t) )
首先,考虑一条表示时间和事件时间 T₁、T₂ 的线,...在沿直线下降的事件时间中,T i(事件时间)通常可以解释为第i 个事件的发生时间。此事件可以是特定地区的地震或亚马逊森林的野火。我们的工作是对这些事件时间进行建模。而不是对这些事件时间进行建模 T₁、T₂ ,...Tn,也可以用计数过程N(t)来描述。
计数过程 N(t) 可以看作是截至当前时间 t 之前进入系统的“到达”数量的累积计数。如果自安装地震仪以来的146年里,喜马拉雅山发生了80次地震,那么N(80)=146次。足够简单吧!
让我们也定义历史:H(u)到达时间u的历史。
2.2 条件强度函数 ( λ٭(t) )
当我们讨论随机性的概念时,定义一个函数是相关的,该函数给出事件在时间 t 发生的期望。该函数称为强度函数,表示为 λ٭(t),它表示事件预期在特定时间 t 附近发生的无穷小速率。 它以时间 t 之前点过程的先验历史 H(t) 为条件。

我们引入了诸如“自激发”和“自我调节”之类的术语,这些术语可以使用条件强度函数轻松理解。如果最近到达历史H(t)导致条件强度函数增加,则该过程称为自激发。一般来说,λ٭(t) 不仅取决于 t,还取决于前面事件的 Ti 倍数,即 H(t)。
当N为泊松点过程时,条件强度函数λ٭(t)仅取决于当前时间的信息,而不依赖于历史H(u)。泊松点过程既不是自激的,也不是自调节的。
λ٭(t) 只是泊松点过程随时间变化的函数,平稳泊松过程具有恒定的条件速率:λ٭(t) = α,对于所有 t。 λ٭(t) = α 意味着在任何时间点,事件发生的概率都是恒定的,无论此类事件发生的频率如何。
三、霍克斯Hawkes过程
霍克斯过程属于一个以它的创造者Alan G. Hawkes命名的自激点过程家族。自激励点过程模型是使用时间聚类的模型事件。像“地震”和“恐慌性抛售股票”这样的事件通常是在时间上聚集的,即事件的到来增加了在不久的将来观察到此类事件的可能性。让我们定义霍克斯条件强度函数 —
定义 {t1, t2, . . . , tk} 表示截至时间 t 的点过程过去到达时间的观测序列,霍克斯条件强度为

常数λ称为背景强度,μ(·)称为激发函数。如果μ(·)等于零,则此自激点过程简化为简单的平稳泊松过程。激励函数的常见选择μ(·)是指数衰减。
![]()
参数α和β是常量。α,β可以解释为系统中的每次到达都会立即将到达强度增加α,然后随着时间的推移,这种到达的影响以β的速度衰减。

修改后的霍克斯条件强度如下所示。幂律函数中另一个常用的激励函数。
α 和 β 是 λ٭(t) 的参数,设 θ 表示参数。点过程的参数向量 θ 是通过最大化对数似然函数来估计的。我们还可以使用参数函数来近似条件强度函数,我们将在本博客系列的下一篇博客中对此进行更多讨论。
自激点过程有一个明显的延伸,即互激点过程。这些本质上是一组一维点过程,它们激发自己和彼此。这组点过程称为多变量或相互激励的点过程。
如果对于每个 i = 1, . . . , m,则每个计数过程 Ni(t) 具有以下形式的条件强度:

四、模拟
让我们模拟一个简单的霍克斯点过程:λ:0.1,α:0.1,β:0.1,并尝试理解条件强度函数。

我们可以清楚地观察到上图中的激发和衰减。现在让我们将背景强度 λ 增加到 0.5。
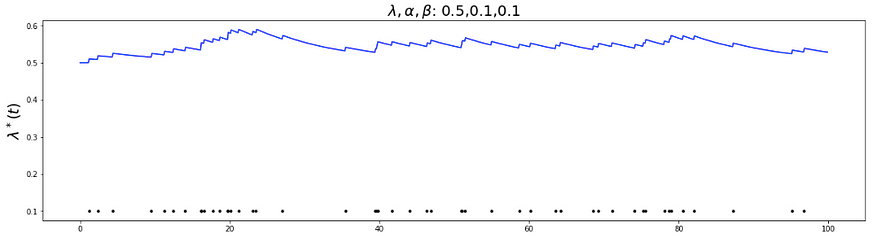
我们清楚地看到,随着背景强度的增加并徘徊在0.5以上,事件的数量也在增加。我们现在将尝试了解α的影响,β。让我们将α增加到 0.5。

我们可以清楚地看到,事件的数量增加了,这是因为事件的每一次发生都会使下一个事件的到达强度增加α。因此,λ٭(t)的增加变得更高,一个有趣的观察结果是λ٭(t)从0.1到0.6变化。
现在让我们将β增加到 0.5。请记住β控制事件的衰减率对其连续事件的影响。
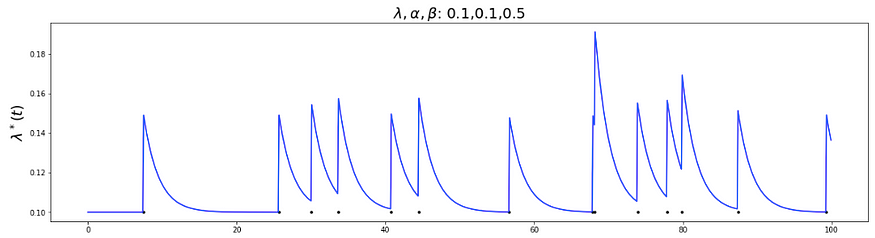
将此图与图1进行比较,图1中的衰减非常小于图4中的衰减。
霍克斯点过程的核心概念在上面的例子中得到了演示。
点工艺在各个领域都有广泛的应用。我们可以在连续的时间内对离散事件/事件的流进行建模。我们还可以使用函数近似,其中多个事件类型的条件强度函数可以通过像 LSTM 这样的新型神经架构来近似。在本系列的下一篇博客中,我们将讨论神经霍克斯过程。
相关文章:

【基础理论】了解点过程
Maximum tsunami wave height generated by the 16 Sept. 2015 Chile earthquake, from the International Tsunami Information Center. Posted by Austin Elliott 一、说明 在这个世界上,会发生许多事件,其趋势可能遵循一种模式。在这篇博客中&#…...

深入理解Spring MVC中的@ResponseBody注解
引言 在现代的Web应用开发中,数据的传递和交互是不可或缺的一部分。Spring MVC作为一个强大的框架,在处理客户端请求和响应时,提供了许多注解来简化开发过程。其中,ResponseBody注解在处理方法的返回值时起到了关键作用࿰…...
大数据学习教程:Linux高级教程(下)
四、大数据集群服务器搭建 1. 新增Linux服务器 1.1、克隆虚拟机 学习环境中,一般使用VMware虚拟机克隆Linux系统,用来进行集群服务器的搭建。 VMware支持两种类型的克隆:完整克隆、链接克隆 完整克隆是和原始虚拟机完全独立的一个复制&…...

1.Oracle建表及使用
1.概述 1. 表:用于 存储数据 -- 是我们最常见的数据库对象 2. 表设计注意事项 (1) 表设计时,尽量遵从 第三范式(3NF) (2) 名称不能超过 30 个字符 -- 超过会报错 (3) 名称只能以 字母 大头,可由数字、 _、 $…...
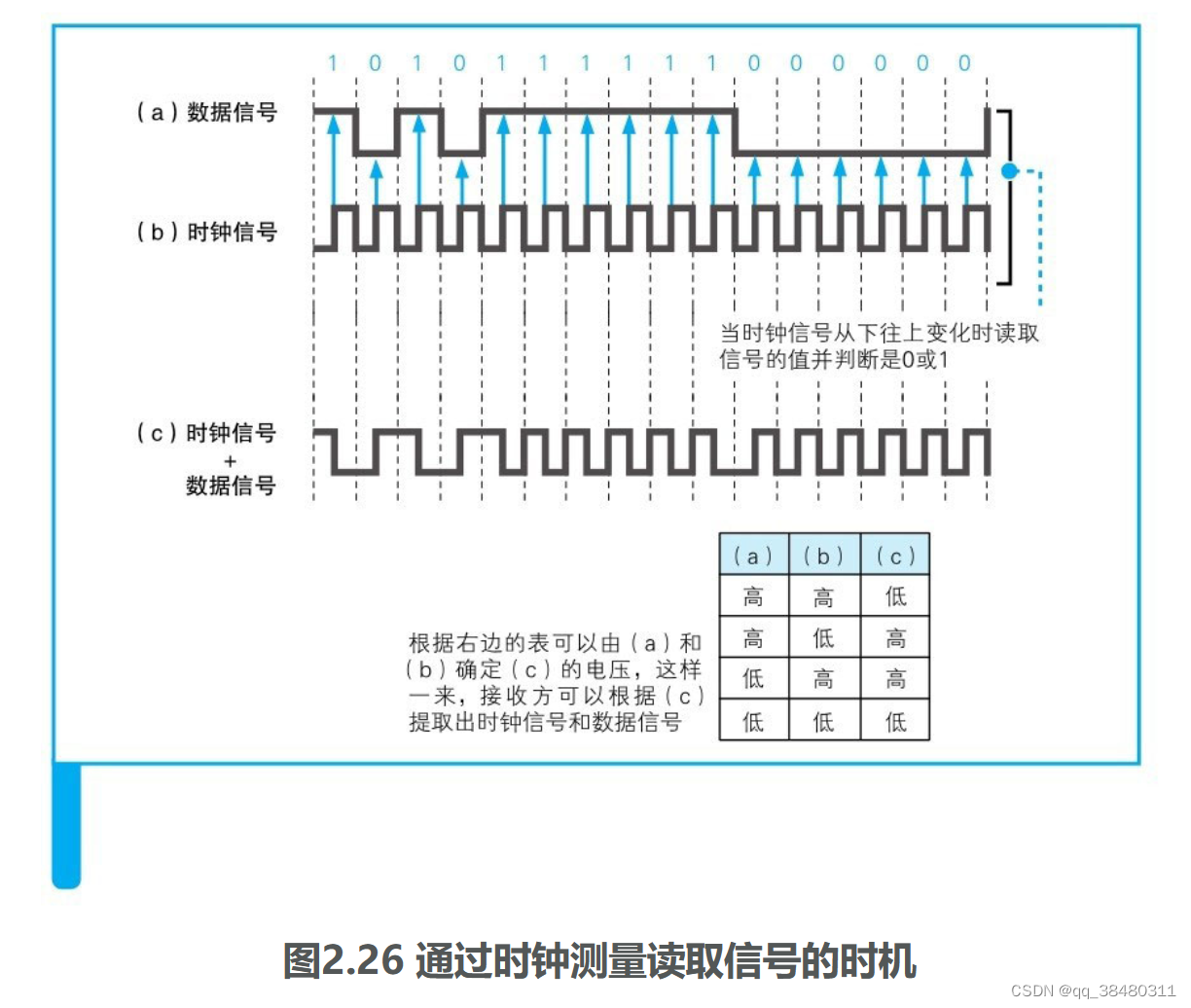
《网络是怎样连接的》(二.2)
(6条消息) 《网络是怎样连接的》(二.1)_qq_38480311的博客-CSDN博客 本文主要取材于 《网络是怎样连接的》 第二章 2.5 2.6章节。 目录 简述: 本文的主要内容是 以太网的收发操作 和 UDP协议的收发操作。 IP与以太网的包收发操作 包是什…...

MySQL加密插件安装
加密插件 查看已经安装的插件:show plugs; 增加加密插件: 登陆MySQL后,通过show variables like ‘validate%’;查看相关验证规则。 ① 在配置文件中新增,[mysqld]标签下 plugin-load-addvalidate_password.so ② 在运行时新增…...

新手入门Jenkins自动化部署入门详细教程
1. 背景 在实际开发中,我们经常要一边开发一边测试,当然这里说的测试并不是程序员对自己代码的单元测试,而是同组程序员将代码提交后,由测试人员测试; 或者前后端分离后,经常会修改接口,然后重新…...
Neural Network学习笔记4
完整的模型训练套路 train.py import torch import torchvision from torch.utils.data import DataLoader # 引入自定义的网络模型 from torch.utils.tensorboard import SummaryWriterfrom model import *# 准备数据集 train_data torchvision.datasets.CIFAR10(root"…...

[转]关于cmake --build .的理解
https://blog.csdn.net/qq_38563206/article/details/126486183 https://blog.csdn.net/HandsomeHong/article/details/120170219 cmake --build . 该命令的含义是:执行当前目录下的构建系统,生成构建目标。 cmake项目构建过程简述: 1. 首先…...
【Linux下6818开发板(ARM)】硬件空间挂载
(꒪ꇴ꒪ ),hello我是祐言博客主页:C语言基础,Linux基础,软件配置领域博主🌍快上🚘,一起学习!送给读者的一句鸡汤🤔:集中起来的意志可以击穿顽石!作者水平很有限,如果发现错误&#x…...

剑指offer 动态规划篇
题目由入门往上递增 入门 斐波那契数列_牛客题霸_牛客网 (nowcoder.com) 动态规划甚至于算法的入门题目 方法一:按照斐波那契的公式fnfn-1fn-2,从1-n求出结果。 class Solution { public:int Fibonacci(int n) {vector<int>f{0,1,1};for(int …...
自动化部署的一些笔记)
关于Linux中前端负载均衡之VIP(LVS+Keepalived)自动化部署的一些笔记
写在前面 整理一些 LVS 相关的笔记理解不足小伙伴帮忙指正 傍晚时分,你坐在屋檐下,看着天慢慢地黑下去,心里寂寞而凄凉,感到自己的生命被剥夺了。当时我是个年轻人,但我害怕这样生活下去,衰老下去。在我看来…...

C++ 拷贝交换技术示例
拷贝交换技术(copy and swap)是什么,网上估计能查到很多。但网上有点难找到完整的演示代码,所以这里记录一下。难点在于: 如果要满足 5 的原则,我到底要写那些函数? 默认构造函数、复制构造函数…...
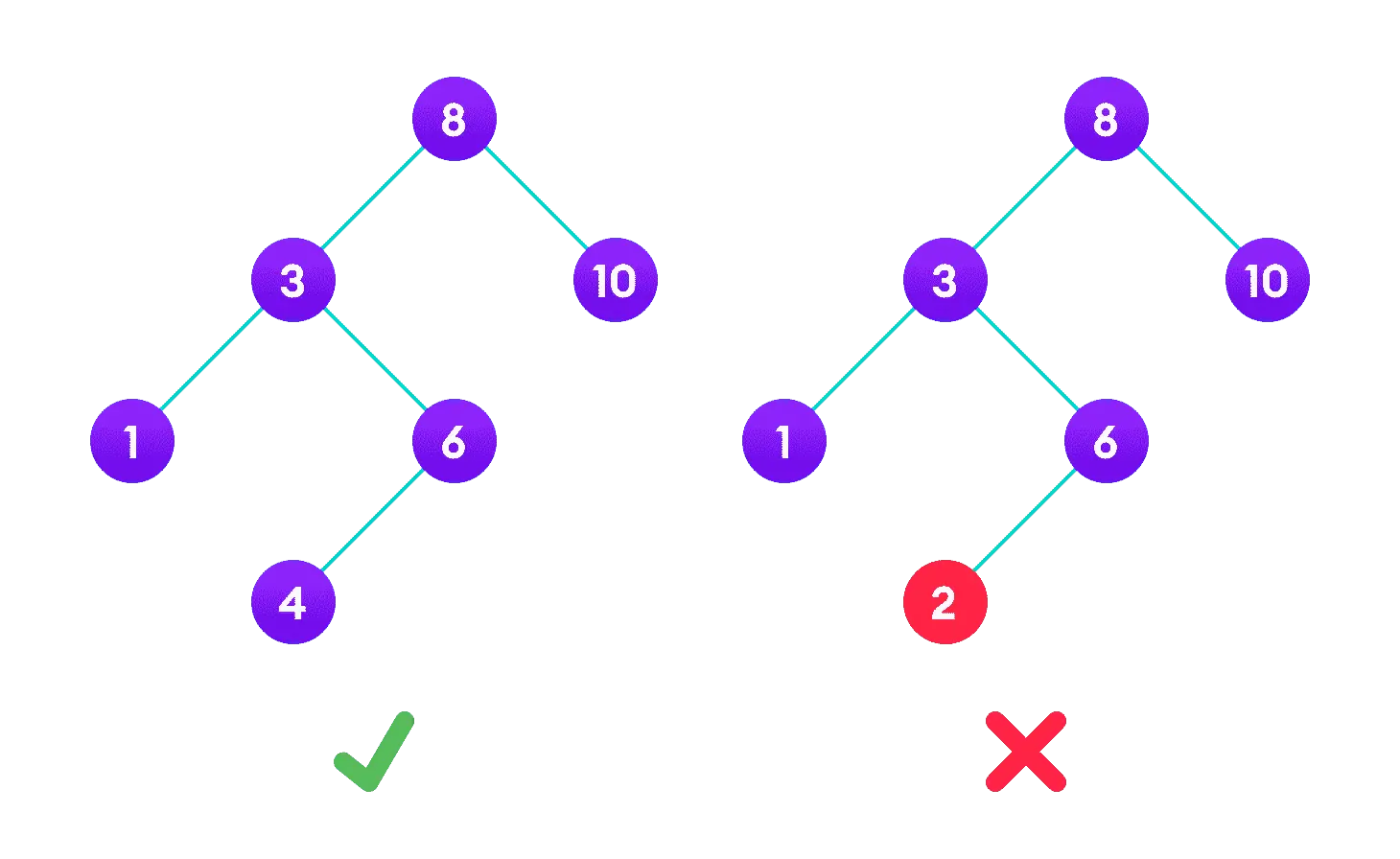
使用 Go 语言实现二叉搜索树
原文链接: 使用 Go 语言实现二叉搜索树 二叉树是一种常见并且非常重要的数据结构,在很多项目中都能看到二叉树的身影。 它有很多变种,比如红黑树,常被用作 std::map 和 std::set 的底层实现;B 树和 B 树,…...

系统接口自动化测试方案
XXX接口自动化测试方案 1、引言 1.1 文档版本 版本 作者 审批 备注 V1.0 XXXX 创建测试方案文档 1.2 项目情况 项目名称 XXX 项目版本 V1.0 项目经理 XX 测试人员 XXXXX,XXX 所属部门 XX 备注 1.3 文档目的 本文档主要用于指导XXX-Y…...
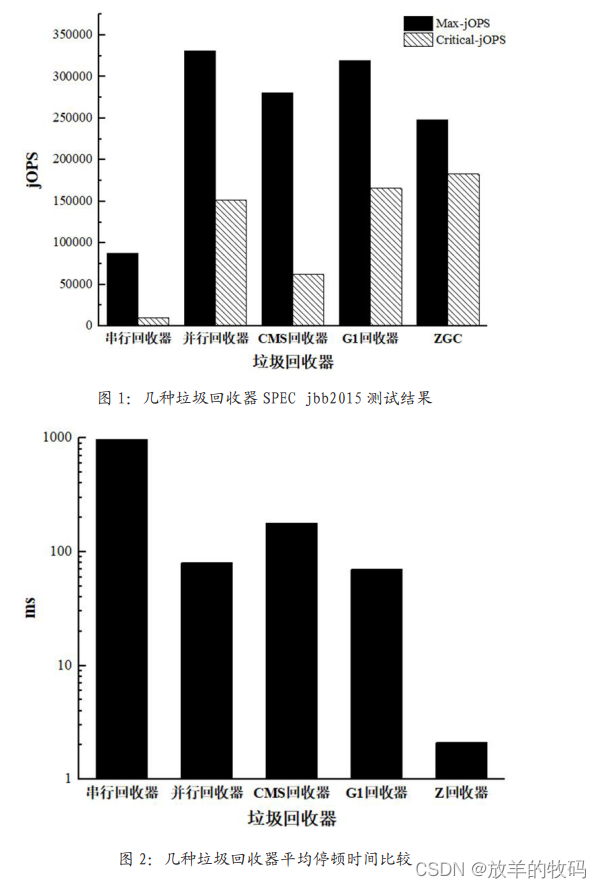
小研究 - JVM 垃圾回收方式性能研究(一)
本文从几种JVM垃圾回收方式及原理出发,研究了在 SPEC jbb2015基准测试中不同垃圾回收方式对于JVM 性能的影响,并通过最终测试数据对比,给出了不同应用场景下如何选择垃圾回收策略的方法。 目录 1 引言 2 垃圾回收算法 2.1 标记清除法 2.2…...
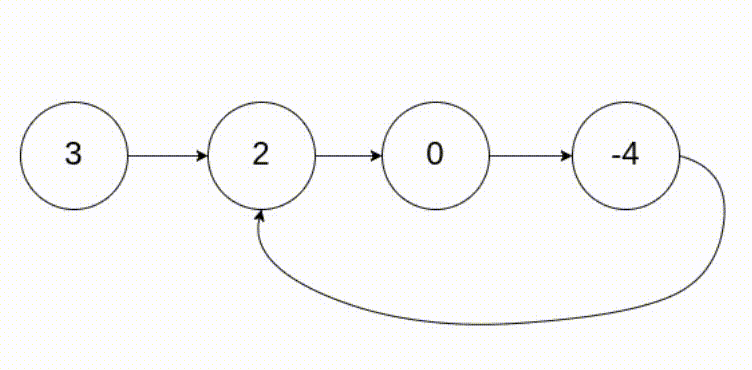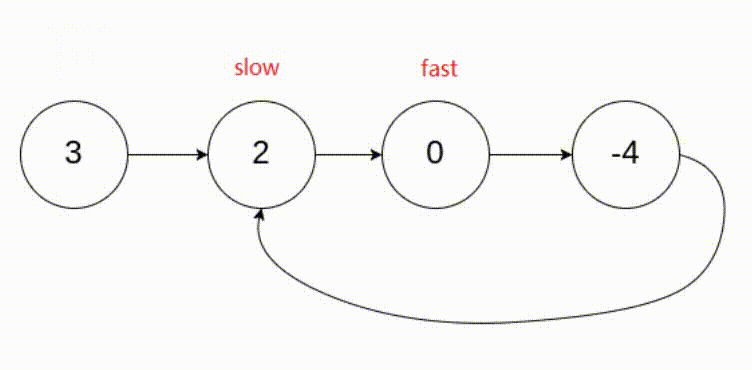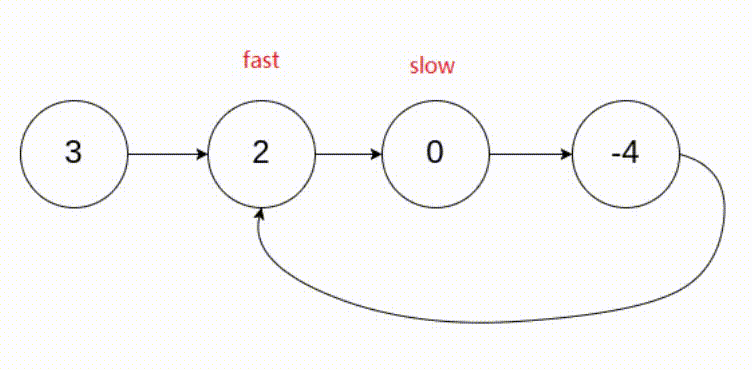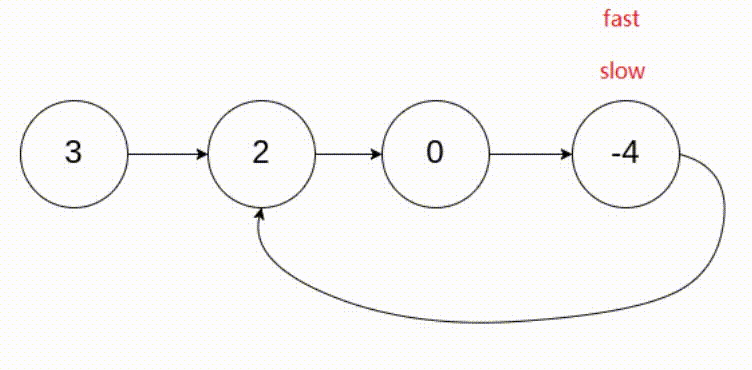
[LeetCode]链表相关题目(c语言实现)
文章目录 LeetCode203. 移除链表元素LeetCode237. 删除链表中的节点LeetCode206. 反转链表ⅠLeetCode92. 反转链表 II思路 1思路 2 LeetCode876. 链表的中间结点剑指 Offer 22. 链表中倒数第k个节点LeetCode21. 合并两个有序链表LeetCode86. 分隔链表LeetCode234. 回文链表Leet…...
] NAND 初始化常用命令:复位 (Reset) 和 Read ID 和 Read UID 操作和代码实现)
[深入理解NAND Flash (操作篇)] NAND 初始化常用命令:复位 (Reset) 和 Read ID 和 Read UID 操作和代码实现
依JEDEC eMMC及经验辛苦整理,原创保护,禁止转载。 专栏 《深入理解Flash:闪存特性与实践》 内容摘要 全文 4400 字,主要内容 复位的目的和作用? NAND Reset 种类:FFh, FCh, FAh, FDh 区别 Reset 操作步骤 和 代码实现 Read ID 操作步骤 和 代码实现 Read Uni…...

RxJava 复刻简版之二,调用流程分析之案例实现
接上篇:https://blog.csdn.net/da_ma_dai/article/details/131878516 代码节点:https://gitee.com/bobidali/lite-rx-java/commit/05199792ce75a80147c822336b46837f09229e46 java 类型转换 kt 类型: Any Object泛型: 协变: …...

SpringMVC中Model和ModelAndView的区别
SpringMVC中Model和ModelAndView的区别 两者的区别: 在SpringMVC中,Model和ModelAndView都是用于将数据传递到视图层的对象 Model是”模型“的意思,是MVC架构中的”M“部分,是用来传输数据的。 理解成MVC架构中的”M“和”V“…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

DeepSeek越强,Kimi越慌?
被DeepSeek吊打的Kimi,还有多少人在用? 去年,月之暗面创始人杨植麟别提有多风光了。90后清华学霸,国产大模型六小虎之一,手握十几亿美金的融资。旗下的AI助手Kimi烧钱如流水,单月光是投流就花费2个亿。 疯…...
:电商转化率优化与网站性能的底层逻辑)
精益数据分析(98/126):电商转化率优化与网站性能的底层逻辑
精益数据分析(98/126):电商转化率优化与网站性能的底层逻辑 在电子商务领域,转化率与网站性能是决定商业成败的核心指标。今天,我们将深入解析不同类型电商平台的转化率基准,探讨页面加载速度对用户行为的…...

使用 uv 工具快速部署并管理 vLLM 推理环境
uv:现代 Python 项目管理的高效助手 uv:Rust 驱动的 Python 包管理新时代 在部署大语言模型(LLM)推理服务时,vLLM 是一个备受关注的方案,具备高吞吐、低延迟和对 OpenAI API 的良好兼容性。为了提高部署效…...

Python[数据结构及算法 --- 栈]
一.栈的概念 在 Python 中,栈(Stack)是一种 “ 后进先出(LIFO)”的数据结构,仅允许在栈顶进行插入(push)和删除(pop)操作。 二.栈的抽象数据类型 1.抽象数…...
-Hive数据分析)
大数据学习(129)-Hive数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言📝支持一…...
