使用 Go 语言实现二叉搜索树
原文链接: 使用 Go 语言实现二叉搜索树
二叉树是一种常见并且非常重要的数据结构,在很多项目中都能看到二叉树的身影。
它有很多变种,比如红黑树,常被用作 std::map 和 std::set 的底层实现;B 树和 B+ 树,广泛应用于数据库系统中。
本文要介绍的二叉搜索树用的也很多,比如在开源项目 go-zero 中,就被用来做路由管理。
这篇文章也算是一篇前导文章,介绍一些必备知识,下一篇再来介绍具体在 go-zero 中的应用。
二叉搜索树的特点
最重要的就是它的有序性,在二叉搜索树中,每个节点的值都大于其左子树中的所有节点的值,并且小于其右子树中的所有节点的值。
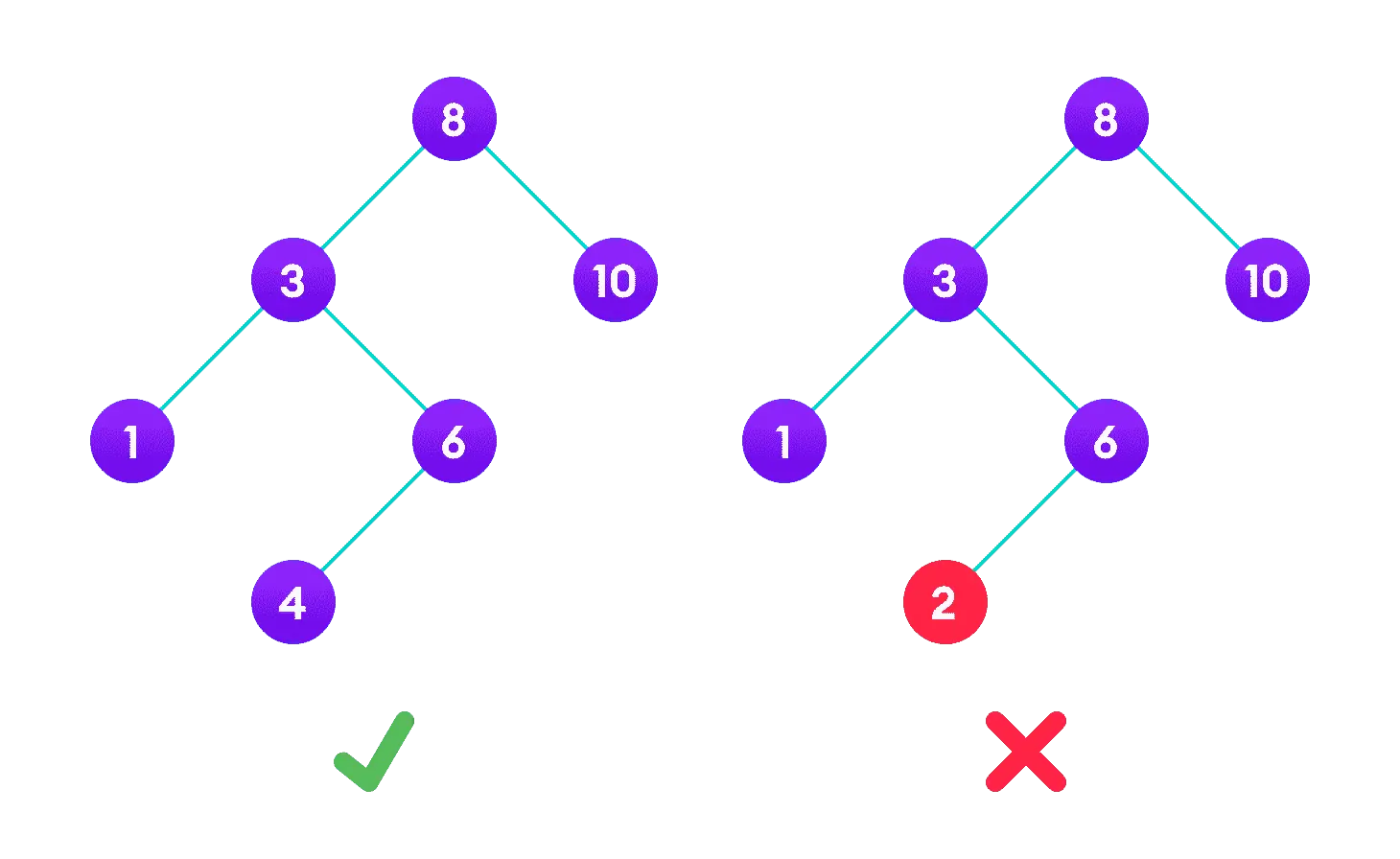
这意味着通过二叉搜索树可以快速实现对数据的查找和插入。
Go 语言实现
本文主要实现了以下几种方法:
Insert(t):插入一个节点Search(t):判断节点是否在树中InOrderTraverse():中序遍历PreOrderTraverse():前序遍历PostOrderTraverse():后序遍历Min():返回最小值Max():返回最大值Remove(t):删除一个节点String():打印一个树形结构
下面分别来介绍,首先定义一个节点:
type Node struct {key intvalue Itemleft *Node //leftright *Node //right
}
定义树的结构体,其中包含了锁,是线程安全的:
type ItemBinarySearchTree struct {root *Nodelock sync.RWMutex
}
插入操作:
func (bst *ItemBinarySearchTree) Insert(key int, value Item) {bst.lock.Lock()defer bst.lock.Unlock()n := &Node{key, value, nil, nil}if bst.root == nil {bst.root = n} else {insertNode(bst.root, n)}
}// internal function to find the correct place for a node in a tree
func insertNode(node, newNode *Node) {if newNode.key < node.key {if node.left == nil {node.left = newNode} else {insertNode(node.left, newNode)}} else {if node.right == nil {node.right = newNode} else {insertNode(node.right, newNode)}}
}
在插入时,需要判断插入节点和当前节点的大小关系,保证搜索树的有序性。
中序遍历:
func (bst *ItemBinarySearchTree) InOrderTraverse(f func(Item)) {bst.lock.RLock()defer bst.lock.RUnlock()inOrderTraverse(bst.root, f)
}// internal recursive function to traverse in order
func inOrderTraverse(n *Node, f func(Item)) {if n != nil {inOrderTraverse(n.left, f)f(n.value)inOrderTraverse(n.right, f)}
}
前序遍历:
func (bst *ItemBinarySearchTree) PreOrderTraverse(f func(Item)) {bst.lock.Lock()defer bst.lock.Unlock()preOrderTraverse(bst.root, f)
}// internal recursive function to traverse pre order
func preOrderTraverse(n *Node, f func(Item)) {if n != nil {f(n.value)preOrderTraverse(n.left, f)preOrderTraverse(n.right, f)}
}
后序遍历:
func (bst *ItemBinarySearchTree) PostOrderTraverse(f func(Item)) {bst.lock.Lock()defer bst.lock.Unlock()postOrderTraverse(bst.root, f)
}// internal recursive function to traverse post order
func postOrderTraverse(n *Node, f func(Item)) {if n != nil {postOrderTraverse(n.left, f)postOrderTraverse(n.right, f)f(n.value)}
}
返回最小值:
func (bst *ItemBinarySearchTree) Min() *Item {bst.lock.RLock()defer bst.lock.RUnlock()n := bst.rootif n == nil {return nil}for {if n.left == nil {return &n.value}n = n.left}
}
由于树的有序性,想要得到最小值,一直向左查找就可以了。
返回最大值:
func (bst *ItemBinarySearchTree) Max() *Item {bst.lock.RLock()defer bst.lock.RUnlock()n := bst.rootif n == nil {return nil}for {if n.right == nil {return &n.value}n = n.right}
}
查找节点是否存在:
func (bst *ItemBinarySearchTree) Search(key int) bool {bst.lock.RLock()defer bst.lock.RUnlock()return search(bst.root, key)
}// internal recursive function to search an item in the tree
func search(n *Node, key int) bool {if n == nil {return false}if key < n.key {return search(n.left, key)}if key > n.key {return search(n.right, key)}return true
}
删除节点:
func (bst *ItemBinarySearchTree) Remove(key int) {bst.lock.Lock()defer bst.lock.Unlock()remove(bst.root, key)
}// internal recursive function to remove an item
func remove(node *Node, key int) *Node {if node == nil {return nil}if key < node.key {node.left = remove(node.left, key)return node}if key > node.key {node.right = remove(node.right, key)return node}// key == node.keyif node.left == nil && node.right == nil {node = nilreturn nil}if node.left == nil {node = node.rightreturn node}if node.right == nil {node = node.leftreturn node}leftmostrightside := node.rightfor {//find smallest value on the right sideif leftmostrightside != nil && leftmostrightside.left != nil {leftmostrightside = leftmostrightside.left} else {break}}node.key, node.value = leftmostrightside.key, leftmostrightside.valuenode.right = remove(node.right, node.key)return node
}
删除操作会复杂一些,分三种情况来考虑:
- 如果要删除的节点没有子节点,只需要直接将父节点中,指向要删除的节点指针置为
nil即可 - 如果删除的节点只有一个子节点,只需要更新父节点中,指向要删除节点的指针,让它指向删除节点的子节点即可
- 如果删除的节点有两个子节点,我们需要找到这个节点右子树中的最小节点,把它替换到要删除的节点上。然后再删除这个最小节点,因为最小节点肯定没有左子节点,所以可以应用第二种情况删除这个最小节点即可
最后是一个打印树形结构的方法,在实际项目中其实并没有实际作用:
func (bst *ItemBinarySearchTree) String() {bst.lock.Lock()defer bst.lock.Unlock()fmt.Println("------------------------------------------------")stringify(bst.root, 0)fmt.Println("------------------------------------------------")
}// internal recursive function to print a tree
func stringify(n *Node, level int) {if n != nil {format := ""for i := 0; i < level; i++ {format += " "}format += "---[ "level++stringify(n.left, level)fmt.Printf(format+"%d\n", n.key)stringify(n.right, level)}
}
单元测试
下面是一段测试代码:
func fillTree(bst *ItemBinarySearchTree) {bst.Insert(8, "8")bst.Insert(4, "4")bst.Insert(10, "10")bst.Insert(2, "2")bst.Insert(6, "6")bst.Insert(1, "1")bst.Insert(3, "3")bst.Insert(5, "5")bst.Insert(7, "7")bst.Insert(9, "9")
}func TestInsert(t *testing.T) {fillTree(&bst)bst.String()bst.Insert(11, "11")bst.String()
}// isSameSlice returns true if the 2 slices are identical
func isSameSlice(a, b []string) bool {if a == nil && b == nil {return true}if a == nil || b == nil {return false}if len(a) != len(b) {return false}for i := range a {if a[i] != b[i] {return false}}return true
}func TestInOrderTraverse(t *testing.T) {var result []stringbst.InOrderTraverse(func(i Item) {result = append(result, fmt.Sprintf("%s", i))})if !isSameSlice(result, []string{"1", "2", "3", "4", "5", "6", "7", "8", "9", "10", "11"}) {t.Errorf("Traversal order incorrect, got %v", result)}
}func TestPreOrderTraverse(t *testing.T) {var result []stringbst.PreOrderTraverse(func(i Item) {result = append(result, fmt.Sprintf("%s", i))})if !isSameSlice(result, []string{"8", "4", "2", "1", "3", "6", "5", "7", "10", "9", "11"}) {t.Errorf("Traversal order incorrect, got %v instead of %v", result, []string{"8", "4", "2", "1", "3", "6", "5", "7", "10", "9", "11"})}
}func TestPostOrderTraverse(t *testing.T) {var result []stringbst.PostOrderTraverse(func(i Item) {result = append(result, fmt.Sprintf("%s", i))})if !isSameSlice(result, []string{"1", "3", "2", "5", "7", "6", "4", "9", "11", "10", "8"}) {t.Errorf("Traversal order incorrect, got %v instead of %v", result, []string{"1", "3", "2", "5", "7", "6", "4", "9", "11", "10", "8"})}
}func TestMin(t *testing.T) {if fmt.Sprintf("%s", *bst.Min()) != "1" {t.Errorf("min should be 1")}
}func TestMax(t *testing.T) {if fmt.Sprintf("%s", *bst.Max()) != "11" {t.Errorf("max should be 11")}
}func TestSearch(t *testing.T) {if !bst.Search(1) || !bst.Search(8) || !bst.Search(11) {t.Errorf("search not working")}
}func TestRemove(t *testing.T) {bst.Remove(1)if fmt.Sprintf("%s", *bst.Min()) != "2" {t.Errorf("min should be 2")}
}
上文中的全部源码都是经过测试的,可以直接运行,并且已经上传到了 GitHub,需要的同学可以自取。
以上就是本文的全部内容,如果觉得还不错的话欢迎点赞,转发和关注,感谢支持。
源码地址:
- https://github.com/yongxinz/go-example
推荐阅读:
- Go 语言 select 都能做什么?
- Go 语言 context 都能做什么?
参考文章:
- https://flaviocopes.com/golang-data-structure-binary-search-tree/
相关文章:

使用 Go 语言实现二叉搜索树
原文链接: 使用 Go 语言实现二叉搜索树 二叉树是一种常见并且非常重要的数据结构,在很多项目中都能看到二叉树的身影。 它有很多变种,比如红黑树,常被用作 std::map 和 std::set 的底层实现;B 树和 B 树,…...

系统接口自动化测试方案
XXX接口自动化测试方案 1、引言 1.1 文档版本 版本 作者 审批 备注 V1.0 XXXX 创建测试方案文档 1.2 项目情况 项目名称 XXX 项目版本 V1.0 项目经理 XX 测试人员 XXXXX,XXX 所属部门 XX 备注 1.3 文档目的 本文档主要用于指导XXX-Y…...
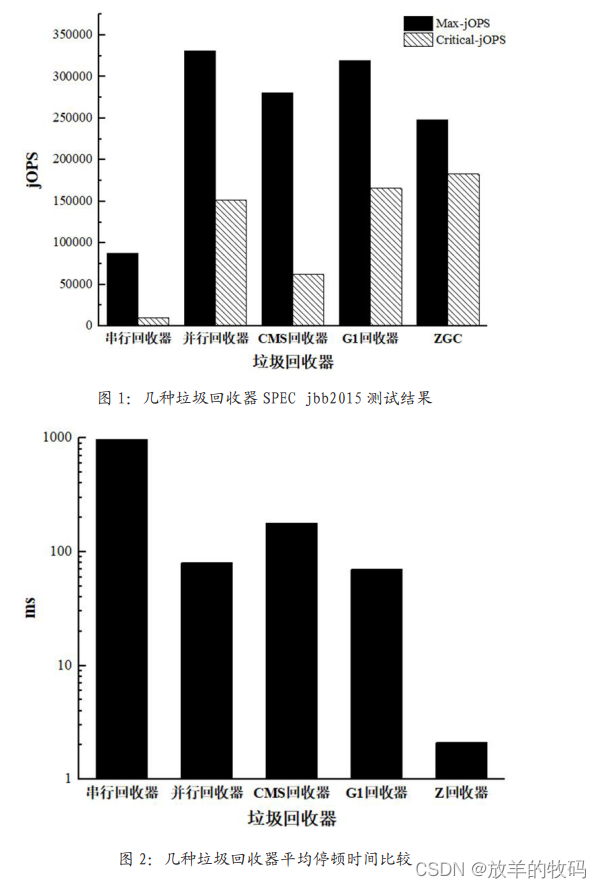
小研究 - JVM 垃圾回收方式性能研究(一)
本文从几种JVM垃圾回收方式及原理出发,研究了在 SPEC jbb2015基准测试中不同垃圾回收方式对于JVM 性能的影响,并通过最终测试数据对比,给出了不同应用场景下如何选择垃圾回收策略的方法。 目录 1 引言 2 垃圾回收算法 2.1 标记清除法 2.2…...
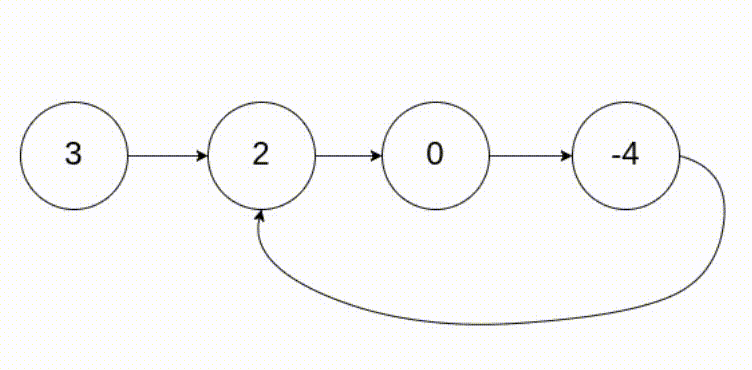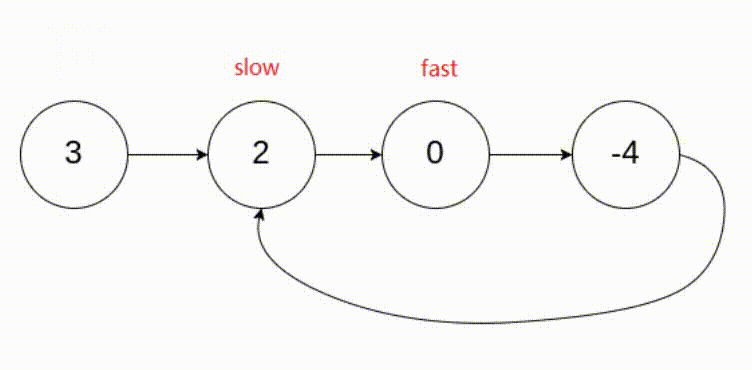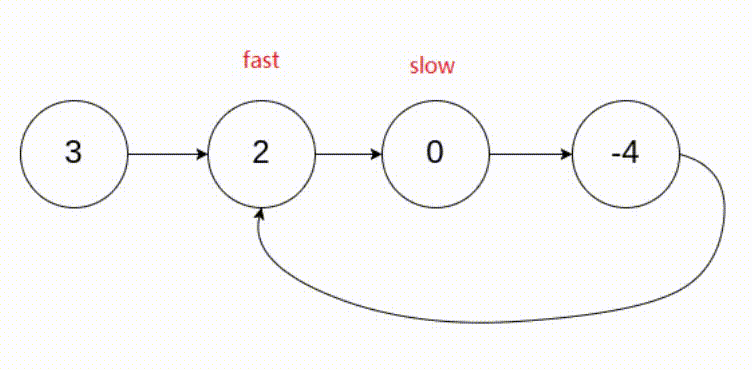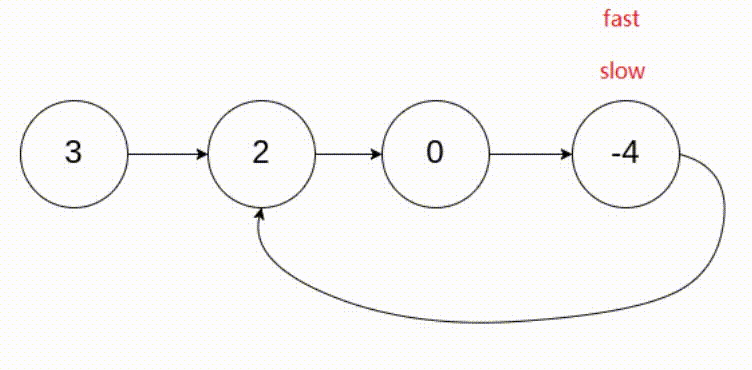
[LeetCode]链表相关题目(c语言实现)
文章目录 LeetCode203. 移除链表元素LeetCode237. 删除链表中的节点LeetCode206. 反转链表ⅠLeetCode92. 反转链表 II思路 1思路 2 LeetCode876. 链表的中间结点剑指 Offer 22. 链表中倒数第k个节点LeetCode21. 合并两个有序链表LeetCode86. 分隔链表LeetCode234. 回文链表Leet…...
] NAND 初始化常用命令:复位 (Reset) 和 Read ID 和 Read UID 操作和代码实现)
[深入理解NAND Flash (操作篇)] NAND 初始化常用命令:复位 (Reset) 和 Read ID 和 Read UID 操作和代码实现
依JEDEC eMMC及经验辛苦整理,原创保护,禁止转载。 专栏 《深入理解Flash:闪存特性与实践》 内容摘要 全文 4400 字,主要内容 复位的目的和作用? NAND Reset 种类:FFh, FCh, FAh, FDh 区别 Reset 操作步骤 和 代码实现 Read ID 操作步骤 和 代码实现 Read Uni…...

RxJava 复刻简版之二,调用流程分析之案例实现
接上篇:https://blog.csdn.net/da_ma_dai/article/details/131878516 代码节点:https://gitee.com/bobidali/lite-rx-java/commit/05199792ce75a80147c822336b46837f09229e46 java 类型转换 kt 类型: Any Object泛型: 协变: …...

SpringMVC中Model和ModelAndView的区别
SpringMVC中Model和ModelAndView的区别 两者的区别: 在SpringMVC中,Model和ModelAndView都是用于将数据传递到视图层的对象 Model是”模型“的意思,是MVC架构中的”M“部分,是用来传输数据的。 理解成MVC架构中的”M“和”V“…...
Tomcat安装与管理
文章目录 Tomcat安装及管理Tomcat gz包安装:JDK安装:Tomcat安装:修改配置文件(如下):服务启动配置: Tomcat-管理(部署jpress):修改允许访问的主机修改允许管理APP的主机进入管理&…...

React之路由
React之路由 背景: react: 18.2.0 路由:react-router-dom: 6.14.2 1、路由表配置 src下新建router/index.ts import React, { lazy } from react import { Navigate } from react-router-dom import Layout from /layout/Index import { JSX } from rea…...
机器学习深度学习——非NVIDIA显卡怎么做深度学习(坑点排查)
👨🎓作者简介:一位即将上大四,正专攻机器学习的保研er 🌌上期文章:机器学习&&深度学习——数值稳定性和模型化参数(详细数学推导) 📚订阅专栏:机器…...

2021 Robocom 决赛 第四题
原题链接: PTA | 程序设计类实验辅助教学平台 题面: 在一个名叫刀塔的国家里,有一只猛犸正在到处跑着,希望能够用它的长角抛物技能来撞飞别人。已知刀塔国有 N 座城市,城市之间由 M 条道路互相连接,为了拦…...
线程池-手写线程池Linux C简单版本(生产者-消费者模型)
目录 简介手写线程池线程池结构体分析task_ttask_queue_tthread_pool_t 线程池函数分析thread_pool_createthread_pool_postthread_workerthread_pool_destroywait_all_donethread_pool_free 主函数调用 运行结果 简介 本线程池采用C语言实现 线程池的场景: 当某些…...

05-向量的意义_n维欧式空间
线性代数 什么是向量?究竟为什么引入向量? 为什么线性代数这么重要?从研究一个数拓展到研究一组数 一组数的基本表示方法——向量(Vector) 向量是线性代数研究的基本元素 e.g. 一个数: 666,…...

交通运输安全大数据分析解决方案
当前运输市场竞争激烈,道路运输企业受传统经营观念影响,企业管理者安全意识淡薄,从业人员规范化、流程化的管理水平较低,导致制度规范在落实过程中未能有效监督与管理,执行过程中出现较严重的偏差,其营运车…...
)
vimrc 配置 (持续跟新中)
vimrc 配置 #显示行号 set nu #自动换行 set autoindent #设置tab键 宽度为四个空格 set tabstop4 set shiftwidth4 set expandtab更多文章,详见我的博客网站...

【集成学习介绍】
1. 引言 在机器学习领域,集成学习(Ensemble Learning)是一种强大的技术,通过将多个弱学习器组合成一个更强大的集成模型,来提升模型的鲁棒性和性能。 2. 集成学习的原理 集成学习的核心思想是“三个臭皮匠ÿ…...

动画制作选择Blender还是Maya
Blender和Maya是两种最广泛使用的 3D 建模和动画应用程序。许多经验丰富的用户表示,Blender 在雕刻工具方面远远领先于 Maya,并且在 3D 建模方面达到了相同的质量水平。对于刚接触动画行业的人来说,您可能会问“我应该使用 Blender 还是 Maya…...
215. 数组中的第K个最大元素
题目链接:力扣 解题思路: 方法一:基于快速排序 因为题目中只需要找到第k大的元素,而快速排序中,每一趟排序都可以确定一个最终元素的位置。 当使用快速排序对数组进行降序排序时,那么如果有一趟排序过程…...

NLP From Scratch: 生成名称与字符级RNN
NLP From Scratch: 生成名称与字符级RNN 这是我们关于“NLP From Scratch”的三个教程中的第二个。 在<cite>第一个教程< / intermediate / char_rnn_classification_tutorial ></cite> 中,我们使用了 RNN 将名称分类为来源语言。 这次ÿ…...

Spring MVC程序开发
目录 1.什么是Spring MVC? 1.1MVC定义 1.2MVC和Spring MVC的关系 2.为什么要学习Spring MVC? 3.怎么学Spring MVC? 3.1Spring MVC的创建和连接 3.1.1创建Spring MVC项目 3.1.2RequestMapping 注解介绍 3.1.3 RequestMapping 是 post 还是 get 请求? …...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...

TJCTF 2025
还以为是天津的。这个比较容易,虽然绕了点弯,可还是把CP AK了,不过我会的别人也会,还是没啥名次。记录一下吧。 Crypto bacon-bits with open(flag.txt) as f: flag f.read().strip() with open(text.txt) as t: text t.read…...
