C++ 拷贝交换技术示例
拷贝交换技术(copy and swap)是什么,网上估计能查到很多。但网上有点难找到完整的演示代码,所以这里记录一下。难点在于:
- 如果要满足 5 的原则,我到底要写那些函数?
默认构造函数、复制构造函数、析构函数、swap函数。剩下三个函数是固定模板(boilerplate),不用写与类相关的代码。由于两种重载赋值运算符合并成一个了,所以只剩两个函数需要写固定模板。 - 哪些是
noexcept的?
必须是noexcept的函数:移动构造函数,重载赋值运算符(注意只剩一个了),交换函数。 - 交换函数和
std::swap的关系如何?
必须自己写一个属于这个类的交换函数,在实现拷贝交换技术时不能调用std::swap。在类外面,可以通过using std::swap;的方法,让编译器优先选用自己实现swap函数,如不存在,再回退到std::swap;在类外面也可以直接都用std::swap,无所谓。
#include <cassert> // assert
#include <utility> // swapclass Demo {using Self = Demo;public:int ichi{}; // Note 1: 这里初始化为 0,又在默认构造函数初始化为 1,是为了说明委托默认构造函数的作用。特别地,如果存在成员没有用大括号初始化,就更需要委托默认构造函数完成所有成员的初始化。// 要么为 nullptr,要么为大小为 1 的数组。int* ein{};public:// Note 2: 默认构造函数是否是 constexpr, noexcept 的,视实际情况而定。constexpr Demo() noexcept : ichi{ 1 }, ein{ nullptr } {}// Note 3: 复制构造函数通常涉及内存分配,一般不是 noexcept 的。Demo(const Self& other) : Demo() { // Note 4: 需要委托默认构造函数,见 Note 1。不委托无法通过 assert。assert(ichi == 1);assert(ein == nullptr);ichi = other.ichi;if (other.ein) {ein = new int[ichi] { other.ein[0] };}}// Note 5: 使用拷贝交换技术,需要实现 swap 的函数。// Note 6: swap 函数应当是 noexcept 的。friend void swap(Self& a, Self& b) noexcept {// Note 7: 交换成员对象时,可以优先使用类型自己定义的友元函数 swap,不存在才回退到 std::swap。using std::swap;swap(a.ichi, b.ichi);swap(a.ein, b.ein);}// Note 8: 移动构造函数应当是 noexcept 的。Demo(Self&& other) noexcept : Demo() { // Note 9: 需要委托默认构造函数,见 Note 1。不委托无法通过 assert。assert(ichi = 1);assert(ein == nullptr);swap(*this, other); // Note 10: 使用拷贝交换技术时,必须使用自己定义的友元函数,绝不要使用 std::swap。}// Note 11: 重载赋值运算符可以只写一个,且应当是 noexcept 的。异常在复制构造函数中发生,不在赋值运算符中发生。Self& operator=(Self other) noexcept {swap(*this, other); // Note 12: 使用拷贝交换技术时,必须使用自己定义的友元函数,绝不要使用 std::swap。return *this;}// Note 13: 析构函数是否是 constexpr 的,视情况而定。constexpr ~Demo() { // Note 14: 析构函数默认总是 noexcept 的,不写。if (ein) {delete[] ein;}}
};int main() {// 测试 constexpr 默认构造。constexpr Demo default_obj;static_assert(default_obj.ichi == 1);// 测试默认构造。Demo allocated_obj;allocated_obj.ein = new int[1] { 114514 };{// 测试复制构造。Demo test_copy_constructor = allocated_obj;assert(test_copy_constructor.ein[0] == 114514);assert(allocated_obj.ein[0] == 114514);// 测试移动构造。Demo test_move_constructor = std::move(test_copy_constructor);assert(test_move_constructor.ein[0] == 114514);assert(test_copy_constructor.ein == nullptr);}{// 测试复制赋值。Demo test_copy_assignment;test_copy_assignment = allocated_obj;assert(allocated_obj.ein[0] == 114514);// 测试移动赋值。Demo test_move_assignment;test_move_assignment = std::move(test_copy_assignment);assert(test_move_assignment.ein[0] == 114514);assert(test_copy_assignment.ein == nullptr);}
}
相关文章:

C++ 拷贝交换技术示例
拷贝交换技术(copy and swap)是什么,网上估计能查到很多。但网上有点难找到完整的演示代码,所以这里记录一下。难点在于: 如果要满足 5 的原则,我到底要写那些函数? 默认构造函数、复制构造函数…...
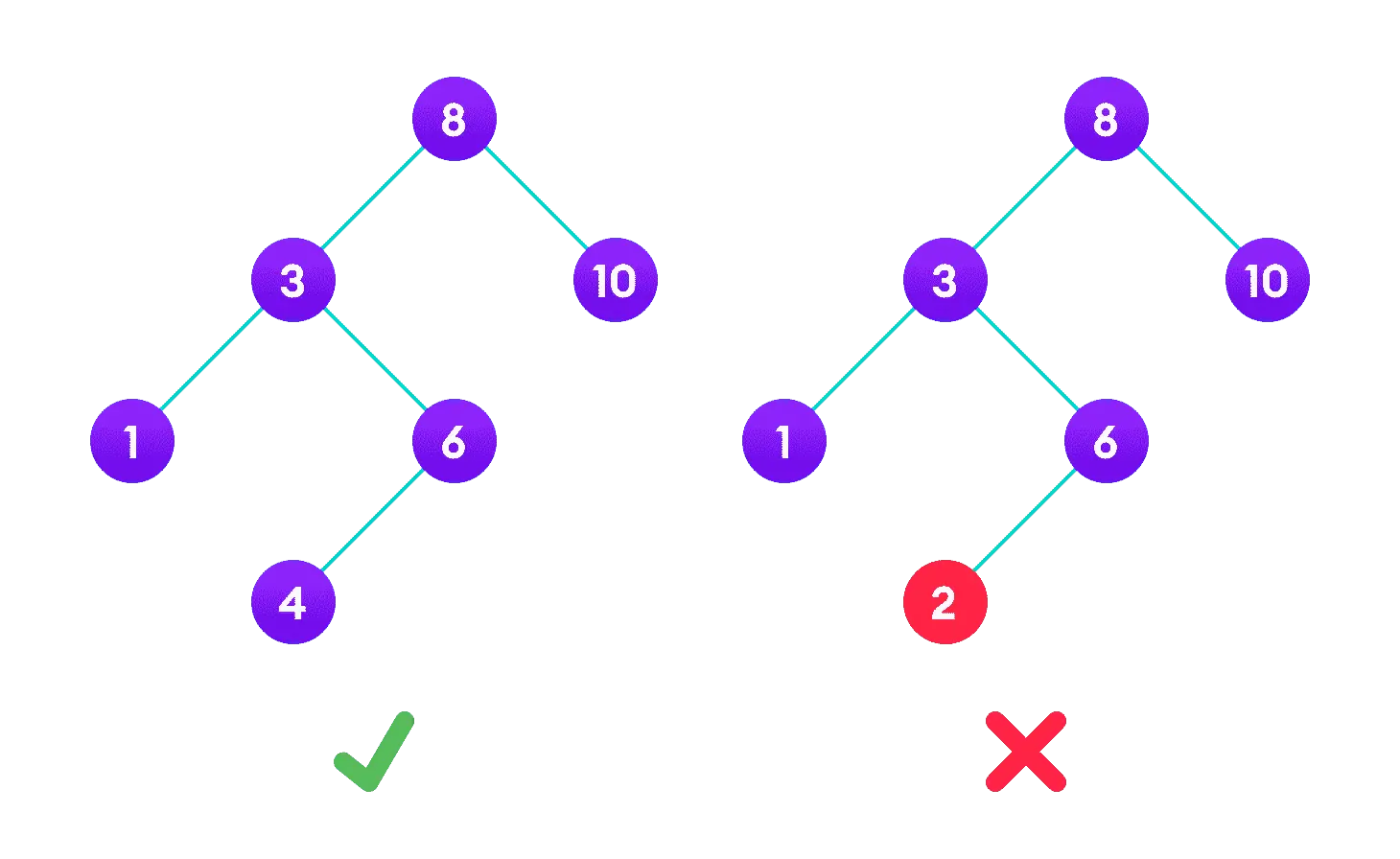
使用 Go 语言实现二叉搜索树
原文链接: 使用 Go 语言实现二叉搜索树 二叉树是一种常见并且非常重要的数据结构,在很多项目中都能看到二叉树的身影。 它有很多变种,比如红黑树,常被用作 std::map 和 std::set 的底层实现;B 树和 B 树,…...

系统接口自动化测试方案
XXX接口自动化测试方案 1、引言 1.1 文档版本 版本 作者 审批 备注 V1.0 XXXX 创建测试方案文档 1.2 项目情况 项目名称 XXX 项目版本 V1.0 项目经理 XX 测试人员 XXXXX,XXX 所属部门 XX 备注 1.3 文档目的 本文档主要用于指导XXX-Y…...
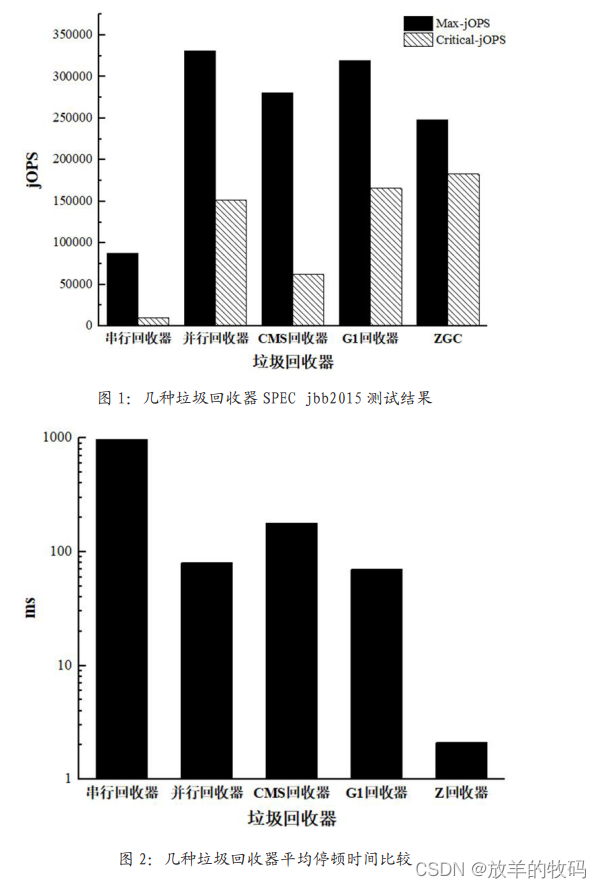
小研究 - JVM 垃圾回收方式性能研究(一)
本文从几种JVM垃圾回收方式及原理出发,研究了在 SPEC jbb2015基准测试中不同垃圾回收方式对于JVM 性能的影响,并通过最终测试数据对比,给出了不同应用场景下如何选择垃圾回收策略的方法。 目录 1 引言 2 垃圾回收算法 2.1 标记清除法 2.2…...
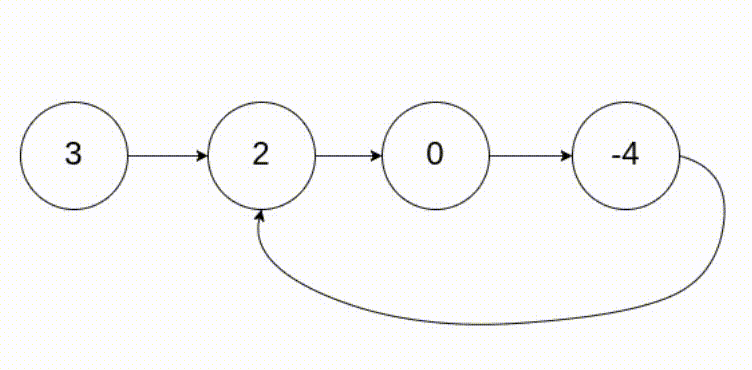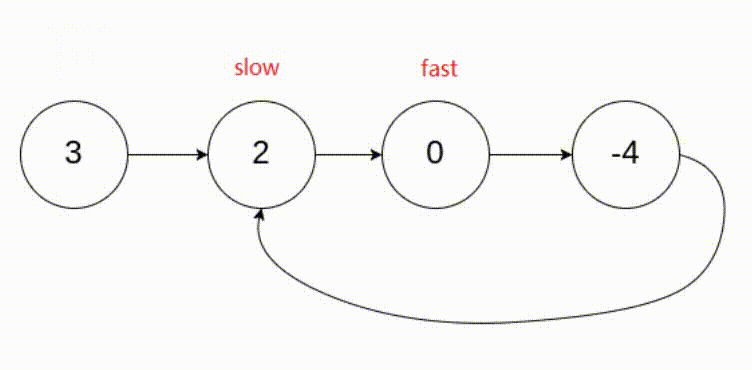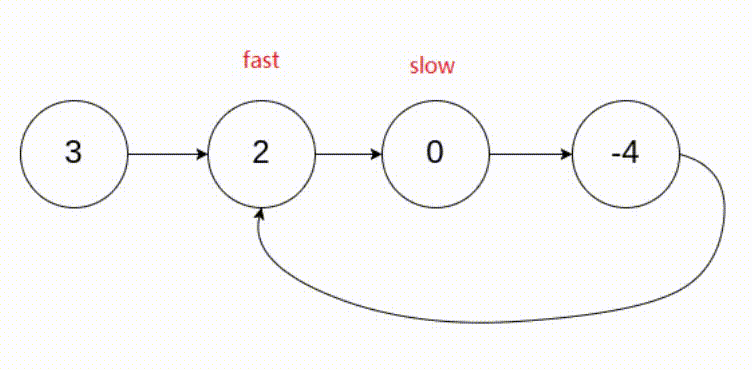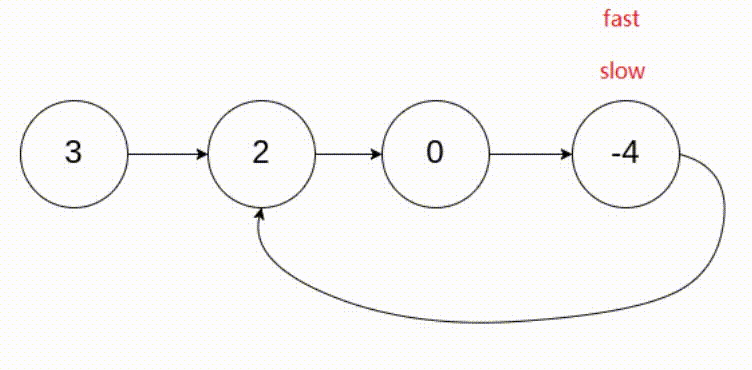
[LeetCode]链表相关题目(c语言实现)
文章目录 LeetCode203. 移除链表元素LeetCode237. 删除链表中的节点LeetCode206. 反转链表ⅠLeetCode92. 反转链表 II思路 1思路 2 LeetCode876. 链表的中间结点剑指 Offer 22. 链表中倒数第k个节点LeetCode21. 合并两个有序链表LeetCode86. 分隔链表LeetCode234. 回文链表Leet…...
] NAND 初始化常用命令:复位 (Reset) 和 Read ID 和 Read UID 操作和代码实现)
[深入理解NAND Flash (操作篇)] NAND 初始化常用命令:复位 (Reset) 和 Read ID 和 Read UID 操作和代码实现
依JEDEC eMMC及经验辛苦整理,原创保护,禁止转载。 专栏 《深入理解Flash:闪存特性与实践》 内容摘要 全文 4400 字,主要内容 复位的目的和作用? NAND Reset 种类:FFh, FCh, FAh, FDh 区别 Reset 操作步骤 和 代码实现 Read ID 操作步骤 和 代码实现 Read Uni…...

RxJava 复刻简版之二,调用流程分析之案例实现
接上篇:https://blog.csdn.net/da_ma_dai/article/details/131878516 代码节点:https://gitee.com/bobidali/lite-rx-java/commit/05199792ce75a80147c822336b46837f09229e46 java 类型转换 kt 类型: Any Object泛型: 协变: …...

SpringMVC中Model和ModelAndView的区别
SpringMVC中Model和ModelAndView的区别 两者的区别: 在SpringMVC中,Model和ModelAndView都是用于将数据传递到视图层的对象 Model是”模型“的意思,是MVC架构中的”M“部分,是用来传输数据的。 理解成MVC架构中的”M“和”V“…...
Tomcat安装与管理
文章目录 Tomcat安装及管理Tomcat gz包安装:JDK安装:Tomcat安装:修改配置文件(如下):服务启动配置: Tomcat-管理(部署jpress):修改允许访问的主机修改允许管理APP的主机进入管理&…...

React之路由
React之路由 背景: react: 18.2.0 路由:react-router-dom: 6.14.2 1、路由表配置 src下新建router/index.ts import React, { lazy } from react import { Navigate } from react-router-dom import Layout from /layout/Index import { JSX } from rea…...
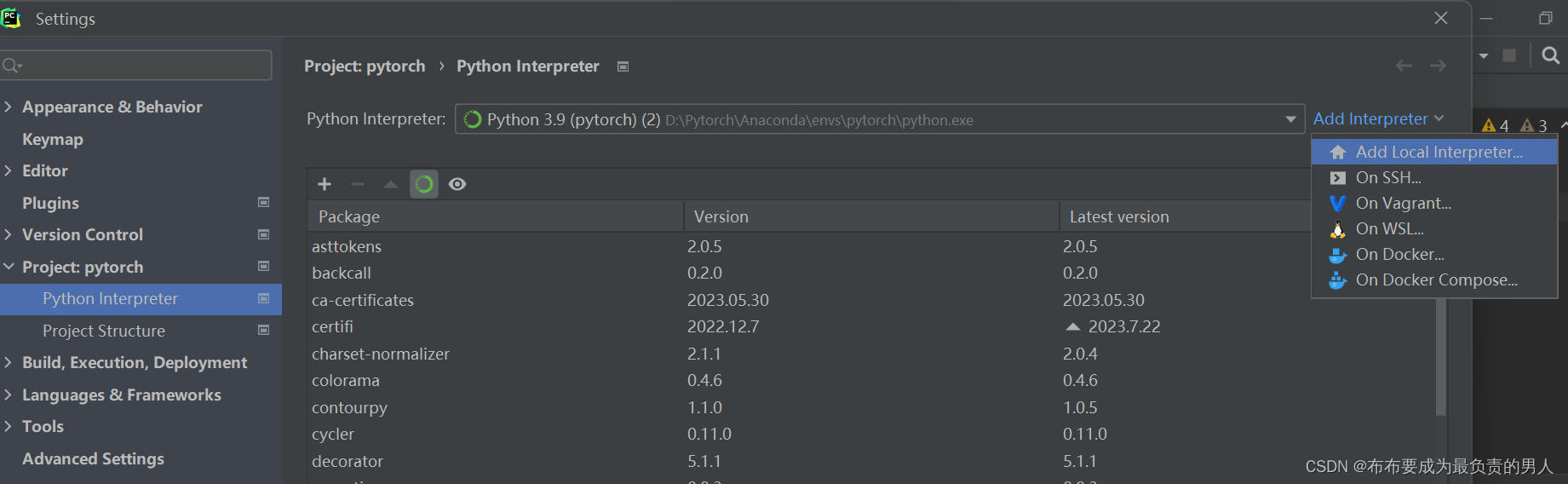
机器学习深度学习——非NVIDIA显卡怎么做深度学习(坑点排查)
👨🎓作者简介:一位即将上大四,正专攻机器学习的保研er 🌌上期文章:机器学习&&深度学习——数值稳定性和模型化参数(详细数学推导) 📚订阅专栏:机器…...

2021 Robocom 决赛 第四题
原题链接: PTA | 程序设计类实验辅助教学平台 题面: 在一个名叫刀塔的国家里,有一只猛犸正在到处跑着,希望能够用它的长角抛物技能来撞飞别人。已知刀塔国有 N 座城市,城市之间由 M 条道路互相连接,为了拦…...
线程池-手写线程池Linux C简单版本(生产者-消费者模型)
目录 简介手写线程池线程池结构体分析task_ttask_queue_tthread_pool_t 线程池函数分析thread_pool_createthread_pool_postthread_workerthread_pool_destroywait_all_donethread_pool_free 主函数调用 运行结果 简介 本线程池采用C语言实现 线程池的场景: 当某些…...

05-向量的意义_n维欧式空间
线性代数 什么是向量?究竟为什么引入向量? 为什么线性代数这么重要?从研究一个数拓展到研究一组数 一组数的基本表示方法——向量(Vector) 向量是线性代数研究的基本元素 e.g. 一个数: 666,…...

交通运输安全大数据分析解决方案
当前运输市场竞争激烈,道路运输企业受传统经营观念影响,企业管理者安全意识淡薄,从业人员规范化、流程化的管理水平较低,导致制度规范在落实过程中未能有效监督与管理,执行过程中出现较严重的偏差,其营运车…...
)
vimrc 配置 (持续跟新中)
vimrc 配置 #显示行号 set nu #自动换行 set autoindent #设置tab键 宽度为四个空格 set tabstop4 set shiftwidth4 set expandtab更多文章,详见我的博客网站...

【集成学习介绍】
1. 引言 在机器学习领域,集成学习(Ensemble Learning)是一种强大的技术,通过将多个弱学习器组合成一个更强大的集成模型,来提升模型的鲁棒性和性能。 2. 集成学习的原理 集成学习的核心思想是“三个臭皮匠ÿ…...

动画制作选择Blender还是Maya
Blender和Maya是两种最广泛使用的 3D 建模和动画应用程序。许多经验丰富的用户表示,Blender 在雕刻工具方面远远领先于 Maya,并且在 3D 建模方面达到了相同的质量水平。对于刚接触动画行业的人来说,您可能会问“我应该使用 Blender 还是 Maya…...
215. 数组中的第K个最大元素
题目链接:力扣 解题思路: 方法一:基于快速排序 因为题目中只需要找到第k大的元素,而快速排序中,每一趟排序都可以确定一个最终元素的位置。 当使用快速排序对数组进行降序排序时,那么如果有一趟排序过程…...

NLP From Scratch: 生成名称与字符级RNN
NLP From Scratch: 生成名称与字符级RNN 这是我们关于“NLP From Scratch”的三个教程中的第二个。 在<cite>第一个教程< / intermediate / char_rnn_classification_tutorial ></cite> 中,我们使用了 RNN 将名称分类为来源语言。 这次ÿ…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...

【大厂机试题解法笔记】矩阵匹配
题目 从一个 N * M(N ≤ M)的矩阵中选出 N 个数,任意两个数字不能在同一行或同一列,求选出来的 N 个数中第 K 大的数字的最小值是多少。 输入描述 输入矩阵要求:1 ≤ K ≤ N ≤ M ≤ 150 输入格式 N M K N*M矩阵 输…...
