剑指offer 动态规划篇
题目由入门往上递增
入门
斐波那契数列_牛客题霸_牛客网 (nowcoder.com)
动态规划甚至于算法的入门题目
方法一:按照斐波那契的公式fn=fn-1+fn-2,从1-n求出结果。
class Solution {
public:int Fibonacci(int n) {vector<int>f={0,1,1};for(int i=3;i<=n;i++)f.push_back(f[i-1]+f[i-2]);return f[n];}
};方法二:按照公式倒推,即用递归求出。
class Solution {
public:int Fibonacci(int n) {if(n==1||n==2) return 1;return Fibonacci(n-1)+Fibonacci(n-2);}
};简单
连续子数组的最大和_牛客题霸_牛客网 (nowcoder.com)
我们令dp[i]是以第i个数为结尾的子数组和的最大值。如果dp[i-1]为负,则以i-1为结尾的子数组和都为负,因此以dp[i]结果就是第i个数的值,除此之外是dp[i-1]+第i个数。
因此转移公式得出
验证:假设以i为结尾的子数组和的最大值是r到l,则以r-1为结尾的子数组和一定为负数,和我们的推导符合。
class Solution {public:int FindGreatestSumOfSubArray(vector<int> array) {int sum=0;int maxx=array[0];sum=array[0];for(int i=1;i<array.size();i++){sum=max(sum+array[i],array[i]);maxx=max(sum,maxx);}return maxx;}
};跳台阶_牛客题霸_牛客网 (nowcoder.com)
台阶n可以由n-1跳一步或n-2跳一步得到,因此就是斐波那契数列。.
class Solution {
public:int jumpFloor(int number) {if(number==1) return 1;if(number==2) return 2;return jumpFloor(number-1)+jumpFloor(number-2);}
};跳台阶扩展问题_牛客题霸_牛客网 (nowcoder.com)
和上一题类似,只不过通项公式变为了fn=fn-1+……f1,求fn
因此这时候我们考虑高斯消元……
开个玩笑,上述公式可以变化为fn=fn-1*2;
问题解决
class Solution {
public:int jumpFloorII(int number) {if (number==1) {return 1;}return jumpFloorII(number-1)*2;}
};买卖股票的最好时机(一)_牛客题霸_牛客网 (nowcoder.com)
因为只能买卖一次,如果在第k天卖出,就是要求第k天前最小值的买入
也可以dp,太麻烦了没必要。
class Solution {
public:int maxProfit(vector<int>& prices) {int ans=0;int minn=prices[0];for(int i=1;i<prices.size();i++){minn=min(minn,prices[i]);ans=max(prices[i]-minn,ans);}return ans;}
};中等
连续子数组的最大和(二)_牛客题霸_牛客网 (nowcoder.com)
对于dp方面思路同上,此时只是需要在sum小于0的时候更新l1,在maxx更新的时候维护l和r(l为l1,r为i)
class Solution {public:vector<int> FindGreatestSumOfSubArray(vector<int>& array) {int sum = 0;int maxx = array[0];int l=0,r=0,l1=0;sum = array[0];for (int i = 1; i < array.size(); i++) {if(sum<0){l1=i;}sum = max(sum + array[i], array[i]);if(maxx<=sum){l=l1;r=i;}maxx = max(sum, maxx);}vector<int>ans;for(int i=l;i<=r;i++){ans.push_back(array[i]);}return ans;}
};矩形覆盖_牛客题霸_牛客网 (nowcoder.com)
通过观察可以得出构成方式只有一竖和两横两种情况,因此有n块肯定是n-1加上一块竖的或者n-2加上两条横的(此时两条竖的已经被上一种情况包含了),因此是斐波那契数列
class Solution {
public:int rectCover(int number) {if(number==0) return 0;if(number==1)return 1;if(number==2) return 2;return rectCover(number-1)+rectCover(number-2);}
};礼物的最大价值_牛客题霸_牛客网 (nowcoder.com)
最后一格的最大值是它左边和上面的最大值的较大值加上自己,因而只能往右和往下,所以保证了每个格子只会被走一次,无后效性。
此时注意最上面和最左边只有一种走法,可以扩大一格dp数组或者预处理。
class Solution {
public:int maxValue(vector<vector<int> >& grid) {int dp[202][202];dp[0][0]=grid[0][0];for(int j=1;j<grid[0].size();j++){dp[0][j]=grid[0][j]+dp[0][j-1];}for(int j=1;j<grid.size();j++){dp[j][0]=grid[j][0]+dp[j-1][0];}for(int i=1;i<grid.size();i++){for(int j=1;j<grid[0].size();j++){dp[i][j]=max(dp[i-1][j],dp[i][j-1])+grid[i][j];cout<<dp[i][j]<<" ";}}return dp[grid.size()-1][grid[0].size()-1];}
};最长不含重复字符的子字符串_牛客题霸_牛客网 (nowcoder.com)
设置滑动窗口,记录窗口内的字符,如果下一个进来会重复,就将l往后移直到不重复。记录窗口最大值。
class Solution {
public:int lengthOfLongestSubstring(string s) {vector<int> a(128,0);int l=0,r=0,len=s.size();int ans=0;while(r<len){int temp=s[r];while(a[temp]==1){int x=s[l];a[x]--;l++;}a[temp]++;cout<<temp<<" "<<a[temp]<<" "<<r-l<<"\n";ans=max(ans,r-l+1);r++;}return ans;}
};把数字翻译成字符串_牛客题霸_牛客网 (nowcoder.com)
这题比较烦躁的是要判断一堆乱七八糟无解的情况,反正特判一下。
存在多种编码的情况就是12、26这种,既可以拆分也可以合并。因为字母编码最长为两位,所以dpi的结果是dpi-1加一位或者dpi-2加两位(此时要判断是否合法)因此就是dpi-1+dpi-2。
class Solution {
public:int solve(string nums) {if(nums=="0")return 0; vector<int>ans(100,0);ans[0]=1;if((nums[0]=='1'&&nums[1]!='0')||(nums[0]=='2'&&nums[1]<='6'&&nums[1]>'0')) ans[1]=2;else ans[1]=1;for(int i = 1; i < nums.length(); i++){ if(nums[i] == '0')if(nums[i - 1] != '1' && nums[i - 1] != '2')return 0;}for(int i=2;i<nums.size();i++){if((nums[i-1]=='1'&&nums[i]!='0')||(nums[i-1]=='2'&&nums[i]<='6'&&nums[i]>'0')){ans[i]=ans[i-2]+ans[i-1];}else ans[i]=ans[i-1];}return ans[nums.size()-1];}
};正则表达式匹配_牛客题霸_牛客网 (nowcoder.com)
又是蛇皮烦的一题……
首先,还是设置dp数组,dpij代表str第i位结尾、pattern第j位结尾的子字符串能否匹配。假设第i-1
位和第j-1位能成功匹配,那么此时就是要对比第i位和第j位字符关系,如果两个都是小写字母,且相同,那么dpij的结果就是dpi-1j-1的结果。如果不符合可以直接判断为false。
因此第j位如果是.代表着任意字符,所以转移公式可以等同于上面的情况。
接下来就是考虑第j位为*的情况,此时要把第j-1位一同考虑,当作整体,下面将j-1视作a。
第一种情况是假定*为0次,此时dpij的结果就和dpij-2的结果相同。
第二种情况是假定*为1次,因为如果前面*已经被当成a的话此时已经成功匹配了,可以忽略了,后面同理。假定为一次的话j-1就要等同于i,*才能变成第i位进行匹配,那么此时的转移公式就是dpij=dpi-1j
第一种情况和第二种情况可以同时存在,符合条件的时候取或就行。
#include <vector>
class Solution {bool match(string str, string pattern) {vector<vector<int> >dp;vector<int> temp(30, 0);dp.resize(30, temp);dp[0][0] = 1;for (int i = 1; i <= pattern.size(); i++) {if (pattern[i]=='*')dp[0][i+1]=dp[0][i-1];}for (int i = 0; i < str.size(); i++) {for (int j = 0; j < pattern.size(); j++) {if (str[i] == pattern[j] || pattern[j] == '.') {dp[i + 1][j + 1] = dp[i][j];} else {if (pattern[j] == '*') {dp[i+1][j+1]=dp[i+1][j-1];if(pattern[j-1]=='.'||pattern[j-1]==str[i]){dp[i+1][j+1]=dp[i][j+1]||dp[i+1][j+1];}}}}}if (dp[str.size()][pattern.size()] == 1)return true;else return false;}
};相关文章:

剑指offer 动态规划篇
题目由入门往上递增 入门 斐波那契数列_牛客题霸_牛客网 (nowcoder.com) 动态规划甚至于算法的入门题目 方法一:按照斐波那契的公式fnfn-1fn-2,从1-n求出结果。 class Solution { public:int Fibonacci(int n) {vector<int>f{0,1,1};for(int …...
自动化部署的一些笔记)
关于Linux中前端负载均衡之VIP(LVS+Keepalived)自动化部署的一些笔记
写在前面 整理一些 LVS 相关的笔记理解不足小伙伴帮忙指正 傍晚时分,你坐在屋檐下,看着天慢慢地黑下去,心里寂寞而凄凉,感到自己的生命被剥夺了。当时我是个年轻人,但我害怕这样生活下去,衰老下去。在我看来…...

C++ 拷贝交换技术示例
拷贝交换技术(copy and swap)是什么,网上估计能查到很多。但网上有点难找到完整的演示代码,所以这里记录一下。难点在于: 如果要满足 5 的原则,我到底要写那些函数? 默认构造函数、复制构造函数…...
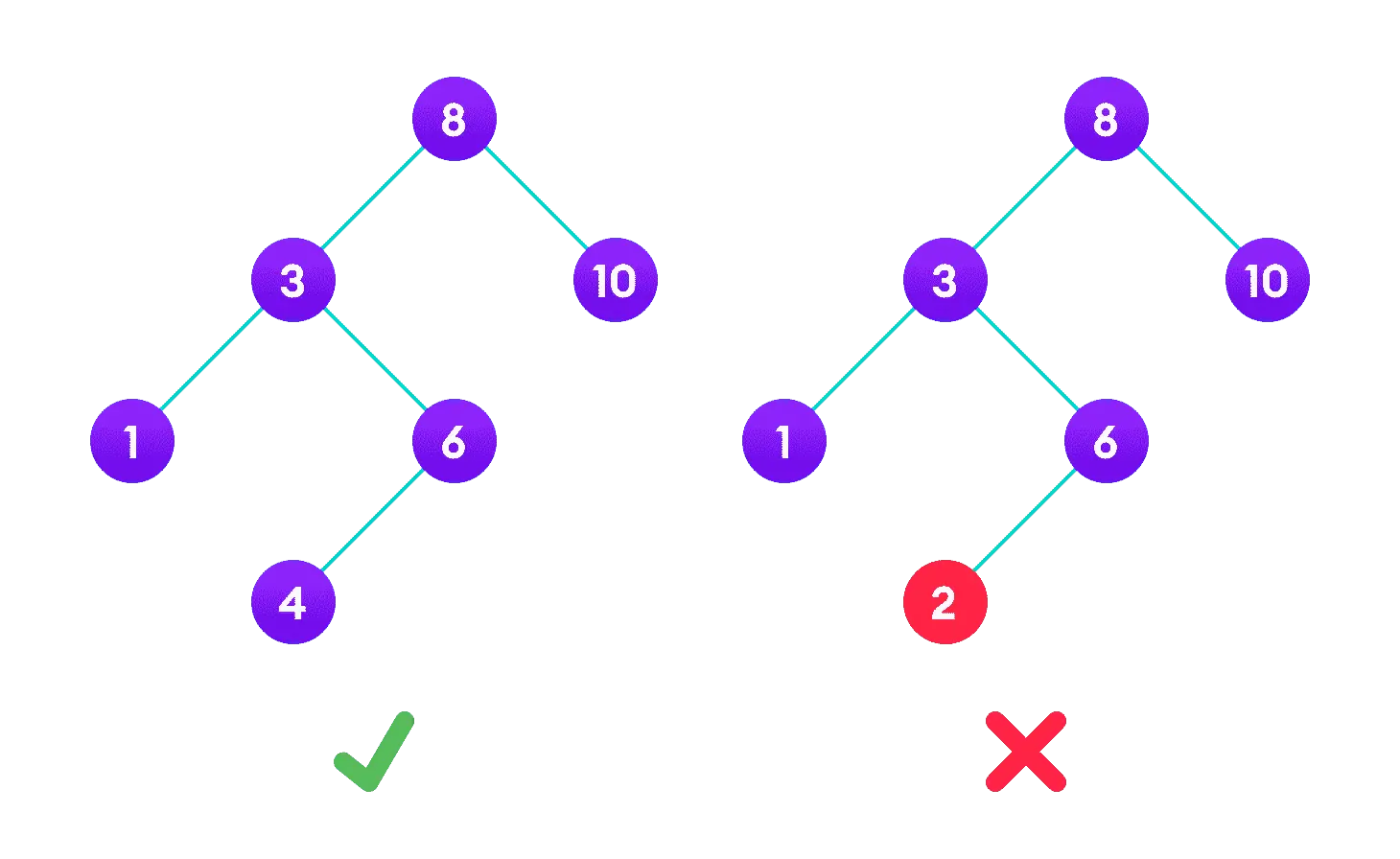
使用 Go 语言实现二叉搜索树
原文链接: 使用 Go 语言实现二叉搜索树 二叉树是一种常见并且非常重要的数据结构,在很多项目中都能看到二叉树的身影。 它有很多变种,比如红黑树,常被用作 std::map 和 std::set 的底层实现;B 树和 B 树,…...

系统接口自动化测试方案
XXX接口自动化测试方案 1、引言 1.1 文档版本 版本 作者 审批 备注 V1.0 XXXX 创建测试方案文档 1.2 项目情况 项目名称 XXX 项目版本 V1.0 项目经理 XX 测试人员 XXXXX,XXX 所属部门 XX 备注 1.3 文档目的 本文档主要用于指导XXX-Y…...
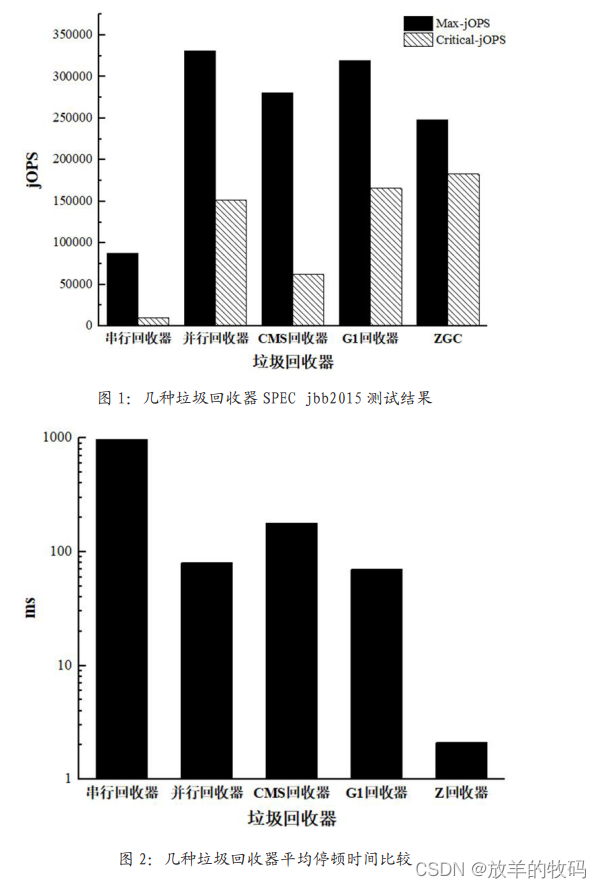
小研究 - JVM 垃圾回收方式性能研究(一)
本文从几种JVM垃圾回收方式及原理出发,研究了在 SPEC jbb2015基准测试中不同垃圾回收方式对于JVM 性能的影响,并通过最终测试数据对比,给出了不同应用场景下如何选择垃圾回收策略的方法。 目录 1 引言 2 垃圾回收算法 2.1 标记清除法 2.2…...
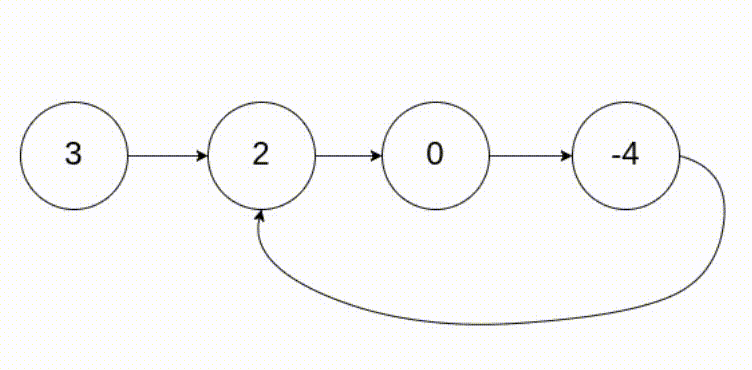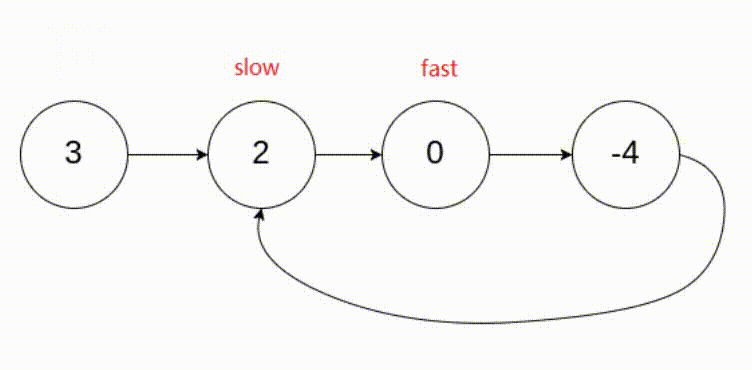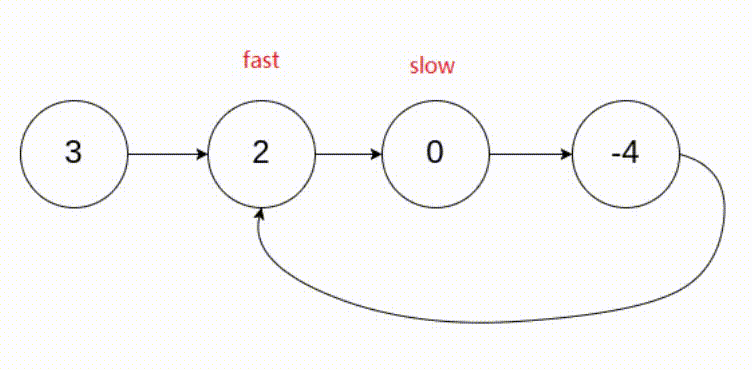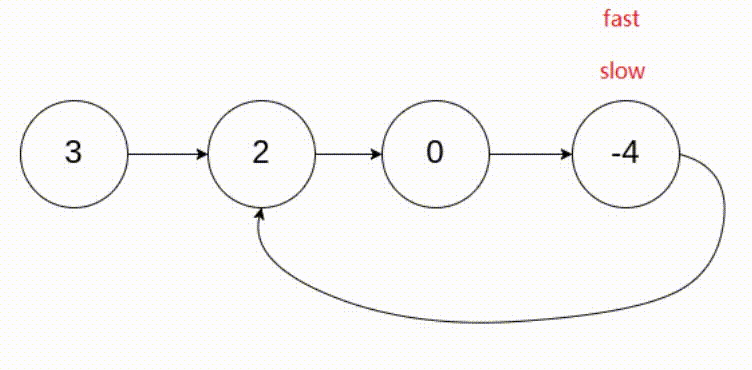
[LeetCode]链表相关题目(c语言实现)
文章目录 LeetCode203. 移除链表元素LeetCode237. 删除链表中的节点LeetCode206. 反转链表ⅠLeetCode92. 反转链表 II思路 1思路 2 LeetCode876. 链表的中间结点剑指 Offer 22. 链表中倒数第k个节点LeetCode21. 合并两个有序链表LeetCode86. 分隔链表LeetCode234. 回文链表Leet…...
] NAND 初始化常用命令:复位 (Reset) 和 Read ID 和 Read UID 操作和代码实现)
[深入理解NAND Flash (操作篇)] NAND 初始化常用命令:复位 (Reset) 和 Read ID 和 Read UID 操作和代码实现
依JEDEC eMMC及经验辛苦整理,原创保护,禁止转载。 专栏 《深入理解Flash:闪存特性与实践》 内容摘要 全文 4400 字,主要内容 复位的目的和作用? NAND Reset 种类:FFh, FCh, FAh, FDh 区别 Reset 操作步骤 和 代码实现 Read ID 操作步骤 和 代码实现 Read Uni…...

RxJava 复刻简版之二,调用流程分析之案例实现
接上篇:https://blog.csdn.net/da_ma_dai/article/details/131878516 代码节点:https://gitee.com/bobidali/lite-rx-java/commit/05199792ce75a80147c822336b46837f09229e46 java 类型转换 kt 类型: Any Object泛型: 协变: …...

SpringMVC中Model和ModelAndView的区别
SpringMVC中Model和ModelAndView的区别 两者的区别: 在SpringMVC中,Model和ModelAndView都是用于将数据传递到视图层的对象 Model是”模型“的意思,是MVC架构中的”M“部分,是用来传输数据的。 理解成MVC架构中的”M“和”V“…...
Tomcat安装与管理
文章目录 Tomcat安装及管理Tomcat gz包安装:JDK安装:Tomcat安装:修改配置文件(如下):服务启动配置: Tomcat-管理(部署jpress):修改允许访问的主机修改允许管理APP的主机进入管理&…...

React之路由
React之路由 背景: react: 18.2.0 路由:react-router-dom: 6.14.2 1、路由表配置 src下新建router/index.ts import React, { lazy } from react import { Navigate } from react-router-dom import Layout from /layout/Index import { JSX } from rea…...
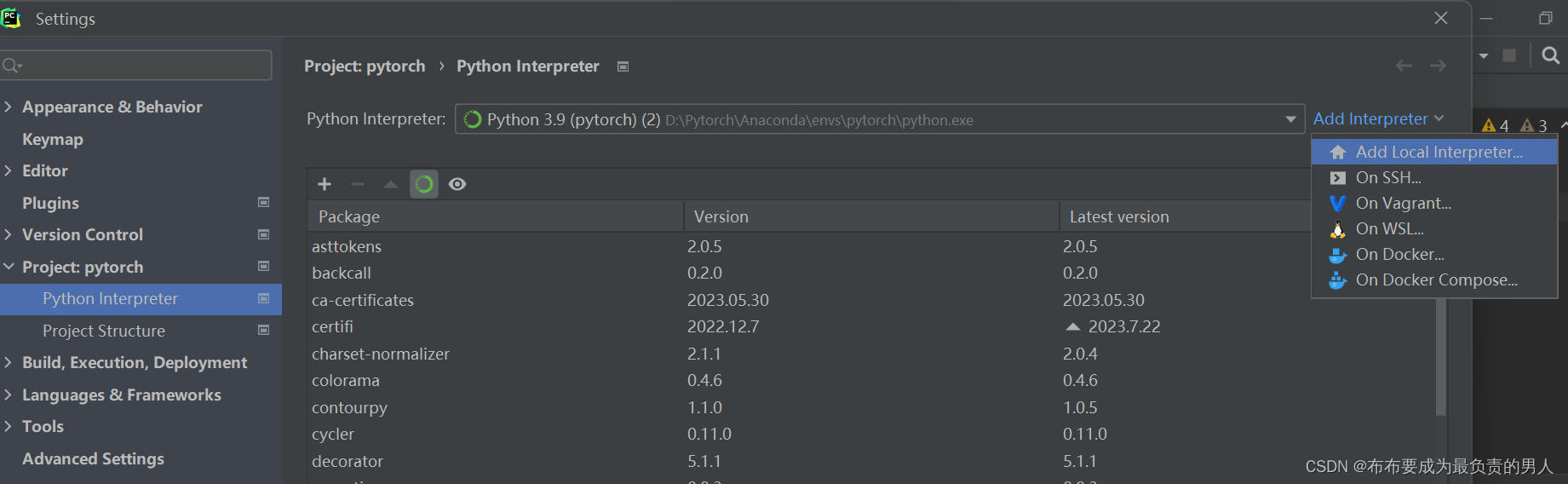
机器学习深度学习——非NVIDIA显卡怎么做深度学习(坑点排查)
👨🎓作者简介:一位即将上大四,正专攻机器学习的保研er 🌌上期文章:机器学习&&深度学习——数值稳定性和模型化参数(详细数学推导) 📚订阅专栏:机器…...

2021 Robocom 决赛 第四题
原题链接: PTA | 程序设计类实验辅助教学平台 题面: 在一个名叫刀塔的国家里,有一只猛犸正在到处跑着,希望能够用它的长角抛物技能来撞飞别人。已知刀塔国有 N 座城市,城市之间由 M 条道路互相连接,为了拦…...
线程池-手写线程池Linux C简单版本(生产者-消费者模型)
目录 简介手写线程池线程池结构体分析task_ttask_queue_tthread_pool_t 线程池函数分析thread_pool_createthread_pool_postthread_workerthread_pool_destroywait_all_donethread_pool_free 主函数调用 运行结果 简介 本线程池采用C语言实现 线程池的场景: 当某些…...

05-向量的意义_n维欧式空间
线性代数 什么是向量?究竟为什么引入向量? 为什么线性代数这么重要?从研究一个数拓展到研究一组数 一组数的基本表示方法——向量(Vector) 向量是线性代数研究的基本元素 e.g. 一个数: 666,…...

交通运输安全大数据分析解决方案
当前运输市场竞争激烈,道路运输企业受传统经营观念影响,企业管理者安全意识淡薄,从业人员规范化、流程化的管理水平较低,导致制度规范在落实过程中未能有效监督与管理,执行过程中出现较严重的偏差,其营运车…...
)
vimrc 配置 (持续跟新中)
vimrc 配置 #显示行号 set nu #自动换行 set autoindent #设置tab键 宽度为四个空格 set tabstop4 set shiftwidth4 set expandtab更多文章,详见我的博客网站...

【集成学习介绍】
1. 引言 在机器学习领域,集成学习(Ensemble Learning)是一种强大的技术,通过将多个弱学习器组合成一个更强大的集成模型,来提升模型的鲁棒性和性能。 2. 集成学习的原理 集成学习的核心思想是“三个臭皮匠ÿ…...

动画制作选择Blender还是Maya
Blender和Maya是两种最广泛使用的 3D 建模和动画应用程序。许多经验丰富的用户表示,Blender 在雕刻工具方面远远领先于 Maya,并且在 3D 建模方面达到了相同的质量水平。对于刚接触动画行业的人来说,您可能会问“我应该使用 Blender 还是 Maya…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...
