环形链表的进一步探究

茕茕白兔,东走西顾,衣不如新,人不如故
往期回顾:
数据结构——双向链表
数据结构——单链表
数据结构——顺序表
文章目录
如何判断一个链表是否为环形链表
环形链表的判断的深入探究
例1:沸羊羊追美羊羊
例2:灰太狼追懒羊羊
判断方法结论总结
环形链表的入口结点
源码及思路
另辟蹊径
大家好,我是纪宁。这篇文章将深入探究环形链表。
环形链表的形成是因为当单链表最后一个结点的指针域没有指向空,而指向了前面的任意一个结点。单链表链表一旦成环,在遍历的时候就会造成在一个区域里循环,那么对于环形链表的探究也应运而生。
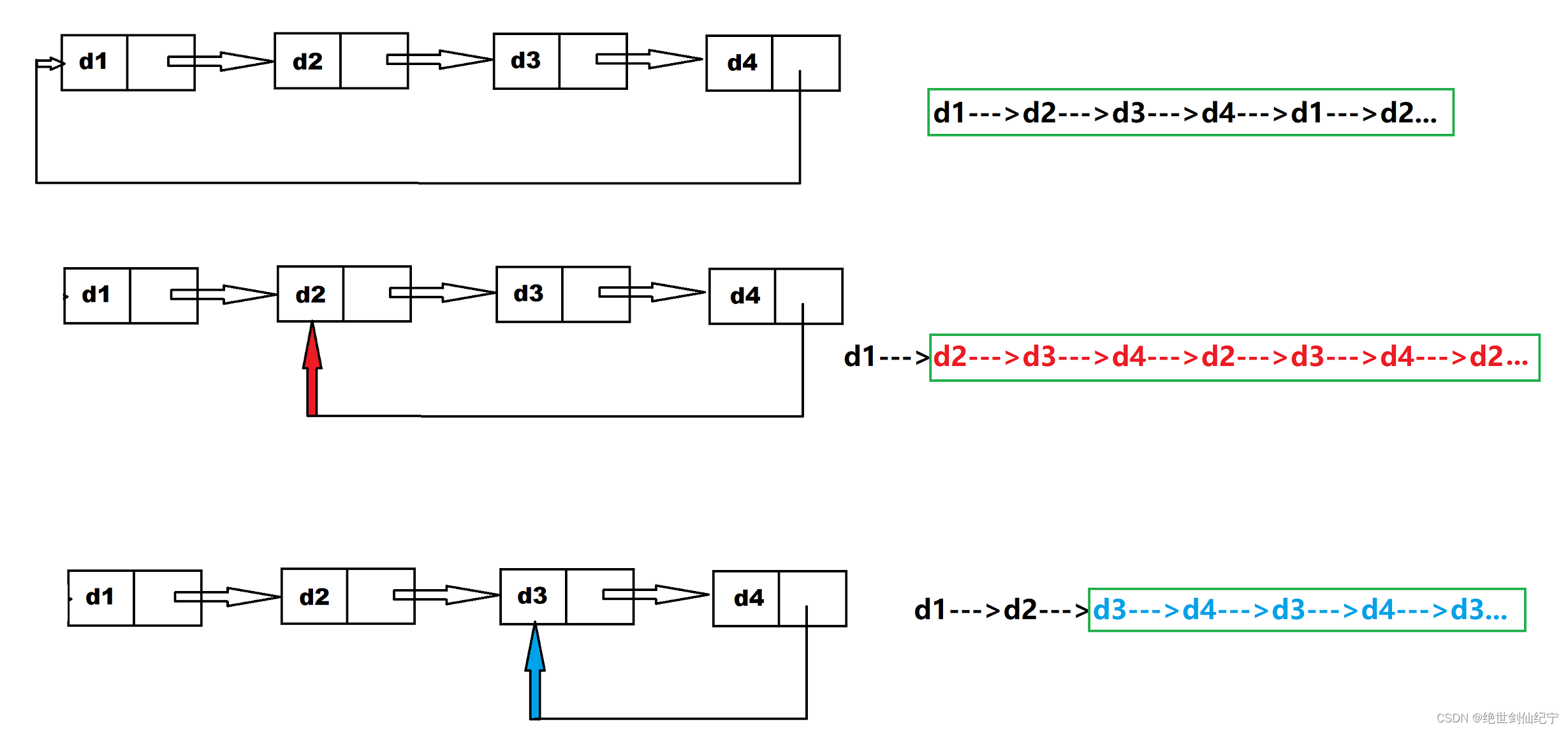
在现实情况中,链表不可能这么短,所以如何判断链表是否成环,链表在何处成环,就成为了我们学习链表之后必须要研究的问题,也成为了面试题和笔试题中最喜欢考察的部分。
在上一篇链表刷题总结快慢指针的时候,博主曾粗略的谈到了环形链表的概念。这篇文章,博主带大家深入探究并总结,也算是博主自我内核的进一步提升吧。上篇文章的链接:快慢指针
如何判断一个链表是否为环形链表
首先,要明白环形链表的特征,如果定义一个指针去维护环形链表,它会在特定的位置进入环形链表内部,然后一直在环形链表内部循环遍历,这里如果使用快慢指针的话,在思路上是比较好理解的:当一个快指针和一个慢指针一起从头结点往后走,如果链表存在环,那么快指针首先进入环中,而慢指针则后入环,快指针在一直绕环循环的时候,一定能追上慢指针。如果没有追上的话,说明快指针一直向后走,直到 NULL,则说明这个链表不是环形指针。
代码如下
bool hasCycle(struct ListNode *head) {struct ListNode *slow=head;struct ListNode *fast=head;while(fast&&fast->next){slow=slow->next;fast=fast->next->next;if(fast==slow)return true;}return false;
}此代码将快指针定义为 fast ,慢指针定义为 slow,快指针每次向连链表末走两格,慢指针每次向链表末走一格(这里的走几格意思就是指针指向当前结点的后第几个结点),当两个指针相遇的时候,就说明这个链表带环。
环形链表的判断的深入探究
上段文章提到,快指针每次走两格,慢指针每次走一格,这里我们不禁有一些思考:真的能恰好追上吗?不会正好错过了吗?当快指针每次走三格,慢指针每次走一格呢?分析下面这几个例子。
例1:沸羊羊追美羊羊

沸羊羊跑的比较快,那么在无止尽的环中,它和美羊羊真的能正好相遇吗?
假设当美羊羊进入环中的时候,早已进入环中的沸羊羊和美羊羊在圆周上的距离为 N,而沸羊羊一次走的距离为 2,美羊羊一次走的距离为 1,沸羊羊每次比美羊羊多走的距离为 1 。
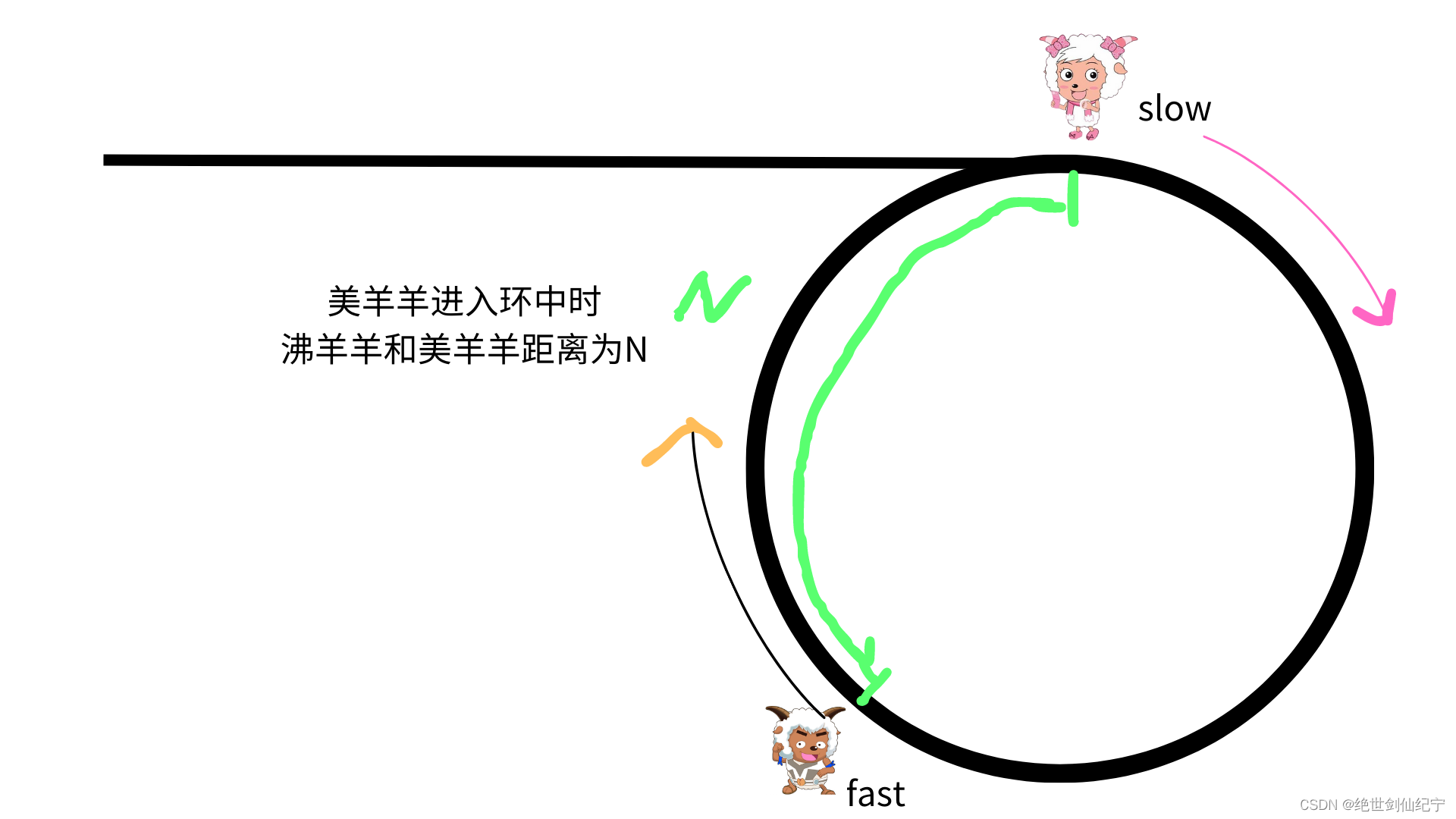
走 1 次后,他们俩之间的距离为 N-1
走 2 次后,他们俩之间的距离为 N-2
......
走 N-2 次后,他们俩之间的距离为 2
走 N-1 次后,他们俩之间的距离为 1
走 N 次后,他们俩之间的距离就为0,沸羊羊成功完美追上了美羊羊。
即使追上了,美羊羊就会接受沸羊羊吗?(开个玩笑)
这个例子说明了,快指针每次走两格,慢指针每次每次走一格,确实能相遇,可以用来判断环形链表,那么如果快指针每次走三格呢?
例2:灰太狼追懒羊羊
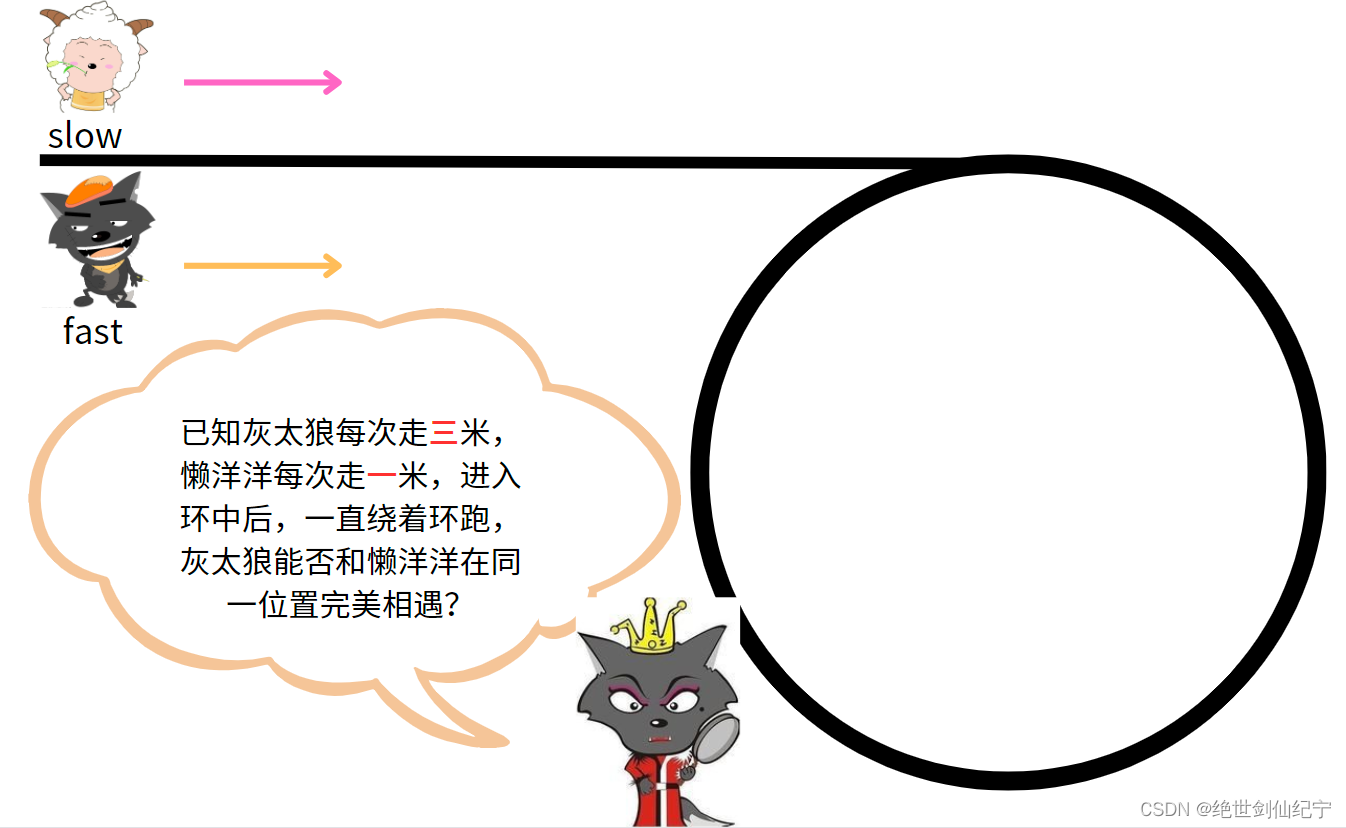
众所周知,红太狼爱吃羊,却从来没吃到过,但她有一个最疼爱她的老公灰太狼。灰太狼每天日复一日的想要抓到羊讨老婆换新,其中他最爱抓的羊,也是他觉得最好抓的羊,就是懒洋洋。
灰太狼和懒洋洋同时出发,灰太狼每次走三格,懒洋洋每次走一格,他们能完美相遇吗?
当懒洋洋进入环中时,灰太狼和它的举例为 M,环的长度为C,而懒洋洋每次走的距离为 1,灰太狼每次走的距离为 3,灰太狼比懒洋洋每次多走2灰太狼能否和懒洋洋完美相遇并抓到懒洋洋呢?
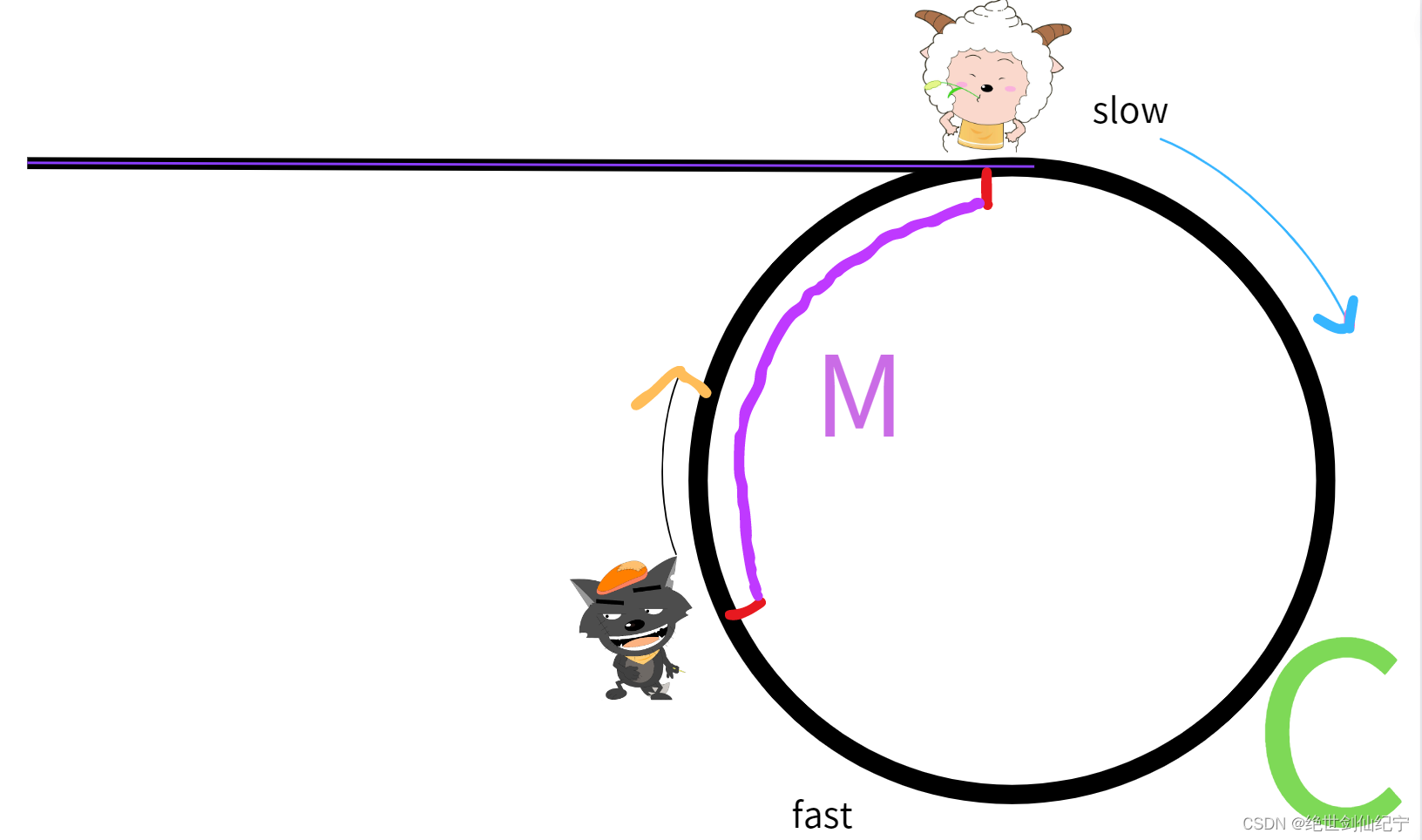 这种情况就和上面沸羊羊追美羊羊不一样了,无论沸羊羊和美羊羊距离多远,每次距离缩小1,总有一天距离会变为0。但灰太狼每次和懒洋洋的距离缩小 2,是否还会出现一直完美错过的情况。
这种情况就和上面沸羊羊追美羊羊不一样了,无论沸羊羊和美羊羊距离多远,每次距离缩小1,总有一天距离会变为0。但灰太狼每次和懒洋洋的距离缩小 2,是否还会出现一直完美错过的情况。
假设灰太狼和懒洋洋之间的距离 M 为偶数,那么之间每次的距离为
M-2
M-4
......
2
0
这种情况是一定能追上的。
那么如果他们之间的距离 M 为奇数,那么他们之间每次的距离为
M-2
M-2
......
3
1
-1
当距离为-1时,灰太狼跑到了懒洋洋前面,那么灰太狼就刚好错过了懒洋洋,要进行下一圈追击。并且追击的距离与环的周长C有关,因为这次要追击的距离为 C-1。
当 C-1 为偶数,即周长C为偶数时,则恰好可以追上懒洋洋,如果C-1 依然为奇数,即周长C为偶数时,那这次也追不上懒洋洋了。因为这次追击的距离为奇数,所以下次追击的距离依然为 C-1 为奇数,这就成了一个死循环,这种情况下灰太狼就永远也抓不到懒洋洋!
判断方法结论总结
当快指针每次走两步,慢指针每次走一步的时候,这两个指针一定能相遇,这种方法可以判断出链表是否为环形链表。
当快指针每次走三步,慢指针每次走一步的时候,这两个指针是否相遇得取决于进入环中时两指针的距离,当这个距离为偶数时,则一定能相遇;当这个距离为奇数时,还要看环的周长,如果环的周长为奇数时,则可以相遇,当环的长度为偶数时,则永远不能相遇。这种方法不一定能判断出链表是否为环形链表。
当快指针每次走四步时,会有更复杂的情况......
环形链表的入口结点
当我们判断出了一个链表是否为环形链表的时候,还会思考,那这个链表是在哪个结点开始进入环的呢?
从上面那个例子中可以得出,快指针每次走两格,慢指针每次走一格,快指针一定能追上慢指针,可以判断出链表是否带环。
继续说美羊羊和沸羊羊那个例子,从上面的例子可以得之,当美羊羊进入环中时,沸羊羊一定能在一圈之内追上美羊羊。
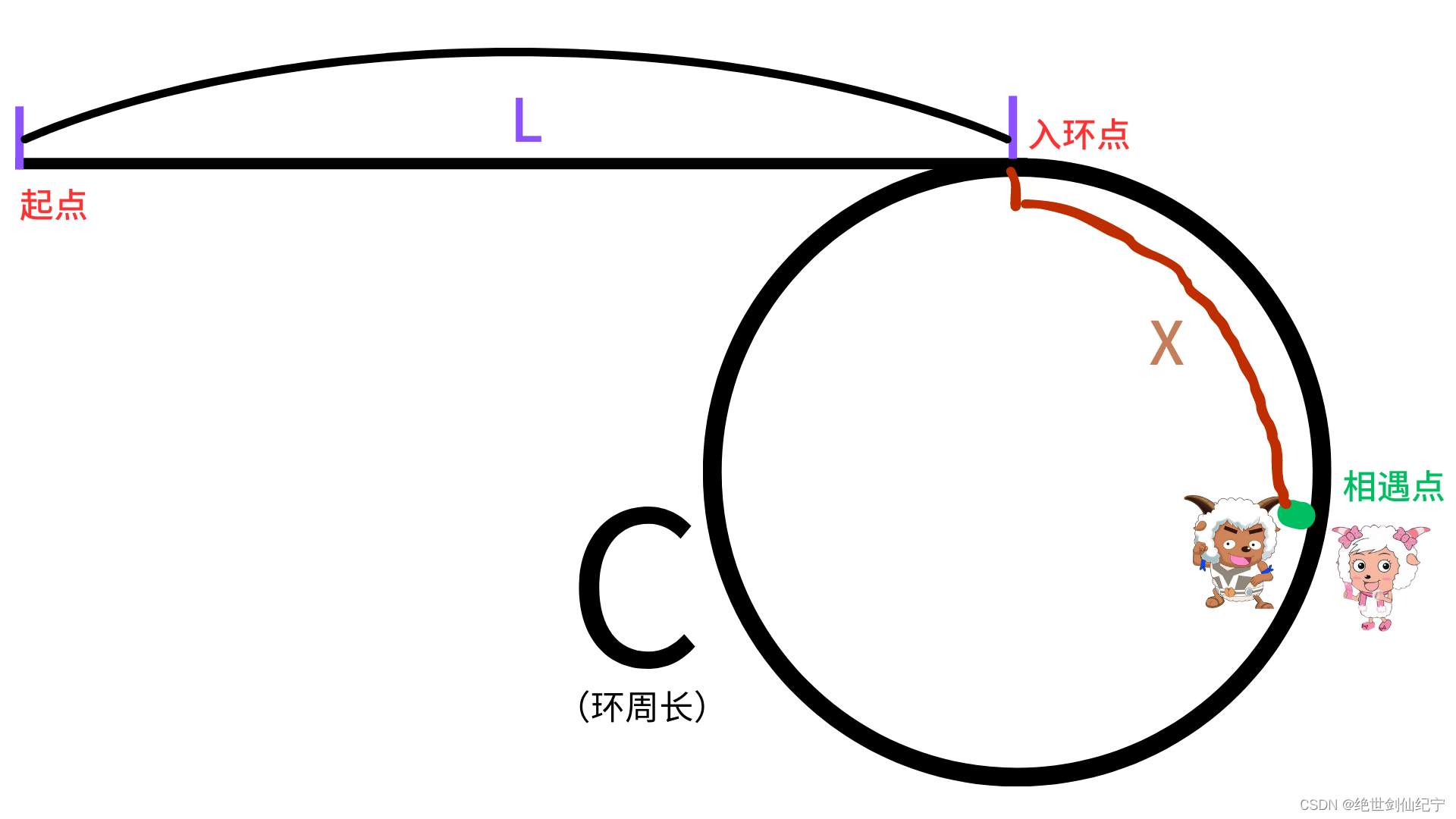
设环的周长为4,环前面的链表长度为 L ,沸羊羊和美羊羊的相遇点与入环点的距离为 X,因为沸羊羊在美羊羊入环前可能已经绕环好几圈了,就设沸羊羊在和美羊羊相遇前已经在环里走了N 圈。
沸羊羊的速度是美羊羊的 2 倍,所以他们走的距离也是 2 倍关系
美羊羊走的距离为
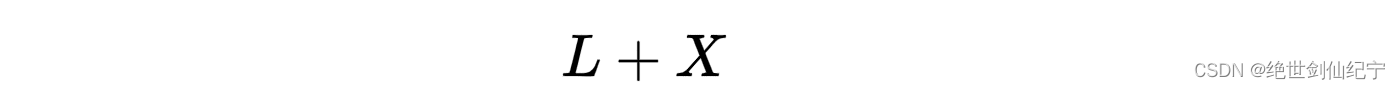
沸羊羊走的距离为
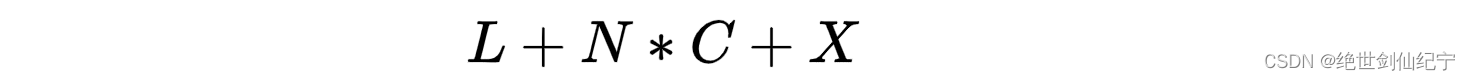
列出等式为

得出 L 的值为
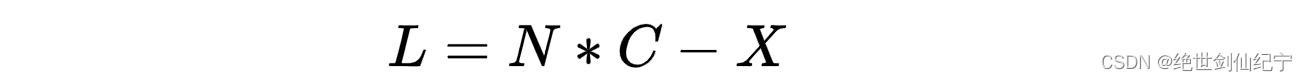
化简得
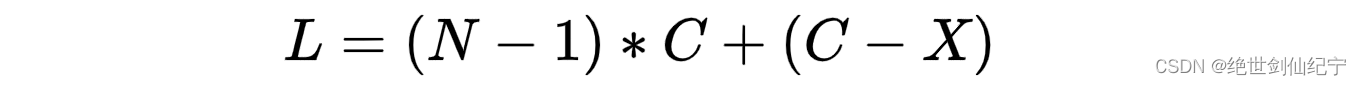 (N-1)*C 为沸羊羊在环里走的整圈的路程,而 (C-X) 为环的长度减去环的入口点到环的相遇点之间的长度。这个公式说明了一件事,当两个速度相同的指针,一个从起点开始走,一个从相遇点开始走,他们一定会在环入口点相遇(可能相遇前一个指针已经绕环很多圈了)。
(N-1)*C 为沸羊羊在环里走的整圈的路程,而 (C-X) 为环的长度减去环的入口点到环的相遇点之间的长度。这个公式说明了一件事,当两个速度相同的指针,一个从起点开始走,一个从相遇点开始走,他们一定会在环入口点相遇(可能相遇前一个指针已经绕环很多圈了)。
源码及思路
首先,要找到快慢指针相遇的点,如果快慢指针没有相遇的话,则说明这个链表没有环。其次,重新定义两个速度相同的指针,一个从快慢指针的相遇点开始绕着环走,一个指针从起点开始走,这两个指针相遇的地方,就是环的入口结点。
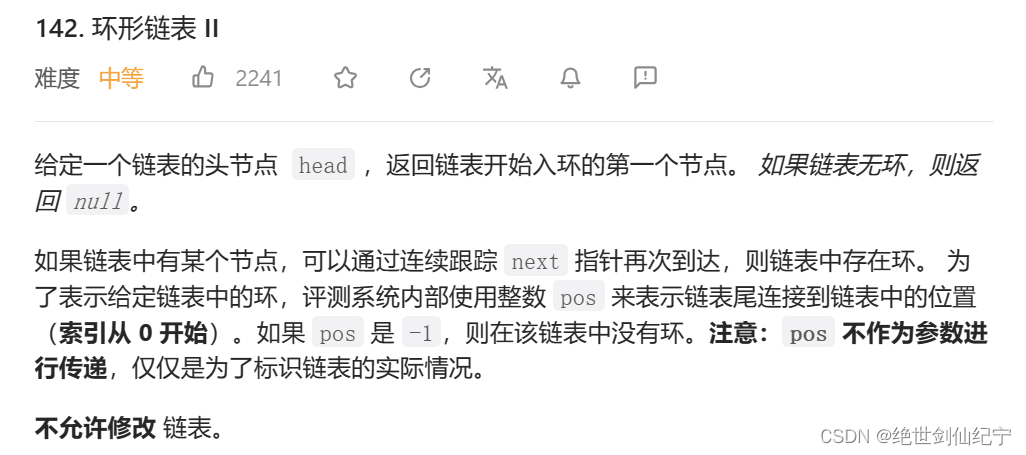
struct ListNode *detectCycle(struct ListNode *head) {struct ListNode *fast=head,*slow=head;while(fast&&fast->next){fast=fast->next->next;slow=slow->next;if(fast==slow)//相遇了{struct ListNode*cur1=head;struct ListNode*cur2=fast;while(cur1!=cur2){cur1=cur1->next;cur2=cur2->next;}return cur1;}}return NULL;
}这是力扣上一道中等难度的题,但是只要分析思路正确了,写代码就是分分钟的问题。
另辟蹊径
第一种思路,在很多人看来,特别是第一次接触这道题的人,比较难理解一点,那这里还有一种思路较为简单的方法,但简单的思路通常伴随着较为复杂的代码,可以说各有取舍吧,大家按需选择。
在此之前,博主在这里再介绍一个经典题目:
判断两个链表是否为相交链表,并找出他们的第一个共同结点
相交链表,即两个链表有重叠的公共结点,他们一旦有公共结点重叠,那么这个结点后面的结点就一定会重合。

判断环形链表的思路是,两个链表各定义一个指针来维护,先遍历计算出链表的长度,顺便比较链表最后一个结点是否重合,如果不重合,则肯定不是相交结点。先让较长链表的指针向前走 差值 步,然后两个指针同时走,直到有一个相同的结点,这个结点就是相交链表的第一个共同结点。
回到刚开始的问题,如何另辟蹊径找到环形链表的入口呢?既然刚才将了相交链表的思路,那肯定一想就直到:转化为相交链表求。
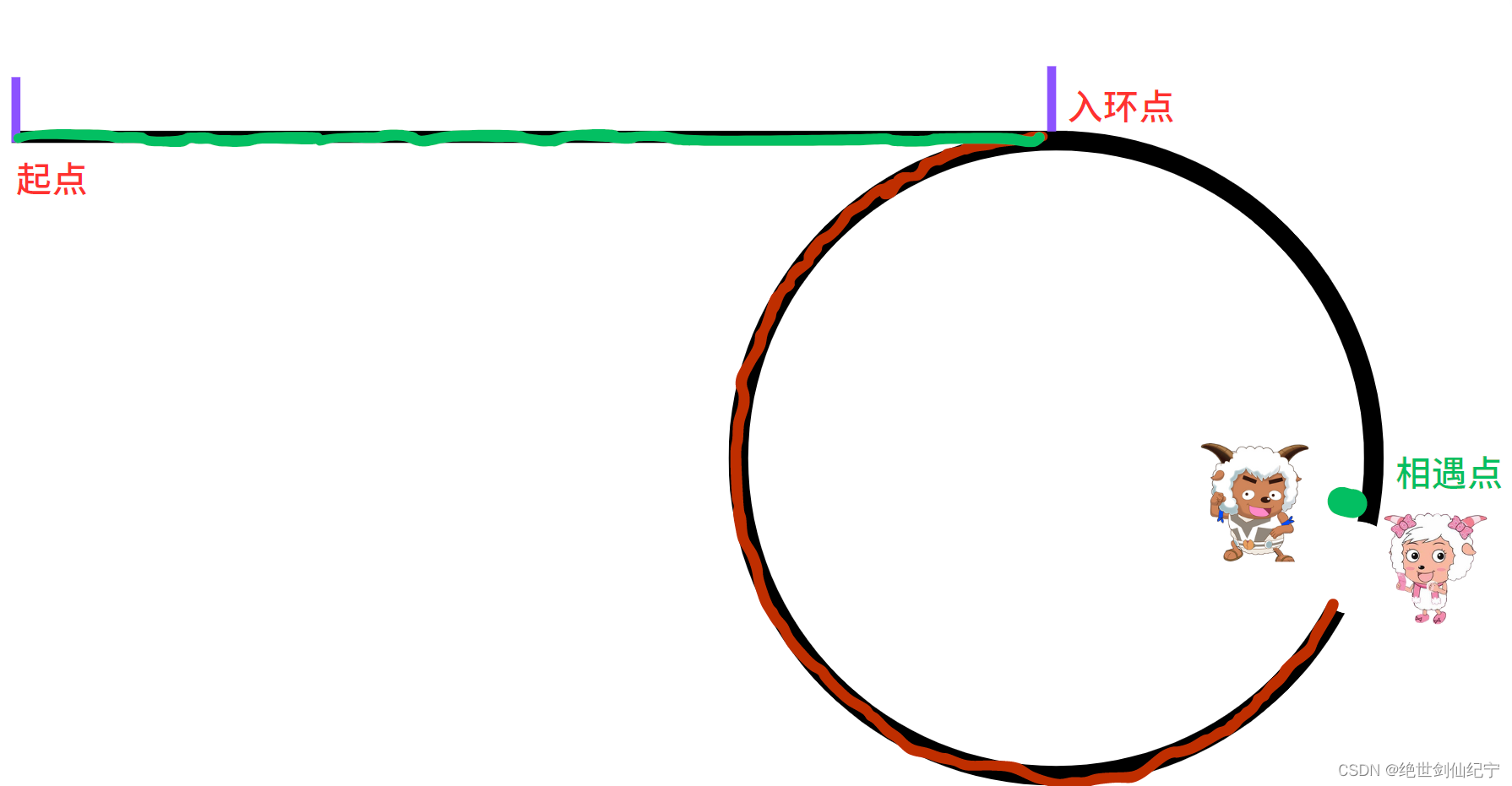
如图,在找到相遇点后,将相遇点断开。红色部分为一个链表,绿色部分为一个链表,他们组成一个相交链表,相交链表的第一个结点就是环形链表的入环结点。
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {int lenA=1,lenB=1;//求相交链表的第一个结点struct ListNode*curA=headA,*curB=headB;while(curA->next!=NULL){curA=curA->next;lenA++;}while(curB->next!=NULL){curB=curB->next;lenB++;}if(curA->val!=curB->val){return NULL;}int dis=abs(lenA-lenB);//求差值绝对值struct ListNode*longnode=headA,*shortnode=headB;if(lenB>lenA){longnode=headB;shortnode=headA;}while(dis--){longnode=longnode->next;}while(longnode!=NULL){if(longnode==shortnode){return longnode;}longnode=longnode->next;shortnode=shortnode->next;}return NULL;
}
struct ListNode *detectCycle(struct ListNode *head) {struct ListNode *slow=head;struct ListNode *fast=head;while(fast&&fast->next){slow=slow->next;fast=fast->next->next;if(fast==slow)//求相遇点{struct ListNode *cur=fast->next;fast->next=NULL;return getIntersectionNode(cur,head);}}return NULL;
}这种方法虽然思路简单,但代码比较长,代码变长,就容易出错,所以说每种方法都是各有利弊。
相关文章:

环形链表的进一步探究
茕茕白兔,东走西顾,衣不如新,人不如故 往期回顾: 数据结构——双向链表 数据结构——单链表 数据结构——顺序表 文章目录 如何判断一个链表是否为环形链表 环形链表的判断的深入探究 例1:沸羊羊追美羊羊 例…...

flink任务性能优化
1、使用异步算子,异步执行操作 2、将下游数据需要的数据以参数的形式向下传递 3、当服务器资源有限的情况下,慎用RocksDBStateBackend RocksDBStateBackend performance will be poor because of the current Flink memory configuration! RocksDB wi…...
vue2 el-carousel轮播图和文字一起改变
vue项目的话 安装一下element依赖 npm i element-ui -S在main入口文件引入element包 我在app文件里边去写的 <template><div class"w"><el-carousel height"460px"><el-carousel-item v-for"item in items" :key"i…...

LangChain:打造自己的LLM应用 | 京东云技术团队
1、LangChain是什么 LangChain是一个框架,用于开发由LLM驱动的应用程序。可以简单认为是LLM领域的Spring,以及开源版的ChatGPT插件系统。核心的2个功能为: 1)可以将 LLM 模型与外部数据源进行连接。 2)允许与 LLM 模…...
字节跳动测试岗,3面都过了,HR告诉我这个原因被刷了...
说在前面 面试时最好不要虚报工资。本来字节跳动是很想去的,几轮面试也通过了,最后没offer,自己只想到下面几个原因: 虚报工资,比实际高30%; 有更好的人选,这个可能性不大,我看还在…...
Android 14重要更新预览
Android 14重要更新预览 国际化 Android 14 在 Android 13 的基础上进一步扩展了按应用设定语言功能,提供了一些额外的功能: 自动生成应用的 localeConfig:从 Android Studio Giraffe Canary 7 和 AGP 8.1.0-alpha07 开始,您可以…...
快速上手字符串函数
文章目录 前言一、求字符串的长度strlen函数strlen函数学习使用strlen函数模拟实现strlen函数模拟实现方法1:计数器法strlen函数模拟实现方法2:指针减指针法strlen函数模拟实现方法3:递归方法 二、字符串的拷贝,拼接和比较strcpy函…...
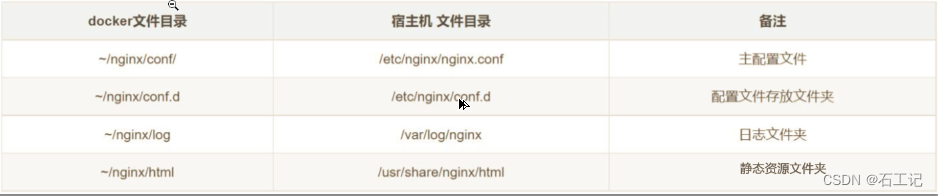
linux(centos) docker 安装 nginx
1、拉取nginx最新版本镜像 docker pull nginx:latest 查看镜像 docker images 或者 docker images -a 2.启动nginx容器 docker run -d -p 80:80 --name nginx nginx 使用docker run命令,启动nginx容器。 --name,设置容器名。为方便记忆ÿ…...

SpringBoot 整合 Minio
官网: MinIO 是一个基于 Go 实现的高性能、兼容 S3 协议的对象存储。它采用 GNU AGPL v3 开源协议,项目地址是 https://github.com/minio/minio 。 它适合存储海量的非结构化的数据,例如说图片、音频、视频等常见文件,备份数据、…...
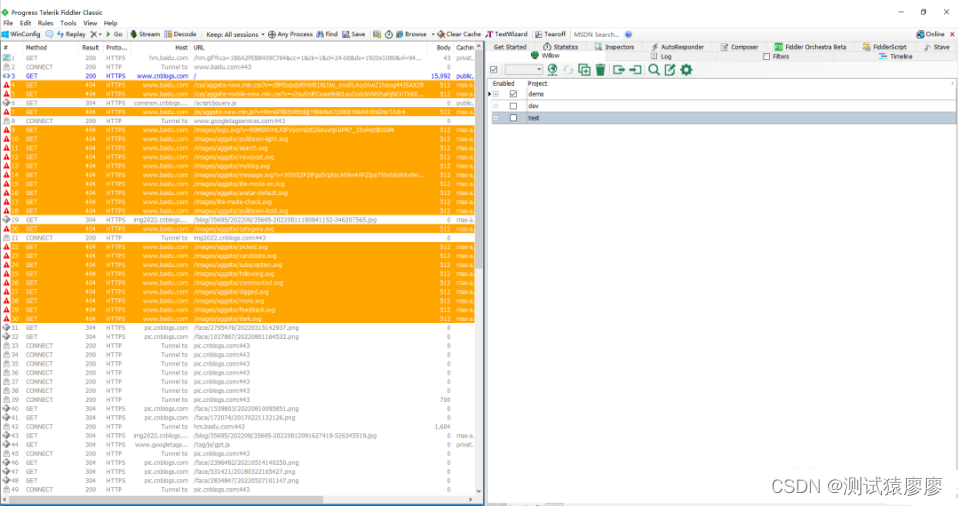
《吐血整理》高级系列教程-吃透Fiddler抓包教程(24)-Fiddler如何优雅地在正式和测试环境之间来回切换-中篇
1.简介 在开发或者测试的过程中,由于项目环境比较多,往往需要来来回回地反复切换,那么如何优雅地切换呢?宏哥今天介绍几种方法供小伙伴或者童鞋们进行参考。 2.实际工作场景 2.1问题场景 (1)已发布线上…...

探索 GPTCache|GPT-4 将开启多模态 AI 时代,GPTCache + Milvus 带来省钱秘籍
世界正处于数字化的浪潮中,为了更好理解和分析大量数据,人们对于人工智能(AI)解决方案的需求呈爆炸式增长。 此前,OpenAI 推出基于 GPT-3.5 模型的智能对话机器人 ChatGPT,在自然语言处理(NLP&a…...

纯css实现登录表单动效
效果图: 代码展示 // 我这边用的是elementUI表单校验,更改的样式。 <el-form:model"form":rules"rules"ref"fromList":hide-required-asterisk"true"><el-form-item prop"account"><…...
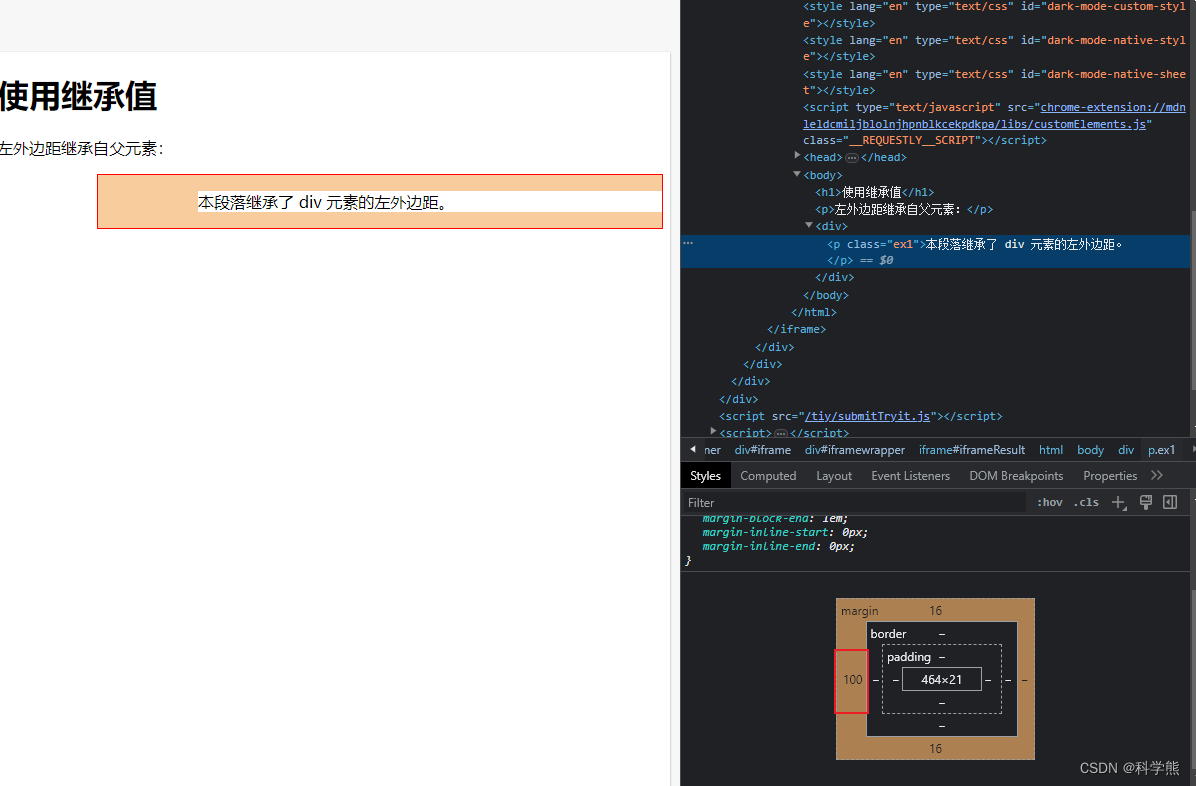
【css】外边距margin
外边距中有一个属性值比较有意思:inherit 值,继承父类的属性。 <!DOCTYPE html> <html> <head> <style> div {border: 1px solid red;margin-left: 100px; }p.ex1 {margin-left: inherit; } </style> </head> <…...

Cpp8 — 二叉搜索树
二叉搜索树(搜索二叉树、二叉排序树) 二叉搜索树又称二叉排序树,它要么是一棵空树,要么是具有以下性质的二叉树: 1.若它的左子树不为空,则左子树上所有节点的值都小于根节点的值 2.若它的右子树不为空&…...
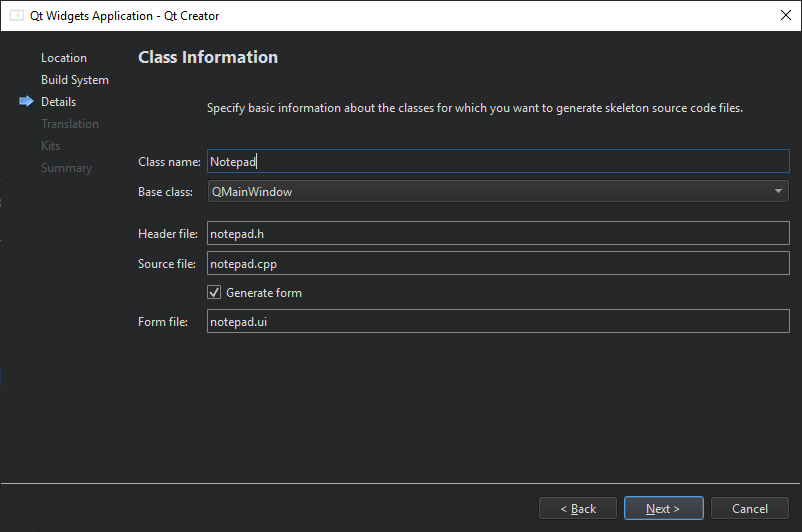
【实操教程】如何开始用Qt Widgets编程?(一)
Qt 是目前最先进、最完整的跨平台C开发工具。它不仅完全实现了一次编写,所有平台无差别运行,更提供了几乎所有开发过程中需要用到的工具。如今,Qt已被运用于超过70个行业、数千家企业,支持数百万设备及应用。 在本文中࿰…...
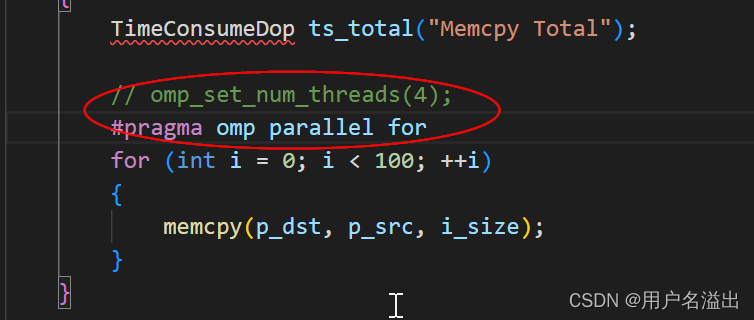
openmp和avx配置
实际场景: 项目中数据拷贝慢(使用的是memcpy),希望能加速拷贝,所以尝试了使用avx的流方式,和openmp方式处理 问题1: 调用avx是报错 error: inlining failed in call to always_inline ‘__m512…...

18 个JS优化技巧,可以解决 90% 的屎山代码!!!
文章目录 18 个JS优化技巧,可以解决 90% 的屎山代码!!!1.箭头函数2.解构赋值变量3.使用模版字面量进行字符拼接4.使用展开运算符进行数组和对象操作5.简化循环6.简化判断7.使用对象解构和默认参数简化函数参数8.使用函数式编程概念…...
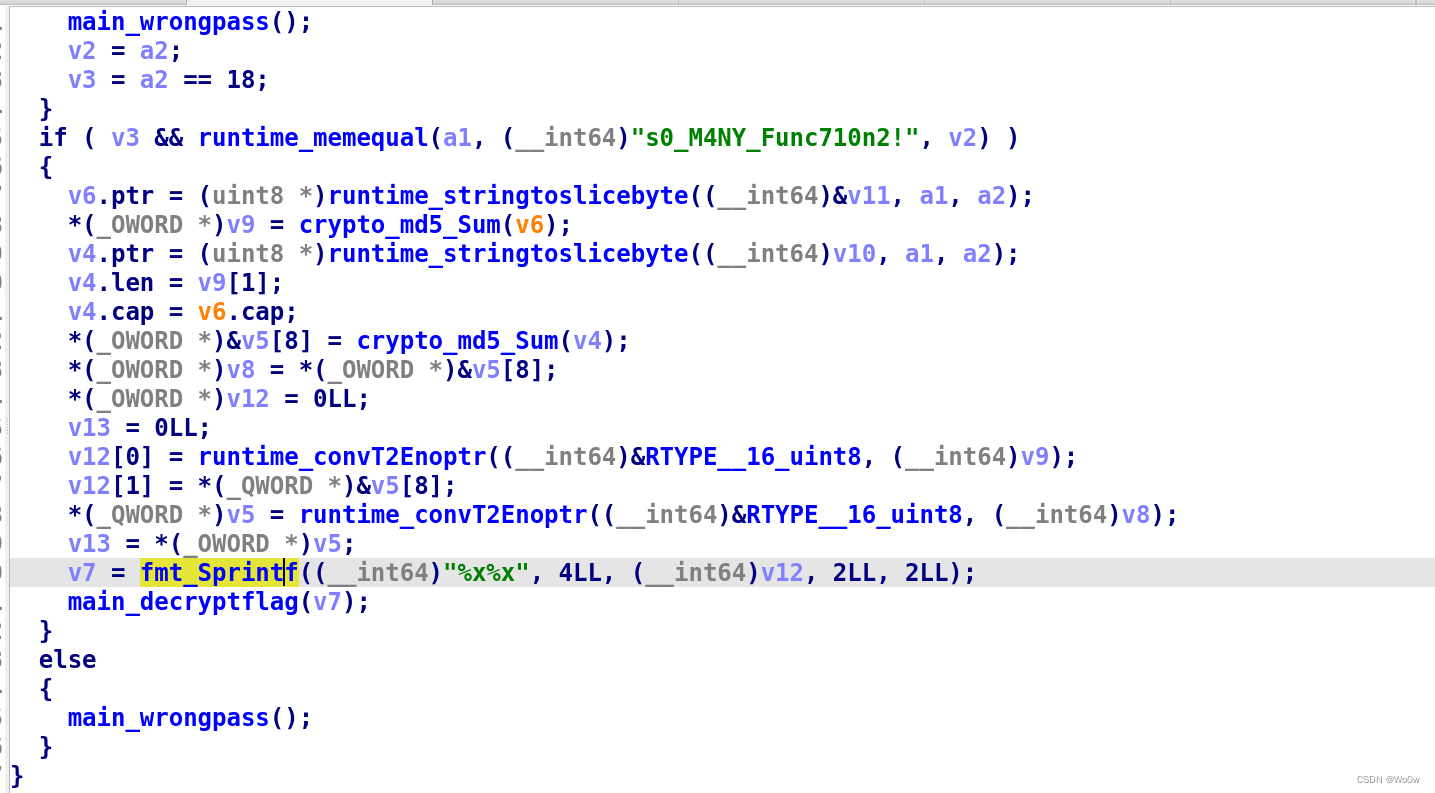
go逆向符号恢复
前言 之前一直没怎么重视,结果发现每次遇到go的题都是一筹莫展,刷几道题练习一下吧 准备 go语言写的程序一般都被strip去掉符号了,而且ida没有相关的签名文件,没办法完成函数名的识别与字符串的定位,所以第一步通常…...
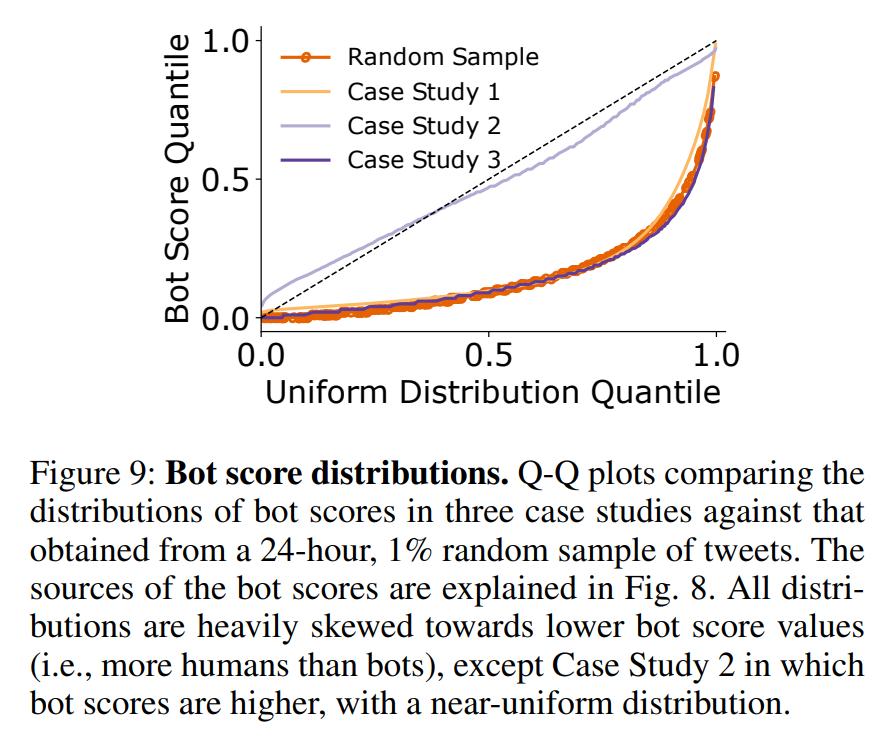
论文阅读- Uncovering Coordinated Networks on Social Media:Methods and Case Studies
链接:https://arxiv.org/pdf/2001.05658.pdf 目录 摘要: 引言 Methods Case Study 1: Account Handle Sharing Coordination Detection 分析 Case Study 2: Image Coordination Coordination Detection Analysis Case Study 3: Hashtag Sequen…...

应急响应-Linux
应急响应-Linux 1.关键目录 /etc/passwd 记录用户信息 /etc/shadow 保存用户密码(hash) /etc/crontab 定时任务文件 /etc/anacrontab 异步定时任务文件 /etc/rc.d/rc.local 开机启动项 /var/log/btmp …...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...

GAN模式奔溃的探讨论文综述(一)
简介 简介:今天带来一篇关于GAN的,对于模式奔溃的一个探讨的一个问题,帮助大家更好的解决训练中遇到的一个难题。 论文题目:An in-depth review and analysis of mode collapse in GAN 期刊:Machine Learning 链接:...
