SPSS数据分析--假设检验的两种原假设取舍决定方式
假设检验的两种原假设取舍决定方式
在t检验,相关分析,回归分析,方差分析,卡方检验等等分析方法中,都需要用到假设检验。假设检验的步骤一般如下:
- 提出假设:H0 vs H1 ;
- 假设原假设H0 成立的情况下,计算一个统计量;
- 在统计分布表中查找临界值,在t检验中,如果确定置信度为 0.05 的话,那么临界值为 t0.05
- 比较临界值和统计量的大小,决定是否接受原假设。如果选择接受原假设,那么原假设 H0 成立;如果选择拒绝原假设,那么备择假设 H1 成立。
通过一张图我们来梳理一下:
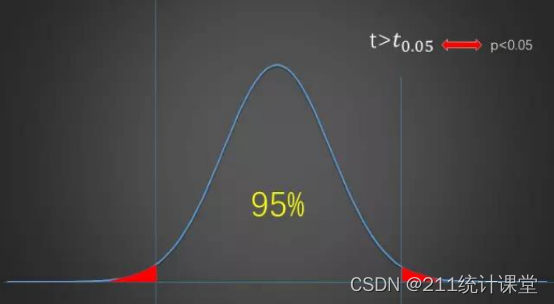
我们先假定原假设是成立的,这样正常情况之下,计算的统计量应该是落在两根线之间的区域的,而如果计算的统计量超出了这个区域,那么说明原假设是有问题的。这里利用了小概率原理:概率很小的事情,在一次试验中,一般不会发生,如果你买过彩票,应该很容易理解这句话。对应于图中就是,红色部分的数值出现的概率很小,出现了就不正常,就要否定原假设,接受备择假设。
现在我们来看,两根线与横轴相交的地方,是一个数值,统计量小于这个数值的绝对值(说绝对值是因为两边都有线),那么统计量就落在中间的 95% 区域中(这个区域也称为接受域),反之则落在外面红色部分的 5% 的区域中。
第一种判断方法就是,用计算的统计量和两个临界值(两根线的位置)比较,如果超出,则拒绝原假设。
第二种方法,如果一个统计量要落在两根线的两边,概率是多少呢,是 0.05,如果再往两边靠呢,那就小于 0.05 了。所以当概率值 p 小于 0.05 时,统计量也超出 95% 的区域了,也要拒绝原假设。
这两种方法本质是一样的,但是一般我们在学校学习计算时,是用前一种方法来判断,而统计软件给出的是第二种判断方法。有的人就不太明白了。本文对该问题的两种不同方式进行了区分,帮助大家认识到其共通之处。
相关文章:

SPSS数据分析--假设检验的两种原假设取舍决定方式
假设检验的两种原假设取舍决定方式 在t检验,相关分析,回归分析,方差分析,卡方检验等等分析方法中,都需要用到假设检验。假设检验的步骤一般如下: 提出假设:H0 vs H1 ;假设原假设H0 成立的情况…...
Python实现猫狗分类
不废话了,直接上代码: def load_imagepath_from_csv(csv_name):image_path []with open(csv_name,r) as file:csv_reader csv.reader(file)next(csv_reader)for row in csv_reader:image_path.append(row[0])return image_pathimport csv csv_name &…...
pjsip、pjsua2+bcg729 windows下编译java版本
文章目录 简要说明流程步骤 简要说明 基本参考的这里 https://docs.pjsip.org/en/latest/get-started/windows/build_instructions.html#building-the-projects 我这里主要是为了生成pjsua2.dll 用于在java下调用。 其中 libbcg729.dll 是通过vcpkg来进行安装。 pjsip使用vs2…...

尝试多数据表 sqlite
C 唯一值得骄傲的地方就是 通过指针来回寻址 😂 提高使用的灵活性 小脚本buff 加成...
Keil出现Flash Timeout.Reset the Target and try it again.我有一种解决方法
2.解决方法 网上查找了找原因,是因为之前代码设置了读保护功能。 读保护即大家通常说的“加密”,是作用于整个Flash存储区域。一旦设置了Flash的读保护,内置的Flash存储区只能通过程序的正常执行才能读出,而不能通过下述任何一种…...

纯粹即刻,畅享音乐搜索的轻松体验
纯粹即刻,畅享音乐搜索的轻松体验 在当今快节奏的生活中,我们常常渴望一种简单而便捷的方式来探索和享受音乐。现在,你可以纯粹即刻地畅享音乐搜索的轻松体验。无论你是寻找热门歌曲还是探索不同风格的音乐,这款应用将为你带来随…...
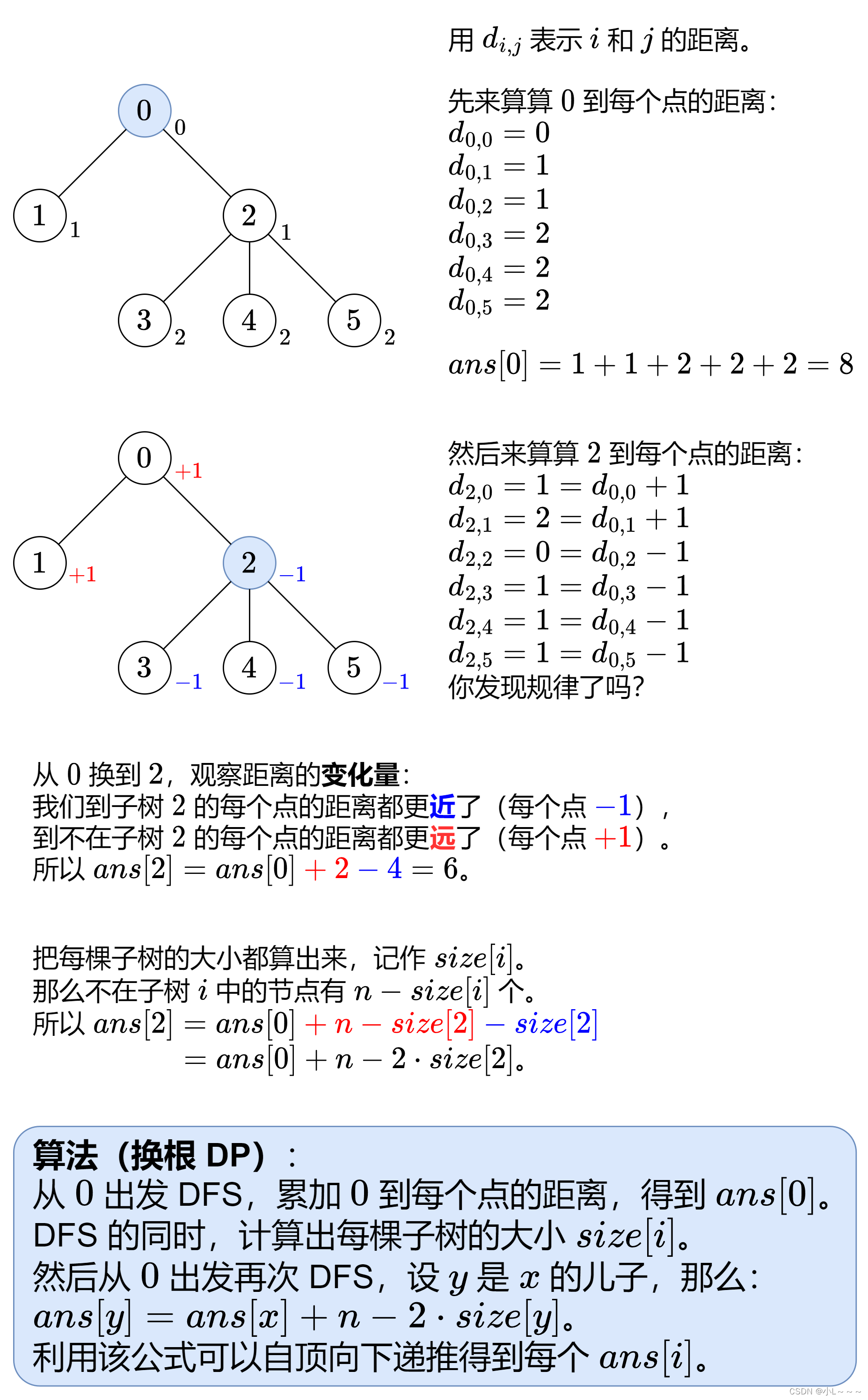
动态规划之树形DP
动态规划之树形DP 树形DP何为树形DP 树形DP例题HDU-1520 Anniversary partyHDU-2196 Computer834. 树中距离之和 树形DP 何为树形DP 树形DP是指在“树”这种数据结构上进行的动态规划:给出一颗树,要求以最少的代价(或取得最大收益ÿ…...

嵌入式_GD32使用宏开关进行Debug串口打印调试
嵌入式_GD32使用宏开关进行Debug串口打印调试 串口Debug是一种将数据通过串口发送的方法。通过使用printf函数,我们可以将需要发送的数据格式化为字符串,并通过串口发送出去。在C语言中,通常使用串口发送数据的函数为printf函数,…...

使用 GitHub Copilot 进行 Prompt Engineering 的初学者指南(译)
文章目录 什么是 GitHub Copilot ?GitHub Copilot 可以自己编码吗?GitHub Copilot 的底层是如何工作的?什么是 prompt engineering?这是 prompt engineering 的另一个例子 使用 GitHub Copilot 进行 prompt engineering 的最佳实践提供高级上下文&…...

c++开发模式,享元模式
享元模式,个人理解,就是应用共享技术来减少类的对象创建,节省计算机资源消耗,而且能够减少维护成本 #include <iostream> #include <string> #include <vector>using namespace std;class Flyweight { public:…...
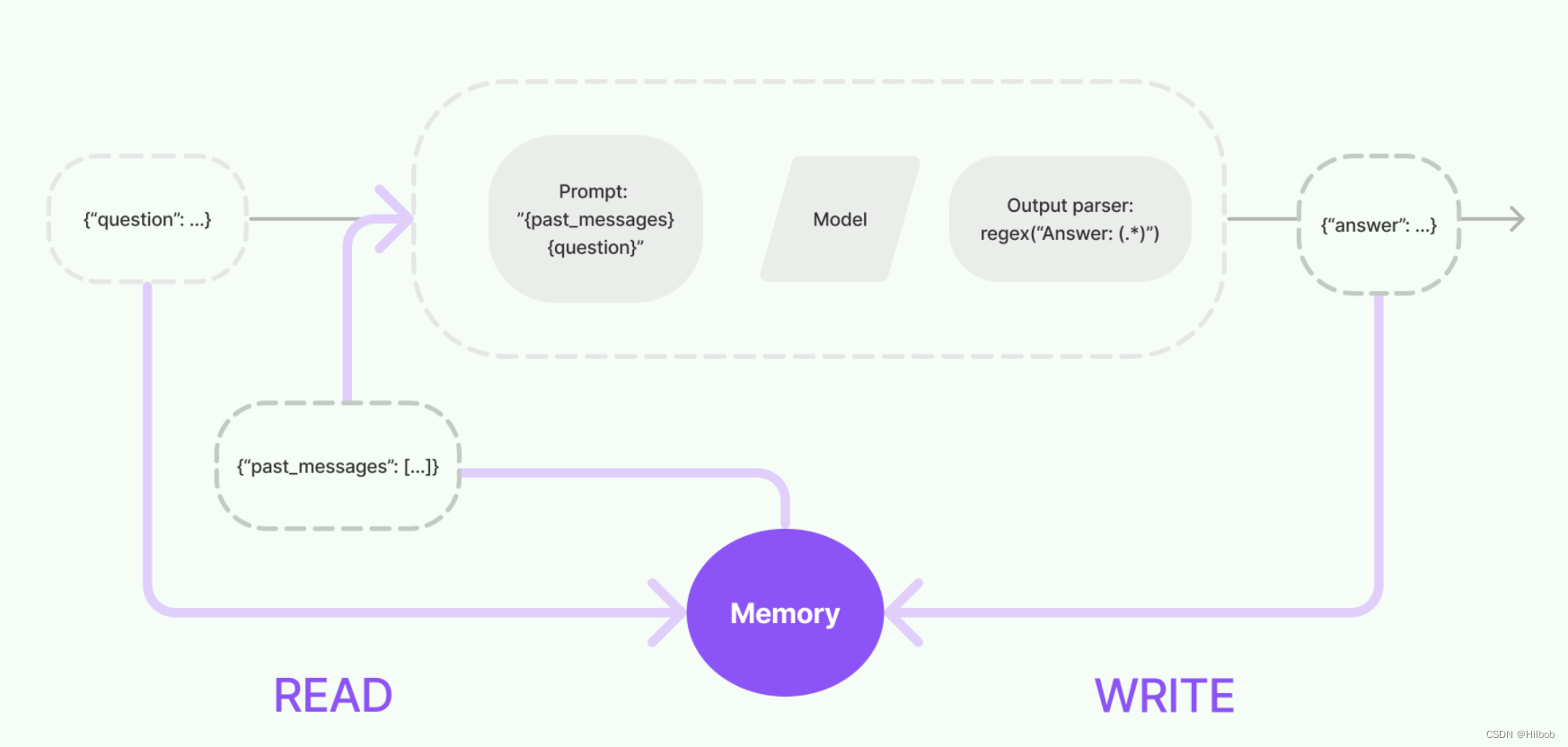
LLM大模型——langchain相关知识总结
目录 一、简介LangChain的主要价值支柱简单安装 二、 LangChain的主要模块1.Model I/Oprompt模版定义调用语言模型 2. 数据连接3. chains4. Agents5. MemoryCallbacks 三、其他记录多进程调用 主要参考以下开源文档 文档地址:https://python.langchain.com/en/lates…...

【Python】数据可视化利器PyCharts在测试工作中的应用
目录 PyCharts 简介 PyCharts 的安装 缺陷统计 测试用例执行情况 使用JavaScript情况 缺陷趋势分析 将两张图放在一个组合里(grid) 将两张图重叠成一张图(overlap) 将多张图组合在一个page 中(page࿰…...
AOP的实战(统一功能处理模块)
一、用户登录权限效验 用户登录权限的发展从之前每个方法中自己验证用户登录权限,到现在统一的用户登录验证处理,它是一个逐渐完善和逐渐优化的过程。 1.1 最初用户登录验证 我们先来回顾一下最初用户登录验证的实现方法: RestController…...

时间复杂度为O(n2)的三种简单排序算法
1.冒泡排序 冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较,看是否满足大小关系要求。如果不满足就让它俩互换。一次冒泡会让至少少一个元素移动到它应该在的位置,重复n次,就完成了n个数据的排序工作。 /*** …...

LeetCode 热题 100 JavaScript --226. 翻转二叉树
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。 示例 3: 输入:root [] 输出:[] 提示: 树中节点数目范围在 [0, 100] 内 -100 < Node.val < 100 var invertTree function(root…...

hive所有窗口函数详情总结
hive窗口函数详情总结 解释语法hive开窗函数排序开窗函数样例数据RANK()DENSE_RANK()ROW_NUMBER() 分析开窗函数样例数据:last_valuefirst_valuelaglead 其他窗口函数cume_distpercent_rank 解释 开窗函数用于为行定义一个窗口(指运算将要操作的行的集合…...

Talk | 新加坡国立大学博士生施宇钧:DragDiffusion-基于扩散模型的关键点拖拽图片编辑
本期为TechBeat人工智能社区第518期线上Talk! 北京时间8月2日(周三)20:00, 新加坡国立大学博士生—施宇钧的Talk已准时在TechBeat人工智能社区开播! 他与大家分享的主题是: “DragDiffusion-基于扩散模型的关键点拖拽图片编辑”,他…...

22 | 贝叶斯分类算法
文章目录 介绍什么是贝叶斯分类算法?贝叶斯分类算法的应用场景贝叶斯定理贝叶斯定理的基本原理贝叶斯定理的公式推导贝叶斯定理的应用举例代码介绍 什么是贝叶斯分类算法? 贝叶斯分类算法是一类基于贝叶斯定理的分类技术。在统计分类任务中,这些算法使用特定的假设来建立特…...

java.sql.SQLSyntaxErrorException: ORA-00909: 参数个数无效
问题: 在Select里采用Contact(%,#name,%)报错参数个数无效 原因: 回想以前用Mysql的时候就是这样用的,没有问题,在这里就出问题了,所以确定问题在oracle数据库上,经过查询得知,oracle和mysql…...

数据结构8-哈希表
数据结构8-哈希表 动态分配内存方式: #include <stdio.h> #include <stdlib.h>#define SIZE 20struct DataItem {int data; int key; };struct DataItem* hashArray[SIZE]; struct DataItem* dummyItem; struct DataItem* item;//获取键值 int has…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...

Neko虚拟浏览器远程协作方案:Docker+内网穿透技术部署实践
前言:本文将向开发者介绍一款创新性协作工具——Neko虚拟浏览器。在数字化协作场景中,跨地域的团队常需面对实时共享屏幕、协同编辑文档等需求。通过本指南,你将掌握在Ubuntu系统中使用容器化技术部署该工具的具体方案,并结合内网…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...

Redis上篇--知识点总结
Redis上篇–解析 本文大部分知识整理自网上,在正文结束后都会附上参考地址。如果想要深入或者详细学习可以通过文末链接跳转学习。 1. 基本介绍 Redis 是一个开源的、高性能的 内存键值数据库,Redis 的键值对中的 key 就是字符串对象,而 val…...

Netty自定义协议解析
目录 自定义协议设计 实现消息解码器 实现消息编码器 自定义消息对象 配置ChannelPipeline Netty提供了强大的编解码器抽象基类,这些基类能够帮助开发者快速实现自定义协议的解析。 自定义协议设计 在实现自定义协议解析之前,需要明确协议的具体格式。例如,一个简单的…...
