Stephen Wolfram:神经网络
Neural Nets
神经网络
OK, so how do our typical models for tasks like image recognition actually work? The most popular—and successful—current approach uses neural nets. Invented—in a form remarkably close to their use today—in the 1940s, neural nets can be thought of as simple idealizations of how brains seem to work.
好的,那么我们对于图像识别等典型任务的模型实际上是如何工作的呢?目前最流行且最成功的方法是使用神经网络。神经网络在 20 世纪 40 年代发明,其形式与现在的使用非常接近,可以被看作是对大脑工作原理的简单理想化。
In human brains there are about 100 billion neurons (nerve cells), each capable of producing an electrical pulse up to perhaps a thousand times a second. The neurons are connected in a complicated net, with each neuron having tree-like branches allowing it to pass electrical signals to perhaps thousands of other neurons. And in a rough approximation, whether any given neuron produces an electrical pulse at a given moment depends on what pulses it’s received from other neurons—with different connections contributing with different “weights”.
人类大脑中有约 1000 亿个神经元(神经细胞),每个神经元每秒可以产生电脉冲多达数千次。神经元通过复杂的网络连接在一起,每个神经元都有类似树枝的分支,使其能够将电信号传递给数千个其他神经元。在粗略的近似下,任何给定神经元在给定时刻是否产生电脉冲取决于其从其他神经元接收到的脉冲,不同的连接以不同的“权重”进行贡献。
When we “see an image” what’s happening is that when photons of light from the image fall on (“photoreceptor”) cells at the back of our eyes they produce electrical signals in nerve cells. These nerve cells are connected to other nerve cells, and eventually the signals go through a whole sequence of layers of neurons. And it’s in this process that we “recognize” the image, eventually “forming the thought” that we’re “seeing a 2” (and maybe in the end doing something like saying the word “two” out loud).
当我们“看到一张图像”时,光子从图像上落在我们眼睛背后的“光感受器”细胞上,它们会在神经元中产生电信号。这些神经元与其他神经元相连,信号经过一系列层的神经元。在这个过程中,我们“识别”图像,最终“形成思维”,认为我们“看到了一个 2”(最后可能会做出说出“2”这样的动作)。
The “black-box” function from the previous section is a “mathematicized” version of such a neural net. It happens to have 11 layers (though only 4 “core layers”):
前面部分的“黑盒子”函数是这样一个“数学化”的神经网络版本。它有 11 层(但只有 4 个“核心层”):

There’s nothing particularly “theoretically derived” about this neural net; it’s just something that—back in 1998—was constructed as a piece of engineering, and found to work. (Of course, that’s not much different from how we might describe our brains as having been produced through the process of biological evolution.)
这个神经网络并没有什么特别“理论上的推导”;它只是在 1998 年构建为一项工程,并被发现有效。(当然,这与我们可能描述人类大脑是如何通过生物进化过程产生的方式并没有太大区别。)
OK, but how does a neural net like this “recognize things”? The key is the notion of attractors. Imagine we’ve got handwritten images of 1’s and 2’s:
那么,像这样的神经网络是如何“识别事物”的呢?关键在于吸引子的概念。假设我们有手写的 1 和 2 的图像:

We somehow want all the 1’s to “be attracted to one place”, and all the 2’s to “be attracted to another place”. Or, put a different way, if an image is somehow “closer to being a 1” than to being a 2, we want it to end up in the “1 place” and vice versa.
我们希望所有的 1 都能“被吸引到一个地方”,而所有的 2 都能“被吸引到另一个地方”。换句话说,如果一个图像在某种程度上“更接近 1”而不是 2,我们希望它最终位于“1 的地方”,反之亦然。
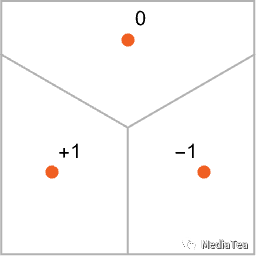
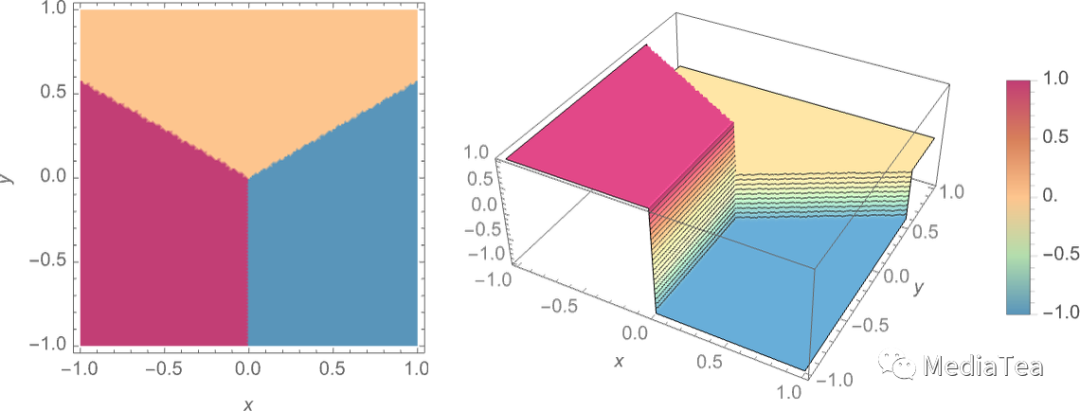
As a straightforward analogy, let’s say we have certain positions in the plane, indicated by dots (in a real-life setting they might be positions of coffee shops). Then we might imagine that starting from any point on the plane we’d always want to end up at the closest dot (i.e. we’d always go to the closest coffee shop). We can represent this by dividing the plane into regions (“attractor basins”) separated by idealized “watersheds”:
作为一个直观的类比,我们假设平面上有一些位置,由点(在现实生活中它们可能是咖啡店的位置)表示。然后我们可以想象,从平面上的任意一点出发,我们总是希望最终到达最近的点(也就是我们总是去最近的咖啡店)。我们可以通过将平面划分为由理想化的“分水岭”分隔的区域(“吸引子盆地”)来表示这一点:

We can think of this as implementing a kind of “recognition task” in which we’re not doing something like identifying what digit a given image “looks most like”—but rather we’re just, quite directly, seeing what dot a given point is closest to. (The “Voronoi diagram” setup we’re showing here separates points in 2D Euclidean space; the digit recognition task can be thought of as doing something very similar—but in a 784-dimensional space formed from the gray levels of all the pixels in each image.)
我们可以将此视为实现“识别任务”的一种方式,我们并不是在做类似于确定给定图像“看起来最像哪个数字”的事情,而是直接看给定点最接近的是哪个点。(我们在这里展示的“沃罗诺伊图”设置将 2D 欧氏空间中的点分隔开;数字识别任务可以认为是在 784 维空间中进行,该空间由每个图像中所有像素的灰度级组成。)
So how do we make a neural net “do a recognition task”? Let’s consider this very simple case:
那么,我们如何使神经网络“执行识别任务”呢?让我们考虑这个非常简单的例子:
Our goal is to take an “input” corresponding to a position {x,y}—and then to “recognize” it as whichever of the three points it’s closest to. Or, in other words, we want the neural net to compute a function of {x,y} like:
我们的目标是将“输入”转换为对应于位置{x,y}的点,并将其“识别”为最接近的三个点之一。换句话说,我们希望神经网络计算关于{x,y}的函数,如下所示:
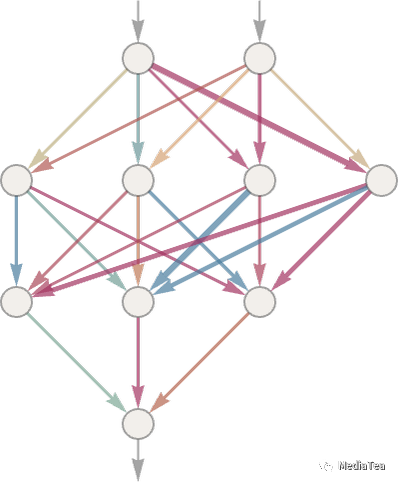
So how do we do this with a neural net? Ultimately a neural net is a connected collection of idealized “neurons”—usually arranged in layers—with a simple example being:
那么我们如何用神经网络实现这个呢?从根本上讲,神经网络是由一系列理想化的“神经元”相互连接而成的,通常按层排列,一个简单的例子是:
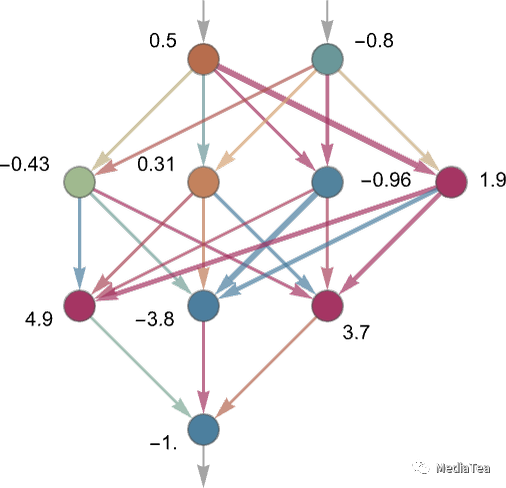
Each “neuron” is effectively set up to evaluate a simple numerical function. And to “use” the network, we simply feed numbers (like our coordinates x and y) in at the top, then have neurons on each layer “evaluate their functions” and feed the results forward through the network—eventually producing the final result at the bottom:
每个“神经元”实际上被设置为评估一个简单的数值函数。为了“使用”网络,我们只需在顶部输入数字(例如我们的坐标 x 和 y),然后在每个层上的神经元“评估它们的函数”并将结果通过网络向前传递——最终在底部产生最终结果:
In the traditional (biologically inspired) setup each neuron effectively has a certain set of “incoming connections” from the neurons on the previous layer, with each connection being assigned a certain “weight” (which can be a positive or negative number). The value of a given neuron is determined by multiplying the values of “previous neurons” by their corresponding weights, then adding these up and adding a constant—and finally applying a “thresholding” (or “activation”) function. In mathematical terms, if a neuron has inputs x = {x1, x2 …} then we compute f[w . x + b], where the weights w and constant b are generally chosen differently for each neuron in the network; the function f is usually the same.
在传统的(生物启发式的)设置中,每个神经元实际上都有来自上一层神经元的一组“输入连接”,每个连接都被赋予某个“权重”(可以是正数或负数)。给定神经元的值是通过将“上一层神经元”的值与它们对应的权重相乘,然后相加并加上一个常数——最后应用一个“阈值”(或“激活”)函数来确定的。在数学上,如果一个神经元具有输入 x = {x1,x2...},那么我们计算 f[w·x + b],其中权重 w 和常数 b 通常对于网络中的每个神经元选择不同;函数 f 通常是相同的。
Computing w . x + b is just a matter of matrix multiplication and addition. The “activation function” f introduces nonlinearity (and ultimately is what leads to nontrivial behavior). Various activation functions commonly get used; here we’ll just use Ramp (or ReLU):
计算 w·x + b 只是矩阵乘法和加法的问题。激活函数 f 引入了非线性(最终导致不平凡的行为)。通常会使用不同的激活函数;在这里,我们使用了 Ramp(或 ReLU):

For each task we want the neural net to perform (or, equivalently, for each overall function we want it to evaluate) we’ll have different choices of weights. (And—as we’ll discuss later—these weights are normally determined by “training” the neural net using machine learning from examples of the outputs we want.)
对于我们希望神经网络执行的每个任务(或等效地,我们希望它评估的每个整体函数),我们都有不同的权重选择。(我们稍后将讨论这些权重通常是通过使用机器学习来从我们希望的输出的示例中“训练”神经网络得到的。)
Ultimately, every neural net just corresponds to some overall mathematical function—though it may be messy to write out. For the example above, it would be:
归根结底,每个神经网络只对应于某个整体数学函数——尽管可能很难写出。对于上面的例子,它将是:
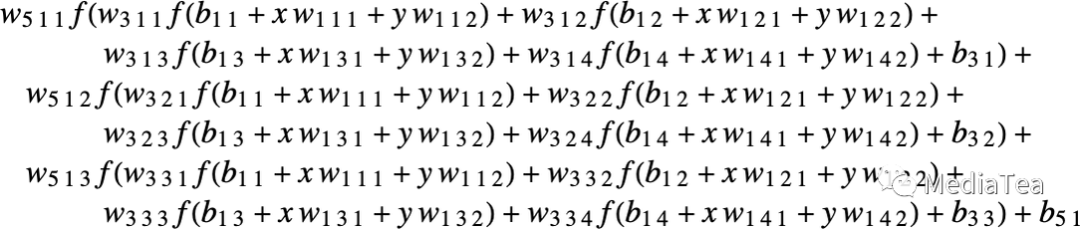
The neural net of ChatGPT also just corresponds to a mathematical function like this—but effectively with billions of terms.
ChatGPT 的神经网络也只是对应于这样一个数学函数——但是有效地有数十亿个项。
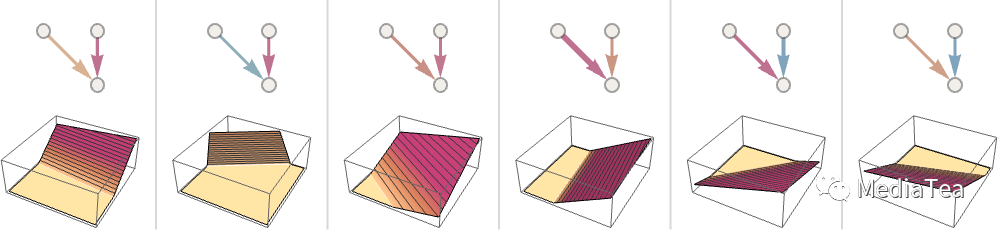
But let’s go back to individual neurons. Here are some examples of the functions a neuron with two inputs (representing coordinates x and y) can compute with various choices of weights and constants (and Ramp as activation function):
不过让我们回到单个神经元。以下是一个具有两个输入(表示坐标 x 和 y)的神经元根据不同的权重和常数(以及 Ramp 作为激活函数)所计算的一些函数示例:
But what about the larger network from above? Well, here’s what it computes:
那么上面的较大网络呢?好吧,它计算的是这个:
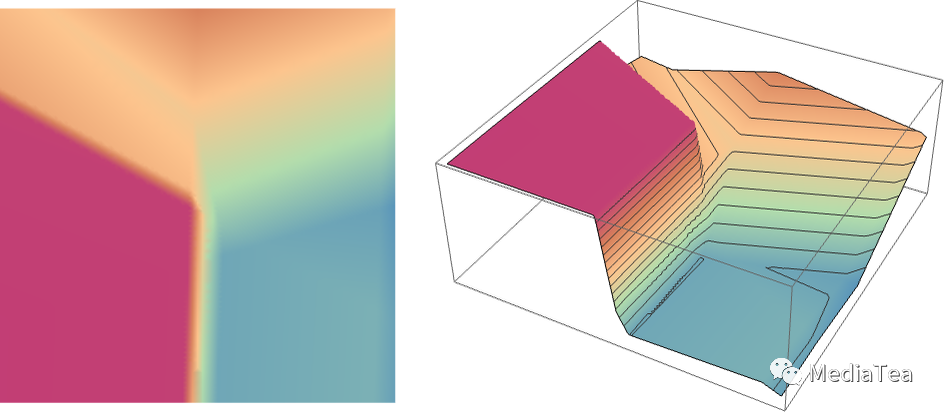
It’s not quite “right”, but it’s close to the “nearest point” function we showed above.
这并不完全“正确”,但它接近我们之前展示的“最近点”函数。
Let’s see what happens with some other neural nets. In each case, as we’ll explain later, we’re using machine learning to find the best choice of weights. Then we’re showing here what the neural net with those weights computes:
让我们看看其他神经网络发生了什么。在每种情况下,正如我们稍后将解释的,我们都在使用机器学习来找到最佳的权重选择。然后我们在这里展示这些权重的神经网络计算的结果:
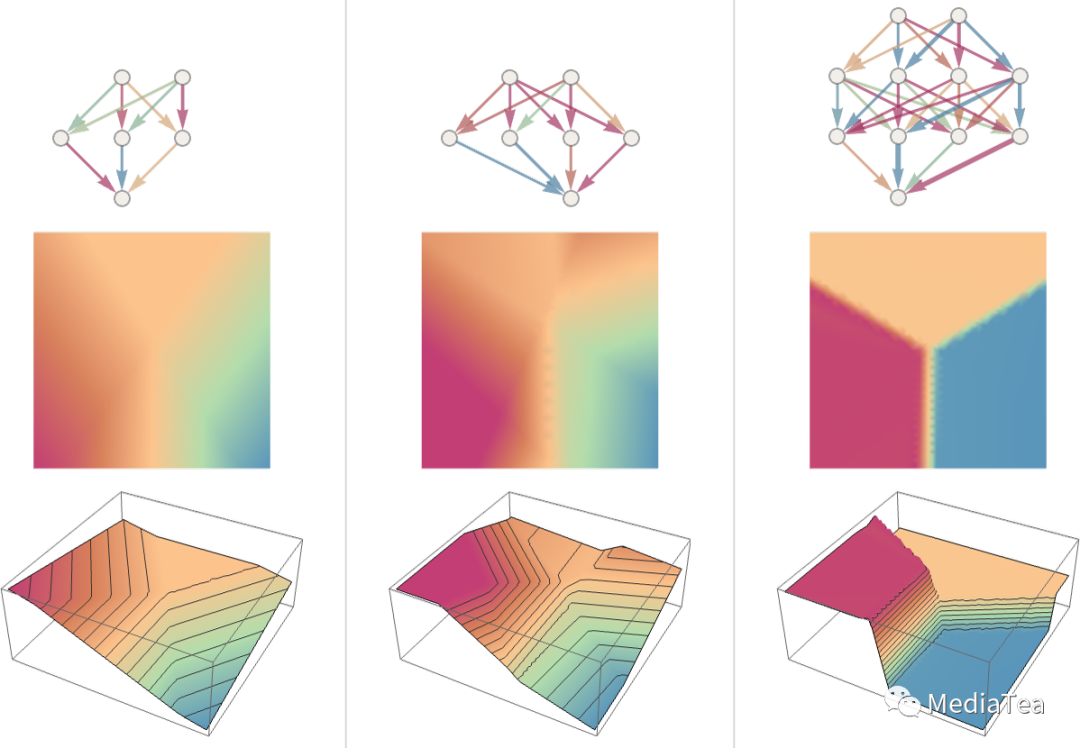
Bigger networks generally do better at approximating the function we’re aiming for. And in the “middle of each attractor basin” we typically get exactly the answer we want. But at the boundaries—where the neural net “has a hard time making up its mind”—things can be messier.
更大的网络通常在逼近我们目标函数方面做得更好。在各个“吸引子盆地”的中部,我们通常可以得到我们想要的确切答案。但在边界处——神经网络“很难做出决定”的地方——事情可能会更混乱。
With this simple mathematical-style “recognition task” it’s clear what the “right answer” is. But in the problem of recognizing handwritten digits, it’s not so clear. What if someone wrote a “2” so badly it looked like a “7”, etc.? Still, we can ask how a neural net distinguishes digits—and this gives an indication:
在这个简单的数学风格的“识别任务”中,很明显是什么是“正确答案”。但在识别手写数字的问题中,情况并不那么明确。如果有人把“2”写得很糟糕,看起来像“7”之类的数字,怎么办?尽管如此,我们可以问神经网络如何区分数字,这会给出一个指示:

Can we say “mathematically” how the network makes its distinctions? Not really. It’s just “doing what the neural net does”. But it turns out that that normally seems to agree fairly well with the distinctions we humans make.
我们能否以“数学”的方式描述神经网络是如何进行区分的呢?其实不能。它只是在“做神经网络该做的事”。但结果表明,这通常与我们人类所做的区分相当一致。
Let’s take a more elaborate example. Let’s say we have images of cats and dogs. And we have a neural net that’s been trained to distinguish them. Here’s what it might do on some examples:
让我们看一个更复杂的例子。假设我们有猫和狗的图片,还有一个经过训练的神经网络,用于区分它们。在一些例子中,它可能会这么做:

Now it’s even less clear what the “right answer” is. What about a dog dressed in a cat suit? Etc. Whatever input it’s given the neural net will generate an answer, and in a way reasonably consistent with how humans might. As I’ve said above, that’s not a fact we can “derive from first principles”. It’s just something that’s empirically been found to be true, at least in certain domains. But it’s a key reason why neural nets are useful: that they somehow capture a “human-like” way of doing things.
现在“正确答案”变得更加不清楚。如果有一只穿着猫装的狗呢?等等。无论输入是什么,神经网络都会生成一个答案,并以与人类相当一致的方式。就像我前面所说的,这并不是一个我们可以“从第一原则推导出来”的事实。这只是一些经验性的发现,至少在某些领域是成立的。但这是为什么神经网络是有用的关键原因:它们以某种方式捕捉了“类似于人类”的处理方式。
Show yourself a picture of a cat, and ask “Why is that a cat?”. Maybe you’d start saying “Well, I see its pointy ears, etc.” But it’s not very easy to explain how you recognized the image as a cat. It’s just that somehow your brain figured that out. But for a brain there’s no way (at least yet) to “go inside” and see how it figured it out. What about for an (artificial) neural net? Well, it’s straightforward to see what each “neuron” does when you show a picture of a cat. But even to get a basic visualization is usually very difficult.
向自己展示一张猫的图片,然后问:“为什么这是一只猫?”或许你会开始说:“嗯,我看到它尖尖的耳朵等等。”但解释你如何识别出这是一张猫的图片并不容易。只是不知怎么的,你的大脑就搞定了。但对于大脑来说,目前(至少)没有办法“进入”并看看它是如何弄清楚的。那么对于(人造的)神经网络呢?嗯,很难将其可视化。
In the final net that we used for the “nearest point” problem above there are 17 neurons. In the net for recognizing handwritten digits there are 2190. And in the net we’re using to recognize cats and dogs there are 60,650. Normally it would be pretty difficult to visualize what amounts to 60,650-dimensional space. But because this is a network set up to deal with images, many of its layers of neurons are organized into arrays, like the arrays of pixels it’s looking at.
在我们上面使用的最终网络中,有 17 个神经元。在用于识别手写数字的网络中,有 2190 个神经元。在我们用于识别猫和狗的网络中,有 60650 个神经元。通常,对于一个拥有 60650 维度的空间,将其可视化是非常困难的。但由于这是一个处理图像的网络,它的许多神经元层都组织成类似于它正在查看的像素阵列。
And if we take a typical cat image,
如果我们拿一个典型的猫的图片

then we can represent the states of neurons at the first layer by a collection of derived images—many of which we can readily interpret as being things like “the cat without its background”, or “the outline of the cat”:
然后我们可以通过一系列衍生图片来表示第一层的神经元的状态,其中很多图片我们可以轻松解释为“没有背景的猫”,或者“猫的轮廓”等:

By the 10th layer it’s harder to interpret what’s going on:
到第 10 层,很难解释正在发生什么:

But in general we might say that the neural net is “picking out certain features” (maybe pointy ears are among them), and using these to determine what the image is of. But are those features ones for which we have names—like “pointy ears”? Mostly not.
但总的来说,我们可以说神经网络“挑选出某些特征”,然后使用这些特征来确定图像所代表的是什么。但这些特征是否与我们有名称的特征相似,比如“尖尖的耳朵”?大多数并不是。
Are our brains using similar features? Mostly we don’t know. But it’s notable that the first few layers of a neural net like the one we’re showing here seem to pick out aspects of images (like edges of objects) that seem to be similar to ones we know are picked out by the first level of visual processing in brains.
我们的大脑是否使用类似的特征?我们大多数情况下并不知道。但值得注意的是,我们在这里展示的网络的前几层似乎会提取出与大脑中视觉处理的第一层所提取的相似的图像特征(如物体边缘)。
But let’s say we want a “theory of cat recognition” in neural nets. We can say: “Look, this particular net does it”—and immediately that gives us some sense of “how hard a problem” it is (and, for example, how many neurons or layers might be needed). But at least as of now we don’t have a way to “give a narrative description” of what the network is doing. And maybe that’s because it truly is computationally irreducible, and there’s no general way to find what it does except by explicitly tracing each step. Or maybe it’s just that we haven’t “figured out the science”, and identified the “natural laws” that allow us to summarize what’s going on.
但是,假设我们想要一个神经网络中的“猫识别理论”。我们可以说:“看,这个特定的网络能做到这一点”——这立刻让我们对“问题有多难”有了一定的了解(例如,可能需要多少神经元或层数)。但至少到目前为止,我们还没有办法“用叙述性的方式描述”网络在做什么。也许这是因为它在计算上是不可化简的,除非我们显式地追踪每一步。或者也许是因为我们还没有“解释这个科学”,找到了允许我们总结发生的事情的“自然法则”。
We’ll encounter the same kinds of issues when we talk about generating language with ChatGPT. And again it’s not clear whether there are ways to “summarize what it’s doing”. But the richness and detail of language (and our experience with it) may allow us to get further than with images.
当我们讨论使用 ChatGPT 生成语言时,我们将遇到相同类型的问题。同样,目前还不清楚是否有办法“总结它在做什么”。但是语言的丰富性和细节(以及我们对它的经验)可能使我们在这方面取得更大的进展。

“点赞有美意,赞赏是鼓励”
相关文章:

Stephen Wolfram:神经网络
Neural Nets 神经网络 OK, so how do our typical models for tasks like image recognition actually work? The most popular—and successful—current approach uses neural nets. Invented—in a form remarkably close to their use today—in the 1940s, neural nets …...
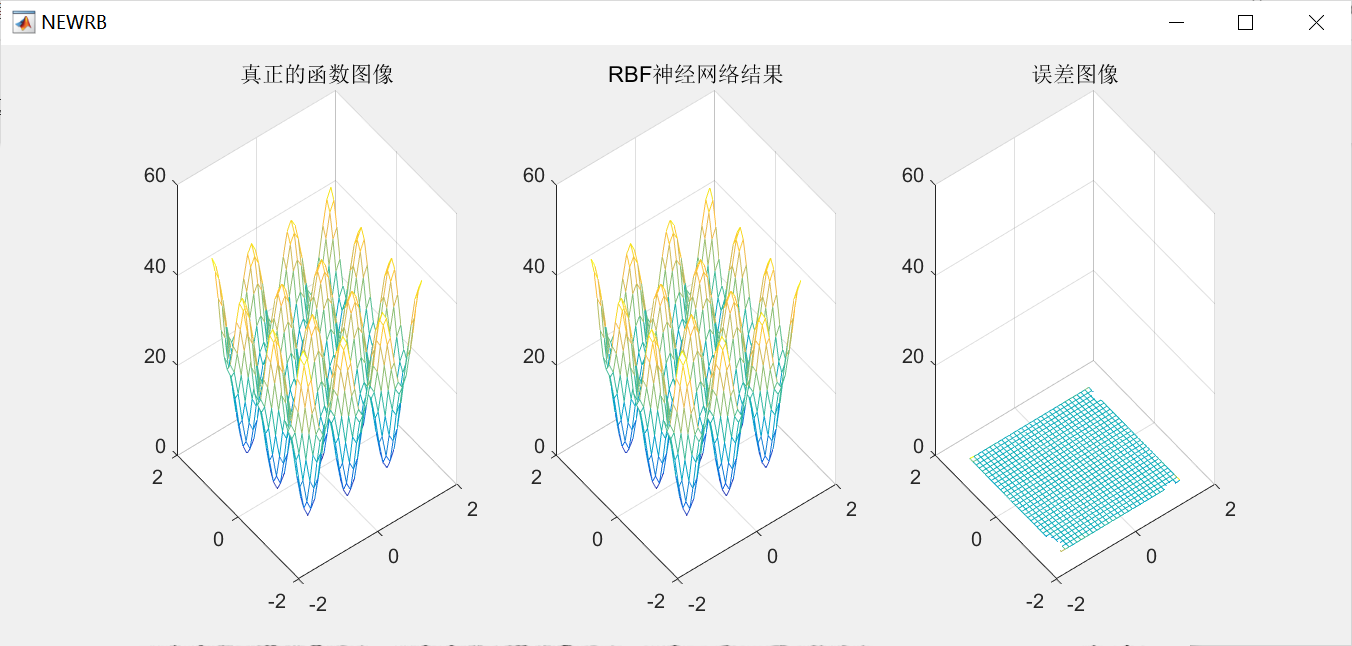
RBF神经网络原理和matlab实现
1.案例背景 1.1 RBF神经网络概述 径向基函数(Radical Basis Function,RBF)是多维空间插值的传统技术,由Powell于1985年提出。1988年, Broomhead和 Lowe根据生物神经元具有局部响应这一特点,将 RBF引入神经网络设计中,产生了RBF神经网络。1989 年,Jackson论证了…...
Nacos 抽取公共配置
文章目录 创建一个公共配置文件其他配置文件引用springboot配置文件 创建一个公共配置文件 其他配置文件引用 ${变量} springboot配置文件 spring:cloud:nacos:discovery:server-addr: current.ip:8848namespace: word_register_proconfig:server-addr: current.ip:8848auto-r…...

Promise、Async/Await 详解
一、什么是Promise Promise是抽象异步处理对象以及对其进行各种操作的组件。Promise本身是同步的立即执行函数解决异步回调的问题, 当调用 resolve 或 reject 回调函数进行处理的时候, 是异步操作, 会先执行.then/catch等,当主栈完成后&#…...

PoseiSwap:基于 Nautilus Chain ,构建全新价值体系
在 DeFi Summer 后,以太坊自身的弊端不断凸显,而以 Layer2 的方式为其扩容成为了行业很长一段时间的叙事方向之一。虽然以太坊已经顺利的从 PoW 的 1.0 迈向了 PoS 的 2.0 时代,但以太坊创始人 Vitalik Buterin 表示, Layer2 未来…...

uC-OS2 V2.93 STM32L476 移植:串口打印篇
前言 前几篇已经 通过 STM32CubeMX 搭建了 NUCLEO-L476RG 的 STM32L476RG 的 裸机工程,下载了 uC-OS2 V2.93 的源码,并把 uC-OS2 的源文件加入 Keil MDK5 工程,通过适配 Systick 系统定时器与 PendSV 实现任务调度,初步让 uC-OS2 …...

代码随想录算法训练营第四十六天| 139.单词拆分 背包问题总结
代码随想录算法训练营第四十六天| 139.单词拆分 背包问题总结 一、力扣139.单词拆分 题目链接: 思路:确定dp数组,dp[i]为true表示从0到i切分的字串都在字典中出现过。 确定递推公式,dp[i] 为true要求 s[j, i] 在字典中出现&…...
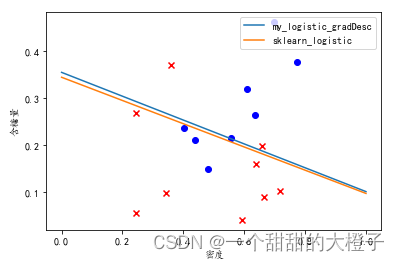
【机器学习】西瓜书习题3.3Python编程实现对数几率回归
参考代码 结合自己的理解,添加注释。 代码 导入相关的库 import numpy as np import pandas as pd import matplotlib from matplotlib import pyplot as plt from sklearn import linear_model导入数据,进行数据处理和特征工程 # 1.数据处理&#x…...
Blazor前后端框架Known-V1.2.9
V1.2.9 Known是基于C#和Blazor开发的前后端分离快速开发框架,开箱即用,跨平台,一处代码,多处运行。 Gitee: https://gitee.com/known/KnownGithub:https://github.com/known/Known 概述 基于C#和Blazor…...

【3D捏脸功能实现】
文章目录 一、技术方案介绍二、技术核心三、底层技术实现选型进行模型建模编写逻辑代码 四、功能落地五、总结 一、技术方案介绍 3D捏脸功能是一种利用3D技术实现用户自定义头像的功能。通常实现这种功能需要以下技术: 3D建模技术。通过3D建模技术可以创建一个可以…...
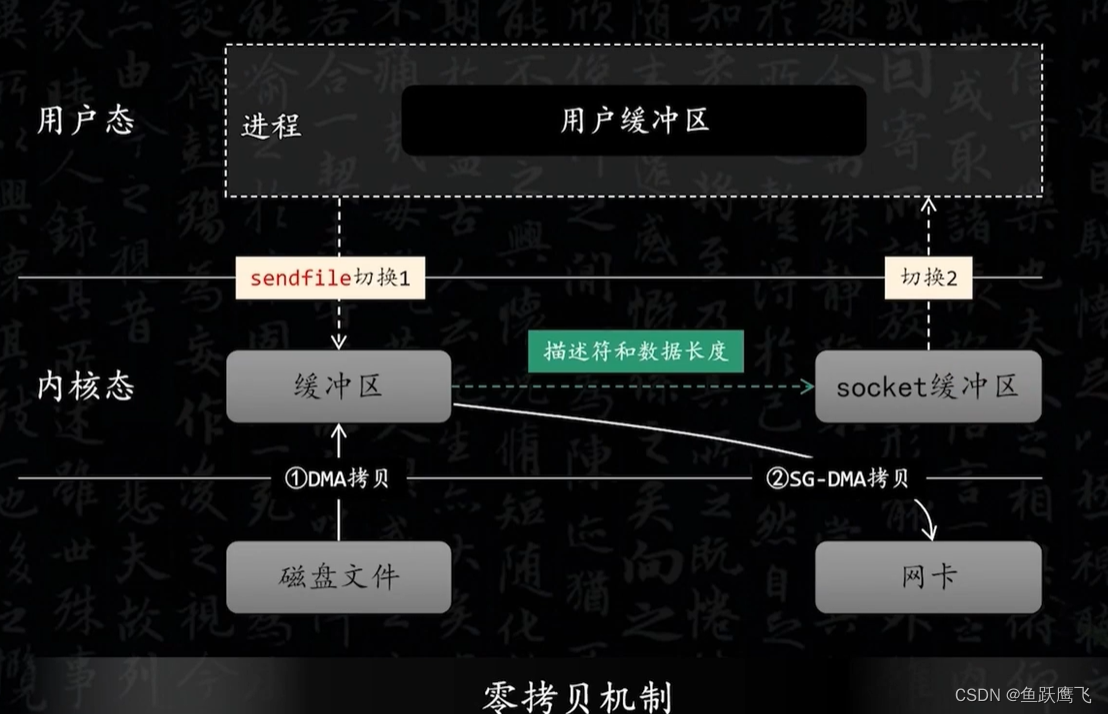
Kafka的零拷贝
传统的IO模型 如果要把磁盘中的某个文件发送到远程服务器需要经历以下几个步骤 (1) 从磁盘中读取文件的内容,然后拷贝到内核缓冲区 (2) CPU把内核缓冲区的数据赋值到用户空间的缓冲区 (3) 在用户程序中调用write方法,把用户缓冲区的数据拷贝到内核下面…...

如何使用Python进行数据分析?
Python是一个非常流行的编程语言,也是数据科学家和数据分析师最常用的语言之一。 Python的生态系统非常丰富,有很多强大的库和工具可以用来进行数据分析,如NumPy、Pandas、Matplotlib、SciPy等。 Python教程,8天python从入门到精…...

概率论与数理统计复习总结3
概率论与数理统计复习总结,仅供笔者复习使用,参考教材: 《概率论与数理统计》/ 荣腾中主编. — 第 2 版. 高等教育出版社《2024高途考研数学——概率基础精讲》王喆 概率论与数理统计实际上是两个互补的分支:概率论 在 已知随机…...

PHP正则绕过解析
正则绕过 正则表达式PHP正则回溯PHP中的NULL和false回溯案例案例1案例2 正则表达式 在正则中有许多特殊的字符,不能直接使用,需要使用转义符\。如:$,(,),*,,.,?,[,,^,{。 这里大家会有疑问:为啥小括号(),这个就需要两个来转义&a…...

Hive巡检脚本
Hive巡检脚本的示例: #!/bin/bash# 设置Hive连接信息 HIVE_HOST"your_hive_host" HIVE_PORT"your_hive_port" HIVE_USER"your_hive_username" HIVE_PASSWORD"your_hive_password"# 设置巡检结果输出文件路径 OUTPUT_FILE&…...
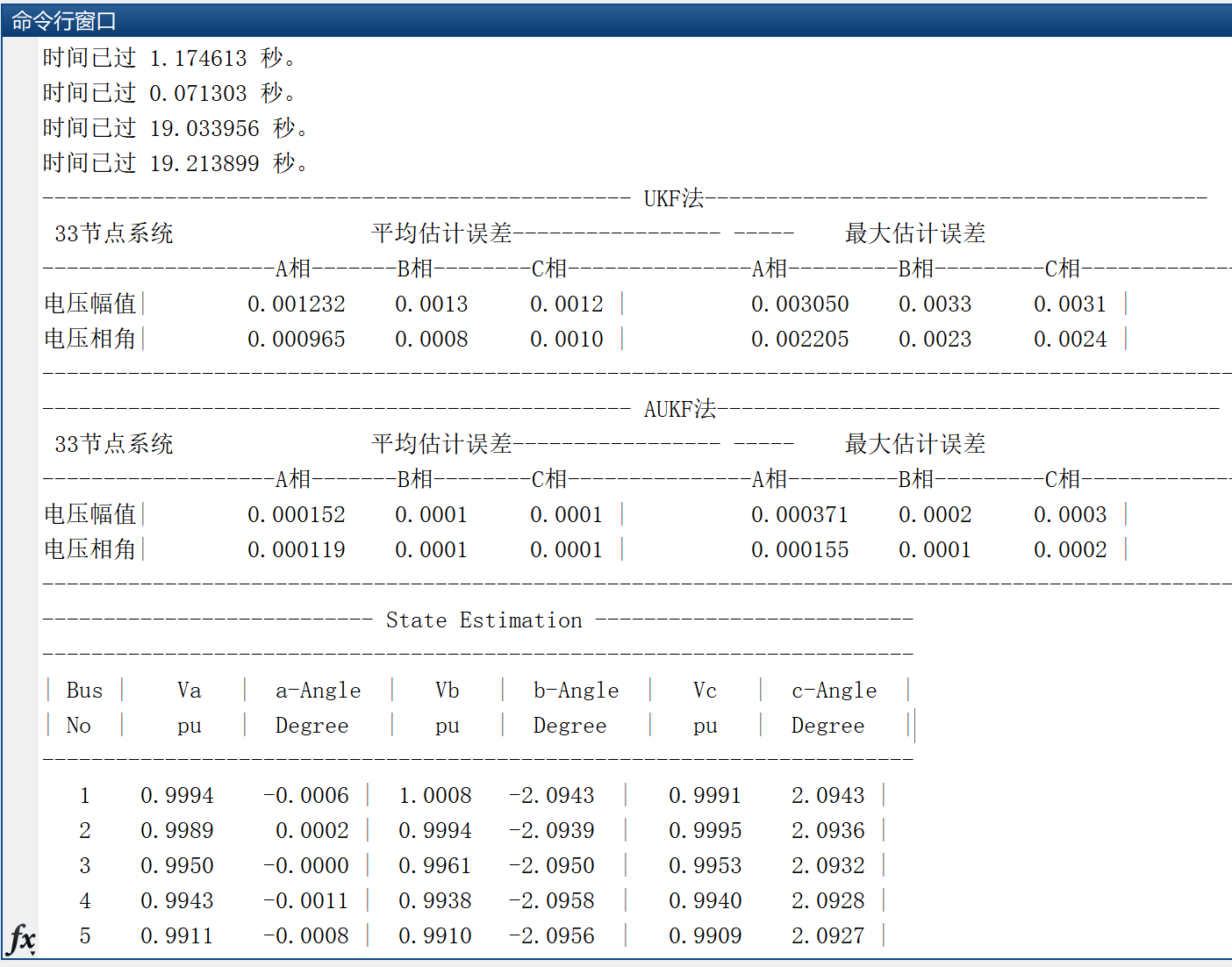
【状态估计】基于UKF法、AUKF法的电力系统三相状态估计研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
webpack复习
webpack webpack复习 webpack基本配置 拆分配置 - 公共配置 生产环境配置 开发环境配置 使用merge webpack-dev-server 启动本地服务 在公共中引入babel-loader处理es6 webpack高级配置 多入口文件 enty 入口为一个对象 里面的key为入口名 value为入口文件路径 例如 pa…...

开始学习 Kafka,一文掌握基本概念|Kafka 系列 一
如果你还不了解 Kafka,或者也打算深入探索、系统学习,那么欢迎有同样目标的小伙伴可以加群交流,让学习之路不再孤独。 一个人可能走的很快,但是一群人会走的更远。(后台回复:加群) 点击上方“后…...
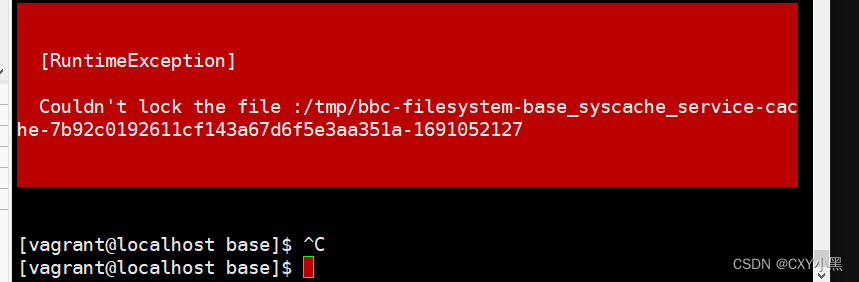
Couldn‘t lock the file :/tmp/bbc-filesystem-base_syscache_service
解决方案: 进去带这个目录,然后切换成root用户,将它删除...

vscode 通过mongoose 连接mongodb atlas
了解mongodb 的项目结构 1.代表集群名称 > 2.代表数据库名称>3.代表每个 collection名称 三者范围为从大到小的关系 (一对多)。每个集群有不同的连接地址、用户信息(Database Access)、ip配置信息(Network Acce…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...
