【机器学习】西瓜书习题3.3Python编程实现对数几率回归
参考代码
结合自己的理解,添加注释。
代码
- 导入相关的库
import numpy as np
import pandas as pd
import matplotlib
from matplotlib import pyplot as plt
from sklearn import linear_model
- 导入数据,进行数据处理和特征工程
# 1.数据处理,特征工程
data_path = 'watermelon3_0_Ch.csv'
data = pd.read_csv(data_path).values
# 取所有行的第10列(标签列)进行判断
is_good = data[:,9] == '是'
is_bad = data[:,9] == '否'
# 按照数据集3.0α,强制转换数据类型
X = data[:,7:9].astype(float)
y = data[:,9]
y[y=='是'] = 1
y[y=='否'] = 0
y = y.astype(int)
- 定义若干需要使用的函数
y = 1 1 + e − x y= \frac{1}{1+e^{-x}} y=1+e−x1
def sigmoid(x):"""构造对数几率函数,它是一种sigmoid函数"""s = 1/(1+np.exp(-x))return s
ℓ ( β ) = ∑ i = 1 m ( − y i β T x ^ i + l n ( 1 + e β T x ^ i ) ) \ell(\beta) = \sum_{i=1}^{m}(-y_{i}\beta^{T} \hat{x}_{i} + ln(1+e^{\beta^{T} \hat{x}_{i}})) ℓ(β)=i=1∑m(−yiβTx^i+ln(1+eβTx^i))
def J_cost(X,y,beta):""":param X: sample array, shape(n_samples, n_features):param y: array-like, shape (n_samples,):param beta: the beta in formula 3.27 , shape(n_features + 1, ) or (n_features + 1, 1):return: the result of formula 3.27"""# 构造x_hat,np.c_ 用于连接两个矩阵,规模是(X.row行,X.column+1列)X_hat = np.c_[X, np.ones((X.shape[0],1))]# β和y均reshape为1列,规模是(X.column+1行,1列)beta = beta.reshape(-1,1)y = y.reshape(-1,1)# 计算最大化似然函数的相反数L_beta = -y * np.dot(X_hat,beta) + np.log(1+np.exp(np.dot(X_hat,beta)))# 返回式3.27的结果return L_beta.sum()
β = ( w ; b ) \beta = (w; b) β=(w;b)
def initialize_beta(column):"""初始化β,对应式3.26的假设,规模是(X.column+1行,1列),x_hat规模是(17行,X.column+1列)"""# numpy.random.randn(d0,d1,…,dn)# randn函数返回一个或一组样本,具有标准正态分布。标准正态分布又称为u分布,是以0为均值、以1为标准差的正态分布,记为N(0,1)# dn表格每个维度# 返回值为指定维度的arraybeta = np.random.randn(column+1,1)*0.5+1return beta
∂ ℓ ( β ) ∂ β = − ∑ i = 1 m x ^ i ( y i − p 1 ( x ^ i ; β ) ) \frac{\partial \ell(\beta)}{\partial \beta} = -\sum_{i=1}^{m}\hat{x}_{i}(y_{i}-p_{1}(\hat{x}_{i};\beta)) ∂β∂ℓ(β)=−i=1∑mx^i(yi−p1(x^i;β))
def gradient(X,y,beta):"""compute the first derivative of J(i.e. formula 3.27) with respect to beta i.e. formula 3.30计算式3.27的一阶导数----------------------------------------------------:param X: sample array, shape(n_samples, n_features):param y: array-like, shape (n_samples,):param beta: the beta in formula 3.27 , shape(n_features + 1, ) or (n_features + 1, 1):return:"""# 构造x_hat,np.c_ 用于连接两个矩阵,规模是(X.row行,X.column+1列)X_hat = np.c_[X, np.ones((X.shape[0],1))]# β和y均reshape为1列,规模是(X.column+1行,1列)beta = beta.reshape(-1,1)y = y.reshape(-1,1)# 计算p1(X_hat,beta)p1 = sigmoid(np.dot(X_hat,beta))gra = (-X_hat*(y-p1)).sum(0)return gra.reshape(-1,1)
∂ 2 ℓ ( β ) ∂ β ∂ β T = ∑ i = 1 m x ^ i x ^ i T p 1 ( x ^ i ; β ) ( 1 − p 1 ( x ^ i ; β ) ) \frac{\partial^2 \ell(\beta)}{\partial \beta \partial \beta^T} = \sum_{i=1}^{m}\hat{x}_{i}\hat{x}_{i}^Tp_{1}(\hat{x}_{i};\beta)(1-p_{1}(\hat{x}_{i};\beta)) ∂β∂βT∂2ℓ(β)=i=1∑mx^ix^iTp1(x^i;β)(1−p1(x^i;β))
def hessian(X,y,beta):'''compute the second derivative of J(i.e. formula 3.27) with respect to beta i.e. formula 3.31计算式3.27的二阶导数----------------------------------:param X: sample array, shape(n_samples, n_features):param y: array-like, shape (n_samples,):param beta: the beta in formula 3.27 , shape(n_features + 1, ) or (n_features + 1, 1):return:'''# 构造x_hat,np.c_ 用于连接两个矩阵,规模是(X.row行,X.column+1列)X_hat = np.c_[X, np.ones((X.shape[0],1))]# β和y均reshape为1列,规模是(X.column+1行,1列)beta = beta.reshape(-1,1)y = y.reshape(-1,1)# 计算p1(X_hat,beta)p1 = sigmoid(np.dot(X_hat,beta))m,n=X.shape# np.eye()返回的是一个二维2的数组(N,M),对角线的地方为1,其余的地方为0.P = np.eye(m)*p1*(1-p1)assert P.shape[0] == P.shape[1]# X_hat.T是X_hat的转置return np.dot(np.dot(X_hat.T,P),X_hat)
使用梯度下降法求解
def update_parameters_gradDesc(X,y,beta,learning_rate,num_iterations,print_cost):"""update parameters with gradient descent method"""for i in range(num_iterations):grad = gradient(X,y,beta)beta = beta - learning_rate*grad# print_cost为true时,并且迭代为10的倍数时,打印本次迭代的costif (i%10==0)&print_cost:print('{}th iteration, cost is {}'.format(i,J_cost(X,y,beta)))return betadef logistic_model(X,y,print_cost=False,method='gradDesc',learning_rate=1.2,num_iterations=1000):""":param method: str 'gradDesc'or'Newton'"""# 得到X的规模row,column = X.shape# 初始化βbeta = initialize_beta(column)if method == 'gradDesc':return update_parameters_gradDesc(X,y,beta,learning_rate,num_iterations,print_cost)elif method == 'Newton':return update_parameters_newton(X,y,beta,print_cost,num_iterations)else:raise ValueError('Unknown solver %s' % method)
- 可视化结果
# 1.可视化数据点
# 设置字体为楷体
matplotlib.rcParams['font.sans-serif'] = ['KaiTi']
plt.scatter(data[:, 7][is_good], data[:, 8][is_good], c='b', marker='o') #c参数是颜色,marker是标记
plt.scatter(data[:, 7][is_bad], data[:, 8][is_bad], c='r', marker='x')
# 设置横轴坐标标题
plt.xlabel('密度')
plt.ylabel('含糖量')# 2.可视化自己写的模型
# 学习得到模型
beta = logistic_model(X,y,print_cost=True,method='gradDesc',learning_rate=0.3, num_iterations=1000)
# 得到模型参数及偏置(截距)
w1, w2, intercept = beta
x1 = np.linspace(0, 1)
y1 = -(w1 * x1 + intercept) / w2
ax1, = plt.plot(x1, y1, label=r'my_logistic_gradDesc')# 3.可视化sklearn的对率回归模型,进行对比
lr = linear_model.LogisticRegression(solver='lbfgs', C=1000) # 注意sklearn的逻辑回归中,C越大表示正则化程度越低。
lr.fit(X, y)
lr_beta = np.c_[lr.coef_, lr.intercept_]
print(J_cost(X, y, lr_beta))
# 可视化sklearn LogisticRegression 模型结果
w1_sk, w2_sk = lr.coef_[0, :]
x2 = np.linspace(0, 1)
y2 = -(w1_sk * x2 + lr.intercept_) / w2
ax2, = plt.plot(x2, y2, label=r'sklearn_logistic')
plt.legend(loc='upper right')
plt.show()
可视化结果如下:
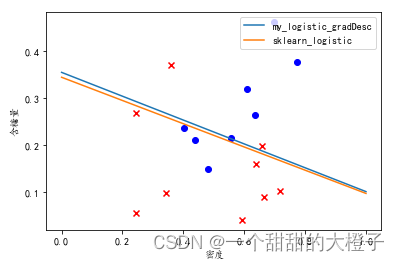
相关文章:

【机器学习】西瓜书习题3.3Python编程实现对数几率回归
参考代码 结合自己的理解,添加注释。 代码 导入相关的库 import numpy as np import pandas as pd import matplotlib from matplotlib import pyplot as plt from sklearn import linear_model导入数据,进行数据处理和特征工程 # 1.数据处理&#x…...
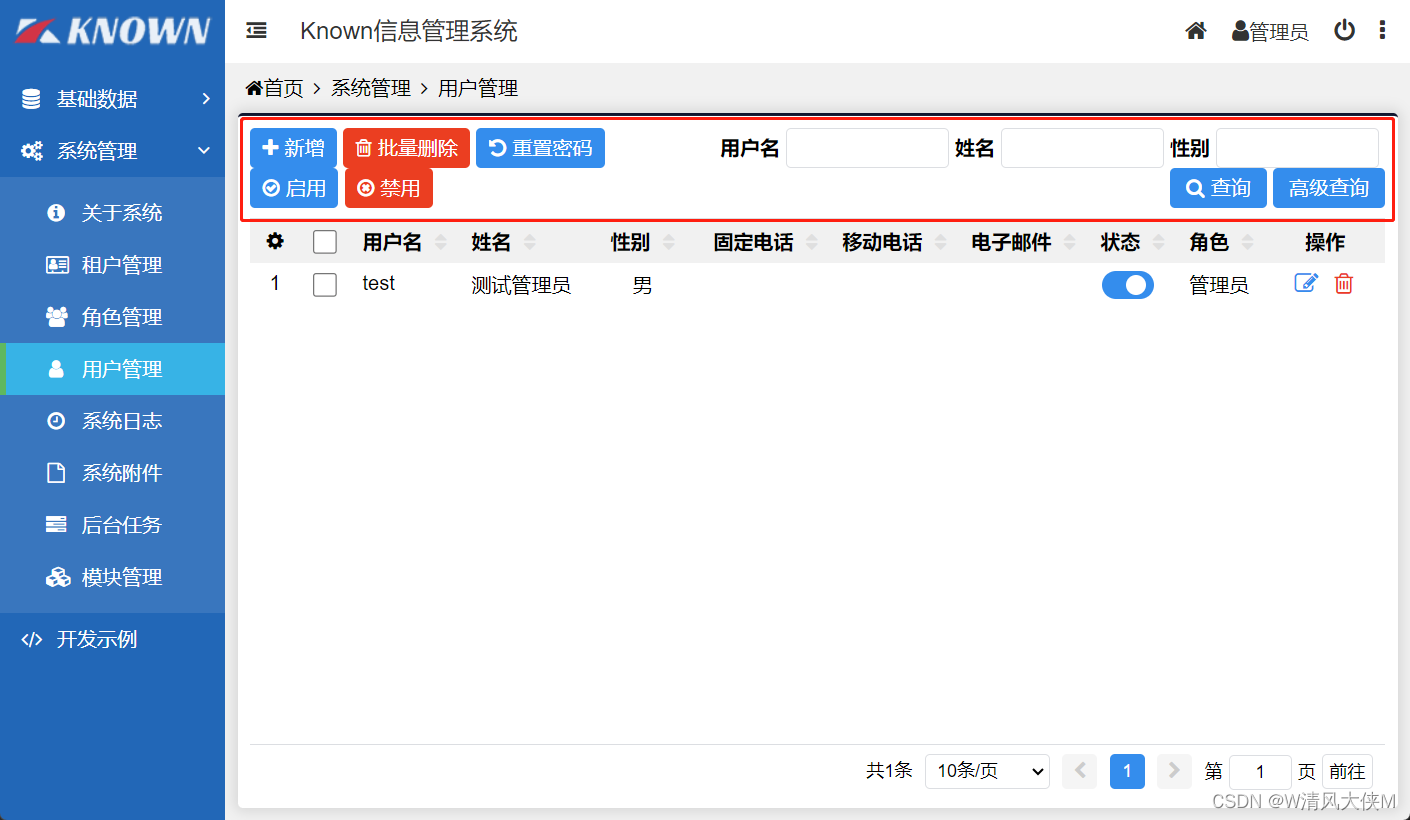
Blazor前后端框架Known-V1.2.9
V1.2.9 Known是基于C#和Blazor开发的前后端分离快速开发框架,开箱即用,跨平台,一处代码,多处运行。 Gitee: https://gitee.com/known/KnownGithub:https://github.com/known/Known 概述 基于C#和Blazor…...

【3D捏脸功能实现】
文章目录 一、技术方案介绍二、技术核心三、底层技术实现选型进行模型建模编写逻辑代码 四、功能落地五、总结 一、技术方案介绍 3D捏脸功能是一种利用3D技术实现用户自定义头像的功能。通常实现这种功能需要以下技术: 3D建模技术。通过3D建模技术可以创建一个可以…...
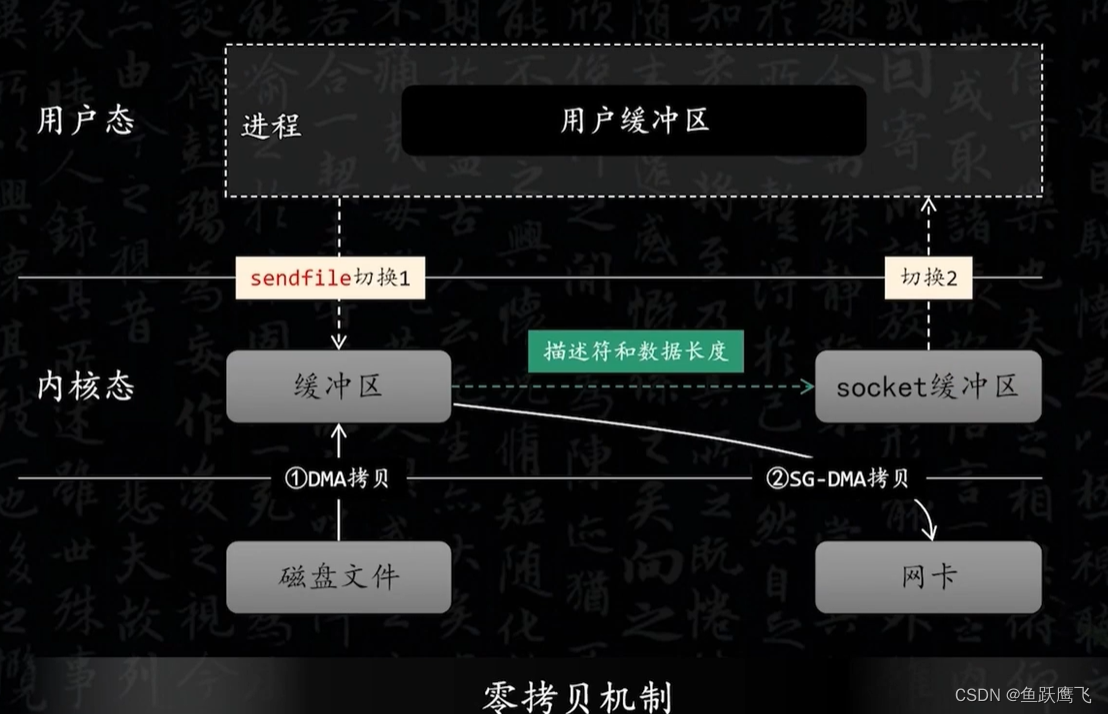
Kafka的零拷贝
传统的IO模型 如果要把磁盘中的某个文件发送到远程服务器需要经历以下几个步骤 (1) 从磁盘中读取文件的内容,然后拷贝到内核缓冲区 (2) CPU把内核缓冲区的数据赋值到用户空间的缓冲区 (3) 在用户程序中调用write方法,把用户缓冲区的数据拷贝到内核下面…...

如何使用Python进行数据分析?
Python是一个非常流行的编程语言,也是数据科学家和数据分析师最常用的语言之一。 Python的生态系统非常丰富,有很多强大的库和工具可以用来进行数据分析,如NumPy、Pandas、Matplotlib、SciPy等。 Python教程,8天python从入门到精…...

概率论与数理统计复习总结3
概率论与数理统计复习总结,仅供笔者复习使用,参考教材: 《概率论与数理统计》/ 荣腾中主编. — 第 2 版. 高等教育出版社《2024高途考研数学——概率基础精讲》王喆 概率论与数理统计实际上是两个互补的分支:概率论 在 已知随机…...

PHP正则绕过解析
正则绕过 正则表达式PHP正则回溯PHP中的NULL和false回溯案例案例1案例2 正则表达式 在正则中有许多特殊的字符,不能直接使用,需要使用转义符\。如:$,(,),*,,.,?,[,,^,{。 这里大家会有疑问:为啥小括号(),这个就需要两个来转义&a…...

Hive巡检脚本
Hive巡检脚本的示例: #!/bin/bash# 设置Hive连接信息 HIVE_HOST"your_hive_host" HIVE_PORT"your_hive_port" HIVE_USER"your_hive_username" HIVE_PASSWORD"your_hive_password"# 设置巡检结果输出文件路径 OUTPUT_FILE&…...
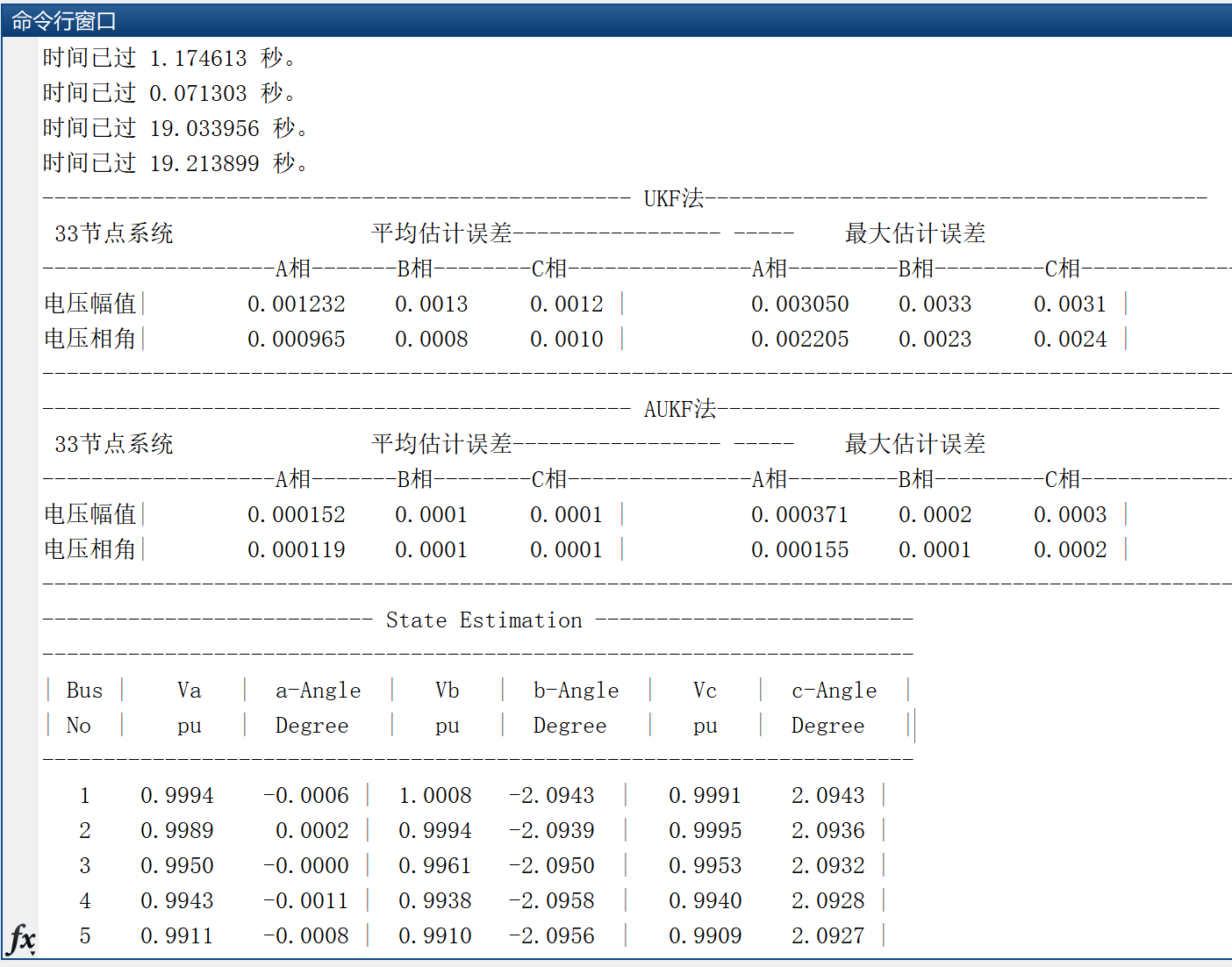
【状态估计】基于UKF法、AUKF法的电力系统三相状态估计研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
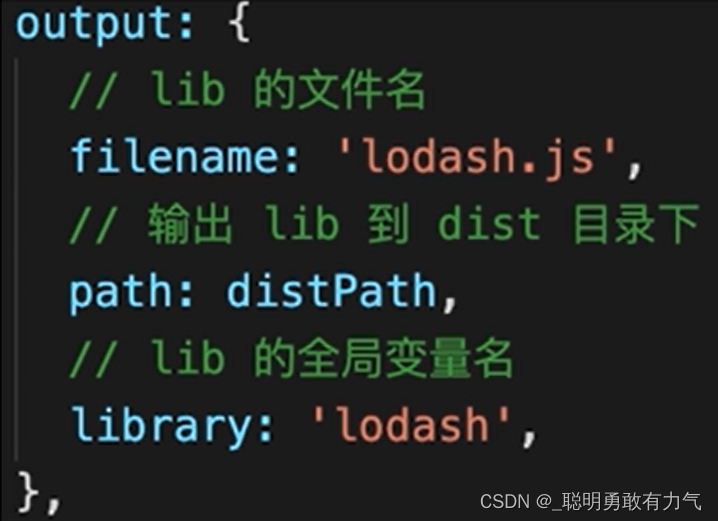
webpack复习
webpack webpack复习 webpack基本配置 拆分配置 - 公共配置 生产环境配置 开发环境配置 使用merge webpack-dev-server 启动本地服务 在公共中引入babel-loader处理es6 webpack高级配置 多入口文件 enty 入口为一个对象 里面的key为入口名 value为入口文件路径 例如 pa…...

开始学习 Kafka,一文掌握基本概念|Kafka 系列 一
如果你还不了解 Kafka,或者也打算深入探索、系统学习,那么欢迎有同样目标的小伙伴可以加群交流,让学习之路不再孤独。 一个人可能走的很快,但是一群人会走的更远。(后台回复:加群) 点击上方“后…...
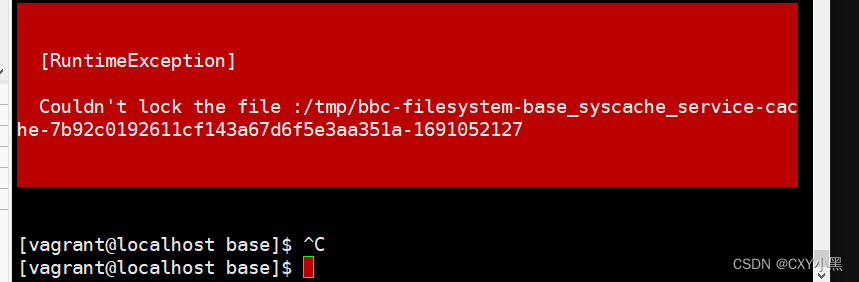
Couldn‘t lock the file :/tmp/bbc-filesystem-base_syscache_service
解决方案: 进去带这个目录,然后切换成root用户,将它删除...

vscode 通过mongoose 连接mongodb atlas
了解mongodb 的项目结构 1.代表集群名称 > 2.代表数据库名称>3.代表每个 collection名称 三者范围为从大到小的关系 (一对多)。每个集群有不同的连接地址、用户信息(Database Access)、ip配置信息(Network Acce…...

记录 Vue3 + Ts 类型使用
阅读时长: 10 分钟 本文内容:记录在 Vue3 中使用 ts 时的各种写法. 类型大小写 vue3 ts 项目中,类型一会儿大写一会儿小写。 怎么区分与基础类型使用? String、string、Number、number、Boolean、boolean … 在 js 中, 以 string 与 String…...
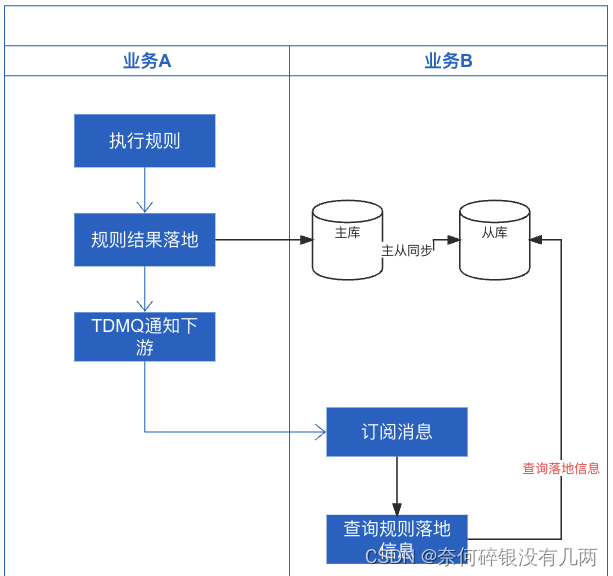
主从同步带来的业务问题
目录 一: 目前的业务问题二:如何平衡主从不同步和业务隔离?三:解决方案 一: 目前的业务问题 业务A会跑一些规则, 跑完会把规则结果信息落地(落地到主库), 然后会通过TDM…...

主动带宽控制工具
停机和带宽过度使用是任何组织都无法避免的两个问题。随着企业采用 BYOD 文化,通过网络的流量负载可能很重,导致网络拥塞并使网络容易受到网络攻击。为了解决这个问题,企业需要全面的监控策略来保护网络,当看似大量的流量进入网络…...

数据采集的方法有哪些?
近年来,国家和各大企业都在部署大数据战略。“大数据”这个词也越来越频繁地出现在我们的生活中。当我们在进行网上冲浪时,页面总会跳出我们想要搜索的相关产品或关联事物。大数据,似乎总是能够“算”出我们“心中所想”。那么,大…...

linux重新学习-纪录篇
前言: 正式学习linux的时候,除了那些命令之外,更多的是对于这个系统的重新认知。 linux的身世? 在上世纪90年代,那时候计算机非常的珍贵,配置也很一般般,系统也贵,所以没啥人用,在当…...
为机器人装“大脑” 谷歌发布RT-2大模型
大语言模型不仅能让应用变得更智能,还将让机器人学会举一反三。在谷歌发布RT-1大模型仅半年后,专用于机器人的RT-2大模型于近期面世,它能让机器人学习互联网上的文本和图像,并具备逻辑推理能力。 该模型为机器人智能带来显著升级…...
JavaEE 面试常见问题
一、常见的 ORM 框架有哪些? 1.Mybatis Mybatis 是一种典型的半自动的 ORM 框架,所谓的半自动,是因为还需要手动的写 SQL 语句,再由框架根据 SQL 及 传入数据来组装为要执行的 SQL 。其优点为: 1. 因为由程序员…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...
