概率论与数理统计复习总结3
概率论与数理统计复习总结,仅供笔者复习使用,参考教材:
- 《概率论与数理统计》/ 荣腾中主编. — 第 2 版. 高等教育出版社
- 《2024高途考研数学——概率基础精讲》王喆
概率论与数理统计实际上是两个互补的分支:概率论 在 已知随机变量及其概率分布 的基础上去描述随机现象的统计规律、挖掘随机变量的数字特征与数学性质、计算随机事件的发生概率;数理统计 则是通过随机现象来研究其统计规律性,即通过收集、整理和分析随机变量的观测数据,对随机变量的性质和特征做出合理的推断或预测。
本文主要内容为:数理统计2;
概率论 部分见 概率论与数理统计复习总结1;
数理统计1 部分见 概率论与数理统计复习总结2;
数理统计2 部分见 概率论与数理统计复习总结3;
目录
- 八. 假设检验
- 1. 假设检验的基本原理
- 2. 假设检验的步骤
- 3. 假设检验的两类错误
- 4. 参数假设检验
- 4.1 单个正态总体的参数假设检验
八. 假设检验
假设检验利用样本信息对总体的某种假设进行检验,用于推断数据样本中的差异是否真实存在或是由于随机变异导致的。假设检验一般分为参数假设检验与非参数假设检验,本节主要介绍参数假设检验,即对总体分布中未知参数的假设检验。
1. 假设检验的基本原理
假设检验的基本原理是通过样本数据来对总体特征提出的假设进行推断,通过比较观察到的样本统计量(例如平均值、比例、方差等)与假设中的理论预期值,来判断样本数据是否支持或反对该假设。这样的假设叫做原假设或零假设。
- 原假设:也叫零假设,记为 H 0 H_0 H0。原假设是关于总体特征的默认假设,通常表述为无效、无差异或无影响的假设,如 μ = 8000 \mu=8000 μ=8000、 μ 1 = μ 2 \mu_1=\mu_2 μ1=μ2 等;
- 备择假设:记为 H 1 H_1 H1。备择假设一般是我们希望支持的假设,它表述了我们认为有足够证据支持的观点或猜测。在假设检验中,我们试图通过数据证明备择假设成立,从而拒绝原假设。备择假设可以是双侧的(two-tailed),表明总体特征与原假设有明显差异;也可以是单侧的(one-tailed),表明总体特征在某个方向上显著大于或小于原假设。如 μ ≠ 8000 \mu \neq 8000 μ=8000、 μ 1 ≠ μ 2 \mu_1 \neq \mu_2 μ1=μ2 等;
- 显著性水平:假设检验中事先设定的一个临界值,通常用符号 α \alpha α 表示,用于判断在样本数据中观察到的统计显著性,决定了在假设检验中拒绝原假设的标准,一般取 0.05 或 0.01;
- 拒绝域:样本数据的一个子集,记为 X 0 \mathscr{X}_0 X0。当样本数据落入这个区域时,我们将拒绝原假设,因为拒绝域包含的样本数据在原假设成立的情况下发生的概率较小,我们认为这样的结果对原假设提供了足够的反对证据,从而拒绝原假设。通常,拒绝域的边界由显著性水平 α \alpha α 确定;
- 接受域:样本数据的另一个子集,也是拒绝域的补集,记为 X 0 ‾ \overline{\mathscr{X}_0} X0。当样本数据落入这个区域时,我们将接受原假设,因为接受域包含的样本数据在原假设成立的情况下发生的概率较大,我们认为这样的结果并不足以提供充分证据来拒绝原假设;
2. 假设检验的步骤
- 提出统计假设:明确原假设和备择假设;
- 选择检验统计量:对原假设 H 0 H_0 H0 通过 检验统计量 W = W ( X 1 , X 2 ⋯ , X n ) W=W\left(X_1, X_2 \cdots, X_n\right) W=W(X1,X2⋯,Xn) 的判断需要确定 H 0 H_0 H0 成立条件下统计量 W W W 的精确分布或极限分布,以便能根据显著性水平 α \alpha α 确定 H 0 H_0 H0 的拒绝域;
一般地,针对正态总体 N ( μ , σ 2 ) N\left(\mu, \sigma^2\right) N(μ,σ2) 的参数 μ \mu μ 提出假设 H 0 : μ = μ 0 H_0: \mu=\mu_0 H0:μ=μ0,则选择统计量 U = X ˉ − μ 0 σ n ( σ 2 U=\frac{\bar{X}-\mu_0}{\sigma} \sqrt{n}\left(\sigma^2\right. U=σXˉ−μ0n(σ2 已知) 或 T = X ˉ − μ 0 S n T=\frac{\bar{X}-\mu_0}{S} \sqrt{n} T=SXˉ−μ0n ( σ 2 \sigma^2 σ2 末知);针对正态总体 N ( μ , σ 2 ) N\left(\mu, \sigma^2\right) N(μ,σ2) 的参数 σ 2 \sigma^2 σ2 提出假设 H 0 : σ 2 = σ 0 2 H_0: \sigma^2=\sigma_0^2 H0:σ2=σ02,则选择统计量 χ 2 = ( n − 1 ) S 2 σ 0 2 \chi^2=\frac{(n-1) S^2}{\sigma_0^2} χ2=σ02(n−1)S2;针对总体 B ( 1 , p ) B(1, p) B(1,p) 的参数 p p p 提出假设 H 0 : p = p 0 H_0: p=p_0 H0:p=p0,则选择统计量 U = X ˉ − p 0 p 0 ( 1 − p 0 ) n U=\frac{\bar{X}-p_0}{\sqrt{p_0\left(1-p_0\right)}} \sqrt{n} U=p0(1−p0)Xˉ−p0n 等。通常检验方法由统计量的分布来命名,如 U U U 检验法、 t t t 检验法、 χ 2 \chi^2 χ2 检验法、 F F F 检验法等。
- 确立拒绝域形式和拒绝域:通过备择假设 H 1 H_1 H1 来确立拒绝域的形式。由显著性水平 α \alpha α,拒绝域 X 0 \mathscr{X}_0 X0 的形式,检验统计量及分布和 P { ( X 1 , X 2 , ⋯ , X n ) ∈ X 0 ∣ H 0 成立 } ⩽ α P\left\{\left(X_1, X_2, \cdots, X_n\right) \in \mathscr{X}_0 \mid H_0 \text { 成立 } \right\} \leqslant \alpha P{(X1,X2,⋯,Xn)∈X0∣H0 成立 }⩽α 可确定待定常数 c c c,这就确定了拒绝域 X 0 \mathscr{X}_0 X0,通常 α \alpha α 选取 0.01,0.05 或 0.10;
一般地,如果 H 1 : μ ≠ μ 0 H_1: \mu \neq \mu_0 H1:μ=μ0 表示总体均值 μ \mu μ 与 μ 0 \mu_0 μ0 有显著差异,用 X ˉ \bar{X} Xˉ 去估计参数 μ \mu μ 和引人待定常数 c c c 预估差异大小,即小概率事件为 { X ˉ − μ 0 < − c } ∪ { X ˉ − μ 0 > \left\{\bar{X}-\mu_0<-c\right\} \cup\left\{\bar{X}-\mu_0>\right. {Xˉ−μ0<−c}∪{Xˉ−μ0> c } c\} c},那么拒绝域形式为 { ∣ X ˉ − μ 0 ∣ > c } \left\{\left|\bar{X}-\mu_0\right|>c\right\} { Xˉ−μ0 >c},称 H 1 : μ ≠ μ 0 H_1: \mu \neq \mu_0 H1:μ=μ0 为双侧假设检验问题;如果 H 1 : μ > μ 0 H_1: \mu>\mu_0 H1:μ>μ0,则选择拒绝域 { X ˉ − μ 0 > c } \left\{\bar{X}-\mu_0>c\right\} {Xˉ−μ0>c},称 H 1 : μ > μ 0 H_1: \mu>\mu_0 H1:μ>μ0 为单侧假设检验问题。
- 作出判断或决策:根据抽样信息,计算检验统计量的样本值 w = W ( x 1 , x 2 , ⋯ , x n ) w=W\left(x_1, x_2, \cdots, x_n\right) w=W(x1,x2,⋯,xn)。若 ( x 1 \left(x_1\right. (x1, x 2 , ⋯ , x n ) ∈ X 0 \left.x_2, \cdots, x_n\right) \in \mathscr{X}_0 x2,⋯,xn)∈X0,则拒绝 H 0 H_0 H0,接受 H 1 H_1 H1;否则接受 H 0 H_0 H0;
3. 假设检验的两类错误
由于抽样的随机性和小概率原理,假设检验所作出的判断可能与事实不符合,出现推断错误。把拒绝 H 0 H_0 H0 可能犯的错误称为第Ⅰ类错误或弃真错误;把接受 H 0 H_0 H0 的判断可能犯的错误称为第Ⅱ类错误或纳伪错误。
| \真实情况 假设检验结果\ | H 0 H_0 H0 成立 | H 0 H_0 H0 不成立 |
|---|---|---|
| 拒绝 H 0 H_0 H0 | 犯第Ⅰ类错误(弃真错误) | 推断正确 |
| 接受 H 0 H_0 H0 | 推断正确 | 犯第Ⅱ类错误(纳伪错误) |
- 第Ⅰ类错误:原假设 H 0 H_0 H0 为真,由于样本的随机性,使样本观测值落入拒绝域 X 0 \mathscr{X}_0 X0 中,判断为拒绝 H 0 H_0 H0。错误的概率记为 α \alpha α:
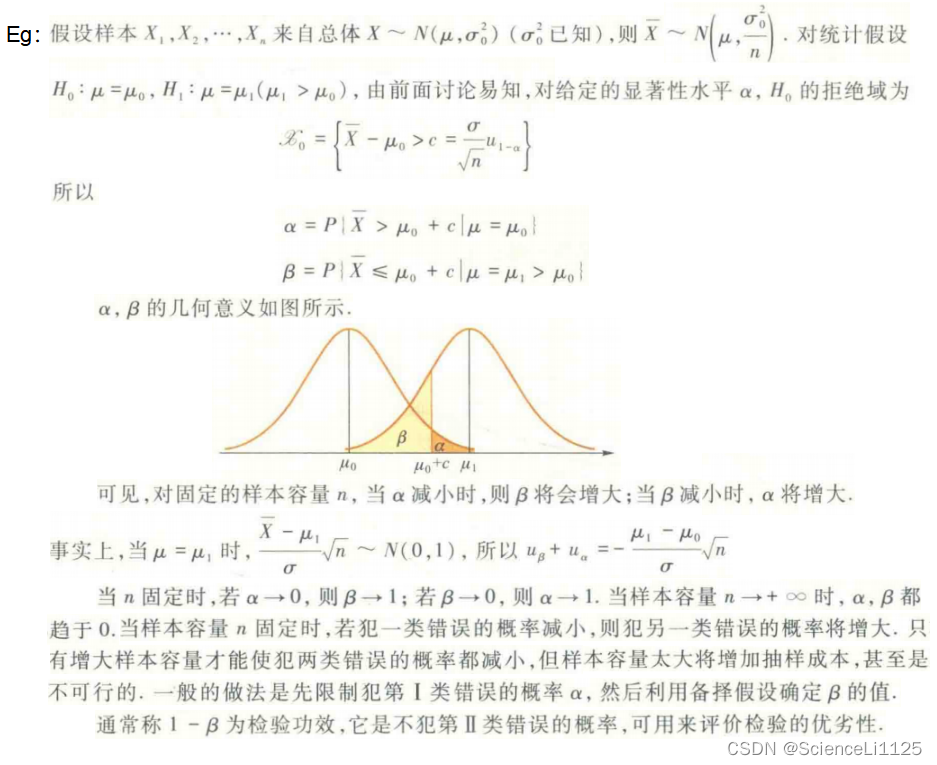
α = P { 拒绝 H 0 ∣ H 0 成立 } = P { ( X 1 , X 2 , ⋯ , X n ) ∈ X 0 ∣ H 0 成立 } \alpha = P\{拒绝 H_0 | H_0 成立\} = P\left\{\left(X_1, X_2, \cdots, X_n\right) \in \mathscr{X}_0 \mid H_0 成立 \right\} α=P{拒绝H0∣H0成立}=P{(X1,X2,⋯,Xn)∈X0∣H0成立} - 第Ⅱ类错误:原假设 H 0 H_0 H0 为假,判断为接受 H 0 H_0 H0;错误的概率记为 β \beta β:
β = P { 接受 H 0 ∣ H 0 不成立 } = P { ( X 1 , X 2 , ⋯ , X n ) ∈ X 0 ‾ ∣ H 0 不成立 } \beta = P\{接受 H_0 | H_0 不成立\} = P\left\{\left(X_1, X_2, \cdots, X_n\right) \in \overline{\mathscr{X}_0} \mid H_0 不成立 \right\} β=P{接受H0∣H0不成立}=P{(X1,X2,⋯,Xn)∈X0∣H0不成立}
在样本容量固定的条件下,减少犯一类错误的概率,就会增加犯另一类错误的概率。举例如下:
4. 参数假设检验
实际问题中很多随机变量服从或近似服从正态分布,因此这节重点介绍单个正态总体的参数假设检验。
4.1 单个正态总体的参数假设检验
-
参数 μ \mu μ 的假设检验:

-
参数 σ 2 \sigma^2 σ2 的假设检验( μ \mu μ 未知):

拒绝域同时在数轴左右两侧的假设检验称为 双侧假设检验 或双尾假设检验,拒绝域在数轴左侧或右侧的假设检验分别称为左侧假设检验或右侧假设检验,统称为 单侧检验 或单尾检验。双侧假设检验关注的是 总体参数是否有明显的变化,而单侧假设检验关注 总体参数明显变化的方向,左侧检验关注总体参数是否明显减少,右侧检验关注总体参数是否明显增加。举例如下:
相关文章:

概率论与数理统计复习总结3
概率论与数理统计复习总结,仅供笔者复习使用,参考教材: 《概率论与数理统计》/ 荣腾中主编. — 第 2 版. 高等教育出版社《2024高途考研数学——概率基础精讲》王喆 概率论与数理统计实际上是两个互补的分支:概率论 在 已知随机…...

PHP正则绕过解析
正则绕过 正则表达式PHP正则回溯PHP中的NULL和false回溯案例案例1案例2 正则表达式 在正则中有许多特殊的字符,不能直接使用,需要使用转义符\。如:$,(,),*,,.,?,[,,^,{。 这里大家会有疑问:为啥小括号(),这个就需要两个来转义&a…...

Hive巡检脚本
Hive巡检脚本的示例: #!/bin/bash# 设置Hive连接信息 HIVE_HOST"your_hive_host" HIVE_PORT"your_hive_port" HIVE_USER"your_hive_username" HIVE_PASSWORD"your_hive_password"# 设置巡检结果输出文件路径 OUTPUT_FILE&…...
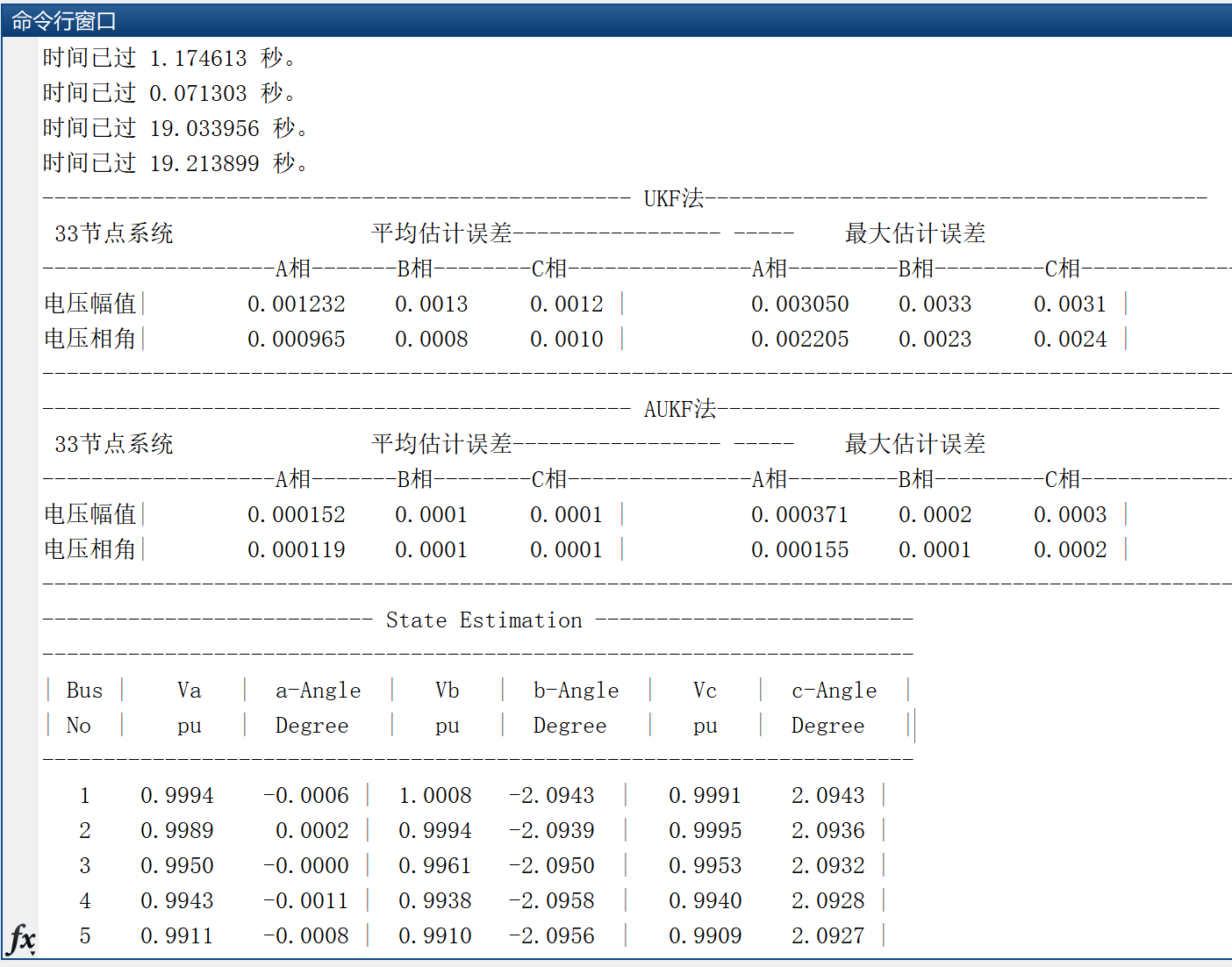
【状态估计】基于UKF法、AUKF法的电力系统三相状态估计研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
webpack复习
webpack webpack复习 webpack基本配置 拆分配置 - 公共配置 生产环境配置 开发环境配置 使用merge webpack-dev-server 启动本地服务 在公共中引入babel-loader处理es6 webpack高级配置 多入口文件 enty 入口为一个对象 里面的key为入口名 value为入口文件路径 例如 pa…...

开始学习 Kafka,一文掌握基本概念|Kafka 系列 一
如果你还不了解 Kafka,或者也打算深入探索、系统学习,那么欢迎有同样目标的小伙伴可以加群交流,让学习之路不再孤独。 一个人可能走的很快,但是一群人会走的更远。(后台回复:加群) 点击上方“后…...
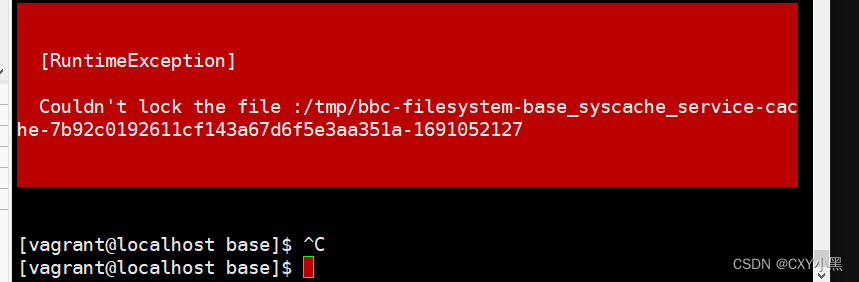
Couldn‘t lock the file :/tmp/bbc-filesystem-base_syscache_service
解决方案: 进去带这个目录,然后切换成root用户,将它删除...

vscode 通过mongoose 连接mongodb atlas
了解mongodb 的项目结构 1.代表集群名称 > 2.代表数据库名称>3.代表每个 collection名称 三者范围为从大到小的关系 (一对多)。每个集群有不同的连接地址、用户信息(Database Access)、ip配置信息(Network Acce…...

记录 Vue3 + Ts 类型使用
阅读时长: 10 分钟 本文内容:记录在 Vue3 中使用 ts 时的各种写法. 类型大小写 vue3 ts 项目中,类型一会儿大写一会儿小写。 怎么区分与基础类型使用? String、string、Number、number、Boolean、boolean … 在 js 中, 以 string 与 String…...
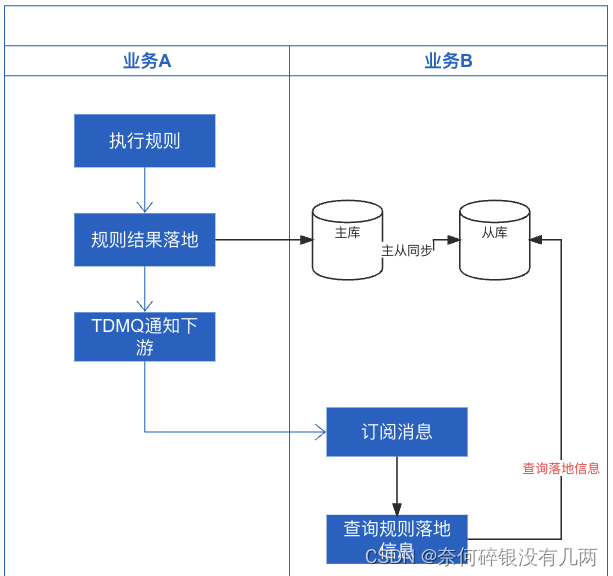
主从同步带来的业务问题
目录 一: 目前的业务问题二:如何平衡主从不同步和业务隔离?三:解决方案 一: 目前的业务问题 业务A会跑一些规则, 跑完会把规则结果信息落地(落地到主库), 然后会通过TDM…...

主动带宽控制工具
停机和带宽过度使用是任何组织都无法避免的两个问题。随着企业采用 BYOD 文化,通过网络的流量负载可能很重,导致网络拥塞并使网络容易受到网络攻击。为了解决这个问题,企业需要全面的监控策略来保护网络,当看似大量的流量进入网络…...

数据采集的方法有哪些?
近年来,国家和各大企业都在部署大数据战略。“大数据”这个词也越来越频繁地出现在我们的生活中。当我们在进行网上冲浪时,页面总会跳出我们想要搜索的相关产品或关联事物。大数据,似乎总是能够“算”出我们“心中所想”。那么,大…...

linux重新学习-纪录篇
前言: 正式学习linux的时候,除了那些命令之外,更多的是对于这个系统的重新认知。 linux的身世? 在上世纪90年代,那时候计算机非常的珍贵,配置也很一般般,系统也贵,所以没啥人用,在当…...
为机器人装“大脑” 谷歌发布RT-2大模型
大语言模型不仅能让应用变得更智能,还将让机器人学会举一反三。在谷歌发布RT-1大模型仅半年后,专用于机器人的RT-2大模型于近期面世,它能让机器人学习互联网上的文本和图像,并具备逻辑推理能力。 该模型为机器人智能带来显著升级…...
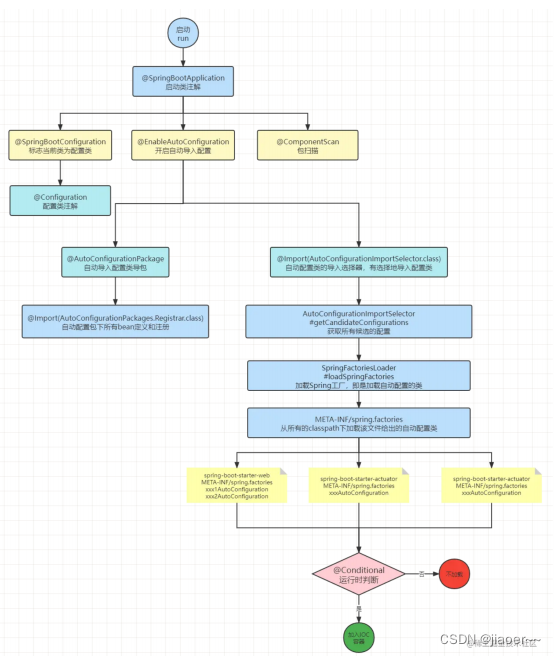
JavaEE 面试常见问题
一、常见的 ORM 框架有哪些? 1.Mybatis Mybatis 是一种典型的半自动的 ORM 框架,所谓的半自动,是因为还需要手动的写 SQL 语句,再由框架根据 SQL 及 传入数据来组装为要执行的 SQL 。其优点为: 1. 因为由程序员…...
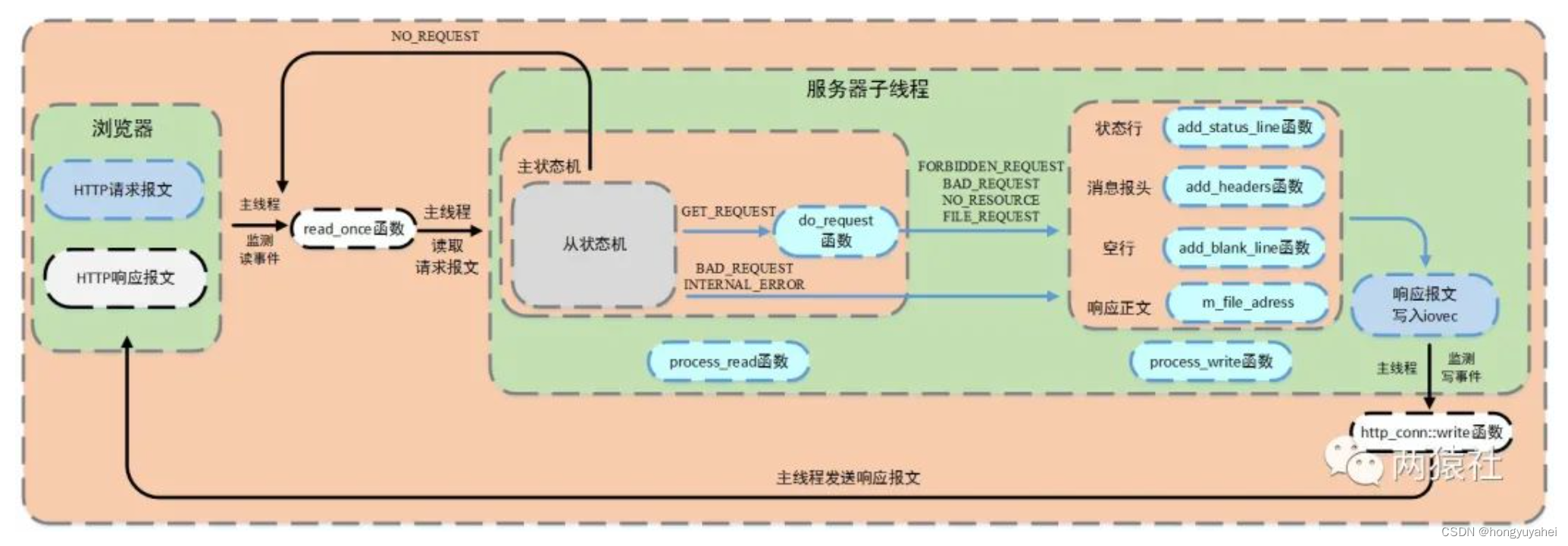
06 HTTP(下)
06 HTTP(下) 介绍服务器如何响应请求报文,并将该报文发送给浏览器端。介绍一些基础API,然后结合流程图和代码对服务器响应请求报文进行详解。 基础API部分,介绍stat、mmap、iovec、writev。 流程图部分,描…...
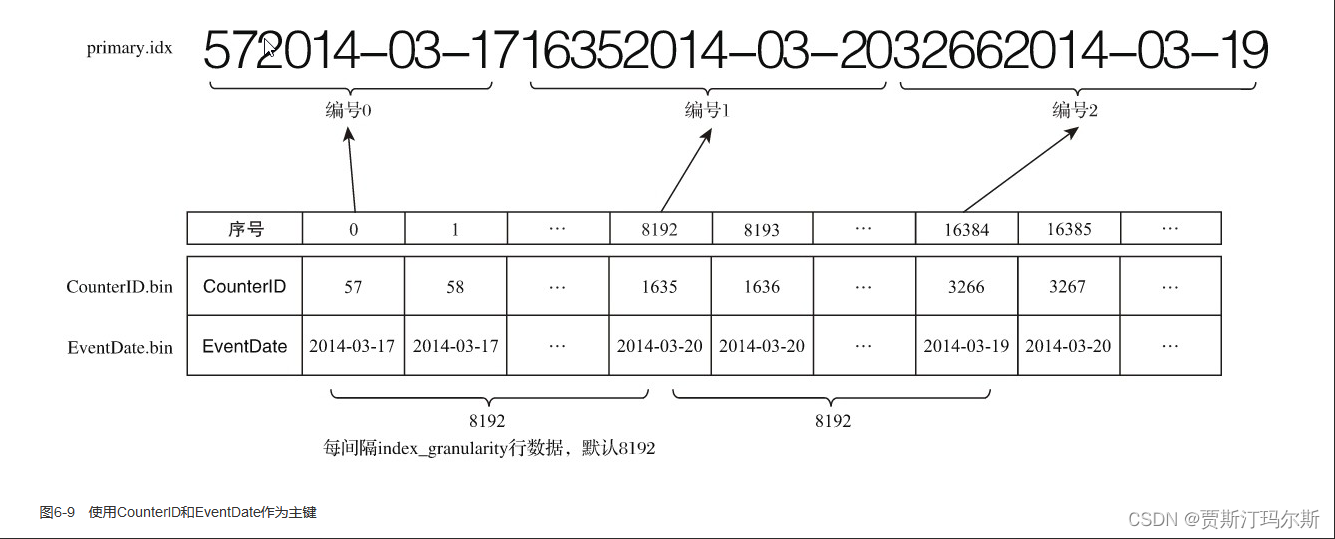
clickhouse调研报告2
由Distributed表发送分片数据 clickhouse分区目录合并 clickhouse副本协同流程 clickhouse索引查询逻辑 clickhouse一级索引生成逻辑(两主键) clickhouse的data目录下包含如下目录: [root@brfs-stress-01 201403_10_10_0]# ll /data01/clickhouse/data total 4 drwxr-x---…...

TensorRT学习笔记--基于TensorRT部署YoloV3, YoloV5和YoloV8
目录 1--完整项目 2--模型转换 3--编译项目 4--序列化模型 5--推理测试 1--完整项目 以下以 YoloV8 为例进行图片和视频的推理,完整项目地址如下:https://github.com/liujf69/TensorRT-Demo git clone https://github.com/liujf69/TensorRT-Demo.…...

原型链污染,nodejs逃逸例子
文章目录 原型链污染原型链污染原理原型链污染小例子 原型链污染题目解析第一题第二题 Nodejs沙箱逃逸方法一方法二 原型链污染 原型链污染原理 原型链 function test(){this.a test; } b new test;可以看到b在实例化为test对象以后,就可以输出test类中的属性a…...

nlohmann::json 中文乱码解决方案
// UTF8字符串转成GBK字符串 std::string U2G(const std::string& utf8) {int nwLen MultiByteToWideChar(CP_UTF8, 0, utf8.c_str(), -1, NULL, 0);wchar_t* pwBuf new wchar_t[nwLen 1];//加1用于截断字符串 memset(pwBuf, 0, nwLen * 2 2);MultiByteToWideChar(CP_U…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

游戏开发中常见的战斗数值英文缩写对照表
游戏开发中常见的战斗数值英文缩写对照表 基础属性(Basic Attributes) 缩写英文全称中文释义常见使用场景HPHit Points / Health Points生命值角色生存状态MPMana Points / Magic Points魔法值技能释放资源SPStamina Points体力值动作消耗资源APAction…...
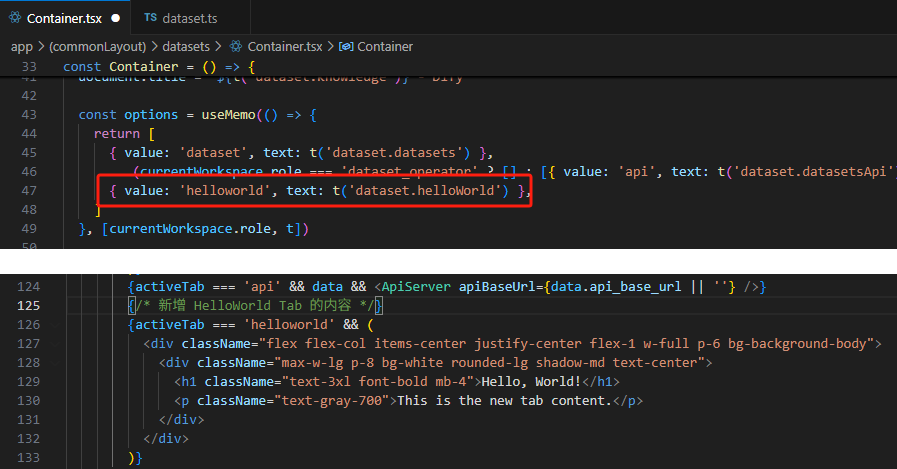
【技巧】dify前端源代码修改第一弹-增加tab页
回到目录 【技巧】dify前端源代码修改第一弹-增加tab页 尝试修改dify的前端源代码,在知识库增加一个tab页"HELLO WORLD",完成后的效果如下 [gif01] 1. 前端代码进入调试模式 参考 【部署】win10的wsl环境下启动dify的web前端服务 启动调试…...