石子合并一章通(环形石子合并,四边形不等式,GarsiaWachs算法)(内附封面)
[NOI1995] 石子合并
题目描述
在一个圆形操场的四周摆放 N N N 堆石子,现要将石子有次序地合并成一堆,规定每次只能选相邻的 2 2 2 堆合并成新的一堆,并将新的一堆的石子数,记为该次合并的得分。
试设计出一个算法,计算出将 N N N 堆石子合并成 1 1 1 堆的最小得分和最大得分。
输入格式
数据的第 1 1 1 行是正整数 N N N,表示有 N N N 堆石子。
第 2 2 2 行有 N N N 个整数,第 i i i 个整数 a i a_i ai 表示第 i i i 堆石子的个数。
输出格式
输出共 2 2 2 行,第 1 1 1 行为最小得分,第 2 2 2 行为最大得分。
样例 #1
样例输入 #1
4
4 5 9 4
样例输出 #1
43
54
提示
1 ≤ N ≤ 100 1\leq N\leq 100 1≤N≤100, 0 ≤ a i ≤ 20 0\leq a_i\leq 20 0≤ai≤20。
前置弱化版题目,石子合并(洛谷p1775)
做法1
单链复制,破环为链
本质上在时间复杂度没有变化,只是对于环形区间dp的一种做法
为什么长度为n的环可以看做长度为2n的链?
- 因为n堆石子会合并n-1次,就像并查集一样,最后总会刚好有两端是没有连接的,所以计算最大值可以这样算,然后从中选取长度为n且分数最大的一段链。
例: 对于序列 1 2 3 4 1\space2\space3\space4\space 1 2 3 4 ,复制为 1 2 3 4 1\space2\space3\space4\space 1 2 3 4 1 2 3 4 1\space2\space3\space4\space 1 2 3 4 ,前缀和求法不变
方程
d p _ m i n [ i ] [ j ] = m i n ( d p [ i ] [ j ] , d p [ i ] [ k ] + d p [ k + 1 ] [ j ] + s u m [ j ] − s u m [ i − 1 ] ) dp\_min[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+sum[j]-sum[i-1]) dp_min[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+sum[j]−sum[i−1])
d p _ m a x [ i ] [ j ] = m a x ( d p [ i ] [ j ] , d p [ i ] [ k ] + d p [ k + 1 ] [ j ] + s u m [ j ] − s u m [ i − 1 ] ) dp\_max[i][j]=max(dp[i][j],dp[i][k]+dp[k+1][j]+sum[j]-sum[i-1]) dp_max[i][j]=max(dp[i][j],dp[i][k]+dp[k+1][j]+sum[j]−sum[i−1])
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=303;
ll f_min[N][N],f_max[N][N],sum[N];
int main()
{int n;cin>>n;for(int i=1;i<=n;i++)scanf("%lld",&sum[i]),sum[i+n]=sum[i];memset(f_min,0x3f,sizeof f_min);//注意求f_min需要初始化for(int i=1;i<=2*n;i++){f_min[i][i]=0;//与自己合并价值为0sum[i]+=sum[i-1];//求前缀和,这是一种写法}for(int len=2;len<=n;len++)//dp部分,枚举区间长度{for(int i=1;i+len-1<=2*n;i++)//枚举左端点{int j=i+len-1;//右端点for(int k=i;k<j;k++)//枚举一个合适的中间点合并{f_max[i][j]=max(f_max[i][j],f_max[i][k]+f_max[k+1][j]+sum[j]-sum[i-1]);//求maxf_min[i][j]=min(f_min[i][j],f_min[i][k]+f_min[k+1][j]+sum[j]-sum[i-1]);//求min,他们的实现原理是相同的,方程也基本相同}}}ll ansmax=0,ansmin=0x3f3f3f3f3f3f3f3f;for(int i=1;i<=n;i++){ansmin=min(ansmin,f_min[i][i+n-1]);//寻找长度为n的答案区间ansmax=max(ansmax,f_max[i][i+n-1]);}printf("%lld\n",ansmin);printf("%lld",ansmax);return 0;
}
做法2
四边形不等式
这是一种对于部分区间动态规划的优化方法,本蒟蒻讲的不明白,建议去看这个
简单来说,四边形不等式长这样:(w代表区间价值)
对所有 i < i ′ < j < j ′ ,都有 w ( i , j ) + w ( i ′ , j ′ ) < = w ( i , j ′ ) + w ( i ′ , j ) 对所有i<i'<j<j',都有w(i,j)+w(i',j')<=w(i,j')+w(i',j) 对所有i<i′<j<j′,都有w(i,j)+w(i′,j′)<=w(i,j′)+w(i′,j)
若满足上述条件,则满足使用四边形不等式的条件
只有满足 w [ i ] [ j ] w[i][j] w[i][j]是关于 i 和 j 的二元函数时才能讨论单调性和四边形不等式的问题。
定理:
- 如果 w [ i , j ] w[i,j] w[i,j]满足四边形不等式和单调性,则用dp计算dp[][]的时间复杂度是 O ( n 2 ) O(n^2) O(n2)的
- 对于 d p _ m i n [ i ] [ j ] = m i n ( d p [ i ] [ j ] , d p [ i ] [ k ] + d p [ k + 1 ] [ j ] + s u m [ j ] − s u m [ i − 1 ] ) dp\_min[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+sum[j]-sum[i-1]) dp_min[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+sum[j]−sum[i−1]),如果 w [ i , j ] w[i,j] w[i,j]满足四边形不等式,那么 d p [ i ] [ j ] dp[i][j] dp[i][j]也满足四边形不等式。(dp_max同理)
- 记录 s [ i ] [ j ] s[i][j] s[i][j]为 d p [ i ] [ j ] dp[i][j] dp[i][j]取得最优值时的分割点,如果dp满足四边形不等式,那么 s [ i ] [ j − 1 ] < = s [ i ] [ j ] < = s [ i + 1 ] [ j ] s[i][j-1]<=s[i][j]<=s[i+1][j] s[i][j−1]<=s[i][j]<=s[i+1][j]
使用
看着原理很复杂,但对于求最小值的实现其实很简单,只需要把最后一层循环更改为 s [ i ] [ j − 1 ] < = k < = s [ i + 1 ] [ j ] s[i][j-1]<=k<=s[i+1][j] s[i][j−1]<=k<=s[i+1][j]即可
但是!求最大值不能用四边形不等式,
因为最大值不满足单调性,
但最大值有一个性质,
即总是在两个端点的最大者中取到。
为什么最大值从可以两个端点的最大者取得?
首先可以把最后一步看成两堆石子合并,倒数第二部看成三堆石子中的两堆合并,再与第三堆合并。
那三堆中哪两堆合并呢?
(用w[i]表示第i堆重量)
前两堆:w1=2w[1]+2w[2]+w[3]w1=2w[1]+2w[2]+w[3]
后两堆:w2=w[1]+2w[2]+2w[3]w2=w[1]+2w[2]+2w[3](自行推导)
所以应该将1号和3号中较大的一堆与第2堆合并,也就是把一堆合并得尽可能大,所以就有
因此对于最大值有以下方程
d p _ m a x = m a x ( d p _ m a x [ i ] [ j − 1 ] , d p _ m a x [ i + 1 ] [ j ] ) + s u m [ j ] − s u m [ i − 1 ] dp\_max=max(dp\_max[i][j-1],dp\_max[i+1][j])+sum[j]-sum[i-1] dp_max=max(dp_max[i][j−1],dp_max[i+1][j])+sum[j]−sum[i−1]
注意!求 d p _ m i n dp\_min dp_min时不能直接修改 d p _ m i n [ i ] [ j ] dp\_min[i][j] dp_min[i][j],因为在更改时会影响循环内的部分值
写法1
for(int len=2;len<=n;len++){for(int i=2*n-1;i>0;i--){//注意反推,存在f_min[i+1][j]int j=i+len-1;int tmp=INF,s_tmp=0;f_max[i][j]=max(f_max[i][j-1],f_max[i+1][j])+sum[j]-sum[i-1];for(int k=s_min[i][j-1];k<=s_min[i+1][j];k++){if(f_min[i][k]+f_min[k+1][j]+sum[j]-sum[i-1]<tmp){tmp=f_min[i][k]+f_min[k+1][j]+sum[j]-sum[i-1];s_tmp=k;}}s_min[i][j]=s_tmp;f_min[i][j]=tmp;}}
写法2
for(int i=n*2-1;i>0;i--){for(int j=i+1;j<=n*2;j++){//注意反推,存在f_min[i+1][j]int tmp=INF,s_tmp=0;f_max[i][j]=max(f_max[i][j-1],f_max[i+1][j])+sum[j]-sum[i-1];for(int k=s_min[i][j-1];k<=s_min[i+1][j];k++){if(f_min[i][k]+f_min[k+1][j]+sum[j]-sum[i-1]<tmp){tmp=f_min[i][k]+f_min[k+1][j]+sum[j]-sum[i-1];s_tmp=k;}}s_min[i][j]=s_tmp;f_min[i][j]=tmp;}}
完整AC CODE(同样两种写法,本质相同,只是循环有略微的差异)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=303;
const int INF=0x3f3f3f3f;
ll f_min[N][N],f_max[N][N],sum[N];
ll s_min[N][N];
int main()
{int n;cin>>n;for(int i=1;i<=n;i++){scanf("%lld",&sum[i]);sum[i+n]=sum[i];}memset(f_min,0x3f,sizeof f_min);for(int i=1;i<=2*n;i++){f_min[i][i]=0;sum[i]+=sum[i-1];s_min[i][i]=i;//s_max[i][i]=i;}for(int i=n*2-1;i>0;i--){//写法1for(int j=i+1;j<=n*2;j++){//注意反推,存在f_min[i+1][j]int tmp=INF,s_tmp=0;f_max[i][j]=max(f_max[i][j-1],f_max[i+1][j])+sum[j]-sum[i-1];for(int k=s_min[i][j-1];k<=s_min[i+1][j];k++){if(f_min[i][k]+f_min[k+1][j]+sum[j]-sum[i-1]<tmp){f_min[i][j]=f_min[i][k]+f_min[k+1][j]+sum[j]-sum[i-1];s_min[i][j]=k; }}s_min[i][j]=s_tmp;f_min[i][j]=tmp;}}/*for(int len=2;len<=n;len++){ //写法2for(int i=2*n-1;i>0;i--){//注意反推,存在f_min[i+1][j]int j=i+len-1;int tmp=INF,s_tmp=0;f_max[i][j]=max(f_max[i][j-1],f_max[i+1][j])+sum[j]-sum[i-1];for(int k=s_min[i][j-1];k<=s_min[i+1][j];k++){if(f_min[i][k]+f_min[k+1][j]+sum[j]-sum[i-1]<tmp){tmp=f_min[i][k]+f_min[k+1][j]+sum[j]-sum[i-1];s_tmp=k;}}s_min[i][j]=s_tmp;f_min[i][j]=tmp;}}*/ll ansmax=0,ansmin=0x3f3f3f3f3f3f3f3f;for(int i=1;i<=n;i++){ansmin=min(ansmin,f_min[i][i+n-1]);ansmax=max(ansmax,f_max[i][i+n-1]);}cout<<ansmin<<endl;cout<<ansmax<<endl;return 0;
}
做法3 GarsiaWachs
这个算法可以说专为石子合并所生,对本题来说这个算法就相当于大炮打蚊子,
经过平衡树优化后它的时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn)
使用这个算法解决的石子合并是这个(戳我直达洛谷p5565)
该算法的步骤如下:
- 假设存在 A [ 0 ] A[0] A[0]和 A [ n + 1 ] A[n+1] A[n+1],将它们的值设为无穷大。
- 从 1 1 1到 n n n,找到第一个 k k k使 A [ k − 1 ] < = A [ k + 1 ] A[k-1] <= A[k+1] A[k−1]<=A[k+1],保存这个 k k k。
- 定义一个临时变量 t e m p temp temp,使 t e m p = A [ k − 1 ] + A [ k ] temp = A[k-1] + A[k] temp=A[k−1]+A[k],同时 a n s = t e m p ans = temp ans=temp。
- 从 1 1 1到 k − 1 k-1 k−1,找到第一个 i i i 使 A [ i ] > t e m p A[i] > temp A[i]>temp,保存这个 i i i。
- 从表A 中同时删除 A [ k − 1 ] A [ k-1 ] A[k−1] 和 A [ k ] A[k] A[k]。
- 在 i i i 之后插入一个 t e m p temp temp。
- 重复步骤2到6共循环 n − 1 n-1 n−1次,最后 a n s ans ans即为答案。
这个算法可以帮助我们找到最小的合并次数,以使得石子合并的得分总和最小。
简单理解版:
因为合并 a , b , c a,b,c a,b,c有两种合并方式,价值分别为 a + 2 b + 2 c a+2b+2c a+2b+2c和 2 a + 2 b + c 2a+2b+c 2a+2b+c,因此我们只需要比较 a a a 和 c c c 即可,于是先合并 a < c a<c a<c的,完了之后如果还有剩就从右边开始合并 b c bc bc
合并 a b ab ab 的时候,合并之后插入从左边数第一个大于他的数的后面开始(原因本蒟蒻也不理解www)
具体的实现可以用邻接表或者vector,以下给出vector的做法
代码实现
#include<bits/stdc++.h>
using namespace std;
const int N=1e6;
const int INF=0x7f7f7f7f;
int a[N],n,tmp;
long long int ans=0;
vector<int> v;
void work(){int kk=v.size()-2,q=-1,tmp;//for(int k=0;k<v.size()-2;k++){//如果我们在A[0]到A[n-3]找不到A[k]<=A[k+2],那么k的值应该为n-2if(v[k]<=v[k+2]){kk=k;break;}}tmp=v[kk]+v[kk+1];for(int i=kk-1;i>=0;i--){//从右往左找第一个 if(v[i]>tmp){q=i;break;}}v.erase(v.begin()+kk);v.erase(v.begin()+kk);//删除元素v.insert(v.begin()+q+1,tmp);//因为是在后面插入,所以要+1ans+=tmp;//答案累加return;
}
int main(){scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%d",&a[i]);v.push_back(a[i]);}for(int t=1;t<=n-1;t++){work();}printf("%lld",ans);return 0;
}
ps: 这玩意看着简单打起来好多坑
完结撒花~~~ (终于写完了)
附封面
相关文章:
(内附封面))
石子合并一章通(环形石子合并,四边形不等式,GarsiaWachs算法)(内附封面)
[NOI1995] 石子合并 题目描述 在一个圆形操场的四周摆放 N N N 堆石子,现要将石子有次序地合并成一堆,规定每次只能选相邻的 2 2 2 堆合并成新的一堆,并将新的一堆的石子数,记为该次合并的得分。 试设计出一个算法,计算出将 …...
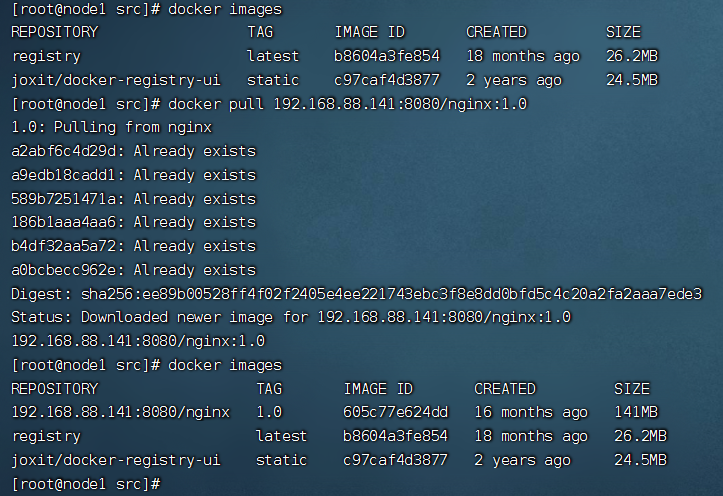
Docker快速入门笔记
Docker快速入门 前言 当今软件开发领域的一股热潮正在迅速兴起,它融合了便捷性、灵活性和可移植性,让开发者们欣喜若狂。它就是 Docker!无论你是一个初学者,还是一位经验丰富的开发者,都不能错过这个引领技术浪潮的工…...

【Excel】记录Match和Index函数的用法
最近一直用到的两个处理EXCEL表格数据的函数向大家介绍一下,写这篇博文的目的也是为了记录免得自己忘记了,嘻嘻。 先上百度的链接 Match函数的用法介绍:https://jingyan.baidu.com/article/2fb0ba40b4933941f3ec5f71.html 小结:…...
SolidUI社区-从开源社区角度思考苹果下架多款ChatGPT应用
文章目录 背景下架背景下架原因趋势SolidUI社区的未来规划结语如果成为贡献者 背景 随着文本生成图像的语言模型兴起,SolidUI想帮人们快速构建可视化工具,可视化内容包括2D,3D,3D场景,从而快速构三维数据演示场景。SolidUI 是一个创新的项目…...
插入排序讲解
插入排序(Insertion-Sort)一般也被称为直接插入排序。对于少量元素的排序,它是一个有效的算法。插入排序是一种最简单的排序方法,它的基本思想是将一个记录插入到已经排好序的有序表中,从而一个新的、记录数增1的有序表…...

杀疯了的ChatGPT——开启AI智能交流新纪元 「文末有彩蛋」
欢迎打开 ChatGPT 的新世纪大门 🌍 目录 😊 引言😎 ChatGPT 的高级之处1. 巨大的模型规模2. 广泛的知识覆盖3. 零样本学习4. 多语言支持5. 上下文感知对话 🤖 如何使用 ChatGPT1. 智能助手2. 个性化交互3. 语言学习伙伴4. 创造性写…...

web爬虫第五弹 - JS逆向入门(猿人学第一题)
0- 前言 爬虫是一门需要实战的学问。 而对于初学者来说,要想学好反爬,js逆向则是敲门砖。今天给大家带来一个js逆向入门实例,接下来我们一步一步来感受下入门的逆向是什么样的。该案例选自猿人学练习题。猿人学第一题 1- 拿到需求 进入页面…...

P5731 【深基5.习6】蛇形方阵
题目描述 给出一个不大于 9 9 9 的正整数 n n n,输出 n n n\times n nn 的蛇形方阵。 从左上角填上 1 1 1 开始,顺时针方向依次填入数字,如同样例所示。注意每个数字有都会占用 3 3 3 个字符,前面使用空格补齐。 输入格式…...
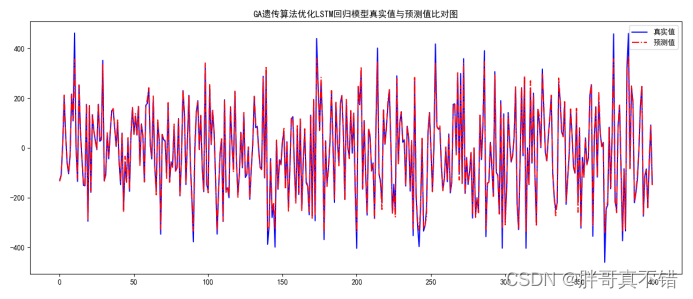
Python实现GA遗传算法优化循环神经网络回归模型(LSTM回归算法)项目实战
说明:这是一个机器学习实战项目(附带数据代码文档视频讲解),如需数据代码文档视频讲解可以直接到文章最后获取。 1.项目背景 遗传算法(Genetic Algorithm,GA)最早是由美国的 John holland于20世…...

ESD防静电监控系统在SMT产线中的应用案例
作为电子厂的关键制造环节之一,SMT(表面贴装技术)产线的效率和质量对企业的竞争力至关重要。为了提高生产线的管理效率和保障生产环境的质量,许多电子厂开始采用MES生产管理系统和ESD防静电监控系统的综合解决方案。 在SMT产线中安…...

Vue+Nodejs+Express+Minio 实现本地图片上传
安装Minio,Minio server和Minio client都要下载可以自定义安装目录 安装完成之后,可以将minio配置成环境变量方便使用 配置了环境变量启动命令式 minio server start,默认账号密码minioadmin和minioadmin,点击9000端口的这个链接,即可访问客户端 nodejs连接Minio,简易服务进…...
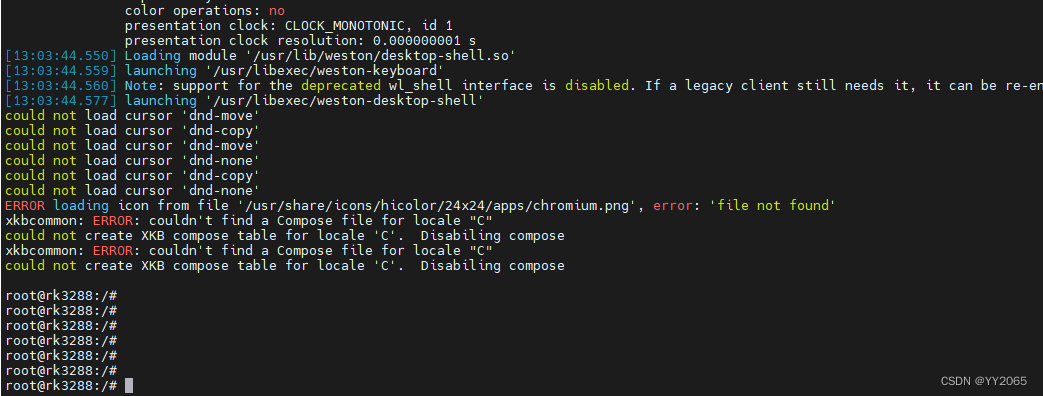
em3288 linux_4.19 第一次烧写无法进入内核的情况
1. 情况一: /DDR Version 1.11 20210818 In SRX Channel a: DDR3 400MHz Bus Width32 Col10 Bank8 Row15 CS1 Die Bus-Width16 Size1024MB Channel b: DDR3 400MHz Bus Width32 Col10 Bank8 Row15 CS1 Die Bus-Width16 Size1024MB OUT Boot1 Release Time: Jul 22 2…...

【Java多线程学习5】什么是悲观锁,什么是乐观锁?如何实现乐观锁、乐观锁存在哪些问题
【Java多线程学习5】什么是悲观锁,什么是乐观锁?如何实现乐观锁、乐观锁存在哪些问题 一、什么是悲观锁 概述 悲观锁总是假设最坏的情况,认为共享资源每次被访问的时候就会出现问题(比如共享数据被修改),所以每次在获取资源操作…...
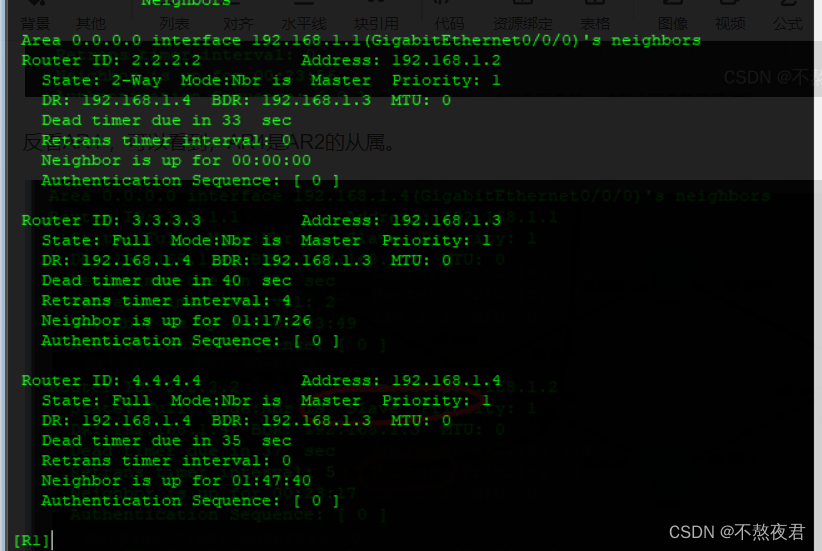
OSPF协议RIP协议+OSPF实验(eNSP)
本篇博客主要讲解单区域的ospf,多区域的仅作了解。 目录 一、OSPF路由协议概述 1.内部网关协议和外部网关协议 二、OSPF的应用环境 1.从以下几方面考虑OSPF的使用 2.OSPF的特点 三、OSPF重要基本概念 3.1,辨析邻居和邻接关系以及七种邻居状态 3…...
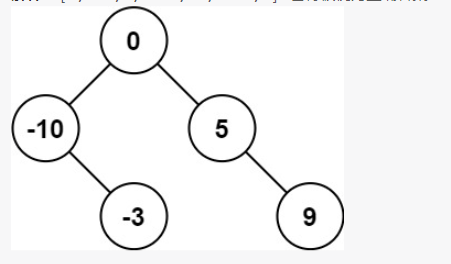
leetcode每日一练-第108题-将有序数组转换为二叉搜索树
一、思路 递归 二、解题方法 在给定中序遍历序列数组的情况下,每一个子树中的数字在数组中一定是连续的,因此可以通过数组下标范围确定子树包含的数字,下标范围记为 [left,right]。对于整个中序遍历序列,下标范围从 left0到 ri…...
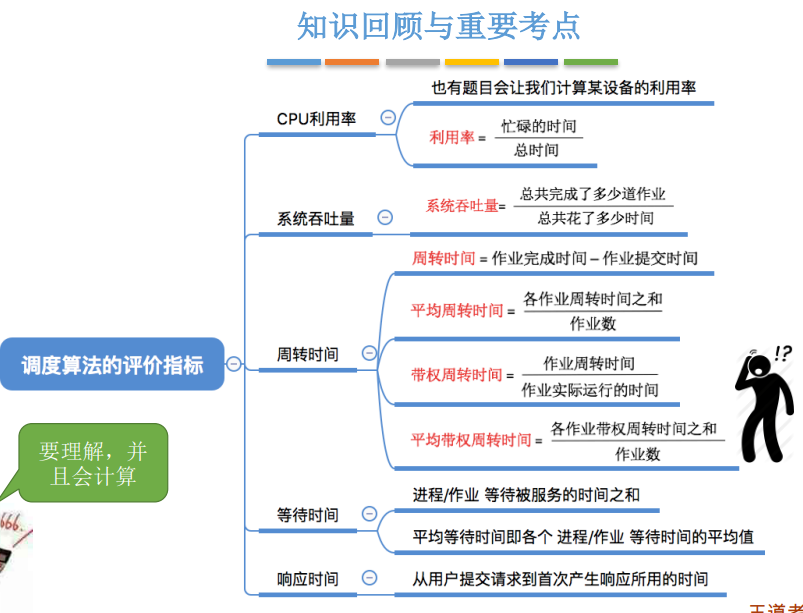
王道《操作系统》学习(二)—— 进程管理(二)
2.1 处理机调度的概念、层次 2.1.1 调度的基本概念 2.1.2 调度的三个层次 (1)高级调度(作业调度) (2)中级调度(内存调度) 补充知识:进程的挂起状态和七状态模型 &#x…...
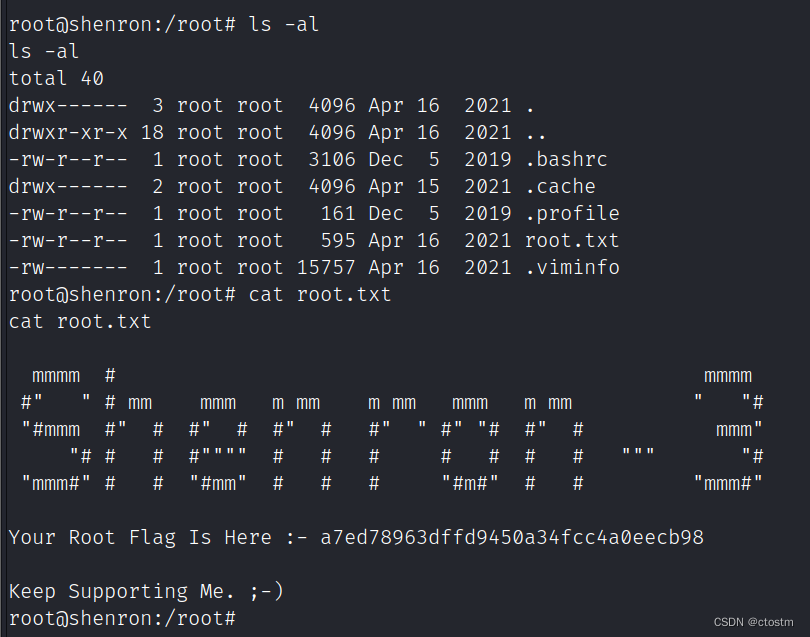
Vulnhub: shenron: 3靶机
kali:192.168.111.111 靶机:192.168.111.171 信息收集 端口扫描 nmap -A -sC -v -sV -T5 -p- --scripthttp-enum 192.168.111.171 修改hosts后访问目标80端口,发现是wordpress wpscan收集目标用户,爆破出密码:ilov…...
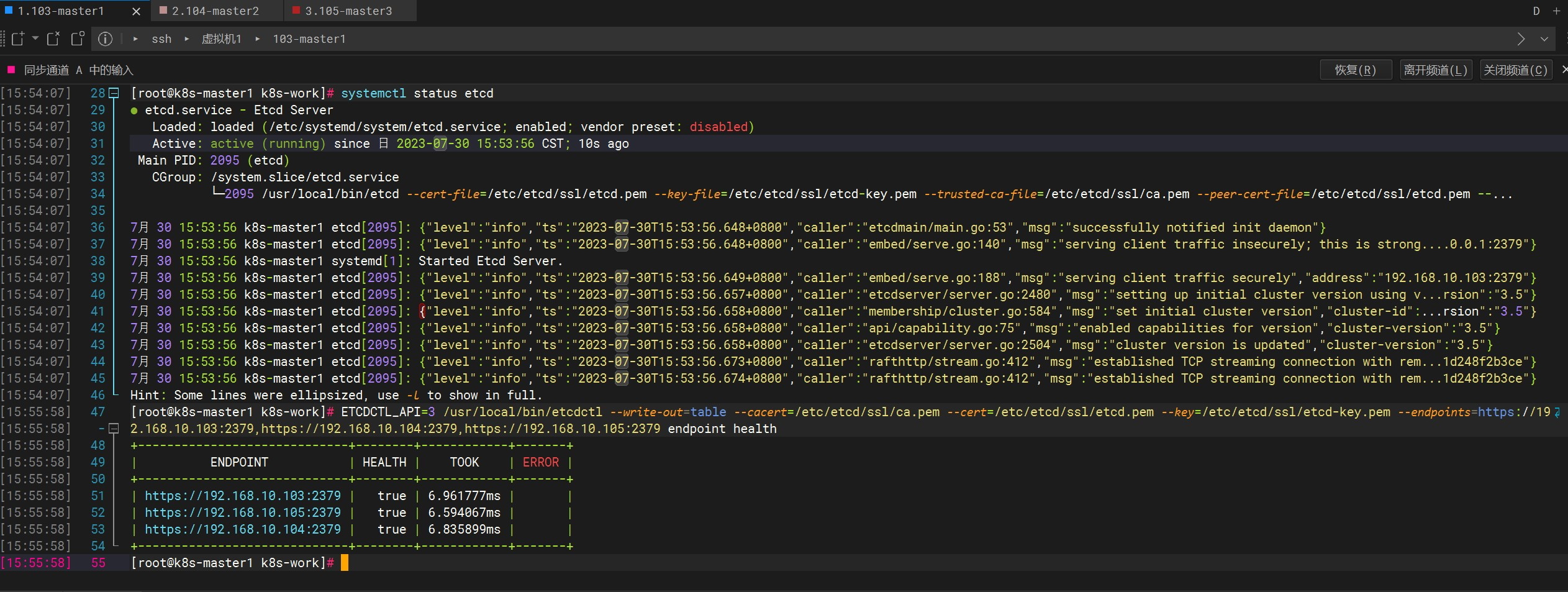
Kubernetes高可用集群二进制部署(二)ETCD集群部署
Kubernetes概述 使用kubeadm快速部署一个k8s集群 Kubernetes高可用集群二进制部署(一)主机准备和负载均衡器安装 Kubernetes高可用集群二进制部署(二)ETCD集群部署 Kubernetes高可用集群二进制部署(三)部署…...

mysql主从复制及原理
目录 主从复制原理实现主从复制 主从复制原理 主要基于MySQL二进制日志 主要包括三个线程(2个I/O线程,1个SQL线程) 1、MySQL将数据变化记录到二进制日志中; 2、Slave将MySQL的二进制日志拷贝到Slave的中继日志中; …...

MQTT服务器详细介绍:连接物联网的通信枢纽
随着物联网技术的不断发展,MQTT(Message Queuing Telemetry Transport)协议作为一种轻量级、可靠、灵活的通信协议,被广泛应用于物联网领域。在MQTT系统中,MQTT服务器扮演着重要的角色,作为连接物联网设备和…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...
