当前位置： 首页 > news >正文

HSRM各表

news 2026/2/9 17:24:07

文章目录

  • 表规则
  • 接口种类
  • 服务与网关路由
  • 菜单
  • 一、采购申请
      • 1、采购申请—查询
      • 2、采购申请-操作记录
  • 二、采购申请跟踪报表
      • 1、采购申请跟踪报表—列表查询
  • 三、寻源
      • 1、寻源大厅—列表查询
      • 2、寻源大厅—询价单明细
      • 3、寻源大厅—物料明细
      • 4、寻源大厅—供应商列表
      • 5、寻源模板—列表查询
  • 四、订单维护
      • 1、订单维护-列表查询
      • 2、订单维护—详情
      • 3、订单行
  • 五、采购方订单汇总

    相关文章：

    HSRM各表

    文章目录 表规则接口种类服务与网关路由菜单一、采购申请1、采购申请—查询2、采购申请-操作记录二、采购申请跟踪报表1、采购申请跟踪报表—列表查询三、寻源1、寻源大厅—列表查询2、寻源大厅—询价单明细3、寻源大厅—物料明细4、寻源大厅—供应商列表5、寻源模板—列表查询…...

    编程日记 2023/8/4 6:55:21

    Ansible自动化运维工具 —— Playbook 剧本

    playbooks 本身由以下各部分组成 （1）Tasks：任务，即通过 task 调用 ansible 的模板将多个操作组织在一个 playbook 中运行 （2）Variables：变量 （3）Templates：模…...

    编程日记 2023/8/4 6:54:19

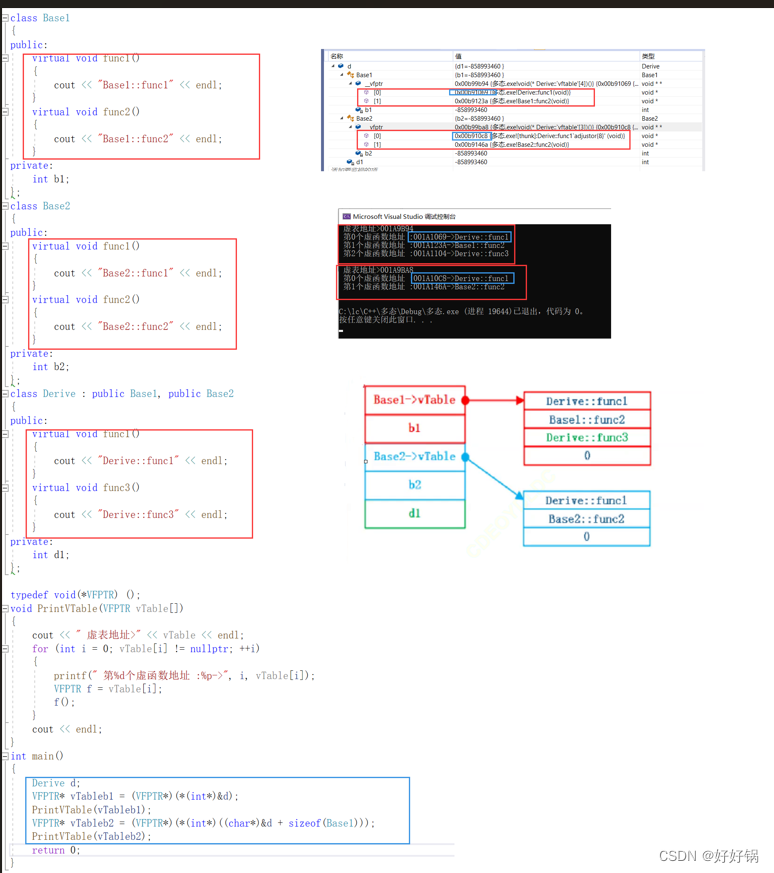
    第二章：多态

    系列文章目录 文章目录 系列文章目录前言多态的概念概念 多态的定义及实现多态的构成条件虚函数虚函数的重写C11 override 和 final重载、覆盖(重写)、隐藏(重定义)的对比 抽象类概念接口继承和实现继承 多态的原理虚函数表多态的原理动态绑定与静态绑定 单继承和多继承关系的虚…...

    编程日记 2023/8/4 6:53:18

    C++面向对象设计基础

    一般类、&、const、模板、友元函数、操作符重载基本用法及实现 complex.h #ifndef COMPLEX_H #define COMPLEX_H #include<ostream> using namespace std;template<typename T> class Complex{public:Complex():re(0),img(0){}// 为什么构造函数不能传引用&a…...

    编程日记 2023/8/4 6:52:17

    Linux定时运行sh脚本，如果sh文件已经在运行，则忽略本次运行

    需求来源 我需要linux的crontab定期每10分钟运行lan.sh脚本。但由于lan.sh运行需要较长时间&#xff0c;有时超过10分钟。这样会导致系统多次运行lan.sh脚本&#xff0c;引发运行堆积&#xff0c;导致一些非必要的错误。 解决方法 解决方法是写一个脚本&#xff0c;如果lan.…...

    编程日记 2023/8/4 6:51:15

    SpringBoot项目中的web安全防护

    最近这个月公司对项目进行了几次安全性扫描&#xff0c;然后扫描出来了一些安全漏洞&#xff0c;所以最近也一直在修复各种安全漏洞&#xff0c;还有就是最近在备考软考高级系统架构设计师&#xff0c;也刚好复习到了网络安全这一个章节&#xff0c;顺便将最近修复的安全漏洞总…...

    编程日记 2023/8/4 6:50:12

    stm32和python串口数据收发

    1-1 串口发送端&#xff08;stm32&#xff09; 1字符串发送 void USART_SendData(USART_TypeDef* USARTx, uint16_t Data) {/* Check the parameters */assert_param(IS_USART_ALL_PERIPH(USARTx));assert_param(IS_USART_DATA(Data)); /* Transmit Data */USARTx->DR (D…...

    编程日记 2023/8/4 6:49:11

    无涯教程-jQuery - Dropable移动函数

    Drop-able 功能可与JqueryUI中的交互一起使用。此功能可在任何DOM元素上启用可放置功能。 Drop able - 语法 $( "#droppable" ).droppable(); Drop able - 示例 以下是一个简单的示例&#xff0c;显示了drop-able的用法- <html><head><title>…...

    编程日记 2023/8/4 6:48:10

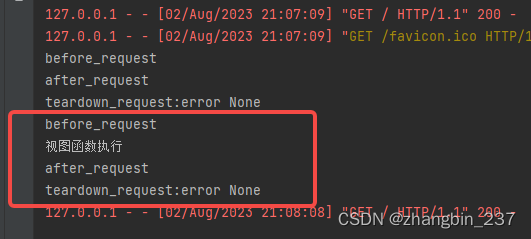
    【Python】Web学习笔记_flask(4)——钩子函数

    钩子函数可以用来注册在请求处理的不同阶段执行出 Flask的请求钩子指的是在执行视图函数前后执行的一些函数&#xff0c; 之前是有4种&#xff0c;但是 before_first_request已经被删除了&#xff0c;使用时会报错 before_request&#xff1a;在每次请求前执行&#xff0c;…...

    编程日记 2023/8/4 6:47:09

    JavaScript 原型链解析，宏任务和微任务

    目录 什么是原型链&#xff1f; 原型与构造函数 原型链的工作原理 实例&#xff1a;理解原型链 宏任务&#xff08;Macro Task&#xff09; 微任务&#xff08;Micro Task&#xff09; 什么是原型链&#xff1f; JavaScript 是一门基于原型的语言&#xff0c;而原型链是…...

    编程日记 2023/8/4 6:46:07

    05|Oracle学习（UNIQUE约束）

    1. UNIQUE约束介绍 也叫&#xff1a;唯一键约束&#xff0c;用于限定数据表中字段值的唯一性。 1.1 UNIQUE和primary key区别&#xff1a; 主键/联合主键每张表中只有一个。UNIQUE约束可以在一张表中&#xff0c;多个字段中存在。例如&#xff1a;学生的电话、身份证号都是…...

    编程日记 2023/8/4 6:45:06

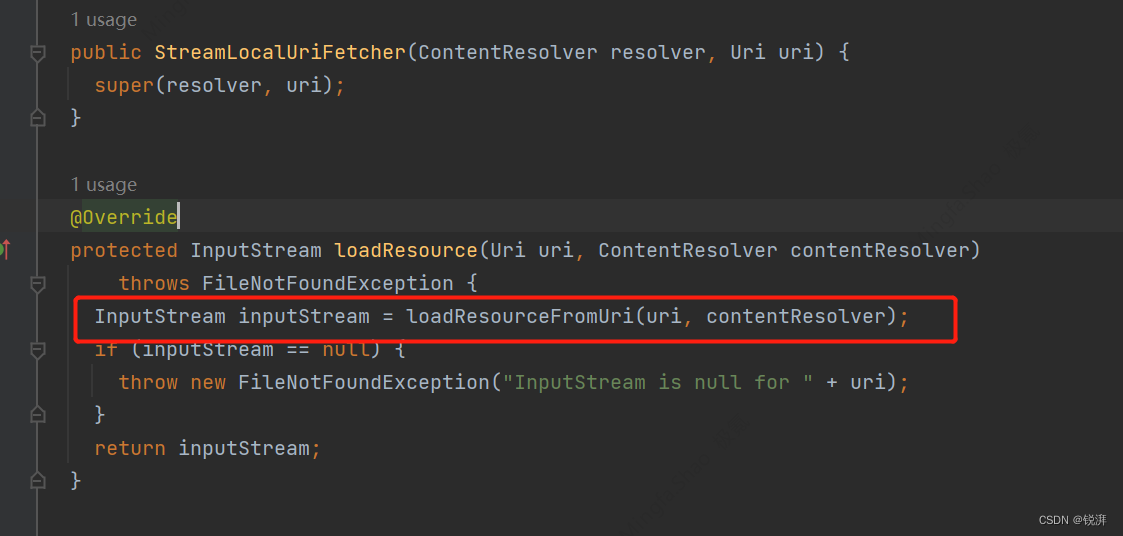
    glide加载content://com.android.contacts图片源码粗略梳理

    获取链路是这样的&#xff1b; UriLoader类里定义了协议头&#xff1a; 里面有个内部类StreamFactory&#xff1a; 通过StreamLocalUriFetcher类的loadResource方法获取InputStream然后把流转换成为图片&#xff1b; 在这里作个草稿笔记给自己看...

    编程日记 2023/8/4 6:44:03

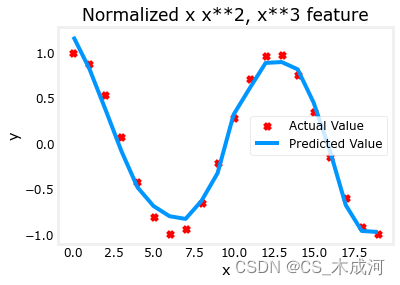
    【机器学习】Feature Engineering and Polynomial Regression

    Feature Engineering and Polynomial Regression 1. 多项式特征2. 选择特征3. 缩放特征4. 复杂函数附录 首先&#xff0c;导入所需的库&#xff1a; import numpy as np import matplotlib.pyplot as plt from lab_utils_multi import zscore_normalize_features, run_gradien…...

    编程日记 2023/8/4 6:43:02

    Rust- 变量绑定

    In Rust, you bind values to a variable name using the let keyword. This is often referred to as “variable binding” because it’s like binding a name to a value. Here’s a simple example: let x 5;In this example, x is bound to the value 5. By default, …...

    编程日记 2023/8/4 6:41:58

    向“数”而“深”，联想凌拓的“破局求变”底气何来？

    前言&#xff1a;要赢得更多机遇&#xff0c;“破局求变”尤为重要。 【全球存储观察 &#xff5c; 热点关注】2019年2月25日&#xff0c;承袭联想集团与NetApp的“双基因”&#xff0c;联想凌拓正式成立。历经四年多的发展&#xff0c;联想凌拓已成为中国企业级数据管理领域的…...

    编程日记 2023/8/4 6:40:57

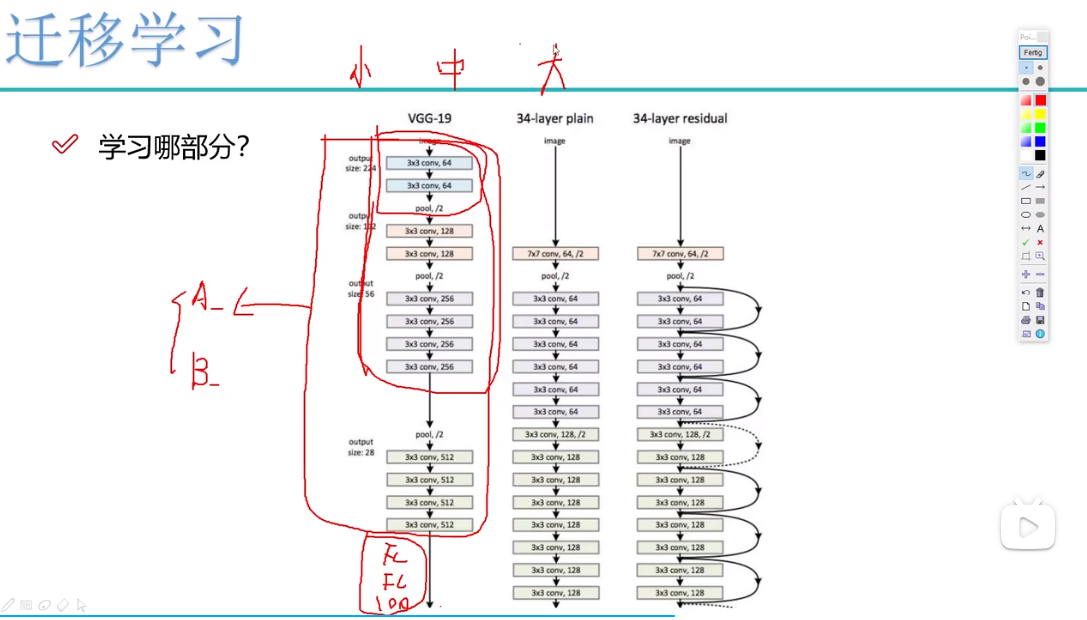
    pytorch实战-图像分类（二）（模型训练及验证）（基于迁移学习（理解+代码））

    目录 1.迁移学习概念 2.数据预处理 3.训练模型&#xff08;基于迁移学习&#xff09; 3.1选择网络&#xff0c;这里用resnet 3.2如果用GPU训练&#xff0c;需要加入以下代码 3.3卷积层冻结模块 3.4加载resnet152模 3.5解释initialize_model函数 3.6迁移学习网络搭建 3.…...

    编程日记 2023/8/4 6:39:56

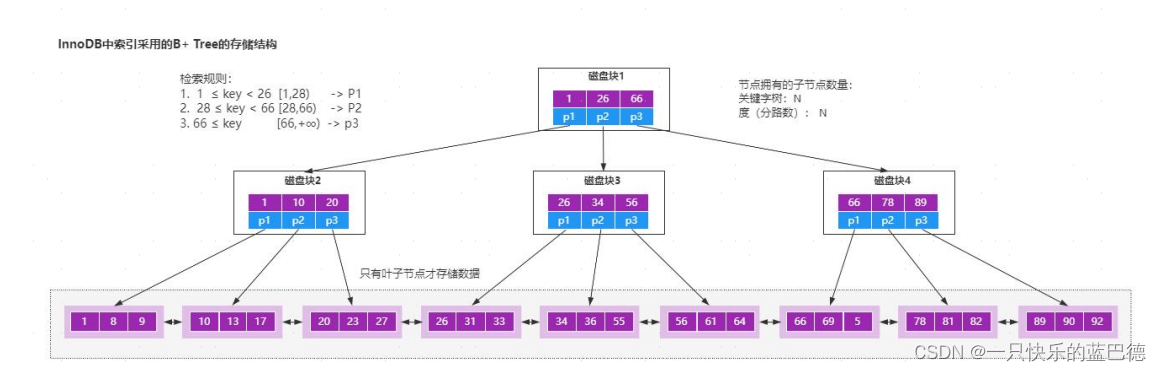
    b 树和 b+树的理解

    项目场景&#xff1a; 图灵奖获得者&#xff08;Niklaus Wirth &#xff09;说过&#xff1a; 程序 数据结构 算法&#xff0c; 也就说我们无时无刻 都在和数据结构打交道。 只是作为 Java 开发&#xff0c;由于技术体系的成熟度较高&#xff0c;使得大部分人认为&#xff1…...

    编程日记 2023/8/4 6:38:55

    正则表达式 —— Awk

    Awk awk&#xff1a;文本三剑客之一&#xff0c;是功能最强大的文本工具 awk也是按行来进行操作&#xff0c;对行操作完之后&#xff0c;可以根据指定命令来对行取列 awk的分隔符&#xff0c;默认分隔符是空格或tab键&#xff0c;多个空格会压缩成一个 awk的用法 awk的格式…...

    编程日记 2023/8/4 6:37:53

    国芯新作 | 四核Cortex-A53@1.4GHz，仅168元起？含税？哇！！！

    创龙科技SOM-TLT507是一款基于全志科技T507-H处理器设计的4核ARM Cortex-A53全国产工业核心板&#xff0c;主频高达1.416GHz。核心板CPU、ROM、RAM、电源、晶振等所有元器件均采用国产工业级方案&#xff0c;国产化率100%。 核心板通过邮票孔连接方式引出MIPI CSI、HDMI OUT、…...

    编程日记 2023/8/4 6:36:52

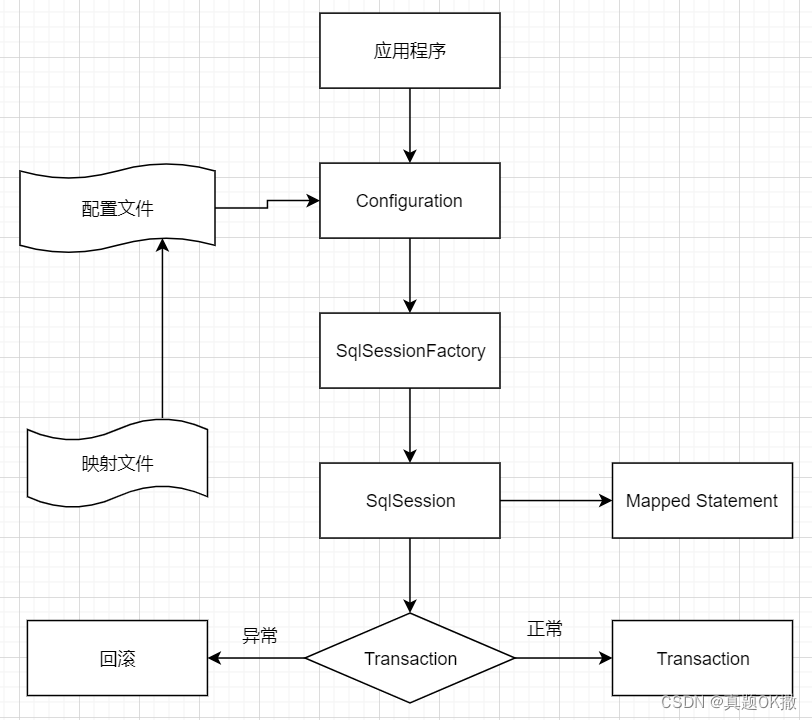
    【MyBatis】 框架原理

    目录 10.3【MyBatis】 框架原理 10.3.1 【MyBatis】 整体架构 10.3.2 【MyBatis】 运行原理 10.4 【MyBatis】 核心组件的生命周期 10.4.1 SqlSessionFactoryBuilder 10.4.2 SqlSessionFactory 10.4.3 SqlSession 10.4.4 Mapper Instances 与 Hibernate 框架相比&#…...

    编程日记 2023/8/4 6:35:51

    测试微信模版消息推送

    进入“开发接口管理”--“公众平台测试账号”&#xff0c;无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息&#xff1a; 关注测试号&#xff1a;扫二维码关注测试号。 发送模版消息&#xff1a; import requests da…...

    编程新知 2026/2/8 4:37:13

    渲染学进阶内容——模型

    最近在写模组的时候发现渲染器里面离不开模型的定义，在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容，其实不管是方块还是方块实体，都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器，用于动态创…...

    编程新知 2025/11/25 22:59:17

    深入解析C++中的extern关键字：跨文件共享变量与函数的终极指南

    &#x1f680; C extern 关键字深度解析&#xff1a;跨文件编程的终极指南 &#x1f4c5; 更新时间&#xff1a;2025年6月5日 &#x1f3f7;️ 标签&#xff1a;C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言&#x1f525;一、extern 是什么&#xff1f;&…...

    编程新知 2026/2/1 6:50:07

    C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。

    1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj&#xff0c;再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

    编程新知 2026/2/5 4:21:48

    分布式增量爬虫实现方案

    之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面&#xff0c;避免重复抓取&#xff0c;以节省资源和时间。 在分布式环境下&#xff0c;增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路&#xff1a;将增量判…...

    编程新知 2026/2/6 1:18:56

    站群服务器的应用场景都有哪些？

    站群服务器主要是为了多个网站的托管和管理所设计的&#xff0c;可以通过集中管理和高效资源的分配&#xff0c;来支持多个独立的网站同时运行&#xff0c;让每一个网站都可以分配到独立的IP地址&#xff0c;避免出现IP关联的风险&#xff0c;用户还可以通过控制面板进行管理功…...

    编程新知 2025/9/1 19:01:24

    [大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.

    ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #&#xff1a…...

    编程新知 2026/1/31 4:37:53

    android RelativeLayout布局

    <?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

    编程新知 2026/2/6 13:49:41

    【Linux】自动化构建-Make/Makefile

    前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具&#xff1a;make/makfile 1.背景 在一个工程中源文件不计其数&#xff0c;其按类型、功能、模块分别放在若干个目录中&#xff0c;mak…...

    编程新知 2026/2/4 16:04:21

    Python网页自动化Selenium中文文档

    1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API&#xff0c;让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API&#xff0c;你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

    编程新知 2026/1/23 18:15:21