leetcode 738. 单调递增的数字
2023.8.4
这题用暴力法会超时,我就没试了,采用了个挺巧的方法,为了方便需要先将整数n转换为字符串的形式,然后从后向前遍历,当两个数字非递增时,将前一个数字--,后一个数字的位置记录在index中,之后需要将这个index以后的数字全赋为9。 为了防止将不需要赋9的地方赋9,index需要初始化为超出这个字符串数组的索引,我初始化为一个最大整型值INT_MAX。最后的结果记得转回整数形式。 代码细节如下:
class Solution {
public:int monotoneIncreasingDigits(int n) {string str = to_string(n);//为了防止将不需要赋9的位置赋9int index = INT_MAX; for(int i=str.size()-1; i>0; i--){if(str[i] < str[i-1]){str[i-1]--;index = i;}}for(int i=index; i<str.size(); i++){str[i] = '9';}return stoi(str);}
};相关文章:

leetcode 738. 单调递增的数字
2023.8.4 这题用暴力法会超时,我就没试了,采用了个挺巧的方法,为了方便需要先将整数n转换为字符串的形式,然后从后向前遍历,当两个数字非递增时,将前一个数字--,后一个数字的位置记录在index中&…...
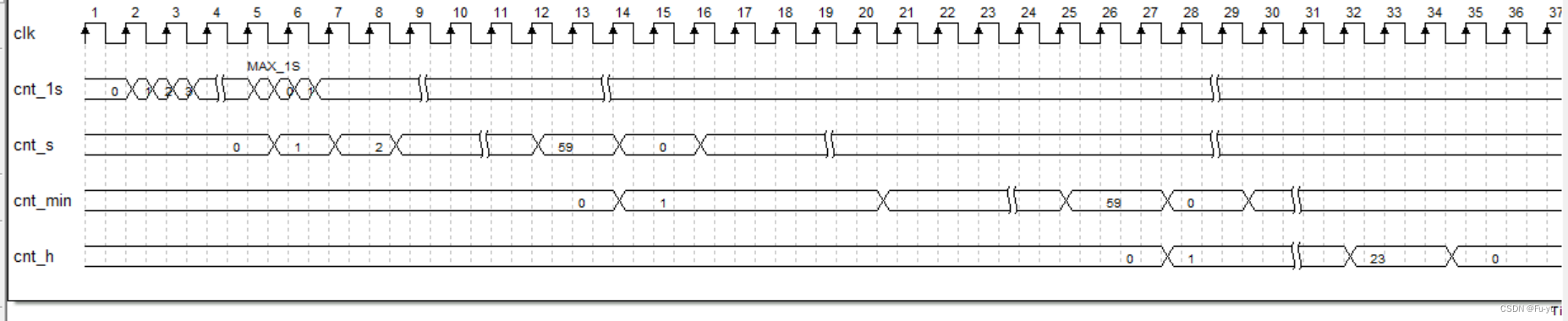
FPGA项目设计:数字时钟
项目要求: 设计一个数字时钟,数码管前两位显示小时,数码管中间两位显示分钟,数码管后面两位显示秒。 项目设计: 系统框架图: 计数模块时序图: 代码实现: 计数模块: /…...

科技云报道:向量数据库:AI时代的下一个热点
科技云报道原创。 最近,又一个概念火了——向量数据库。 随着大模型带来的应用需求提升,4月以来多家海外知名向量数据库创业企业传出融资喜讯。 4月28日,向量数据库平台Pinecone宣布获得1亿美元(约7亿元)B轮融资&am…...

【更新】119所院校考研重点勾画更新预告!
截至目前,我已经发布了47篇不同院校的择校分析。发布了87套名校信号考研真题以及119所不同院校的考研知识点重点勾画。 另外为了更好服务已经报名的同学,24梦马全程班也到了收尾的阶段。即将封班!需要报名的同学抓紧啦! 去年开始…...
LRU算法(哈希链表法))
【Leetcode】(自食用)LRU算法(哈希链表法)
step by step. 题目: 请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。 实现 LRUCache 类: LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存int get(int key) 如果关键字 key 存在于缓存中,则返回关键…...
搜索引擎获取页面内容)
robots.txt 如何禁止蜘蛛(百度,360,搜狗,谷歌)搜索引擎获取页面内容
什么是蜘蛛抓取 搜索引擎使用spider程序自动访问互联网上的网页并获取网页信息。spider在访问一个网站时,会首先会检查该网站的根域下是否有一个叫做robots.txt的纯文本文件。您可以在您的网站中创建一个纯文本文件robots.txt,在文件中声明该网站中不想…...
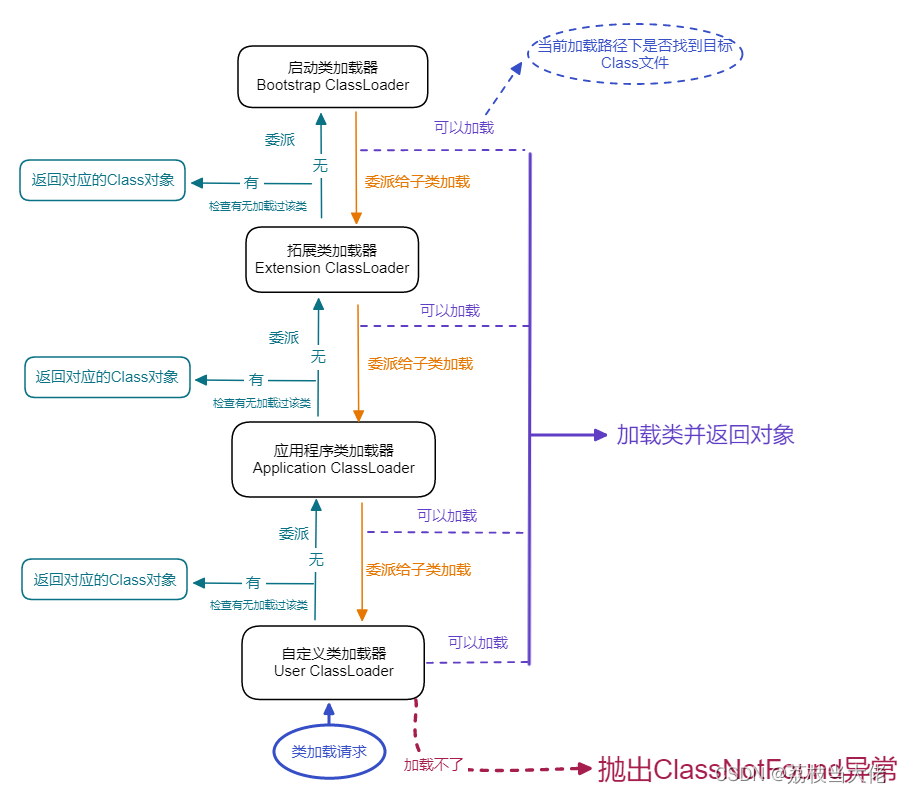
JVM 学习—— 类加载机制
前言 在上一篇文章中,荔枝梳理了有关Java中JVM体系架构的相关知识,其中涉及到的有关Java类加载机制的相关知识并没有过多描述。那么在这篇文章中,荔枝会详细梳理一下有关JVM的类加载机制和双亲委派模型的知识,希望能够帮助到有需要…...

C#实现int类型和字节流的相互在转化
通过TCP协议进行数据传输时,需要将所有传输的内容转为字节流,这里就用到了将int型的数据转为字节流的。代码如下: public static byte[] BytesConvertToInt(int vel) {byte[] hex new byte[4];hex[3] (byte)(vel >> 24) & 0xff)…...

Centos设置固定IP地址,外网访问
查看网络信息 一般会看到enp0s3的网络配置 ip address切换至网络配置路径 cd /etc/sysconfig/network-scripts/编辑配置 vi ifcfg-enp0s3 编辑配置 主要修改 静态ip:BOOTPROTOdhcp --> OOTPROTOstaticDNS(訪問外網):DNS1114.114.114.114本机ip: 192.168.70.121子网掩码…...
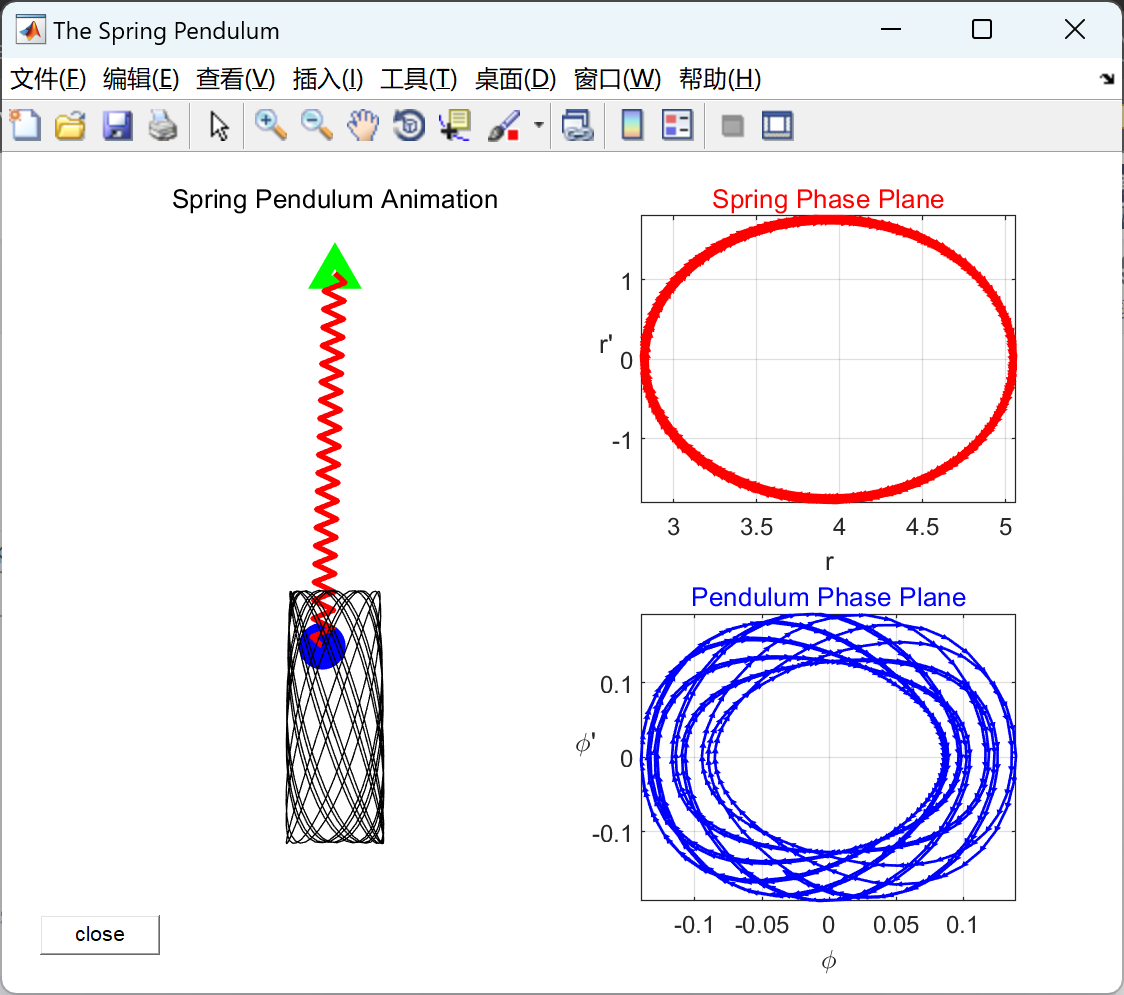
非线性弹簧摆的仿真(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

css实现文字颜色渐变+阴影
效果 代码 <div class"top"><div class"top-text" text"总经理驾驶舱">总经理驾驶舱</div> </div><style lang"scss" scoped>.top{width: 100%;text-align: center;height: 80px;line-height: 80px;fo…...

C++学习笔记总结练习:关联容器
关联容器 0 关联容器概述 关联容器与顺序容器的区别 关联容器和顺序容器有着根本不同。关联容器中的元素是按关键字来把偶才能和访问的。书序容器中的元素是按他们在容器中的位置来顺序保存和访问的。 两个基础类型 map:键值对key-value。关键字是索引,值表示与…...
)
TypeScript技能总结(二)
typescript是js的超集,目前很多前端框架都开始使用它来作为项目的维护管理的工具,还在不断地更新,添加新功能中,我们学习它,才能更好的在的项目中运用它,发挥它的最大功效 //readonly 只能修饰属性&#x…...

整理一些Postgresql工作中常用面试中会问的问题---Postgresql面试题001
1.什么是Postgresql TOAST? TOAST (The Oversized-Attribute Storage Technique,超大尺寸字段存储技术)主要用于存储大字段的值。 PostgreSQL 页面(page)大小是固定的(通常为8KB),且不允许tuples跨多个页面存储。因此不能存储非常大的字段值。为了克服这个限制,大字段…...
Xposed回发android.os.NetworkOnMainThreadException修复
最近用xposed进行hook回发的时候,又出现了新的问题; android.os.NetworkOnMainThreadException; 在Android4.0以后,写在主线程(就是Activity)中的HTTP请求,运行时都会报错,这是因为…...
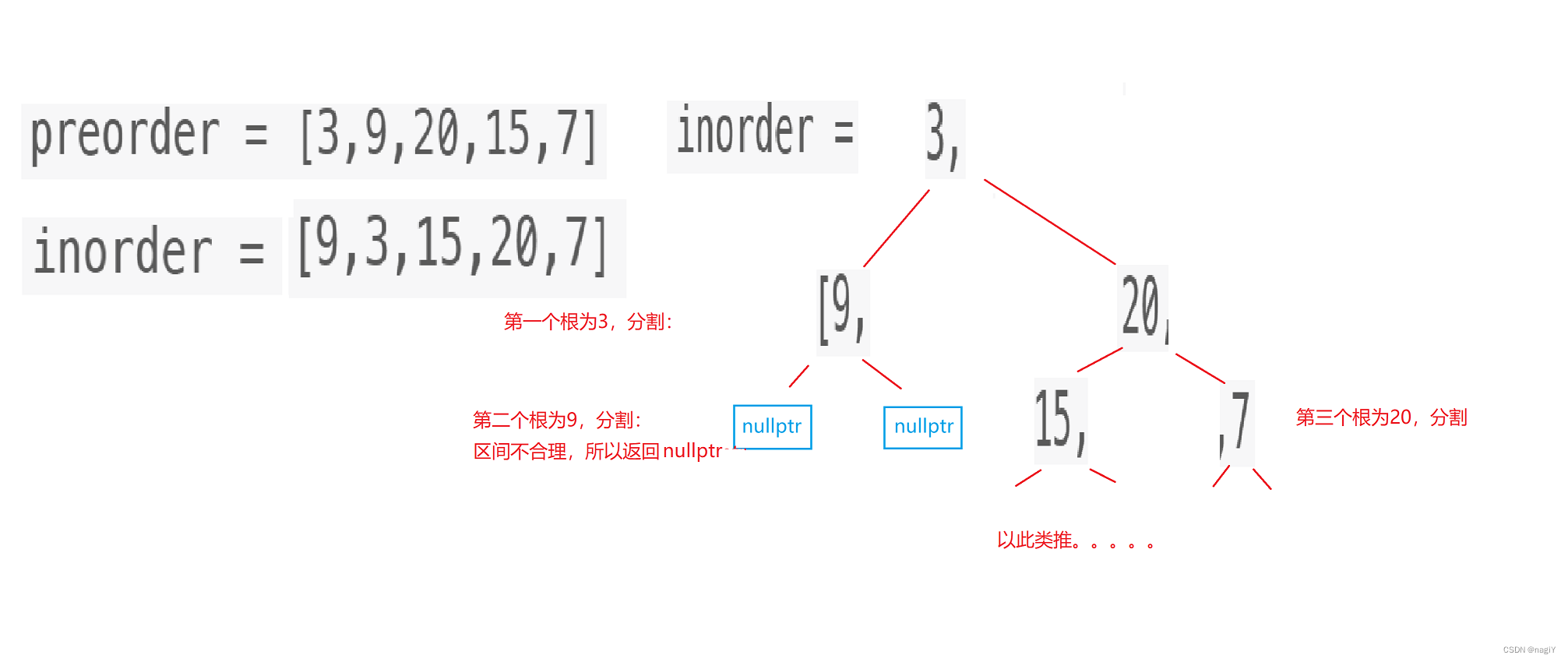
【Leetcode】二叉树的最近公共祖先,二叉搜索树转换成排好序的双向链表,前序遍历与中序遍历构造二叉树
一.二叉树的最近公共祖先 链接 二叉树的最近公共祖先 题目再现 『Ⅰ』思路一:转换成相交链表问题 观察上图,节点1和节点4的最近公共祖先是3,这是不是很像相交链表的问题,关于相交链表,曾经我在另一篇文章里写到过&a…...

途乐证券|互联金融概念爆发,安硕信息“20cm”涨停,高伟达等大涨
互联金融概念4日盘中强势拉升,截至发稿,安硕信息“20cm”涨停,高伟达、卓创资讯、慧博云通涨超12%,恒银科技、极点软件亦涨停,指南针涨超9%,金证股份涨逾7%。 高伟达昨日在投资者互动平台表明,公…...
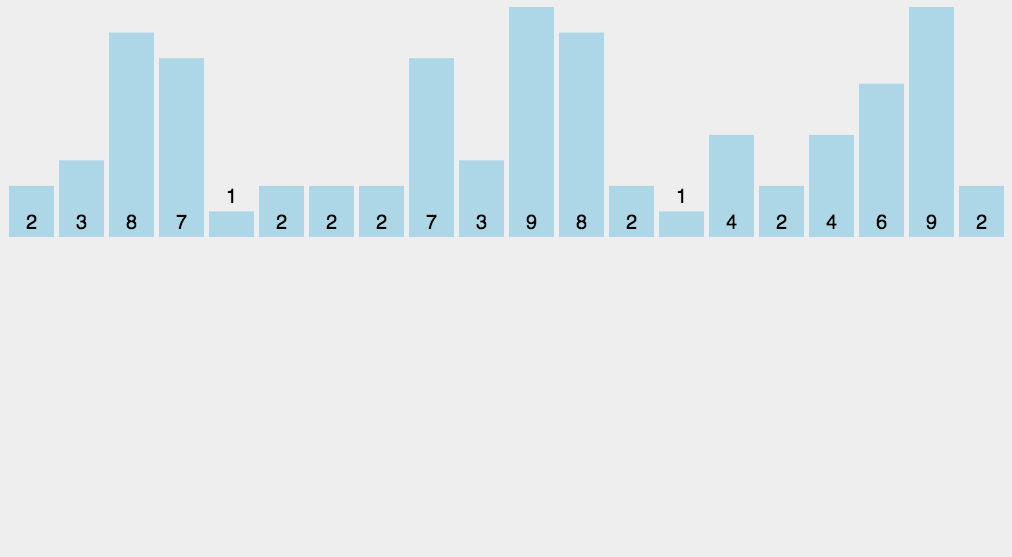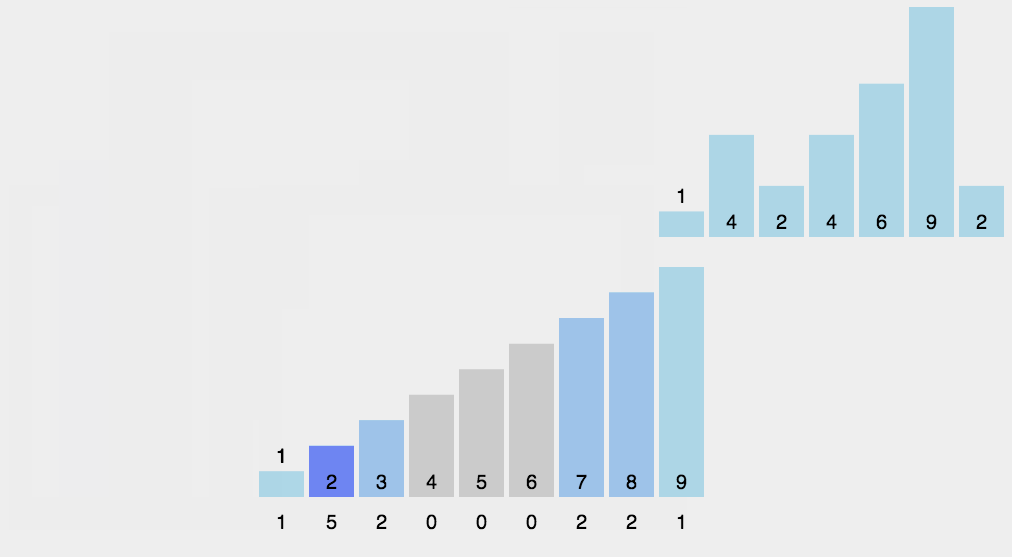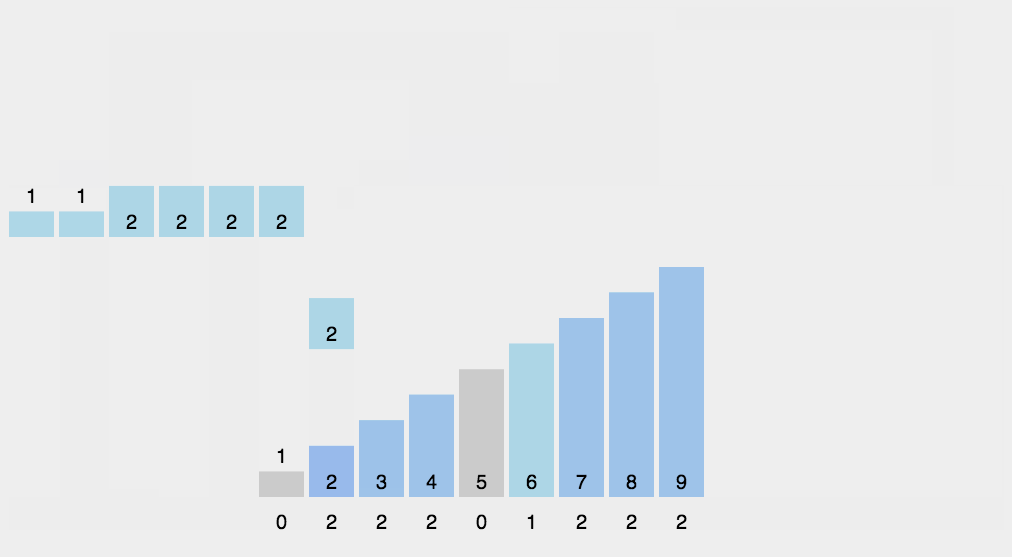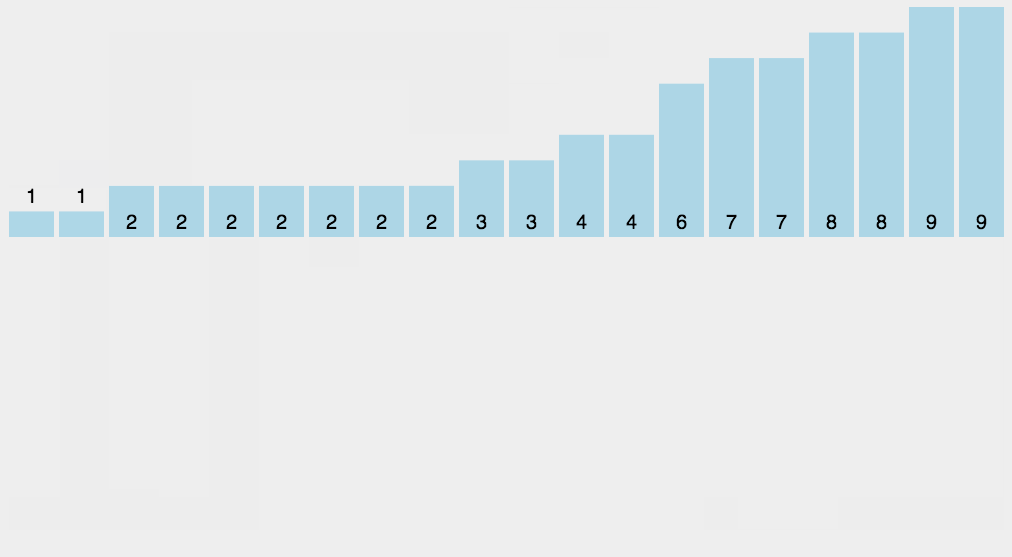
计数排序算法
计数排序 计数排序说明: 计数排序(Counting Sort)是一种非比较性的排序算法,它通过统计元素出现的次数,然后根据元素出现的次数将元素排列在正确的位置上,从而实现排序。计数排序适用于非负整数或者具有确…...

企业高性能web服务器-nginx
1.nginx简介: nginx是企业高可用的web服务器,nginx也可用来做反向代理服务器器,具有高并发,占用资源少,功能丰富,也可以作为简单的负载均衡。 nginx在企业中的功能: web服务软件 反向代理服务器…...
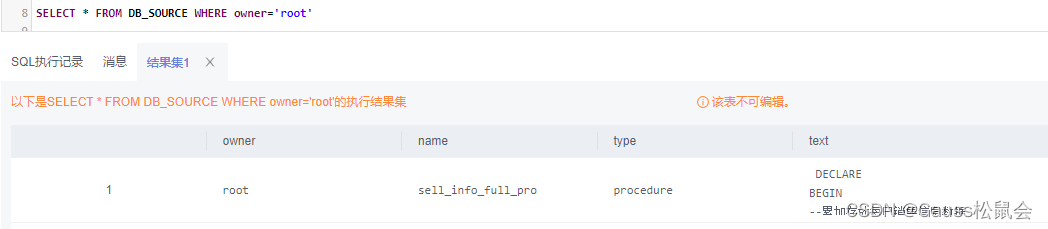
GaussDB数据库的元数据及其管理简介
目录 一、前言 二、元数据简介 1、元数据定义 2、元数据分类 3、数据库元数据管理 三、GaussDB数据库的元数据管理 1、GaussDB数据库的元数据管理 2、通过“SQL 系统表/系统视图/系统函数”的方式管理(采集)元数据 1)获取表、视图及…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...
