【机器学习】西瓜书学习心得及课后习题参考答案—第6章支持向量机
笔记心得
6.1 间隔与支持向量—— w w w是法向量,垂直与超平面 w T x + b = 0 w^Tx+b=0 wTx+b=0。这一节了解了支持向量机的基本型。
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 s . t . y i ( w T x i + b ) ≥ 1 , i = 1 , 2 , . . . , m . \min_{w,b} \frac{1}{2}||w||^2 \\ s.t. \ \ y_i(w^Tx_i+b) \ge 1, \qquad i=1,2,...,m. w,bmin21∣∣w∣∣2s.t. yi(wTxi+b)≥1,i=1,2,...,m.
6.2 对偶问题——SVM的基本型是一个凸二次规划问题,可以用更高效的方法求解。使用拉格朗日乘子法得到其“对偶问题”。了解了KKT条件,SMO算法。
6.3 核函数——了解了能作为核函数的条件,和常用的核函数。
6.4 软间隔与正则化——这一节主要是讨论缓解过拟合问题。
6.5 支持向量回归——支持向量机解决回归问题。所构建的间隔带两侧松弛程度可不同。
术语学习
课后习题
6.1 试证明样本空间中任意点 x x x到超平面 ( w , b ) (w,b) (w,b)的距离为式 (6.2)。
假设点 x 0 = ( x 1 0 , x 2 0 , . . . , x n 0 ) x_0=(x_1^0,x_2^0,...,x_n^0) x0=(x10,x20,...,xn0),其在超平面 w T x + b = 0 w^Tx+b=0 wTx+b=0上的投影点为 x 1 = ( x 1 1 , x 2 1 , . . . , x n 1 ) x_1=(x_1^1,x_2^1,...,x_n^1) x1=(x11,x21,...,xn1),则 w T x 1 + b = 0 w^Tx_1+b=0 wTx1+b=0。
w w w为法向量,因此 x 0 x 1 → \overrightarrow{x_{0}x_{1}} x0x1与法向量 w w w平行。夹角为0或者 π \pi π
∣ w ⋅ x 0 x 1 → ∣ = ∣ ∣ ∣ w ∣ ∣ ⋅ c o s π ⋅ ∣ ∣ x 0 x 1 → ∣ ∣ ∣ = ∣ ∣ w ∣ ∣ ⋅ ∣ ∣ x 0 x 1 → ∣ ∣ = ∣ ∣ w ∣ ∣ ⋅ r |w\cdot \overrightarrow{x_0x_1}| = |||w|| \cdot cos\pi \cdot ||\overrightarrow{x_0x_1} ||| = ||w|| \cdot ||\overrightarrow{x_0x_1}|| = ||w||\cdot r ∣w⋅x0x1∣=∣∣∣w∣∣⋅cosπ⋅∣∣x0x1∣∣∣=∣∣w∣∣⋅∣∣x0x1∣∣=∣∣w∣∣⋅r
同时
∣ w ⋅ x 0 x 1 → ∣ = ∣ w 1 ( x 1 1 − x 1 0 ) + w 2 ( x 2 1 − x 2 0 ) + . . . + w 1 ( x n 1 − x n 0 ) ∣ = ∣ w 1 x 1 1 + w 2 x 2 1 + . . . + w n x n 1 − ( w 1 x 1 0 + w 2 x 2 0 + . . . + w n x n 0 ) ∣ = ∣ w T x 1 − w T x 0 ∣ = ∣ − b − w T x 0 ∣ = ∣ w T x 0 + b ∣ |w \cdot \overrightarrow{x_0x_1}| \\ =|w_1(x_1^1-x_1^0)+w_2(x_2^1-x_2^0)+...+w_1(x_n^1-x_n^0)| \\ =|w_1x_1^1+w_2x_2^1+...+w_nx_n^1-(w_1x_1^0+w_2x_2^0+...+w_nx_n^0)| \\ =|w^Tx_1-w^Tx_0| \\ =|-b-w^Tx_0| \\ =|w^Tx_0+b| ∣w⋅x0x1∣=∣w1(x11−x10)+w2(x21−x20)+...+w1(xn1−xn0)∣=∣w1x11+w2x21+...+wnxn1−(w1x10+w2x20+...+wnxn0)∣=∣wTx1−wTx0∣=∣−b−wTx0∣=∣wTx0+b∣
所以
∣ w T x 0 + b ∣ = ∣ ∣ w ∣ ∣ ⋅ r r = ∣ w T x 0 + b ∣ ∣ ∣ w ∣ ∣ |w^Tx_0+b| = ||w||\cdot r \\ r = \frac{|w^Tx_0+b|}{||w||} ∣wTx0+b∣=∣∣w∣∣⋅rr=∣∣w∣∣∣wTx0+b∣
相关文章:

【机器学习】西瓜书学习心得及课后习题参考答案—第6章支持向量机
笔记心得 6.1 间隔与支持向量—— w w w是法向量,垂直与超平面 w T x b 0 w^Txb0 wTxb0。这一节了解了支持向量机的基本型。 min w , b 1 2 ∣ ∣ w ∣ ∣ 2 s . t . y i ( w T x i b ) ≥ 1 , i 1 , 2 , . . . , m . \min_{w,b} \frac{1}{2}||w||^2 \\ s.…...

无涯教程-Perl - 面向对象
Perl中的面向对象概念很大程度上基于引用以及匿名数组和哈希。让我们开始学习面向对象Perl的基本概念。 定义类 在Perl中定义一个类非常简单。类以最简单的形式对应于Perl软件包。要在Perl中创建一个类,我们首先构建一个包。 Perl软件包在Perl程序中提供了一个单…...
Linux安装VScode
从本篇开始,打算有时间就写写在VScode中编写一些ros相关的案例程序用于学习记录。本篇是如何在Linux安装VScode的第一篇。 一、下载VScode 在Linux中打开浏览器输入:https://code.visualstudio.com/Download,选择与你电脑相匹配的版本下载&…...
网络安全(黑客)工具篇
大家好,我是白菜。这篇文章给大家盘点那些年,我们一起玩过的网络安全工具。 一、反恶意代码软件 1.Malwarebytes 这是一个检测和删除恶意的软件,包括蠕虫,木马,后门,流氓,拨号器,…...

测试工程师刚入职如何快速熟悉需求并输出测试用例?
刚入职第一天,早上办完入职,下午就就分配了测试任务,2个模块13条短信验证,2天内输出测试用例(xmind输出功能点,excel书写业务流)。测试负责人给我们快速讲了一下业务,在这过程中大概…...

2023上半年手机及数码行业分析报告(京东销售数据分析)
2023年上半年,手机市场迎来复苏,同环比来看,销量销额纷纷上涨。 而数码市场中,各个热门品类表现不一。微单相机及智能手表同比去年呈现增长态势,而笔记本电脑市场则出现下滑。 基于此现状,鲸参谋发布了20…...
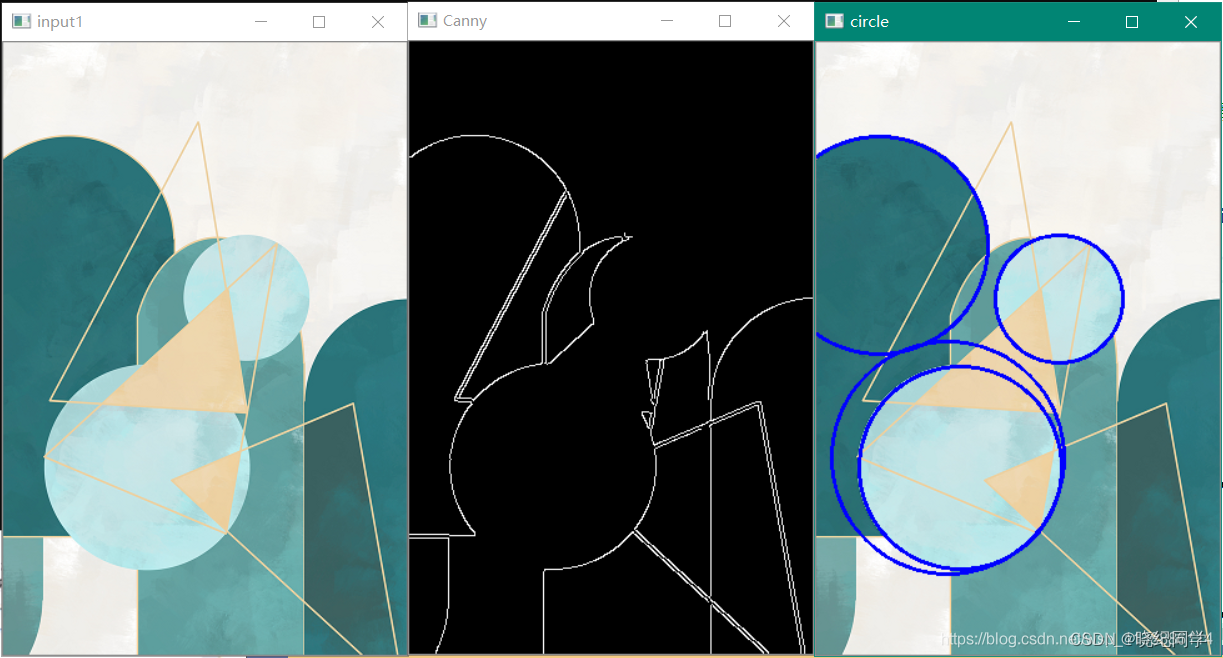
Opencv-C++笔记 (14) : 霍夫变换(直线、圆)
文章目录 一、霍夫变换-直线1.1霍夫变换-直线 原理详解 二、霍夫圆检测 一、霍夫变换-直线 Hough Line Transform用来做直线检测 前提条件 – 边缘检测已经完成 1、平面空间(x,y)到极坐标空间转换; 2、对极坐标进行变换,转化为…...

栈和队列(一) 栈操作详解
文章目录 一、物理结构和逻辑结构二、栈1、什么是栈2、栈中一些基本操作的实现Stack.hStack.c栈的初始化栈的销毁入栈出栈获得栈顶元素获得栈的元素数判断栈空 三、利用栈解决问题 一、物理结构和逻辑结构 栈和队列都属于逻辑结构,它们既可以用数组实现也可以用链表…...

软考A计划-系统集成项目管理工程师-信息系统安全管理-下
点击跳转专栏>Unity3D特效百例点击跳转专栏>案例项目实战源码点击跳转专栏>游戏脚本-辅助自动化点击跳转专栏>Android控件全解手册点击跳转专栏>Scratch编程案例点击跳转>软考全系列点击跳转>蓝桥系列 👉关于作者 专注于Android/Unity和各种游…...

Spark知识点总结
1. Spark支持哪几种运行模式? 本地模式(Local Mode):在这种模式下,Spark在单个机器上运行。所有的Spark操作都在一个单独的JVM进程中进行。这种模式适合开发和测试,但不适合处理大规模的数据。 集群模式&a…...
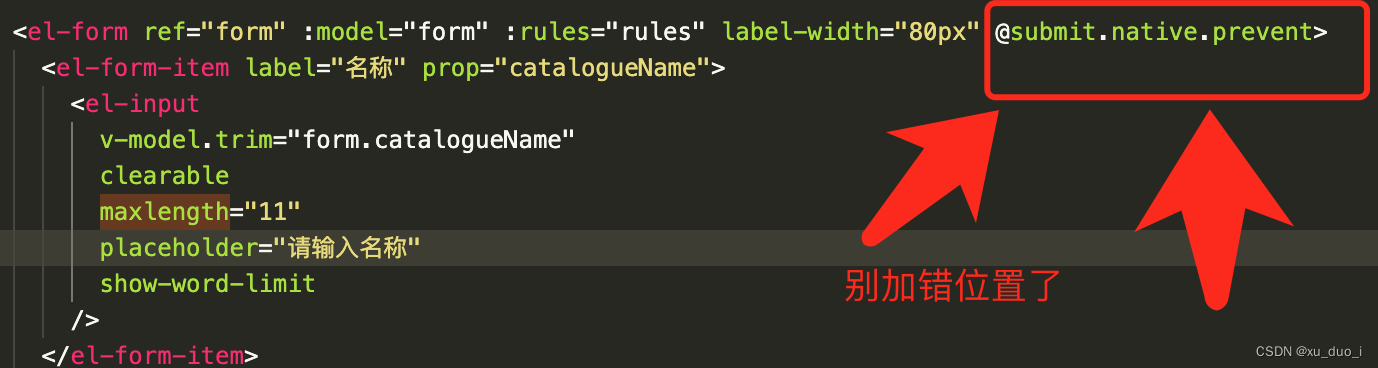
vue el-input 使用 回车键会刷新页面的问题
场景: vue项目中 在输入框输入字符并按下回车键搜索时,不会进行搜索, 而是会刷新页面 原因: 当form表单中只有一个input时,按下回车建会自动触发页面的提交功能, 产生刷新页面的行为 解决: 在…...

【ARM64 常见汇编指令学习 12 -- ARM 汇编函数 的学习】
文章目录 1.1 ARM 汇编函数简介1.1.1 ARM 汇编标签 Label1.1.2 ARM 汇编函数属性指令1.1.3 UEFI 中的函数宏:ASM_FUNC1.1.3.1 UEFI ASM_FUNC 实现汇编函数 1.1.4 UEFI 预编译前缀宏 ASM_PFX 上篇文章:ARM64 常见汇编指令学习 11 – ARM 汇编宏 .macro 的…...

linux下软件安装 - 与GPT对话
1 cmake 没有uninstall 你是对的,CMake 默认情况下并没有提供 make uninstall 目标。这是因为 make install 操作是在特定的目录下进行安装的,CMake 不知道安装到了哪里以及哪些文件被安装了。因此,没有直接支持的 make uninstall 目标来进行卸载。 如果你想要卸载通过 mak…...
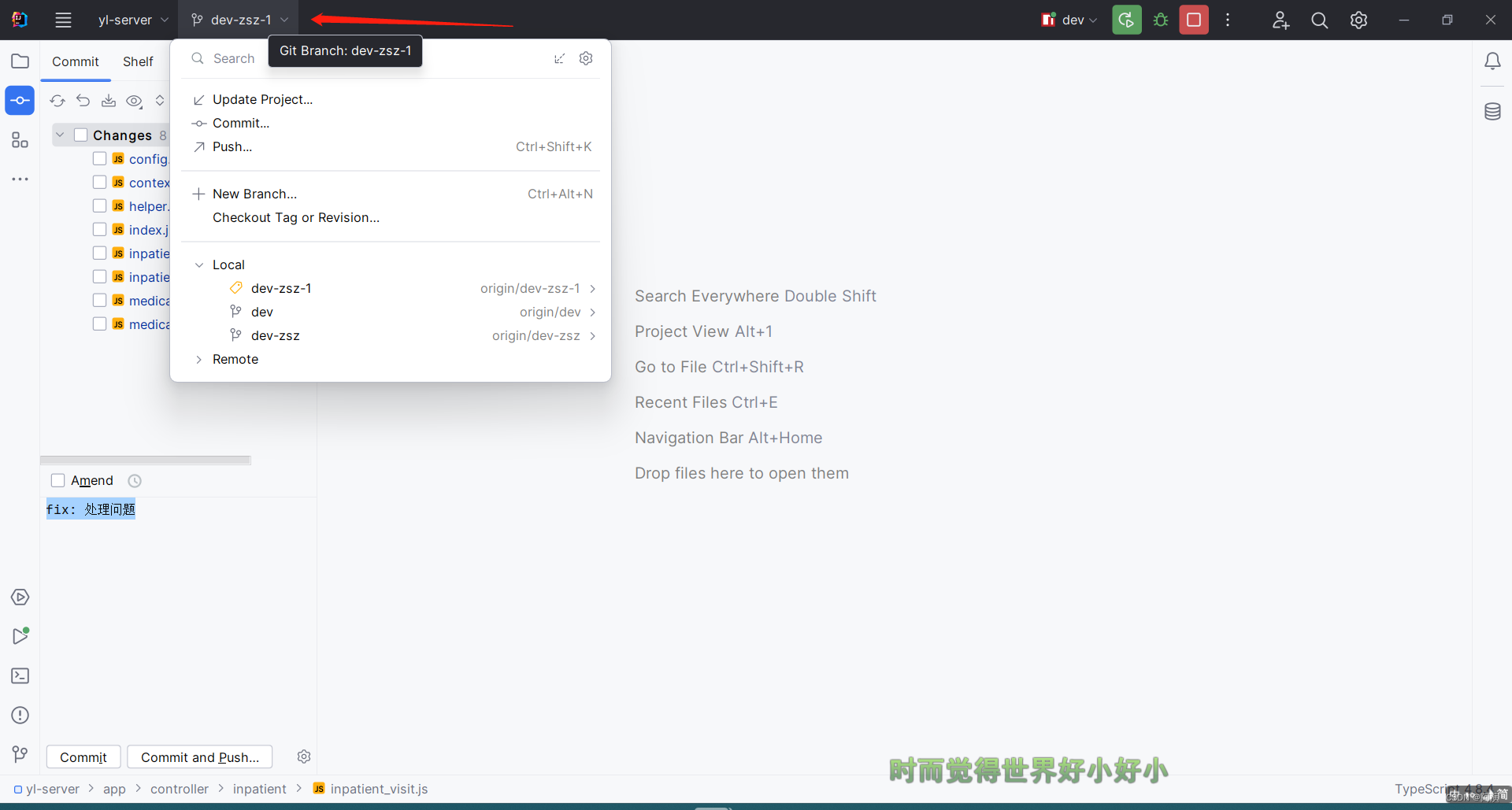
idea 2023 新版ui中git的相关操作
前两个月换了新电脑,下了最新版的idea发现可以切换一套新的ui了 切换新ui肯定不太习惯,很多操作都得重新摸索一下 在这里记录几个git相关的操作 忽略我下面截图中当前项目是js的后端项目…… 切换ui 首先说一下怎么切换新旧版ui,我这里就…...

vue3—SCSS的安装、配置与使用
SCSS 安装 使用npm安装scss: npm install sass sass-loader --save-dev 配置 配置到全局 🌟附赠代码🌟 css: {preprocessorOptions: {scss: {additionalData:import "./src/Function/Easy_I_Function/Echarts/ToSeeEcharts/utill.…...

Godot 4 源码分析 - Path2D与PathFollow2D
学习演示项目dodge_the_creeps,发现里面多了一个Path2D与PathFollow2D 研究GDScript代码发现,它主要用于随机生成Mob var mob_spawn_location get_node(^"MobPath/MobSpawnLocation")mob_spawn_location.progress randi()# Set the mobs dir…...
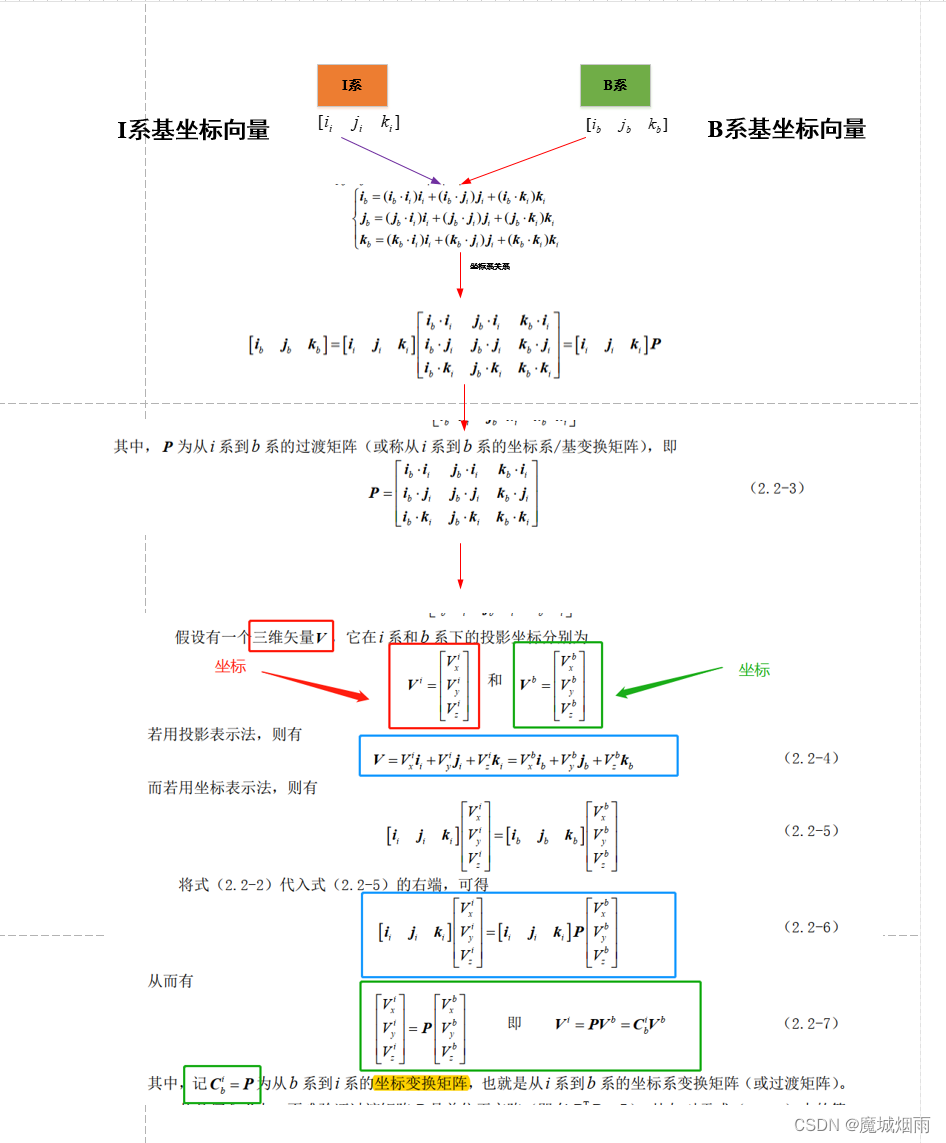
ardupilot 中坐标变换矩阵和坐标系变换矩阵区别
目录 文章目录 目录摘要1.坐标变换矩阵与坐标系变换矩阵摘要 本节主要记录ardupilot 中坐标变换矩阵和坐标系变换矩阵的区别,这里非常重要,特别是进行姿态误差计算时,如果理解错误,很难搞明白后面算法。 1.坐标变换矩阵与坐标系变换矩阵 坐标变换矩阵的本质含义:是可以把…...

VR内容研发公司 | VR流感病毒实验虚拟现实课件
由广州华锐互动开发的《VR流感病毒实验虚拟现实课件》是一种新型的教学模式,可以为学生提供更加真实和直观的流感病毒分离鉴定实验操作体验,从而提高学生的实验技能和工作效率。 《VR流感病毒实验虚拟现实课件》涉及了生物安全二级实验室(BSL-2)和流感病…...

python——案例10:认识if、elif、else
案例10:认识if、elif、elsenumfloat(input("输入数值:")) #用户输入数字if num>0:print("正数")elif num0:print("零") else:print("负数")#输出结果如下:输入数值:-1 负数 输入数值…...

Hadoop中命令检查hdfs的文件是否存在
Hadoop中命令检查hdfs的文件是否存在 在Hadoop中,可以使用以下命令检查HDFS文件是否存在: hadoop fs -test -e 其中,是要检查的HDFS文件的路径。 如果文件存在,命令返回0;如果文件不存在,命令返回非0值…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

轻量级Docker管理工具Docker Switchboard
简介 什么是 Docker Switchboard ? Docker Switchboard 是一个轻量级的 Web 应用程序,用于管理 Docker 容器。它提供了一个干净、用户友好的界面来启动、停止和监控主机上运行的容器,使其成为本地开发、家庭实验室或小型服务器设置的理想选择…...
