C++二叉搜索树剖析

目录
- 🍇二叉搜索树概念
- 🍈二叉搜索树查找
- 🍉二叉搜索树的插入
- 🍊二叉搜索树的删除
- 🍍二叉搜索树的查找、插入、删除实现
- 🍋二叉搜索树的应用
- 🥭二叉搜索树的性能分析
- 🍓总结
🍇二叉搜索树概念
二叉搜索树,又称为二叉排序树,是一种特殊的二叉树。它要么是一棵空树,要么具有以下性质:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值;
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值;
- 它的左右子树也分别为二叉搜索树。
二叉搜索树的特点是可以快速地查找、插入和删除节点,因为它的节点按照大小关系排列,形成了一种有序结构。它常被用于实现关联数组、集合等数据结构,也是许多其他算法的基础。

🍈二叉搜索树查找
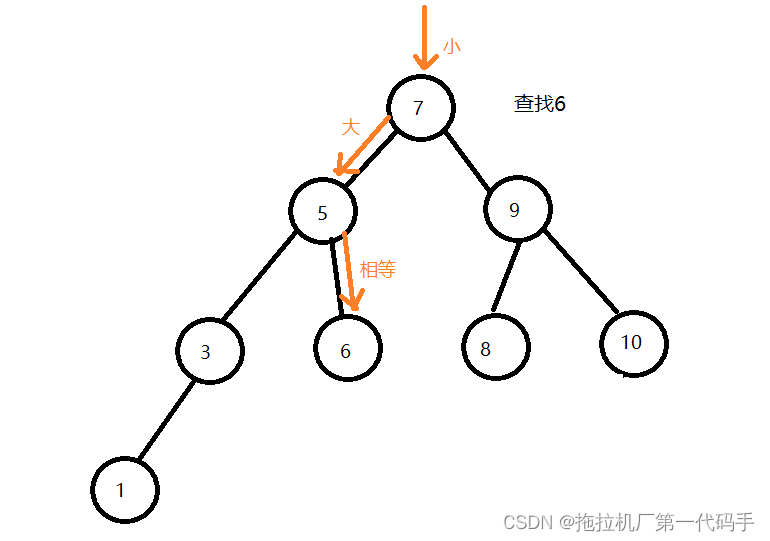
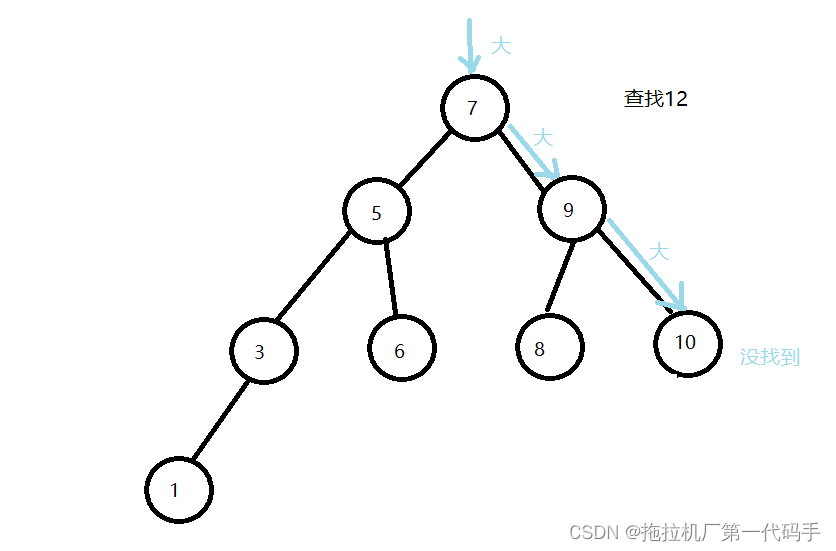
二叉搜索树的查找可以通过以下步骤进行:
-
从根节点开始比较,将待查找的值与根节点的值进行比较,如果相等,则返回该节点;如果待查找的值比根节点的值大,则往右子树走查找,反之则往左子树走查找。
-
重复上述步骤,直到找到待查找的值或者走到空节点仍未找到。如果走到空节点仍未找到,则说明该值不存在于二叉搜索树中。
由于二叉搜索树的节点按照大小关系排列,因此查找的时间复杂度为O(log n),其中n为二叉搜索树中节点的个数。
🍉二叉搜索树的插入
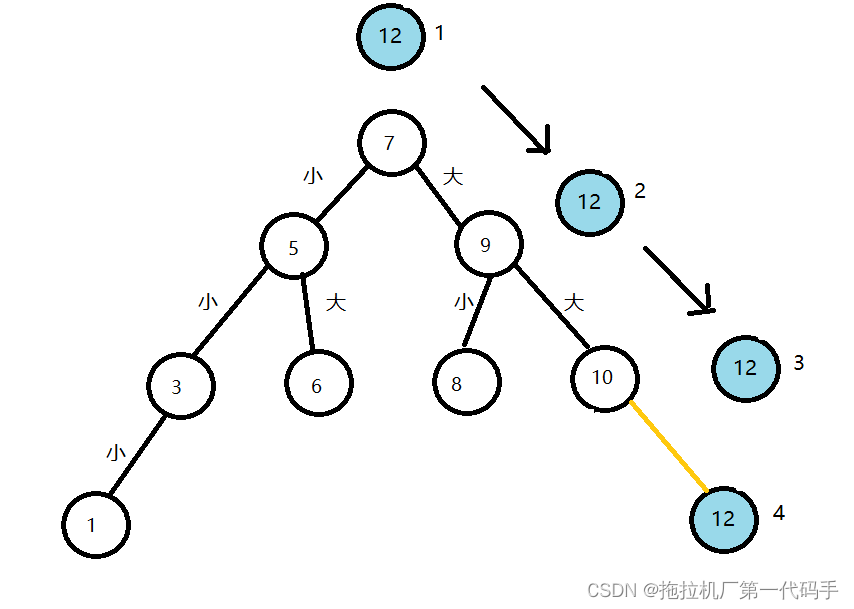
二叉搜索树的插入可以通过以下步骤进行:
-
如果二叉搜索树为空,则直接将新节点作为根节点,赋值给root指针。
-
如果二叉搜索树不为空,则按照二叉搜索树的性质,从根节点开始比较待插入节点的值和当前节点的值的大小关系,如果待插入节点的值比当前节点的值小,则往左子树走查找,如果左子树为空,则将待插入节点作为当前节点的左子节点;
-
如果待插入节点的值比当前节点的值大,则往右子树走查找,如果右子树为空,则将待插入节点作为当前节点的右子节点。
-
如果待插入节点的值与当前节点值相等,表示已经存在这个值,插入失败。
-
重复上述步骤,直到找到合适的插入位置为止。
二叉搜索树的插入时间复杂度为O(log n),其中n为二叉搜索树中节点的个数。
🍊二叉搜索树的删除
二叉搜索树的删除可以通过以下步骤进行:
首先查找待删除的节点是否在二叉搜索树中,如果不存在,则直接返回;否则,进入下一步操作。
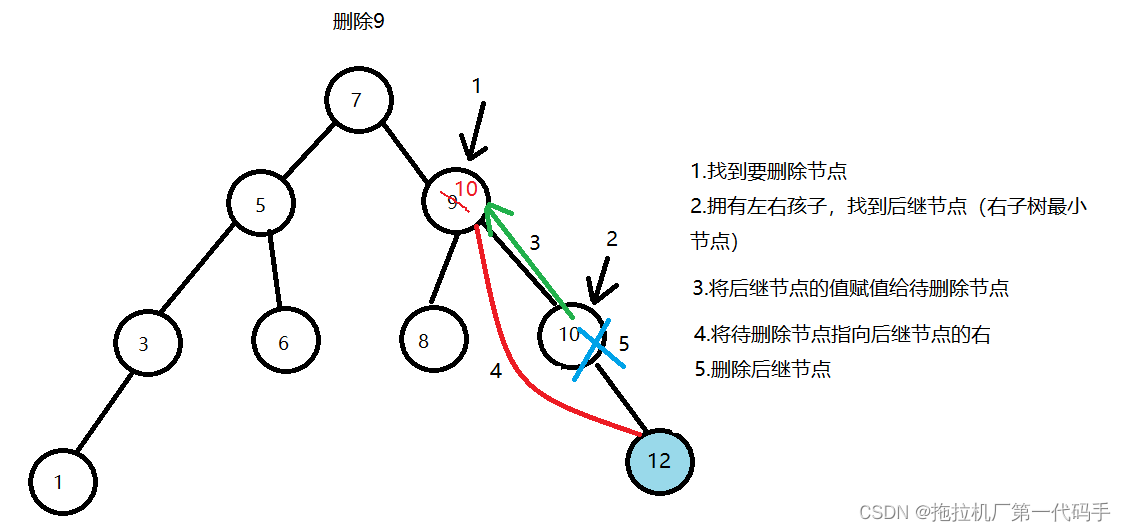
根据待删除节点的情况,进行以下处理:
-
如果待删除节点是叶子节点,则直接删除该节点即可。
-
如果待删除节点只有左子树或者右子树,则将待删除节点的父节点指向待删除节点的子节点,然后删除待删除节点。
-
如果待删除节点既有左子树又有右子树,则需要找到它的中序遍历下的后继节点(即右子树中的最小节点),将后继节点的值赋给待删除节点,然后将待删除节点的右指向后继节点的右,然后删除后继节点。
重复上述步骤,直到完成待删除节点的删除。
需要注意的是,二叉搜索树的删除操作可能会影响树的结构,因此需要对树进行平衡操作,以保证二叉搜索树的性质不被破坏。
二叉搜索树的删除时间复杂度为O(log n),其中n为二叉搜索树中节点的个数。
🍍二叉搜索树的查找、插入、删除实现
- 二叉搜索树节点的定义
template<class k>
class BStreeNode
{
public:BStreeNode(const k& key):_key(key), _left(nullptr), _right(nullptr){}k _key;BStreeNode* _left;BStreeNode* _right;
};
二叉搜索树节点的定义有以下成员:
-
key:表示节点的关键码,用于比较节点的大小关系,通常是一个模板类型,可以是整型、字符型、字符串、自定义类型等。
-
left:表示节点的左子节点,通常是一个指向BStreeNode类型的指针,如果节点没有左子节点,则该指针为空指针nullptr。
-
right:表示节点的右子节点,通常是一个指向BStreeNode类型的指针,如果节点没有右子节点,则该指针为空指针nullptr。
- 二叉搜索树的定义
template<class k>
class BStree
{typedef BStreeNode<k> Node;
public:Node* find(const k& key);bool insert(const k& key);bool erase(const k& key); void InOrder();
private:Node* _root = nullptr;void _InOrder(const Node* root);
};
二叉搜索树的定义包括以下成员:
-
Node:表示二叉树的节点,通常是一个模板类,包括节点的关键码、左子节点、右子节点等成员。
-
find():用于在二叉树中查找指定关键码的节点,如果找到,则返回该节点的指针;否则返回空指针nullptr。
-
insert():用于向二叉树中插入一个新节点,如果插入成功,则返回true;否则返回false。
-
erase():用于从二叉树中删除指定关键码的节点,如果删除成功,则返回true;否则返回false。
-
InOrder():用于对二叉树进行中序遍历,按照节点的关键码从小到大输出节点的值。
- 二叉搜索树查找实现
Node* find(const k& key){Node* cur = _root;while (cur){if (cur->_key < key) cur = cur->_right; else if (cur->_key > key)cur = cur->_left;elsereturn cur;}return nullptr;}
二叉搜索树的查找操作可以通过比较节点的键值来实现。从根节点开始,若当前节点的键值小于要查找的键值,则继续在右子树中查找;若当前节点的键值大于要查找的键值,则继续在左子树中查找;若当前节点的键值等于要查找的键值,则返回当前节点。
上述代码实现了二叉搜索树的查找操作。从根节点开始,通过循环遍历整棵树,比较节点的键值,根据大小关系移动到左子树或右子树中,直到找到要查找的节点或遍历到叶子节点为止。如果找到了要查找的节点,则返回该节点指针;否则返回空指针。
- 二叉搜索树插入实现
bool insert(const k& key){//空树if (_root == nullptr){Node* newnode = new Node(key);_root = newnode;return true;}//不为空Node* cur = _root;Node* parent = nullptr;while (cur){parent = cur;if (cur->_key < key)cur = cur->_right;else if (cur->_key > key)cur = cur->_left;elsereturn false;}Node* newnode = new Node(key);parent->_key > key ? parent->_left = newnode : parent->_right = newnode;return true;}
二叉搜索树的插入操作可以通过比较节点的键值来实现。从根节点开始,若要插入的键值小于当前节点的键值,则继续在左子树中插入;若要插入的键值大于当前节点的键值,则继续在右子树中插入;若要插入的键值等于当前节点的键值,则返回插入失败。
上述代码实现了二叉搜索树的插入操作。首先判断树是否为空,如果为空,则直接将新节点作为根节点;否则,从根节点开始循环遍历整棵树,比较节点的键值,根据大小关系移动到左子树或右子树中,直到找到合适的插入位置或遍历到叶子节点为止。如果找到了合适的插入位置,则创建新节点并插入到该位置;否则返回插入失败。
- 二叉搜索树删除的实现
bool erase(const k& key){//查找该节点及其父亲节点Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;} elsebreak;}if (cur == nullptr)return false;//为叶子节点else if (cur->_left == nullptr && cur->_right == nullptr)delete cur;//只有一个孩子else if ((cur->_left == nullptr && cur->_right) || (cur->_left && cur->_right == nullptr)){if (parent->_left == cur){cur->_left == nullptr ? parent->_left = cur->_right : parent->_left = cur->_left;}else{cur->_left == nullptr ? parent->_right = cur->_right : parent->_right = cur->_left;}delete cur;}//有两个孩子else if (cur->_left && cur->_right){Node* del = cur->_right;//找右子树最小节点while (del->_left){del = del->_left;}//赋值cur->_key = del->_key;//待删除节点的右指向最小节点右cur->_right = del->_right;//删除最小节点delete del;}return true;}
二叉搜索树的删除操作比较复杂,需要考虑删除节点的情况分为三种:
-
待删除节点为叶子节点:直接删除该节点即可。
-
待删除节点只有一个孩子:将该节点的孩子节点接到该节点的父节点上,然后删除该节点。
-
待删除节点有两个孩子:找到该节点的右子树中的最小节点,将其键值赋值给待删除节点,然后删除最小节点。
上述代码实现了二叉搜索树的删除操作。首先从根节点开始循环遍历整棵树,查找待删除节点及其父节点。如果没有找到待删除节点,则返回删除失败;否则根据待删除节点的情况进行不同的操作。如果待删除节点为叶子节点,则直接删除该节点;如果待删除节点只有一个孩子,则将孩子节点接到父节点上,然后删除该节点;如果待删除节点有两个孩子,则找到右子树中的最小节点,将其键值赋值给待删除节点,然后删除最小节点。最后返回删除成功。
- 二叉搜索树中序遍历实现
void _InOrder(const Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << ' ';_InOrder(root->_right);}
二叉搜索树的中序遍历是指按照节点键值的大小关系,先遍历左子树,再遍历根节点,最后遍历右子树。因为二叉搜索树的中序遍历结果是一个有序序列,因此可以使用中序遍历来实现对二叉搜索树的排序操作。
上述代码实现了二叉搜索树的中序遍历操作。首先判断当前节点是否为空,如果为空则返回;否则按照左子树、根节点、右子树的顺序递归遍历整棵树,并输出节点的键值。
🍋二叉搜索树的应用
-
K模型:K模型是指只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索的值。例如,可以以词库中所有单词集合中的每个单词作为key,构建一棵二叉搜索树,在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。
-
KV模型:KV模型是指每一个关键码key都有与之对应的值Value,即<Key, Value>的键值对。该种方式在现实生活中非常常见,例如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文<word, chinese>就构成一种键值对;再比如统计单词次数,统计成功后,给定单词就可以快速找到其出现的次数,单词与其出现次数就是<word, count>就构成一种键值对。二叉搜索树可以用来实现KV模型,以key作为二叉搜索树的节点,value作为节点的值,通过比较key的大小关系来实现快速查找、插入和删除节点的操作。
将上述二叉搜索树修改为KV模型:
- 二叉树节点定义示例代码
template<class K, class V>
class BStreeNode
{
public:BStreeNode(const K& key, const V& value):_key(key), _value(value), _left(nullptr), _right(nullptr){}K _key;V _value;BStreeNode* _left;BStreeNode* _right;
};
- 中序输出代码:
void _InOrder(const Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << ":" << root->_value << endl;_InOrder(root->_right);}
- 测试代码:
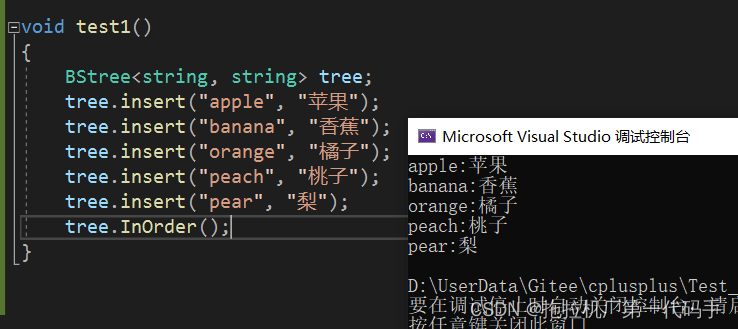
void test1()
{BStree<string, string> tree;tree.insert("apple", "苹果");tree.insert("banana", "香蕉");tree.insert("orange", "橘子");tree.insert("peach", "桃子");tree.insert("pear", "梨");tree.InOrder();
}
运行结果:
🥭二叉搜索树的性能分析
插入和删除操作都需要先进行查找操作,因此二叉搜索树的查找效率代表了二叉搜索树各个操作的性能。对于有n个节点的二叉搜索树,如果每个元素查找的概率相等,那么二叉搜索树的平均查找长度是节点在二叉搜索树的深度的函数,即节点越深,则比较次数越多。
需要注意的是,对于同一个关键码集合,如果各关键码插入的次序不同,可能会得到不同结构的二叉搜索树。因为二叉搜索树的结构取决于插入顺序,如果插入的顺序不同,可能会导致树的结构不同,进而影响树的查找效率。因此,在实际应用中,需要根据实际情况选择合适的插入顺序,以获得更好的性能。
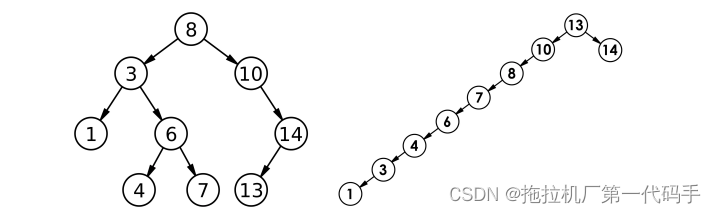
最优情况下,二叉搜索树的高度为 log2N,每一次查找可以将搜索范围缩小一半,因此平均比较次数为 log2N。
最差情况下,二叉搜索树的高度为 (N-1),每一次查找只能将搜索范围缩小一层,因此平均比较次数为 (1+2+…+N)/N = (N+1)/2,约等于 N/2。这种情况发生在插入的数据是有序的时候,导致二叉搜索树退化为链表。此时可以使用平衡二叉树来解决这个问题。
🍓总结
二叉搜索树是一种非常常见的数据结构,它是一棵二叉树,其中每个节点都包含一个键值,且左子树的所有节点的键值小于当前节点的键值,右子树的所有节点的键值大于当前节点的键值。这种特定的结构使得二叉搜索树能够快速地进行查找、插入、删除等操作。
在实际应用中,二叉搜索树被广泛使用,如在数据库索引、编译器符号表、路由表等领域。对于一个包含n个节点的二叉搜索树,其查找、插入、删除的时间复杂度均为O(logn),这使得它在处理大数据量时具有很高的效率。
但是,二叉搜索树也存在一些问题。当数据集合中的元素是随机分布的时,二叉搜索树的性能是非常好的。但是,当数据集合中的元素是有序的时,二叉搜索树的性能会退化为O(n),这就是所谓的“不平衡问题”。为了解决这个问题,我们可以使用平衡二叉树、红黑树等数据结构来优化二叉搜索树。
此外,二叉搜索树在插入重复元素时也存在问题。如果我们简单地将重复元素插入到二叉搜索树中,那么查找和删除操作就会变得非常麻烦。为了解决这个问题,我们可以使用多重集合、哈希表等数据结构来处理重复元素。
总之,二叉搜索树是一种非常重要的数据结构,它能够快速地进行查找、插入、删除等操作,但是在实际应用中需要注意避免和解决一些问题,如不平衡问题、重复元素问题等。
文章总结不易,如果觉得有所帮助的话就👍,文中所有代码均放在gitee上,关注博主,持续更新中…

相关文章:

C++二叉搜索树剖析
目录 🍇二叉搜索树概念🍈二叉搜索树查找🍉二叉搜索树的插入🍊二叉搜索树的删除🍍二叉搜索树的查找、插入、删除实现🍋二叉搜索树的应用🥭二叉搜索树的性能分析🍓总结 🍇二…...
升级你的GitHub终端认证方式:从密码到令牌
升级你的GitHub终端认证方式:从密码到令牌 前言 GitHub官方在2021年8月14日进行了一次重大改变,它将终端推送代码时所需的身份认证方式从密码验证升级为使用个人访问令牌(Personal Access Token)。这个改变引起了一些新的挑战&am…...
【力扣】链表题目总结
文章目录 链表基础题型一、单链表翻转、反转、旋转1.反转链表2.反转链表II——反转部分链表3.旋转链表4.K个一组翻转链表5.反转偶数长度组的节点 二、删除单链表中的结点1.删除链表的结点2.删除未排序链表中的重复节点3.删除已排序链表中的重复元素I——重复元素只剩下一个4.删…...

Thunar配置自定义动作
Add “Copy To” and “Move To” custom actions in Thunar file manager | For the record 1.在此打开终端 图标-应用程序:utilities-terminal 命令:exo-open --working-directory %f --launch TerminalEmulator 文件类型:* 目录 2.右键增…...
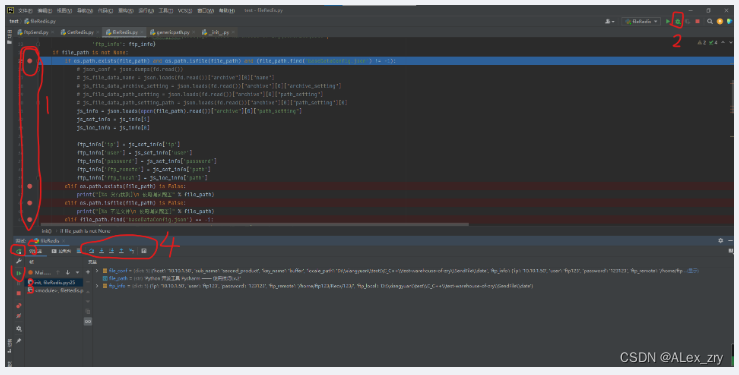
Python 开发工具 Pycharm —— 使用技巧Lv.3
单步执行调试 1: 鼠标左键单击红点是断点行 2:甲虫样式是进行调试方式运行,鼠标左键单击点击 3: 单步运行图标,点击让程序运行一行 4: 步入步出,可以进入当前代码行函数内 5:重新运行…...
51单片机(普中HC6800-EM3 V3.0)实验例程软件分析 实验三 LED流水灯
目录 前言 一、原理图及知识点介绍 二、代码分析 知识点五:#include 中的库函数解析 _crol_,_irol_,_lrol_ _cror_,_iror_,_lror_ _nop_ _testbit_ 前言 第一个实验:51单片机(普中HC6800-EM3 V3.0…...

深度学习与计算机相结合:直播实时美颜SDK的创新之路
时下,实时美颜技术就成为了直播主们的得力工具,它可以在直播过程中即时处理视频画面。而支持实时美颜功能的SDK更是推动了这项技术的发展,让直播主和普通用户都能轻松使用美颜功能。 一、美颜技术的演进 早期的美颜技术主要依赖于简单的图…...

Unity寻找子物体的方法
1.GetComponentsInChildren() 查找单个子物体 GameObject childObjectGetComponentInChildren<Transform>(); 查找多个子物体 Transform[] myTransforms GetComponentsInChildren<Transform>(); foreach (var child in myTransforms){ Debug.Log(child.name…...

车载软件架构 —— 车载软件安全启动关键技术解读
车载软件架构 —— 车载软件安全启动关键技术解读 我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 没有人关注你。也无需有人关注你。你必须承认自己的价值,你不能站在他人的角度来反对自己。人生…...

2023-08-05——JVM Method Area(方法区)
方法区 Method Area(方法区) 方法区是指被所有线程共享的,字段和方法字节码,以及一些特殊方法,如构造函数,接口代码在此定义,简单的说就是所有的定义方法信息都保存在此区域,此区域…...
【前端知识】React 基础巩固(四十六)——自定义Hook的应用
React 基础巩固(四十六)——自定义Hook的应用 一、自定义Hook的应用 自定义Hook本质上只是一种函数代码逻辑的抽取,严格意义上而言,它并不算React的特性。 实现组件创建/销毁时打印日志 import React, { memo, useEffect, useState } from "react…...
Swish - Mac 触控板手势窗口管理工具[macOS]
Swish for Mac是一款Mac触控板增强工具,借助直观的两指轻扫,捏合,轻击和按住手势,就可以从触控板上控制窗口和应用程序。 Swish for Mac又不仅仅只是一个窗口管理器,Swish具有28个易于使用的标题栏,停靠栏…...

【雕爷学编程】MicroPython动手做(31)——物联网之Easy IoT 2
1、物联网的诞生 美国计算机巨头微软(Microsoft)创办人、世界首富比尔盖茨,在1995年出版的《未来之路》一书中,提及“物物互联”。1998年麻省理工学院提出,当时被称作EPC系统的物联网构想。2005年11月,国际电信联盟发布《ITU互联网…...
C# 简单模拟 程序内部 消息订阅发布功能
文章目录 前言模拟消息订阅发布使用注意事项 前言 我想做个简单的消息发布订阅功能,但是发现好像没有现成的工具类。要么就是Mqtt这种消息订阅发布。但是我只想程序内部进行消息订阅发布,进行程序的解耦。那没办法了,只能自己上了 模拟消息…...

第六章 支持向量机
文章目录 支持向量机间隔和支持向量对偶问题问题推导SMO 核函数实验 支持向量机 ⽀持向量机(Support Vector Machines,SVM) 优点:泛化错误率低,计算开销不⼤,结果易解释。缺点:对参数调节和核…...

Docker基本操作之删除容器Container和删除镜像IMAGE
一、删除容器Container语法 docker rm [OPTIONS] CONTAINER [CONTAINER...]OPTIONS参数说明: -f :通过 SIGKILL 信号强制删除一个运行中的容器。【注意是正在运行的容器实例】-l :移除容器间的网络连接,而非容器本身。-v :删除与容器关联的卷。即删除容…...
vue 3.0 + element-ui MessageBox弹出框的 让文本框显示文字 placeholder
inputPlaceholder:请填写理由, 方法实现如下: this.$prompt(, 是否确认?, { confirmButtonText: 确定, cancelButtonText: 取消, inputPlaceholder:请填写理由, }).then(({ value }) > { if(value null || value ""){ Message({message: 请填…...
QT生成可执行文件的步骤
QT生成可执行文件的步骤 第一步:debug为release,然后进行编译 第二步:添加QT生成必要的库 首先,建立一个新的文件夹,然后将Release中的可执行文件拷贝到新的文件夹中 然后,在新建文件夹中生成必要的库 …...
一分钟学会JS获取当前年近五年的年份
先看效果图 上代码: 1、HTML <div><el-date-pickerv-model"queryYearXmgk.startYear"format"yyyy"value-format"yyyy"type"year"placeholder"开始"clearable:picker-options"pickerStartAuditYe…...

14 springboot项目——首页跳转实现
templates里的静态资源无法访问,需要写mvc的配置类或者改application.xml配置文件实现首页访问。这两个方式用其中一种即可,否则会冲突。 14.1 首页跳转方式一 创建配置类,在config包中创建一个mvc的配置类: package jiang.com.s…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...
