PSO粒子群优化算法
PSO粒子群优化算法
- 算法思想
- matlab代码
- python代码
算法思想
粒子群算法(Particle Swarm Optimization)



优点:
1)原理比较简单,实现容易,参数少。
缺点:
1)易早熟收敛至局部最优、迭代后期收敛速度慢的。
算法拓展
针对标准PSO的缺点,通常有如下的改进:
- 实现参数的自适应变化。
- 引入一些其他机制。比如随机的因素,速度、位置的边界变化-后期压缩最大速度等。
- 结合其他智能优化算法:遗传算法、免疫算法、模拟退火算法等等,帮助粒子跳出局部最优,改善收敛速度。
matlab代码
二维下
%% 初始化种群
clear
%% Sphere
clear
f= @(x) x .* sin(x) .* cos(2 * x) - 2 * x .* sin(3 * x) +3 * x .* sin(4 * x); % 函数表达式 % 求这个函数的最大值 N = 20; % 初始种群个数
d = 1; % 可行解维数
ger = 100; % 最大迭代次数
limit = [0, 50]; % 设置位置参数限制
vlimit = [-10, 10]; % 设置速度限制
w = 0.8; % 惯性权重
c1 = 0.5; % 自我学习因子
c2 = 0.5; % 群体学习因子
figure(1);ezplot(f,[0,0.01,limit(2)]); %曲线x = limit(1) + ( limit( 2 ) - limit( 1) ) .* rand(N, d);%初始种群的位置v = rand(N, d); % 初始种群的速度
xm = x; % 每个个体的历史最佳位置
ym = zeros(1, d); % 种群的历史最佳位置
fxm = ones(N, 1)*inf; % 每个个体的历史最佳适应度
fym = inf; % 种群历史最佳适应度
hold on
plot(xm, f(xm), 'ro');title('初始状态图');
figure(2)
%% 群体更新
iter = 1;
% record = zeros(ger, 1); % 记录器
while iter <= ger fx = f(x) ; % 个体当前适应度 for i = 1:N if fx(i) <fxm(i) fxm(i) = fx(i); % 更新个体历史最佳适应度 xm(i,:) = x(i,:); % 更新个体历史最佳位置(取值第i行的所有列) end end if min(fxm) < fym [fym, nmin] = min(fxm); % 更新群体历史最佳适应度 ym = xm(nmin, :); % 更新群体历史最佳位置 end v = v * w + c1 * rand * (xm - x) + c2 * rand * (repmat(ym, N, 1) - x);% 速度更新 % 边界速度处理 v(v > vlimit(2)) = vlimit(2); %可以根据括号中的条件决定是否赋值v(v < vlimit(1)) = vlimit(1); x = x + v;% 位置更新 % 边界位置处理 x(x > limit(2)) = limit(2); x(x < limit(1)) = limit(1); record(iter) = fym;%最大值记录 x0 = 0 : 0.01 : limit(2); %1行3列的数组subplot(1,2,1)plot(x0, f(x0), 'b-', x, f(x), 'ro');title('状态位置变化')subplot(1,2,2);plot(record);title('最优适应度进化过程') pause(0.01) iter = iter+1; end x0 = 0 : 0.01 : limit(2);
figure(4);plot(x0, f(x0), 'b-', x, f(x), 'ro');title('最终状态位置')
disp(['最大值:',num2str(fym)]);
disp(['变量取值:',num2str(ym)]);


三维下
%% 初始化种群
clear
clc
f = @(x,y) 20 + x.^2 + y.^2 - 10*cos(2*pi.*x) - 10*cos(2*pi.*y) ;%[-5.12 ,5.12 ]x0 = [-5.12:0.05:5.12];
y0 = x0 ;
[X,Y] = meshgrid(x0,y0);
Z =f(X,Y) ;
figure(1); mesh(X,Y,Z);
colormap(parula(5));N = 50; % 初始种群个数
d = 2; % 可行解维数
ger = 100; % 最大迭代次数
limit = [-5.12,5.12]; % 设置位置参数限制
vlimit = [-.5, .5]; % 设置速度限制
w = 0.8; % 惯性权重
c1 = 0.5; % 自我学习因子
c2 = 0.5; % 群体学习因子 x = limit(1) + ( limit( 2 ) - limit( 1) ) .* rand(N, d);%初始种群的位置 v = rand(N, d); % 初始种群的速度
xm = x; % 每个个体的历史最佳位置
ym = zeros(1, d); % 种群的历史最佳位置
fxm = ones(N, 1)*inf; % 每个个体的历史最佳适应度
fym = inf; % 种群历史最佳适应度
% record = zeros(ger,1);
hold on
% [X,Y] = meshgrid(x(:,1),x(:,2));
% Z = f( X,Y ) ;
scatter3( x(:,1),x(:,2) ,f( x(:,1),x(:,2) ),'r*' );
figure(2)
record=[];%% 群体更新
iter = 1;
% record = zeros(ger, 1); % 记录器
while iter <= ger fx = f( x(:,1),x(:,2) ) ;% 个体当前适应度 for i = 1:N if fx(i) <fxm(i) fxm(i) = fx(i); % 更新个体历史最佳适应度 xm(i,:) = x(i,:); % 更新个体历史最佳位置(取值) end end if min(fxm)< fym[fym, nmin] = min(fxm); % 更新群体历史最佳适应度 ym = xm(nmin, :); % 更新群体历史最佳位置 end v = v * w + c1 * rand * (xm - x) + c2 * rand * (repmat(ym, N, 1) - x);% 速度更新 % 边界速度处理 v(v > vlimit(2)) = vlimit(2); v(v < vlimit(1)) = vlimit(1); x = x + v;% 位置更新 % 边界位置处理 x(x > limit(2)) = limit(2); x(x < limit(1)) = limit(1); record(iter) = fym;%最大值记录 subplot(1,2,1)mesh(X,Y,Z)hold on scatter3( x(:,1),x(:,2) ,f( x(:,1),x(:,2) ) ,'r*');title(['状态位置变化','-迭代次数:',num2str(iter)])subplot(1,2,2);plot(record);title('最优适应度进化过程') pause(0.01) iter = iter+1; end figure(4);mesh(X,Y,Z); hold on
scatter3( x(:,1),x(:,2) ,f( x(:,1),x(:,2) ) ,'r*');title('最终状态位置')
disp(['最优值:',num2str(fym)]);
disp(['变量取值:',num2str(ym)]); 


python代码
import numpy as np
import matplotlib.pyplot as plt
# 粒子(鸟)
class particle:def __init__(self):self.pos = 0 # 粒子当前位置self.speed = 0self.pbest = 0 # 粒子历史最好位置class PSO:def __init__(self):self.w = 0.5 # 惯性因子self.c1 = 1 # 自我认知学习因子self.c2 = 1 # 社会认知学习因子self.gbest = 0 # 种群当前最好位置self.N = 20 # 种群中粒子数量self.POP = [] # 种群self.iter_N = 100 # 迭代次数# 适应度值计算函数def fitness(self, x):return x + 16 * np.sin(5 * x) + 10 * np.cos(4 * x)# 找到全局最优解def g_best(self, pop):for bird in pop:if bird.fitness > self.fitness(self.gbest):self.gbest = bird.pos# 初始化种群def initPopulation(self, pop, N):for i in range(N):bird = particle()#初始化鸟bird.pos = np.random.uniform(-10, 10)#均匀分布bird.fitness = self.fitness(bird.pos)bird.pbest = bird.fitnesspop.append(bird)# 找到种群中的最优位置self.g_best(pop)# 更新速度和位置def update(self, pop):for bird in pop:# 速度更新speed = self.w * bird.speed + self.c1 * np.random.random() * (bird.pbest - bird.pos) + self.c2 * np.random.random() * (self.gbest - bird.pos)# 位置更新pos = bird.pos + speedif -10 < pos < 10: # 必须在搜索空间内bird.pos = posbird.speed = speed# 更新适应度bird.fitness = self.fitness(bird.pos)# 是否需要更新本粒子历史最好位置if bird.fitness > self.fitness(bird.pbest):bird.pbest = bird.pos# 最终执行def implement(self):# 初始化种群self.initPopulation(self.POP, self.N)# 迭代for i in range(self.iter_N):# 更新速度和位置self.update(self.POP)# 更新种群中最好位置self.g_best(self.POP)pso = PSO()
pso.implement()best_x=0
best_y=0
for ind in pso.POP:#print("x=", ind.pos, "f(x)=", ind.fitness)if ind.fitness>best_y:best_y=ind.fitnessbest_x=ind.pos
print(best_y)
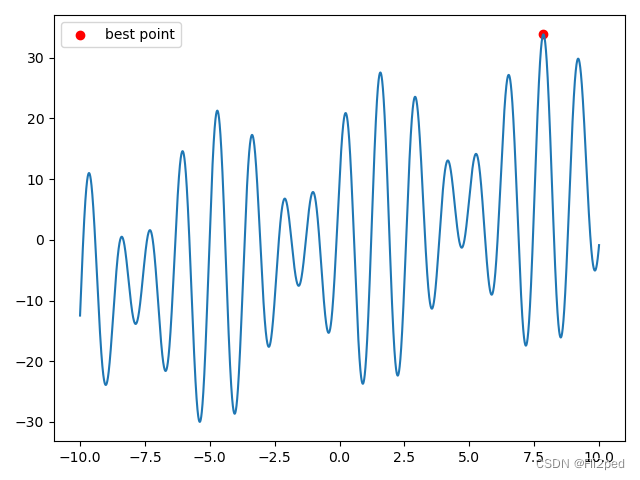
print(best_x)x = np.linspace(-10, 10, 100000)def fun(x):return x + 16 * np.sin(5 * x) + 10 * np.cos(4 * x)
y=fun(x)
plt.plot(x, y)plt.scatter(best_x,best_y,c='r',label='best point')
plt.legend()
plt.show()
注:
算法思想和matlab代码来自于
【通俗易懂讲算法-最优化之粒子群优化(PSO)】
python代码来自于
粒子群PSO优化算法学习笔记 及其python实现(附讲解如何使用python语言sko.PSO工具包)
相关文章:

PSO粒子群优化算法
PSO粒子群优化算法 算法思想matlab代码python代码 算法思想 粒子群算法(Particle Swarm Optimization) 优点: 1)原理比较简单,实现容易,参数少。 缺点: 1)易早熟收敛至局部最优、迭代后期收敛速度慢的…...
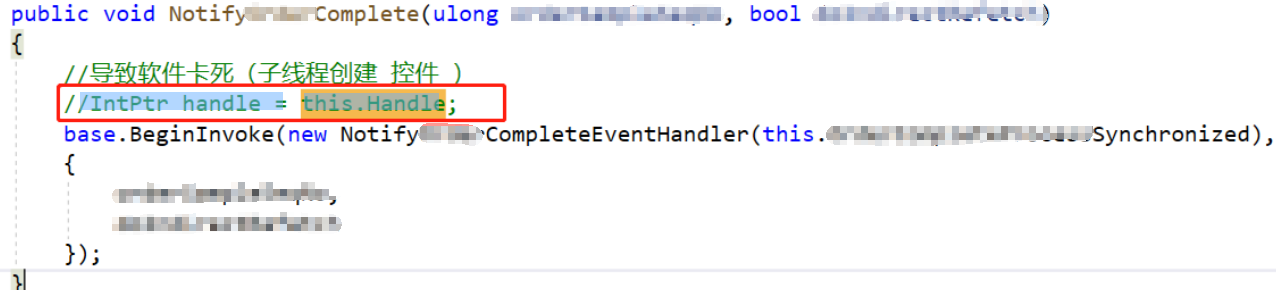
记一次 .NET某医疗器械清洗系统 卡死分析
一:背景 1. 讲故事 前段时间协助训练营里的一位朋友分析了一个程序卡死的问题,回过头来看这个案例比较经典,这篇稍微整理一下供后来者少踩坑吧。 二:WinDbg 分析 1. 为什么会卡死 因为是窗体程序,理所当然就是看主…...

C# 基于Rijndael对文件进行加解密
介绍: Rijndael 是一种对称加密算法,也是 AES(Advanced Encryption Standard)的前身。它用于数据的加密和解密,并提供了安全且高效的加密功能。 在.NET Framework 中,Rijndael 类是一个实现了 Rijndael 算法…...
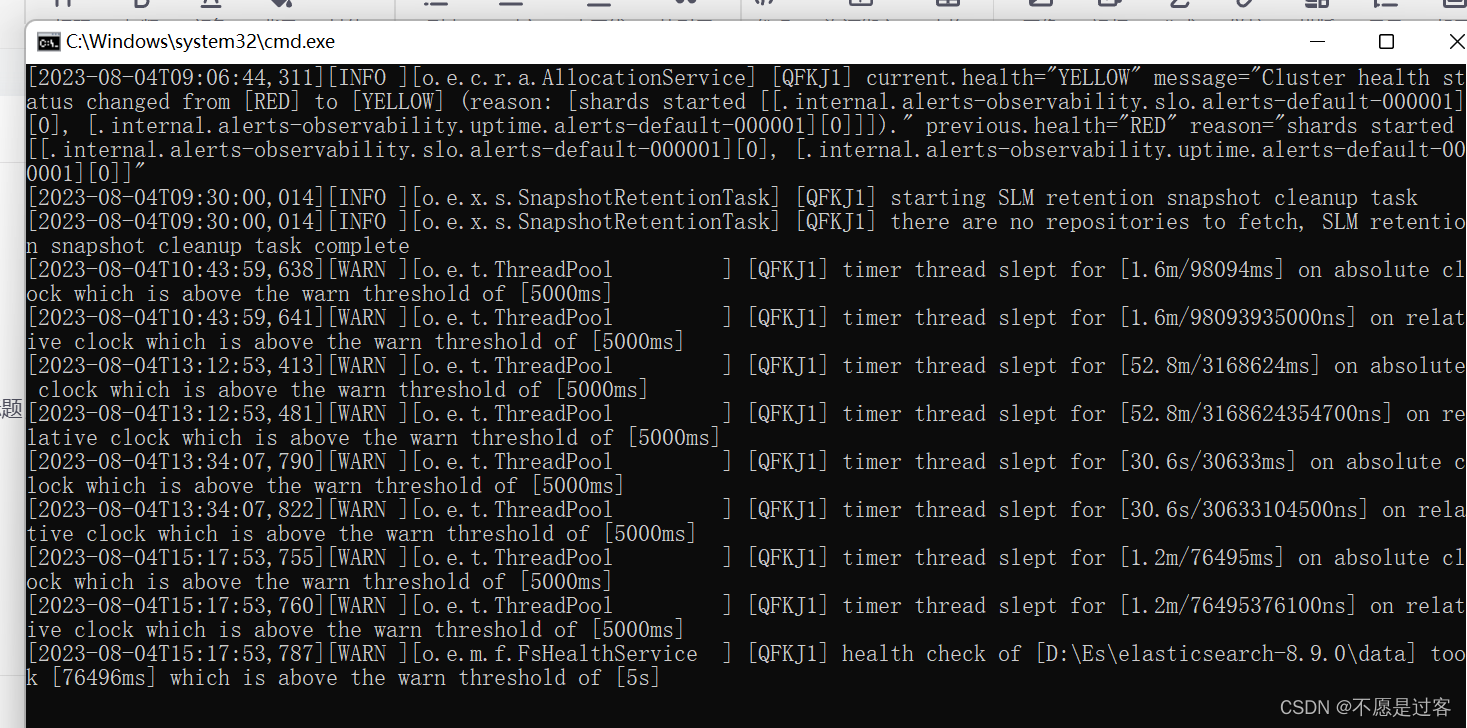
Elasticsearchr入门
首先在官网下载elasticsearch8.9版本,以及8.9版本的kibana。 解压,点击es8.9bin目录下的elasticsearch.bat文件启动es 如图所示即为成功。 启动之后打开idea,添加依赖 <dependency><groupId>com.fasterxml.jackson.core</g…...
)
【ARM】imx6ul移植kernel记录,恩智浦github提供的最新kernel(2023年7月31)
❤️作者主页:凉开水白菜 ❤️作者简介:共同学习,互相监督,热于分享,多加讨论,一起进步! ❤️专栏目录: ❤️专栏资料: ❤️点赞 👍 收藏 ⭐再看,养成习惯 订阅的粉丝可通过PC端文末加我微信,可对文章的内容进行一对一答疑! 文章目录 一、简介二、源码下载三、官方…...
eeglab(自用)
目录 1.加载、显示数据 2.绘制脑电头皮图 3.绘制通道光谱图 4.预处理工具 5.ICA去除伪迹 5. 提取数据epoch 1.加载、显示数据 观察事件值(Event values):该数据集中包含2400个事件,每个事件指定了EEG.event结构的字段Type(类型)、position(位置)和…...
Dockerfile构建Tomcat镜像(源码)
Dockerfile构建Tomcat镜像 目录 Dockerfile构建Tomcat镜像 1、建立工作目录 2、编写Dockerfile文件 3、构建镜像 4、测试容器 5、浏览器访问测试: 1、建立工作目录 [roothuyang1 ~]# mkdir tomcat[roothuyang1 ~]# cd tomcat/[roothuyang1 tomcat]# lsapach…...
: has more than one overload的解决方法)
Frida Error: getPackageInfoNoCheck(): has more than one overload的解决方法
使用frida绕过证书的时候执行代码: frida -U -f de.robv.android.xposed.installer --codeshare akabe1/frida-multiple-unpinning --no-pause遇到这样的错误 Error: getPackageInfoNoCheck(): has more than one overload, use .overload() to choose from: 网上查…...

flutter开发实战-RawKeyboardListener监听键盘事件及keycode。
flutter开发实战-RawKeyboardListener监听键盘事件及keycode。 最近开发过程中遇到外设备的按钮点击触发相应的操作,需要监听对应的keycode来开启游戏或者相关操作。 这里用到了RawKeyboardListener 一、RawKeyboardListener是什么? RawKeyboardListe…...

Temu、希音们全托管引争议,跨境电商应变“工贸一体化”
自7月27日Shopee宣布正式上线全托管模式起,全托管似乎突然又进入了爆发期。 在7月31日至8月1日举行的2023第八届深圳国际跨境电商贸易博览会上,全托管成为SHEIN、Wish、Lazada等平台力推的运营模式。进入8月,跨境圈突然涌现大批传言称&#…...
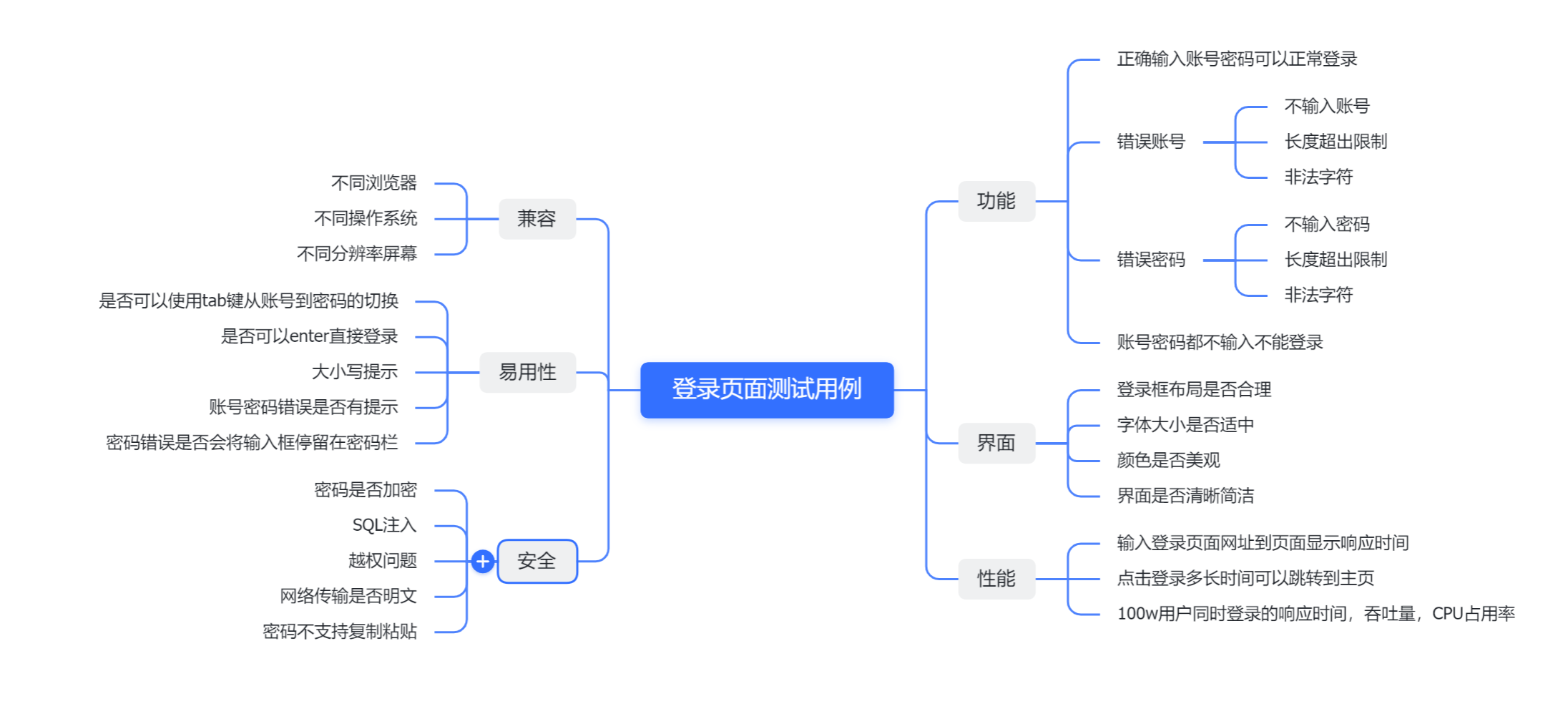
某科技公司提前批测试岗
文章目录 题目 今天给大家带来一家提前批测试岗的真题,目前已经发offer 题目 1.自我介绍 2.登录页面测试用例设计 3.如何模拟多用户登录 可以使用Jmeter,loadRunner性能测试工具来模拟大量用户登录操作去观察一些参数变化 4.有使用过Jmeter,loadRunner做过性能压…...
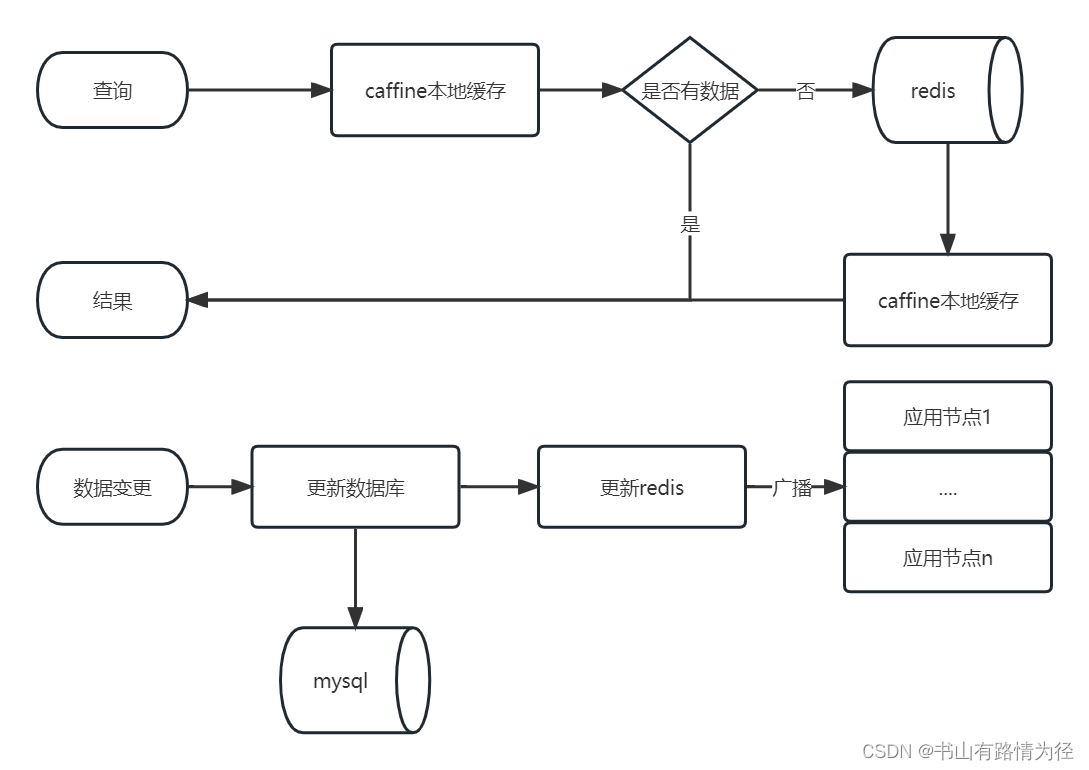
一次redis缓存不均衡优化经验
背景 高并发接口,引入redis作为缓存之后,运行一段时间发现redis各个节点在高峰时段的访问量严重不均衡,有的节点访问量7000次/s,有的节点访问量500次/s 此种现象虽然暂时不影响系统使用,但是始终是个安全隐患&#x…...

npm发布包
1.npm 登录 在控制台输入命令 npm login 按提示输入用户名,密码,邮箱后登录 如果出现如下提示 需要将淘宝镜像源切换为npm源,删除或注释以下内容就行 2.发布 进入准备发布的代码的根目录下,输入命令 npm publish 3.删除已发…...
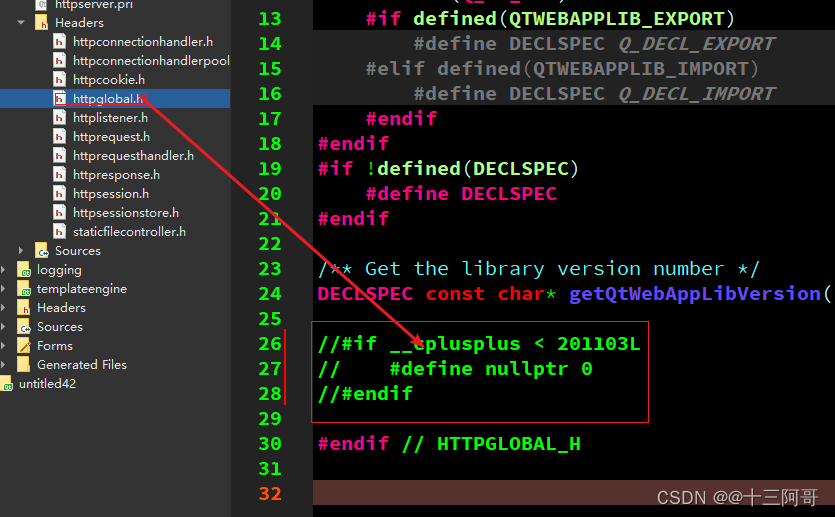
Qt5.13引入QtWebApp的模块后报错: error C2440: “reinterpret_cast”: 无法从“int”转换为“quintptr”
1、开发环境 Win10-64 qt5.13 msvc2015-64bit-release 2、报错 新建一个demo工程。 引入QtWebApp的httpserver、logging、templateengine三个模块后。 直接运行,,此时报错如下: E:\Qt5.13.1\install\5.13.1\msvc2015_64\include\QtCore…...

软件为什么要进行性能压力测试?
软件为什么要进行性能压力测试?随着软件应用的不断增多和复杂度的提高,软件的性能对用户体验和业务成功至关重要。性能问题可能导致软件运行缓慢、崩溃或无响应,给用户带来不便甚至损失。为了确保软件能够在高负载和压力下正常运行࿰…...
阻塞队列BlockingQueue详解
一、阻塞队列介绍 1、队列 队列入队从队首开始添加,直至队尾;出队从队首出队,直至队尾,所以入队和出队的顺序是一样的 Queue接口 add(E) :在指定队列容量条件下添加元素,若成功返回true,若当前…...
pygame贪吃蛇游戏
pygame贪吃蛇游戏 贪吃蛇游戏通过enter键启动,贪吃蛇通过WSAD进行上下左右移动,每次在游戏区域中随机生成一个食物,每次吃完食物后,蛇变长并且获得积分;按空格键暂停。 贪吃蛇 import random, sys, time, pygame from …...

Mac系统下使用远程桌面连接Windows系统
一、远程桌面工具 Microsoft Remote Desktop 二、下载地址 https://go.microsoft.com/fwlink/?linkid868963 三、下载并安装 四、添加远程PC PC name:云服务器IP。 User account: 添加系统用户 PC name:远程桌面 IP 地址User account:可以选择是…...

使用 OpenCV 和深度学习对黑白图像进行着色
在本文中,我们将创建一个程序将黑白图像(即灰度图像)转换为彩色图像。我们将为此程序使用 Caffe 着色模型。您应该熟悉基本的 OpenCV 功能和用法,例如读取图像或如何使用 dnn 模块加载预训练模型等。现在让我们讨论实现该程序所遵循的过程。 给定一张灰度照片作为输入,本文…...

从价值的角度看,为何 POSE 通证值得长期看好
PoseSwap 是 Nautilus Chain 上的首个 DEX,基于 Nautilus Chain 也让其成为了首个以模块化构建的 Layer3 架构的 DEX。该 DEX 本身能够以 Dapp 层(Rollup)的形态,与其他应用层并行化运行。...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...
