【LeetCode 算法】Power of Heroes 英雄的力量
文章目录
- Power of Heroes 英雄的力量
- 问题描述:
- 分析
- 代码
- Tag
Power of Heroes 英雄的力量
问题描述:
给你一个下标从 0 开始的整数数组 nums ,它表示英雄的能力值。如果我们选出一部分英雄,这组英雄的 力量 定义为:
i 0 , i 1 , . . . i k i_0 ,i_1 ,... i_k i0,i1,...ik 表示这组英雄在数组中的下标。那么这组英雄的力量为 m a x ( n u m s [ i 0 ] , n u m s [ i 1 ] . . . n u m s [ i k ] ) 2 ∗ m i n ( n u m s [ i 0 ] , n u m s [ i 1 ] . . . n u m s [ i k ] ) max(nums[i_0],nums[i_1] ... nums[i_k])2 * mi_n(nums[i_0],nums[i_1] ... nums[i_k]) max(nums[i0],nums[i1]...nums[ik])2∗min(nums[i0],nums[i1]...nums[ik]) 。
请你返回所有可能的 非空 英雄组的 力量 之和。由于答案可能非常大,请你将结果对 10^9 + 7 取余。
1 < = n u m s . l e n g t h < = 1 0 5 1 < = n u m s [ i ] < = 1 0 9 1 <= nums.length <= 10^5\\ 1 <= nums[i] <= 10^9 1<=nums.length<=1051<=nums[i]<=109
分析
一次周赛的hard,当时没时间做。
一开始没看清问题的意思,以为要计算子数组,而实际上是要求子集。
子集也可以认为是原数组的一个子序列,虽然这个说法不是很严谨。
假如有一个子序列,这个子序列的 p o w e r power power就是 m a x ∗ m a x ∗ m i n max*max*min max∗max∗min.
暴力
如果是使用暴力的方式,就是枚举所有的子序列然后对每个子序列进行找 m a x , m i n max,min max,min。
以当前数组的规模,可能有 2 100000 2^{100000} 2100000个子序列,很明显这样不可能,即使可以枚举出所有的子序列,在计算power的过程中的时间复杂度也是 O ( L ) O(L) O(L),和子序列的长度有关。
既然是找最大和最小,那就先排序,从小到大。因为是找子序列,所以排个序,不会影响最终结果。
假设区间 [ j , i ] , i > j [j,i],i>j [j,i],i>j,那么必然 a [ i ] > = a [ j ] a[i]>=a[j] a[i]>=a[j],此时以 a [ i ] a[i] a[i]为最大的子序列,就可以计算出来,即 2 i 2^i 2i个,从左向右计算:
- a [ 0 ] a[0] a[0]为 m i n min min时,可以与 a [ i ] a[i] a[i]构造的序列数量为 2 i − 1 2^{i-1} 2i−1,它们可以为最终的ans提供 a [ 0 ] ∗ a [ i ] ∗ 2 i − 1 a[0]*a[i]*2^{i-1} a[0]∗a[i]∗2i−1.
同理可以计算得到
- a [ 1 ] ∗ a [ i ] ∗ 2 i − 2 a[1]*a[i]*2^{i-2} a[1]∗a[i]∗2i−2.
- a [ 2 ] ∗ a [ i ] ∗ 2 i − 3 a[2]*a[i]*2^{i-3} a[2]∗a[i]∗2i−3.
- a [ 3 ] ∗ a [ i ] ∗ 2 i − 4 a[3]*a[i]*2^{i-4} a[3]∗a[i]∗2i−4.
… - a [ i − 2 ] ∗ a [ i ] ∗ 2 i − 1 − i + 2 a[i-2]*a[i]*2^{i-1-i+2} a[i−2]∗a[i]∗2i−1−i+2
- a [ i − 1 ] ∗ a [ i ] ∗ 2 i − 1 − i + 1 a[i-1]*a[i]*2^{i-1-i+1} a[i−1]∗a[i]∗2i−1−i+1
最后还要补一个 a [ i ] 3 a[i]^3 a[i]3,单个的也要算。
到此以a[i]为最大的所有子序列的power都可以计算出。
p [ i ] = a [ i ] 3 + a [ 0 ] ∗ a [ i ] ∗ 2 i − 1 + a [ 1 ] ∗ a [ i ] ∗ 2 i − 2 + . . + a [ i − 1 ] ∗ a [ i ] ∗ 2 i − 1 − i + 1 p [ i ] = a [ i ] ∗ ( a [ i ] 2 + a [ 0 ] ∗ 2 i − 1 + a [ 1 ] ∗ 2 i − 2 + . . + a [ i − 1 ] ∗ 2 i − 1 − i + 1 ) p[i] = a[i]^3 +a[0]*a[i]*2^{i-1} + a[1]*a[i]*2^{i-2} +.. + a[i-1]*a[i]*2^{i-1-i+1}\\ p[i] = a[i]*( a[i]^2 + a[0]*2^{i-1}+ a[1]*2^{i-2} + ..+ a[i-1]*2^{i-1-i+1}) p[i]=a[i]3+a[0]∗a[i]∗2i−1+a[1]∗a[i]∗2i−2+..+a[i−1]∗a[i]∗2i−1−i+1p[i]=a[i]∗(a[i]2+a[0]∗2i−1+a[1]∗2i−2+..+a[i−1]∗2i−1−i+1)
如果此时让k = i+1,即右移一位
p [ k ] = a [ k ] ∗ ( a [ k ] 2 + a [ 0 ] ∗ 2 i − 1 ∗ 2 + a [ 1 ] ∗ 2 i − 2 ∗ 2 + . . + a [ i − 1 ] ∗ 2 i − 1 − i + 1 ∗ 2 + a [ i ] ) p[k] = a[k]*( a[k]^2 + a[0]*2^{i-1}*2+ a[1]*2^{i-2}*2 + ..+ a[i-1]*2^{i-1-i+1}*2 + a[i])\\ p[k]=a[k]∗(a[k]2+a[0]∗2i−1∗2+a[1]∗2i−2∗2+..+a[i−1]∗2i−1−i+1∗2+a[i])
由于右端点的移动,新增了1位a[k],导致一部分同时乘2。
假设计算下标 i i i时 令 S i = a [ 0 ] ∗ 2 i − 1 + a [ 1 ] ∗ 2 i − 2 + . . + a [ i − 1 ] ∗ 2 i − 1 − i + 1 S_i = a[0]*2^{i-1}+ a[1]*2^{i-2} + ..+ a[i-1]*2^{i-1-i+1} Si=a[0]∗2i−1+a[1]∗2i−2+..+a[i−1]∗2i−1−i+1
那么 p [ i ] = a [ i ] ∗ ( a [ i ] 2 + S i ) p[i] = a[i]*( a[i]^2 + S_i) p[i]=a[i]∗(a[i]2+Si)
而当计算下标 k k k时,不需要重复计算 这一部分S,而是可以通过前一个i的S,来计算出当前所需要的 S k S_k Sk。
S k = 2 ∗ S i + a [ i − 1 ] S_k= 2*S_i + a[i-1] Sk=2∗Si+a[i−1]
p [ k ] = a [ k ] ∗ ( a [ k ] 2 + S k ) ; p[k] = a[k]*( a[k]^2 + S_k); p[k]=a[k]∗(a[k]2+Sk);
计算过程中还需要注意取余
代码
Math
class Solution {long MOD = (long)1e9+7;public int sumOfPower(int[] nums) { Arrays.sort(nums);long sum = 0,s = 0;int n = nums.length; for(int i=0;i<n;i++){long cur = ((long)nums[i])%MOD;long pow = (cur*cur)%MOD; sum = (sum + (pow*((cur +s)%MOD))%MOD)%MOD;s = ( 2*s + cur)%MOD; }return (int)sum;}
}
时间复杂度 O ( N L o g N ) O(NLogN) O(NLogN)
空间复杂度 O ( L o g N ) O(LogN) O(LogN)
Tag
Array
Math
Sort
相关文章:

【LeetCode 算法】Power of Heroes 英雄的力量
文章目录 Power of Heroes 英雄的力量问题描述:分析代码Math Tag Power of Heroes 英雄的力量 问题描述: 给你一个下标从 0 开始的整数数组 nums ,它表示英雄的能力值。如果我们选出一部分英雄,这组英雄的 力量 定义为ÿ…...

合宙Air724UG LuatOS-Air script lib API--ntp
ntp Table of Contents ntp ntp.timeSync(period, fnc, fun) ntp 模块功能:网络授时. 重要提醒!!!!!! 本功能模块采用多个免费公共的NTP服务器来同步时间 并不能保证任何时间任何地点都能百分…...
LangChain+ChatGLM大模型应用落地实践(一)
LLMs的落地框架(LangChain),给LLMs套上一层盔甲,快速构建自己的新一代人工智能产品。 一、简介二、LangChain源码三、租用云服务器实例四、部署实例 一、简介 LangChain是一个近期非常活跃的开源代码库,目前也还在快速…...
PSO粒子群优化算法
PSO粒子群优化算法 算法思想matlab代码python代码 算法思想 粒子群算法(Particle Swarm Optimization) 优点: 1)原理比较简单,实现容易,参数少。 缺点: 1)易早熟收敛至局部最优、迭代后期收敛速度慢的…...
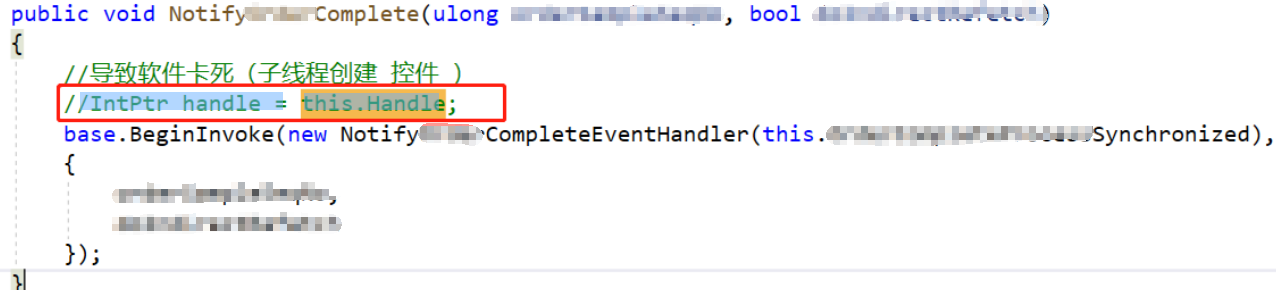
记一次 .NET某医疗器械清洗系统 卡死分析
一:背景 1. 讲故事 前段时间协助训练营里的一位朋友分析了一个程序卡死的问题,回过头来看这个案例比较经典,这篇稍微整理一下供后来者少踩坑吧。 二:WinDbg 分析 1. 为什么会卡死 因为是窗体程序,理所当然就是看主…...

C# 基于Rijndael对文件进行加解密
介绍: Rijndael 是一种对称加密算法,也是 AES(Advanced Encryption Standard)的前身。它用于数据的加密和解密,并提供了安全且高效的加密功能。 在.NET Framework 中,Rijndael 类是一个实现了 Rijndael 算法…...
Elasticsearchr入门
首先在官网下载elasticsearch8.9版本,以及8.9版本的kibana。 解压,点击es8.9bin目录下的elasticsearch.bat文件启动es 如图所示即为成功。 启动之后打开idea,添加依赖 <dependency><groupId>com.fasterxml.jackson.core</g…...
)
【ARM】imx6ul移植kernel记录,恩智浦github提供的最新kernel(2023年7月31)
❤️作者主页:凉开水白菜 ❤️作者简介:共同学习,互相监督,热于分享,多加讨论,一起进步! ❤️专栏目录: ❤️专栏资料: ❤️点赞 👍 收藏 ⭐再看,养成习惯 订阅的粉丝可通过PC端文末加我微信,可对文章的内容进行一对一答疑! 文章目录 一、简介二、源码下载三、官方…...
eeglab(自用)
目录 1.加载、显示数据 2.绘制脑电头皮图 3.绘制通道光谱图 4.预处理工具 5.ICA去除伪迹 5. 提取数据epoch 1.加载、显示数据 观察事件值(Event values):该数据集中包含2400个事件,每个事件指定了EEG.event结构的字段Type(类型)、position(位置)和…...
Dockerfile构建Tomcat镜像(源码)
Dockerfile构建Tomcat镜像 目录 Dockerfile构建Tomcat镜像 1、建立工作目录 2、编写Dockerfile文件 3、构建镜像 4、测试容器 5、浏览器访问测试: 1、建立工作目录 [roothuyang1 ~]# mkdir tomcat[roothuyang1 ~]# cd tomcat/[roothuyang1 tomcat]# lsapach…...
: has more than one overload的解决方法)
Frida Error: getPackageInfoNoCheck(): has more than one overload的解决方法
使用frida绕过证书的时候执行代码: frida -U -f de.robv.android.xposed.installer --codeshare akabe1/frida-multiple-unpinning --no-pause遇到这样的错误 Error: getPackageInfoNoCheck(): has more than one overload, use .overload() to choose from: 网上查…...

flutter开发实战-RawKeyboardListener监听键盘事件及keycode。
flutter开发实战-RawKeyboardListener监听键盘事件及keycode。 最近开发过程中遇到外设备的按钮点击触发相应的操作,需要监听对应的keycode来开启游戏或者相关操作。 这里用到了RawKeyboardListener 一、RawKeyboardListener是什么? RawKeyboardListe…...

Temu、希音们全托管引争议,跨境电商应变“工贸一体化”
自7月27日Shopee宣布正式上线全托管模式起,全托管似乎突然又进入了爆发期。 在7月31日至8月1日举行的2023第八届深圳国际跨境电商贸易博览会上,全托管成为SHEIN、Wish、Lazada等平台力推的运营模式。进入8月,跨境圈突然涌现大批传言称&#…...
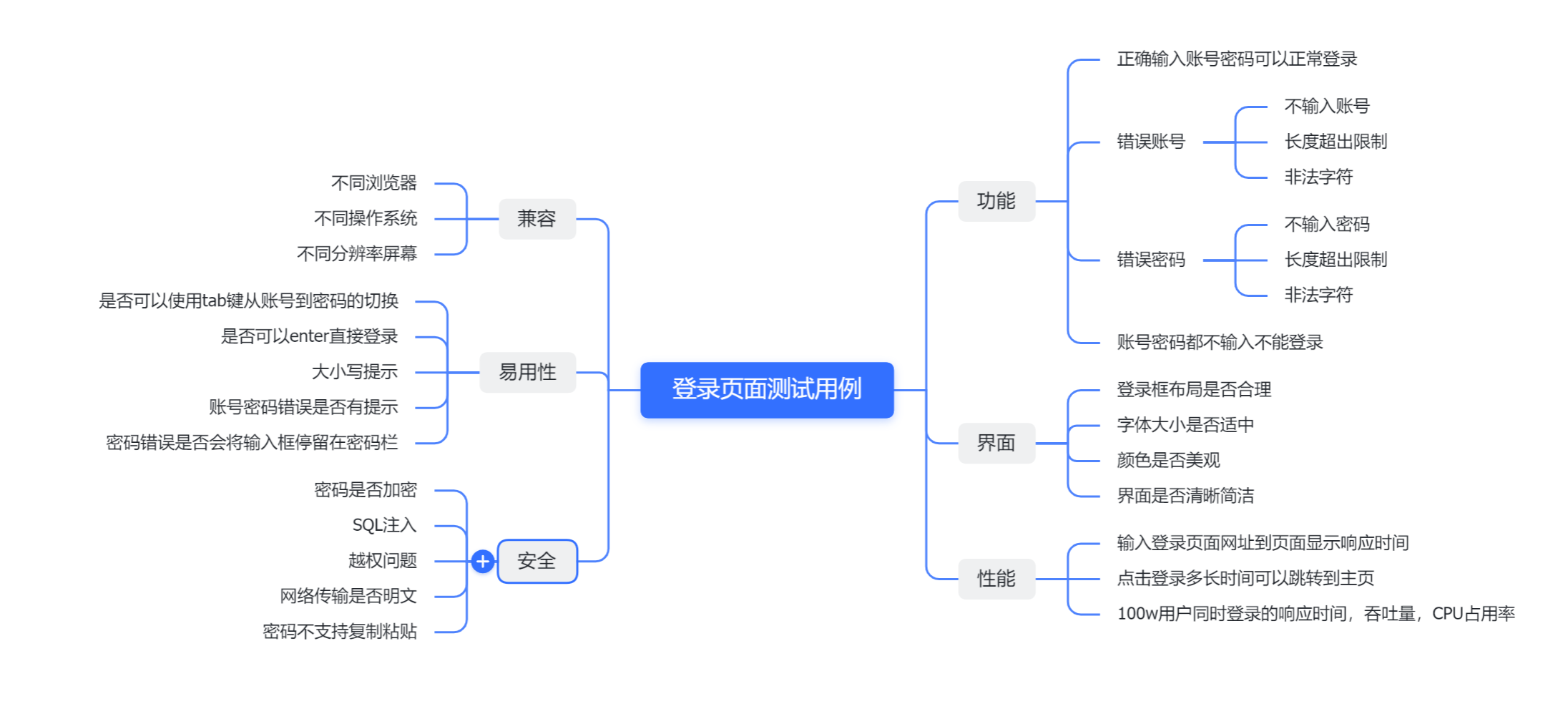
某科技公司提前批测试岗
文章目录 题目 今天给大家带来一家提前批测试岗的真题,目前已经发offer 题目 1.自我介绍 2.登录页面测试用例设计 3.如何模拟多用户登录 可以使用Jmeter,loadRunner性能测试工具来模拟大量用户登录操作去观察一些参数变化 4.有使用过Jmeter,loadRunner做过性能压…...
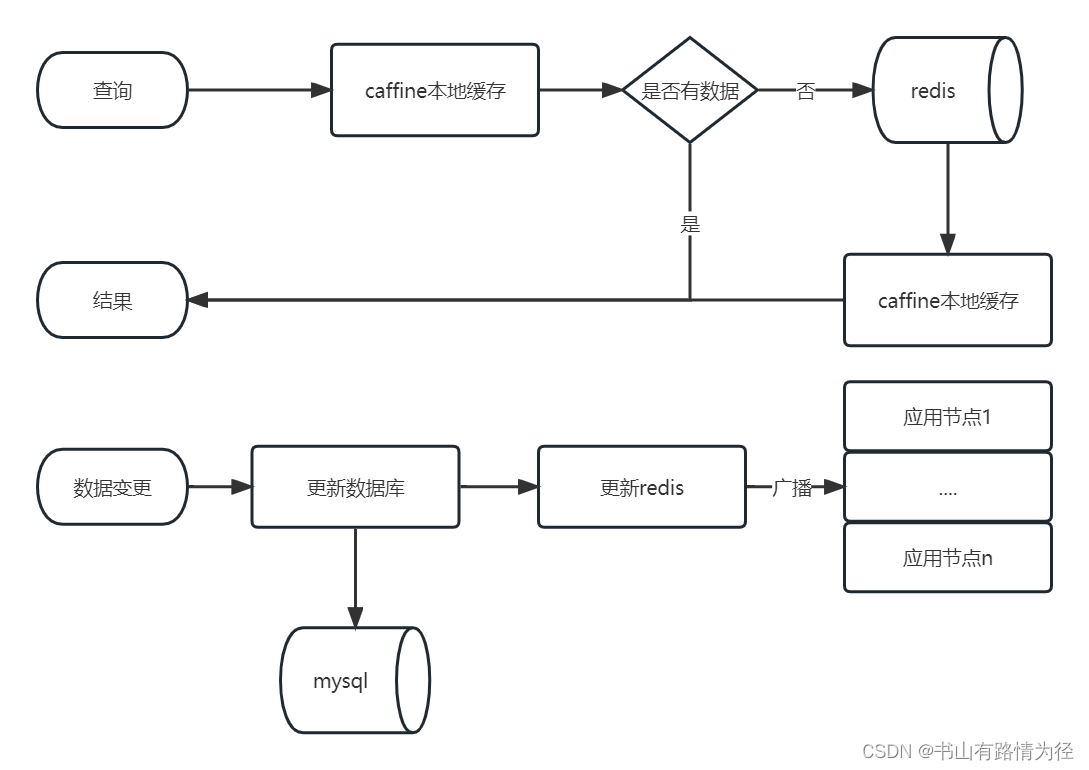
一次redis缓存不均衡优化经验
背景 高并发接口,引入redis作为缓存之后,运行一段时间发现redis各个节点在高峰时段的访问量严重不均衡,有的节点访问量7000次/s,有的节点访问量500次/s 此种现象虽然暂时不影响系统使用,但是始终是个安全隐患&#x…...

npm发布包
1.npm 登录 在控制台输入命令 npm login 按提示输入用户名,密码,邮箱后登录 如果出现如下提示 需要将淘宝镜像源切换为npm源,删除或注释以下内容就行 2.发布 进入准备发布的代码的根目录下,输入命令 npm publish 3.删除已发…...
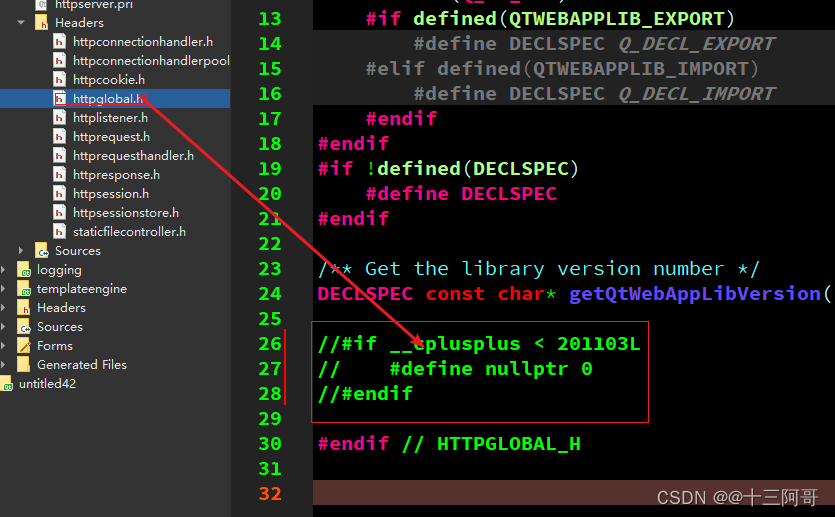
Qt5.13引入QtWebApp的模块后报错: error C2440: “reinterpret_cast”: 无法从“int”转换为“quintptr”
1、开发环境 Win10-64 qt5.13 msvc2015-64bit-release 2、报错 新建一个demo工程。 引入QtWebApp的httpserver、logging、templateengine三个模块后。 直接运行,,此时报错如下: E:\Qt5.13.1\install\5.13.1\msvc2015_64\include\QtCore…...

软件为什么要进行性能压力测试?
软件为什么要进行性能压力测试?随着软件应用的不断增多和复杂度的提高,软件的性能对用户体验和业务成功至关重要。性能问题可能导致软件运行缓慢、崩溃或无响应,给用户带来不便甚至损失。为了确保软件能够在高负载和压力下正常运行࿰…...
阻塞队列BlockingQueue详解
一、阻塞队列介绍 1、队列 队列入队从队首开始添加,直至队尾;出队从队首出队,直至队尾,所以入队和出队的顺序是一样的 Queue接口 add(E) :在指定队列容量条件下添加元素,若成功返回true,若当前…...
pygame贪吃蛇游戏
pygame贪吃蛇游戏 贪吃蛇游戏通过enter键启动,贪吃蛇通过WSAD进行上下左右移动,每次在游戏区域中随机生成一个食物,每次吃完食物后,蛇变长并且获得积分;按空格键暂停。 贪吃蛇 import random, sys, time, pygame from …...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...
