【深度学习_TensorFlow】梯度下降
写在前面
一直不太理解梯度下降算法是什么意思,今天我们就解开它神秘的面纱
写在中间
线性回归方程
如果要求出一条直线,我们只需知道直线上的两个不重合的点,就可以通过解方程组来求出直线
但是,如果我们选取的这两个点不在直线上,而是存在误差(暂且称作观测误差),这样求出的直线就会和原直线相差很大,我们应该怎样做呢?首先肯定不能只通过两个点,就武断地求出这条直线。

我们通常尽可能多地使用分布在直线周围的点,也可能不存在一条直线完美的穿过所有采样点。那么,退而求其次,我们希望能找到一条比较“好”的位于采样点中间的直线。那么怎么衡量“好”与“不好”呢?一个很自然的想法就是,求出当前模型的所有采样点上的预测值𝑤𝑥(𝑖) + 𝑏与真实值𝑦(𝑖)之间的差的平方和作为总误差 L \mathcal{L} L,然后搜索一组参数 w ∗ , b ∗ w^{*},b^{*} w∗,b∗使得 L \mathcal{L} L最小,对应的直线就是我们要寻找的最优直线。
w ∗ , b ∗ = arg min w , b 1 n ∑ i = 1 n ( w x ( i ) + b − y ( i ) ) 2 w^*,b^*=\arg\min_{w,b}\frac{1}{n}\sum_{i=1}^{n}\bigl(wx^{(i)}+b-y^{(i)}\bigr)^2 w∗,b∗=argminw,bn1∑i=1n(wx(i)+b−y(i))2
最后再通过梯度下降法来不断优化参数 w ∗ , b ∗ w^{*},b^{*} w∗,b∗
有基础的小伙伴们可能知道求误差的方法其实就是均方误差函数,不懂得可以看这篇文章补充养分《误差函数》 ,我们这篇文章就侧重梯度下降。
梯度下降
函数的梯度定义为函数对各个自变量的偏导数组成的向量。不会的话,翻翻高等数学下册书。
举个例子,对于曲面函数𝑧 = 𝑓(𝑥, 𝑦),函数对自变量𝑥的偏导数记为 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z,函数对自变量𝑦的偏导数记为 ∂ z ∂ y \frac{\partial z}{\partial y} ∂y∂z,则梯度∇𝑓为向量 ( ∂ z ∂ x , ∂ z ∂ y ) ({\frac{\partial z}{\partial x}},{\frac{\partial z}{\partial y}}) (∂x∂z,∂y∂z),梯度的方向总是指向当前位置函数值增速最大的方向,函数曲面越陡峭,梯度的模也越大。
函数在各处的梯度方向∇𝑓总是指向函数值增大的方向,那么梯度的反方向−∇𝑓应指向函数值减少的方向。利用这一性质,我们只需要按照下式来更新参数,,其中𝜂用来缩放梯度向量,一般设置为某较小的值,如 0.01、0.001 等。
x ′ = x − η ⋅ d y d x x'=x-\eta\cdot\frac{\mathrm{d}y}{\mathrm{d}x} x′=x−η⋅dxdy
结合上面的回归方程,我们就可对误差函数求偏导,以循环的方式更新参数 w , b w,b w,b:
w ′ = w − η ∂ L ∂ w b ′ = b − η ∂ L ∂ b \begin{aligned}w'&=w-\eta\frac{\partial\mathcal{L}}{\partial w}\\\\b'&=b-\eta\frac{\partial\mathcal{L}}{\partial b}\end{aligned} w′b′=w−η∂w∂L=b−η∂b∂L
函数实现
计算过程都需要包裹在 with tf.GradientTape() as tape 上下文中,使得前向计算时能够保存计算图信息,方便自动求导操作。通过tape.gradient()函数求得网络参数到梯度信息,结果保存在 grads 列表变量中。
GradientTape()函数
GradientTape(persistent=False, watch_accessed_variables=True)
-
persistent: 布尔值,用来指定新创建的gradient
tape是否是可持续性的。默认是False,意味着只能够调用一次GradientTape()函数,再次使用会报错 -
watch_accessed_variables:布尔值,表明GradientTape()函数是否会自动追踪任何能被训练的变量。默认是True。要是为False的话,意味着你需要手动去指定你想追踪的那些变量。
tape.watch()函数
tape.watch()用于跟踪指定类型的tensor变量。
- 由于GradientTape()默认只对
tf.Variable类型的变量进行监控。如果需要监控的变量是tensor类型,则需要tape.watch()来监控,否则输出结果将是None
tape.gradient()函数
tape.gradient(target, source)
-
target:求导的因变量 -
source:求导的自变量
import tensorflow as tfw = tf.constant(1.)
x = tf.constant(2.)
y = x * wwith tf.GradientTape() as tape:tape.watch([w])y = x * wgrads = tape.gradient(y, [w])
print(grads)
写在最后
👍🏻点赞,你的认可是我创作的动力!
⭐收藏,你的青睐是我努力的方向!
✏️评论,你的意见是我进步的财富!
相关文章:

【深度学习_TensorFlow】梯度下降
写在前面 一直不太理解梯度下降算法是什么意思,今天我们就解开它神秘的面纱 写在中间 线性回归方程 如果要求出一条直线,我们只需知道直线上的两个不重合的点,就可以通过解方程组来求出直线 但是,如果我们选取的这两个点不在直…...

C++使用 auto 自动推断类型
C使用 auto 自动推断类型 在有些情况下, 根据赋给变量的初值, 很容易知道其类型。 例如, 如果将变量的初值设置成了 true,就可推断其类型为 bool。如果您使用的编译器支持 C11 和更高版本,可不显式地指定变量的类型&a…...

【前端面试手撕题】call、bind、new、freeze、浅拷贝
FED11 _call函数 描述 请补全JavaScript代码,要求实现Function.call函数的功能且该新函数命名为"_call"。 <!DOCTYPE html> <html><head><meta charset"UTF-8"><style>/* 填写样式 */</style> </head…...
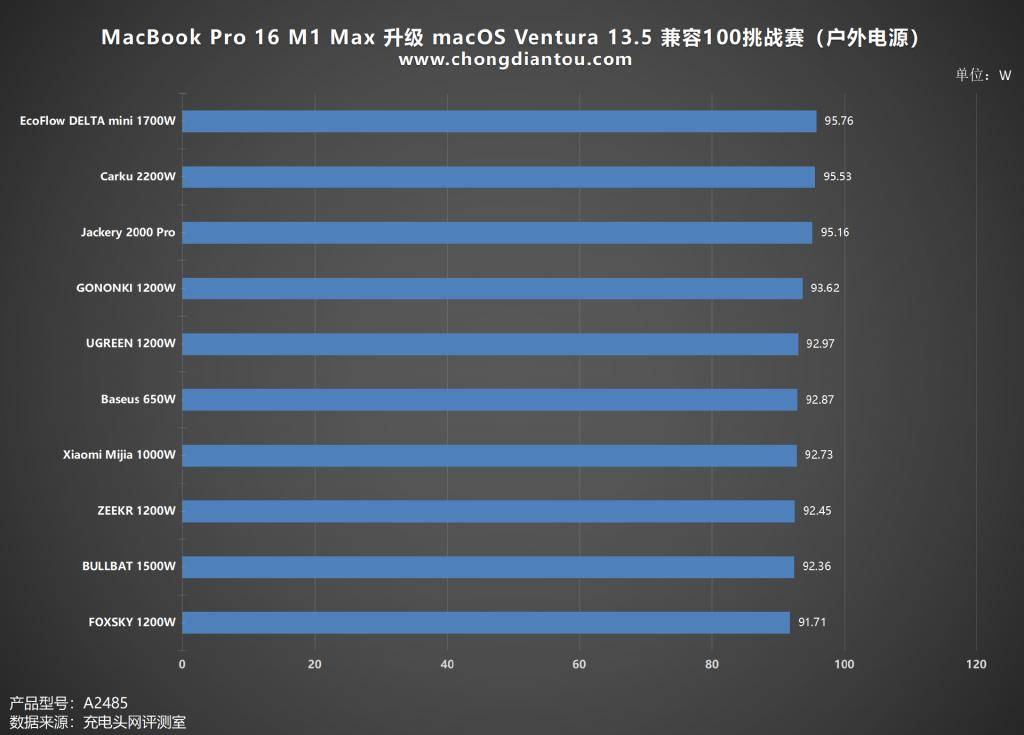
MacBook Pro 16 M1 Max 升级 macOS Ventura 13.5 兼容测评
今天给大家带来了 MacBook Pro 16 M1 Max 升级 macOS Ventura 13.5 兼容 100 挑战赛 的视频,现在充电头再以文章的形式呈现给大家,让大家更清楚、直白的了解这款笔记本在升级系统后的兼容性如何。 MacBook Pro 16 M1 Max 配置了 140W 的 MagSafe 充电口&…...
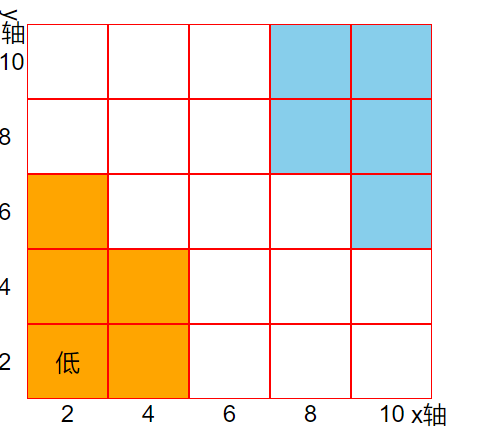
实现5*5正方形网格x轴和y轴显示对应数值组件封装
实现5*5正方形网格x轴和y轴显示对应数值组件封装 需求:按5*5的正方形网格,根据目标数据的x和y轴值显示对应的文字,实现效果图如下:(当前目标数值:x2,y2) 代码如下: <…...
)
基于Matlab实现图像压缩技术(附上完整源码+图像+程序运行说明)
介绍 图像压缩是一种将图像数据压缩以减小文件大小的技术。在数字图像处理中,图像通常以像素阵列的形式表示。对于大型图像文件,传输和存储成本可能很高,因此图像压缩技术变得至关重要。在本文中,我们将介绍一种使用Matlab实现图…...
棒球联盟对于市场发展规划·棒球1号位
棒球联盟对于市场发展规划 1. 棒球联盟市场发展背景分析 在深入探讨棒球联盟市场发展背景之前,我们首先要明确,棒球,作为一种全球流行的体育项目,其在市场上的发展具有相当悠久的历史。棒球文化的起源可以追溯到上个世纪初&#…...
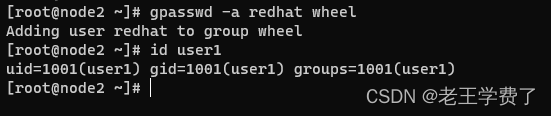
ansible控制主机和受控主机之间免密及提权案例
目录 案例描述 环境准备 案例一--免密远程控制主机 效果展示: 解决方案 1.添加主机 2.通过ssh-key生成密钥对 3.生成ssh-copy-id 4.验证 案例二-----免密普通用户提权 效果展示 解决方案 1.使用普通用户,与案例一 一样,进行发送密钥…...
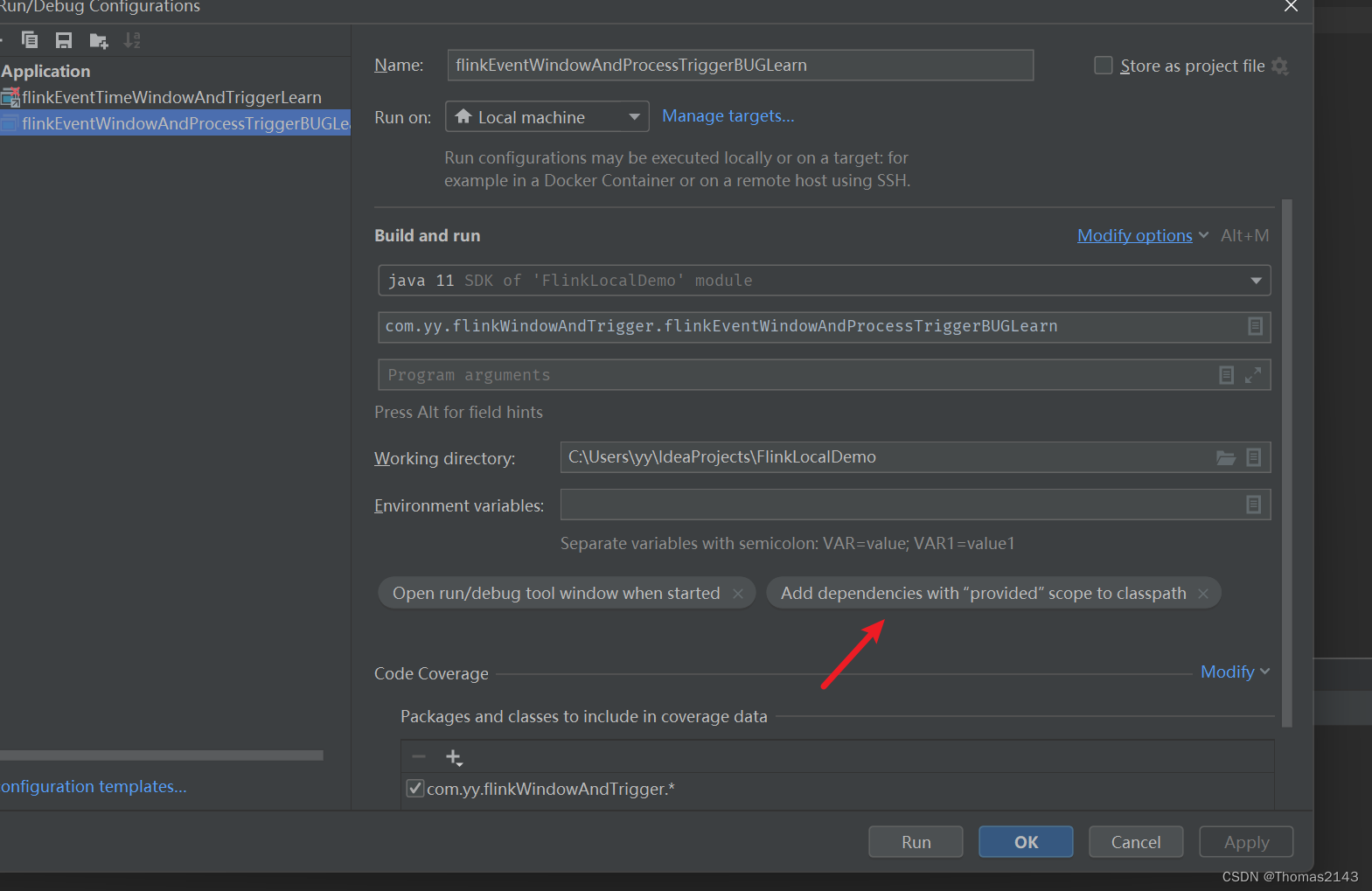
flink1.17 eventWindow不要配置processTrigger
理论上可以eventtime processtime混用,但是下面代码测试发现bug,输入一条数据会一直输出. flink github无法提bug/问题. apache jira账户新建后竟然flink又需要一个账户,放弃 bug复现操作 idea运行代码后 往source kafka发送一条数据 a,1,1690304400000 可以看到无限输出…...
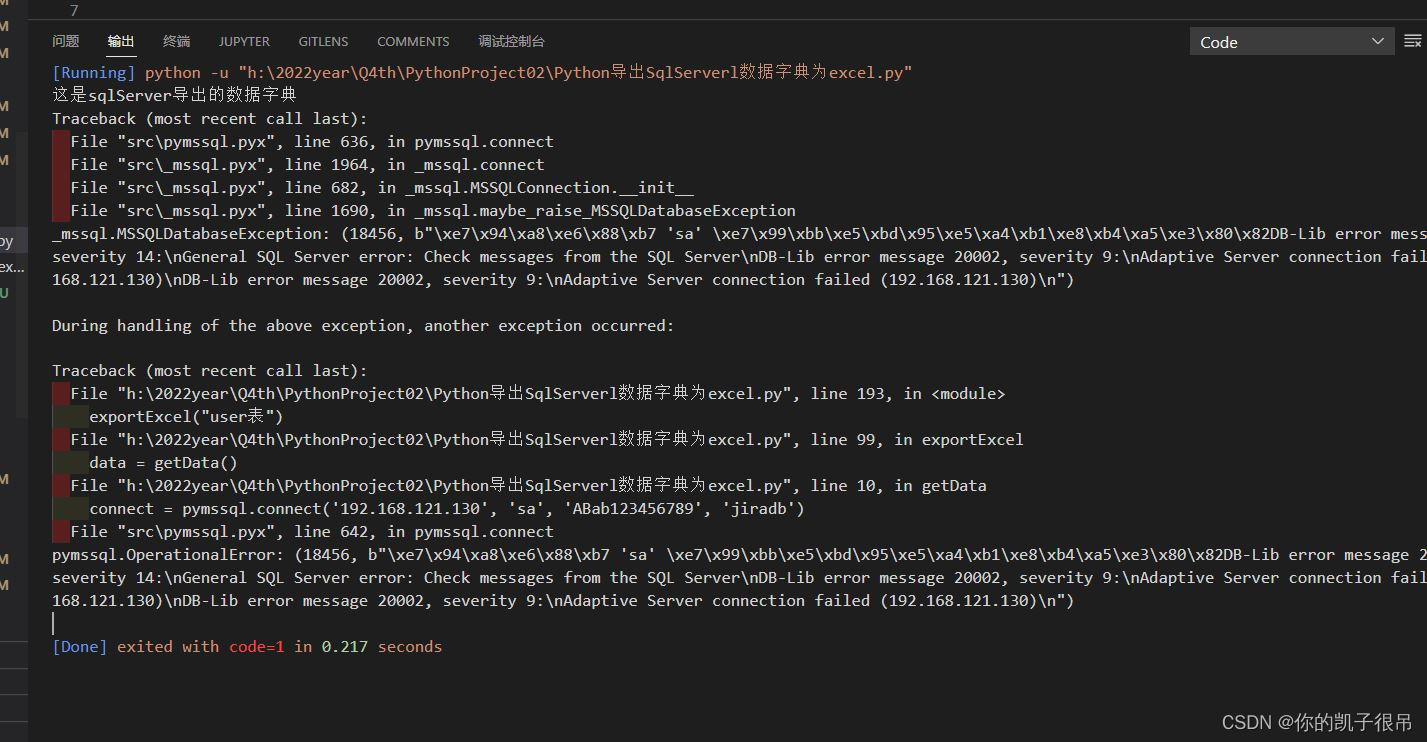
Python导出SqlServerl数据字典为excel
sql代码 SELECTtableName D.name ,tableIntroduce isnull(F.value, ),sort A.colorder,fieldName A.name,catogary B.name,bytes A.Length,lengths COLUMNPROPERTY(A.id, A.name, PRECISION),scales isnull(COLUMNPROPERTY(A.id, A.name, Scale), 0),isOrNotNull Cas…...

PB:DDE服务器函数
1、GetCommandDDE() 功 能:得到DDE客户应用发送的命令。 语 法:GetCommandDDE ( string ) 参 数:string:string类型的变量,用于保存DDE客户应用发送的命令。 返回值:Integer。函数执行成功时返回1,发生错误时返回-1。如果string参数的值为NULL, GetCommandDDE()…...

awk经典实战、正则表达式
目录 1.筛选给定时间范围内的日志 2.统计独立IP 案列 需求 代码 运行结果 3.根据某字段去重 案例 运行结果 4.正则表达式 1)认识正则 2)匹配字符 3)匹配次数 4)位置锚定:定位出现的位置 5)分组…...

Python脚本-时间盲注
BlindBool_get import requests from optparse import OptionParser import threading#存放变量 DBName "" DBTables [] DBColumns [] DBData {} flag You are in #设置重连次数以及将连接改为短连接 #防止因为HTTP连接数过多导致的MAX retries exceeded with …...

面试总结-Redis篇章(十)——Redis哨兵模式、集群脑裂
Redis哨兵模式、集群脑裂 哨兵模式哨兵的作用服务状态监控 Redis集群(哨兵模式)脑裂解决办法 哨兵模式 为了保证Redis的高可用,Redis提供了哨兵模式 哨兵的作用 服务状态监控 Redis集群(哨兵模式)脑裂 假设由于网络原…...

el-table那些事
el-table那些事 获取el-table所有勾选的行数据 用于记录工作和日常学习遇到的坑,需求。 vue3element-plusts 获取el-table所有勾选的行数据 1、需要先声明一个ref变量,并赋值给el-table 2、通过el-table提供的getSelectionRows()函数获取选中的"行…...
)
kubernetes(一)
文章目录 1. k8s架构2. k8s集群搭建 1. k8s架构 2. k8s集群搭建...
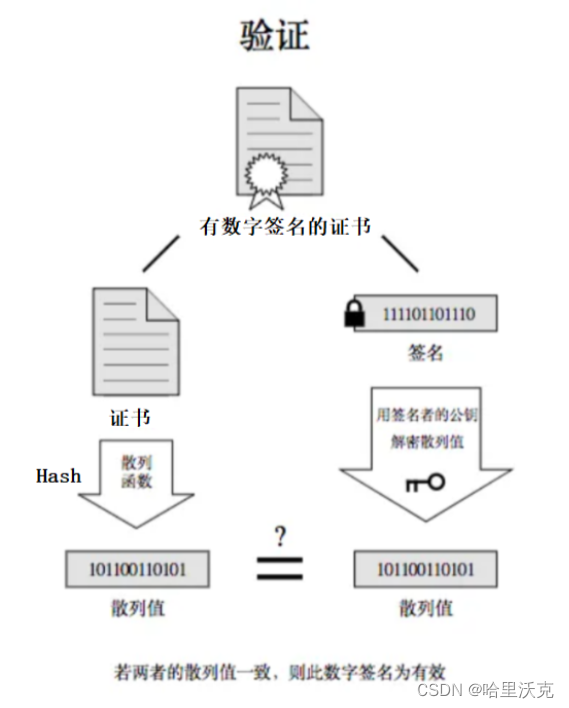
计算机网络(6) --- https协议
计算机网络(5) --- http协议_哈里沃克的博客-CSDN博客http协议https://blog.csdn.net/m0_63488627/article/details/132089130?spm1001.2014.3001.5501 目录 1.HTTPS的出现 1.HTTPS协议介绍 2.补充概念 1.加密 1.解释 2.原因 3.加密方式 对称加…...
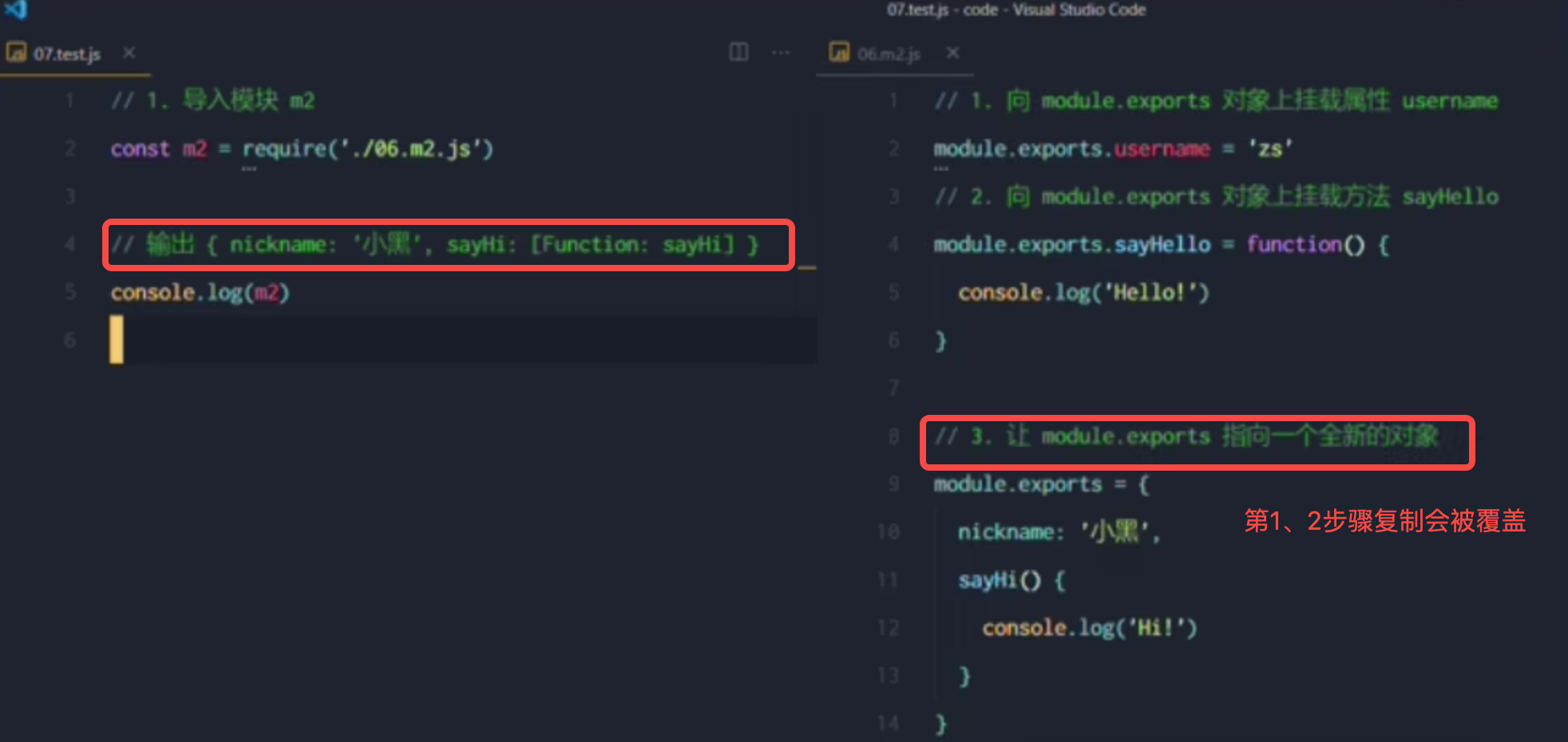
(三)Node.js - 模块化
1. Node.js中的模块化 Node.js中根据模块来源不同,将模块分为了3大类,分别是: 内置模块:内置模块由Node.js官方提供的,例如fs、path、http等自定义模块:用户创建的每个.js文件,都是自定义模块…...

502 bad gateway报错
代码在本地运行可以正常访问后端接口,部署服务器报错502。直接检查防火墙状态是否开启,先关闭防火墙试一下。如果是防火墙的原因在打开防火墙,开放需要的端口即可。 1、先查看防火墙状态: systemctl status firewalld2、停止防火…...

Flink学习教程
最近因为用到了Flink,所以博主开了《Flink教程》专栏来记录Flink的学习笔记。 【Apache Flink v1.16 中文文档】 【官网 - Apache Flink v1.3 中文文档】 一、基础 参考链接如下: Flink教程(01)- Flink知识图谱Flink教程&…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...
