解决:vue通过params传参刷新页面参数丢失问题以及实现vue路由可选参数的解决办法
目录
🙋♂️ 实现params传参,刷新页面不丢参
🙋♂️ 实现vue配置可选路由参数
🙋♂️ 参考资料

解决vue 通过 name 和 params 进行页面传参时,刷新页面参数丢失问题以及vue路由实现可选参数
🙋♂️ 实现params传参,刷新页面不丢参
路由配置文件——router.js:
export default new Router({routes: [{path: "/",redirect: "/main",},{path: "/main",name: "Main",component: () => import("@/views/Main.vue"),children: [{//path: '/testPage', //这种方式不配置参数名,页面刷新会丢失参数path: "/testPage/:aaa/:bbb", //这样通过name 和 params进行路由传参时,刷新页面就不会丢失参数aaa和bbb 了。name: "TestPage",component: () => import("@/views/TestPage/TestPage.vue"),},],},],
});调整函数:
methods: {//路由调整传参测试goRouterTest(){// this.$router.push('/testpage');this.$router.push({ name: 'TestPage', params: { aaa: '111', bbb: '222' } });}
}
这样传参时,地址栏就会出现参数了,这样属性就不会丢失了。

然后,可以选择配合路由解耦来使用
修改路由配置为:
{// path: '/testPage', //这种方式不配置参数名,页面刷新会丢失参数path: '/testPage/:aaa/:bbb', //这样通过name和params进行路由传参时,刷新页面就不会丢失参数aaa和bbb了name: 'TestPage',props: true, //若个要解耦的 到组件中 props 中。component:() => import('@/views/TestPage/TestPage.vue')
}
要调整的组件生命 props:
<template><div class="TestPage">Name路由传参{{ $route.params }}</div>
</template>
<script>
export default {name: "TestPage",props: {//将路由中的参数aaa和bbb解耦到组件上的props上aaa: {type: String,},bbb: {type: String,},},mounted() {console.log("这是路由传的参数aaa",this.aaa,"这是路由传的参数bbb",this.bbb);},
};
</script>
<style scoped>
</style>最后的效果(刷新页面参数不会丢失):

😉 完美搞定!
当然也可以通过 path(或name) 和 query 的方式进行传参 this.$router.push({path: 路由路径,query: { 要传的参数 } }),但是这就不能进行props解耦了。
🙋♂️ 实现vue配置可选路由参数
假如下面是我们的某个路由:
{path: 'examPaperMultiPurpose/:action/:id', //多加 ? 代表这个参数是可选的。name: 'examPaperMultiPurpose',title: '考卷管理',notKeepAlive: true,props: true,component: () => import ('@/views/exam/examManage/examPaperMultiPurpose.vue'),
}当我们这样进行页面跳转时:
this.$router.push( { name: 'examPaperMultiPurpose', params: {action: 'add'} } );很显然我们在跳转时, 没有进行 id 参数 的 传递。我们在控制台也会看到这样的警告。

提醒我们缺少参数,id是一个没有定义的。
当我们有时候不是都想传递每个参数,我们可以把参数配置成可选的。配置方法为:在不想传递的参数后只要多加一个 ? 即可,如下代码:
//新增、编辑、查询考卷
{path: 'examPaperMultiPurpose/:action?/:id?', //多加 ? 代表这个参数是可选的。name: 'examPaperMultiPurpose',title: '考卷管理',notKeepAlive: true,props: true,component: () => import ('@/views/exam/examManage/examPaperMultiPurpose.vue'),
}这样,我们就把两个参数action 和 id 配置成可选的路由参数了,之后,当我们继续进行上面的方式进行传参时,就不会警告我们 缺少参数了。
🙋♂️ 参考资料
- 响应路由参数的变化
带参数的动态路由匹配 | Vue Router
- 路由组件传参
将 props 传递给路由组件 | Vue Router
- vue路由参数可选
vue路由可选参数,可有可无
- 路由跳转及传参方式汇总
详解Vue中实现路由跳转传参的4种方式

相关文章:

解决:vue通过params传参刷新页面参数丢失问题以及实现vue路由可选参数的解决办法
目录 🙋♂️ 实现params传参,刷新页面不丢参 🙋♂️ 实现vue配置可选路由参数 🙋♂️ 参考资料 解决vue 通过 name 和 params 进行页面传参时,刷新页面参数丢失问题以及vue路由实现可选参数 🙋♂…...

将postman接口导出的json转换为markdown
您可以使用 Postman 官方提供的工具或第三方工具将 Collection 文件转换为 Markdown 文件。 方式一 Postman 官方提供的工具是 Newman,它是一个命令行工具,可以帮助您运行和测试 Postman Collection,还可以将 Collection 转换为多种格式&am…...

教您一招解决找素材困难好的方法
创作视频内容时,找到合适的素材是至关重要的。然而,有时候寻找视频素材可能会变得困难。本文将分享一些实用的方法,帮助您轻松解决找视频素材困难的问题。 素材库和在线平台是寻找视频素材的首选方法。 利用专业的视频剪辑工具 在电脑上安…...

python_PyQt5开发验证K线视觉想法工具V1.2_批量验证
目录 运行情况: 编辑 结果json文件格式: 代码: 承接 【python_PyQt5开发验证K线视觉想法工具V1.1 _增加标记类型_线段】 博文 地址:python_PyQt5开发验证K线视觉想法工具V1.1 _增加标记类型_线段_程序猿与金融与科技的博客-…...
的排查思路)
应急响应-web后门(中间件)的排查思路
0x01 获取当前网络架构 语言,数据库,中间件,系统环境等 0x02 分析思路 1.利用时间节点筛选日志行为 2.利用已知的漏洞在日志进行特征搜索,快速定位到目标ip等信息 3.后门查杀,获取后门信息,进一步定位目…...
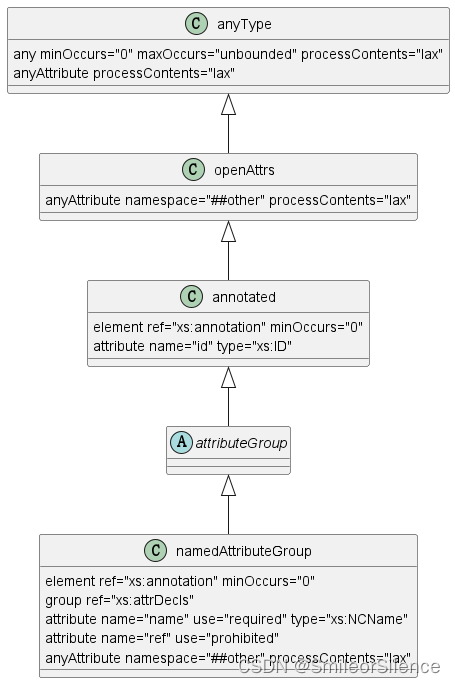
XML 学习笔记 7:XSD
本文章内容参考自: W3school XSD 教程 Extensible Markup Language (XML) 1.0 (Second Edition) XML Schema 2001 XML Schema Part 2: Datatypes Second Edition 文章目录 1、XSD 是什么2、XSD 内置数据类型 - built-in datatypes2.1、基本数据类型 19 种2.1.1、基本…...
)
neo4j图数据库基础操作命令(CQL语法)
天行健,君子以自强不息;地势坤,君子以厚德载物。 每个人都有惰性,但不断学习是好好生活的根本,共勉! 文章均为学习整理笔记,分享记录为主,如有错误请指正,共同学习进步。…...

vscode无法连接远程服务器的可能原因:远程服务器磁盘爆了
vscode输入密码后一直等待,无法进入远程服务器终端: 同时Remote-SSH输出包含以下内容 在日志中的以下几个部分: [17:15:05.529] > wget download failed 这表明VS Code尝试在远程服务器上下载VS Code服务器时失败了。> Cannot write…...
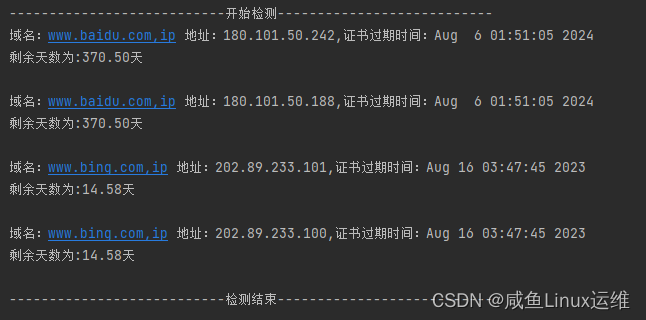
SSL 证书过期巡检脚本 (Python 版)
哈喽大家好,我是咸鱼 之前写了个 shell 版本的 SSL 证书过期巡检脚本 (文章:《SSL 证书过期巡检脚本》),后台反响还是很不错的 那么今天咸鱼给大家介绍一下 python 版本的 SSL 证书过期巡检脚本 (完整代码…...

从0到1自学网络安全(黑客)【附学习路线图+配套搭建资源】
前言 网络安全产业就像一个江湖,各色人等聚集。相对于欧美国家基础扎实(懂加密、会防护、能挖洞、擅工程)的众多名门正派,我国的人才更多的属于旁门左道(很多白帽子可能会不服气),因此在未来的…...

Michael.W基于Foundry精读Openzeppelin第20期——EnumerableMap.sol
0. 版本 [openzeppelin]:v4.8.3,[forge-std]:v1.5.6 0.1 EnumerableMap.sol Github: https://github.com/OpenZeppelin/openzeppelin-contracts/blob/v4.8.3/contracts/utils/structs/EnumerableMap.sol EnumerableMap库提供了Bytes32ToB…...

深入探索二叉树:应用、计算和遍历
当涉及到二叉树的计算问题时,我们可以进一步介绍如何计算叶子节点数、树的宽度和叶子的深度,并解释三种常见的二叉树遍历方式:先序遍历、中序遍历和后序遍历。 1. 计算叶子节点数 叶子节点是指没有子节点的节点,也就是树中的末端…...

关于 1 + 1 = 2 的证明
1 1 2 首先是皮亚诺的自然数公理 意大利数学家皮亚诺提出的关于自然数的 5 5 5 条公理如下(定义 S ( x ) S(x) S(x) 为自然数 x x x 的后继): 0 0 0 是自然数每一个自然数 n n n 都有一个自然数后继记为 S ( n ) S(n) S(n) 0 0 0 不是…...
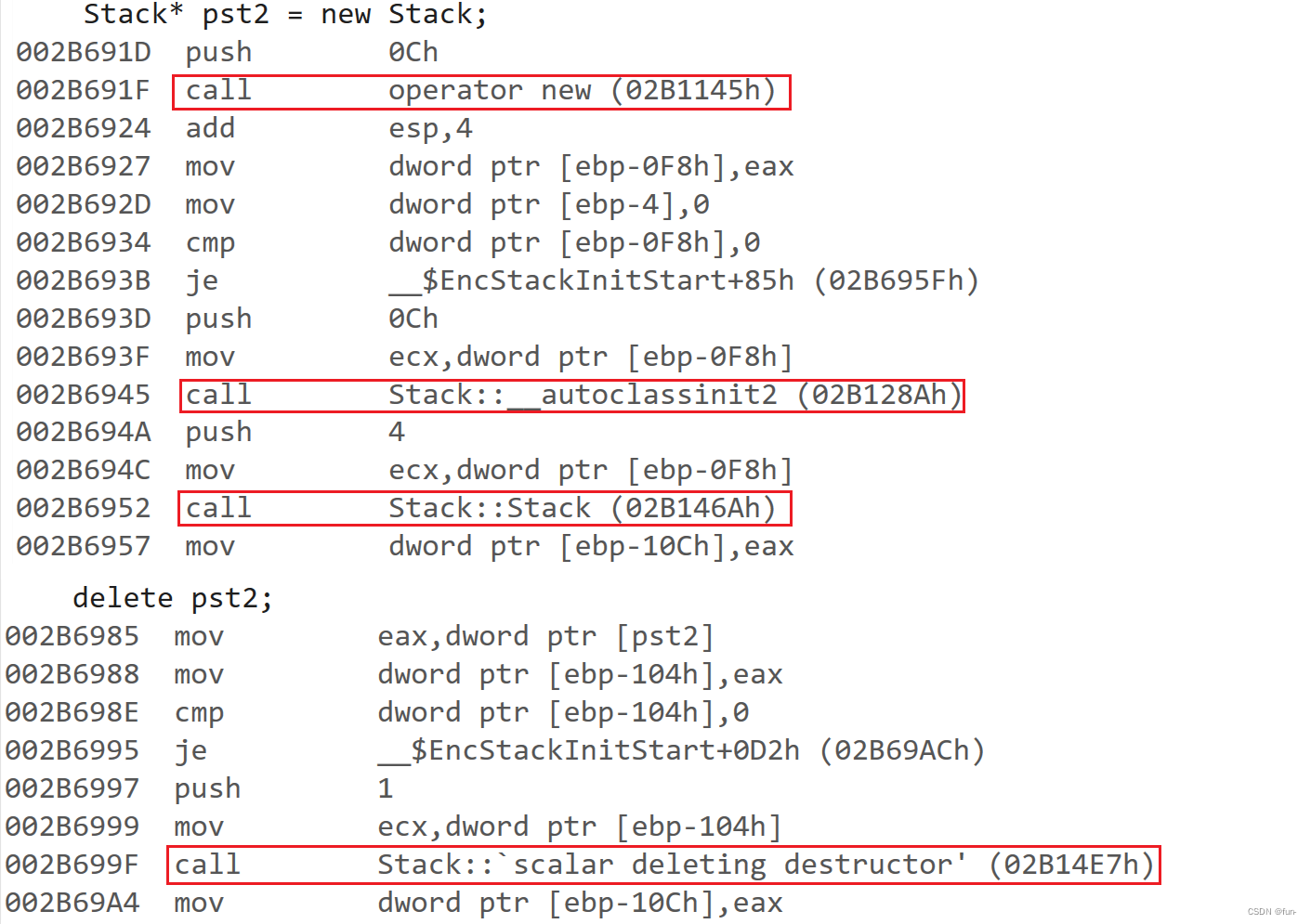
【C++】——内存管理
目录 回忆C语言内存管理C内存管理方式new deleteoperator new与operator delete函数new和delete的实现原理定位new表达式(placement-new)malloc/free和new/delete的区别 回忆C语言内存管理 void Test() {int* p1 (int*)malloc(sizeof(int));free(p1);int* p2 (int*)calloc(4…...

Jmeter录制HTTPS脚本
Jmeter录制HTTPS脚本 文章目录 添加“HTTP代理服务器”设置浏览器代理证书导入存在问题 添加“HTTP代理服务器” 设置浏览器代理 保持端口一致 证书导入 点击一下启动让jmeter自动生成证书,放在bin目录下: 打开jmeter的SSL管理器选择刚刚生成的证书&…...

Linux 的Centos 7 安装 启动 Google Chrome
我之所以在Centos上安装Chrome主要是为了让Web自动化测试工具可以启动Chrome,协助我做一些工作。 参考:centos7 google-chrome的安装与启动 - 简书 1.安装chrome逻辑 1. 下载安装包 2. 安装 3. 启动 》这就是在window上的逻辑,只是用命令行…...

DNS WEB HTTP
DNS与域名 网络是基于 TCP/IP 协议进行通信和连接的。 每一台主机都有唯一的标识,用于区别在网络上成千上万个用户和计算机。即固定的IP地址(32位二进制数转换成为十进制数——点分十进制)。每一个与网络相连接的计算机和服务器都被指派一个…...
微信小程序animation动画,微信小程序animation动画无限循环播放
需求是酱紫的: 页面顶部的喇叭通知,内容不固定,宽度不固定,就是做走马灯(轮播)效果,从左到右的走马灯(轮播),每播放一遍暂停 1500ms ~ 2000ms 刚…...

node.js
什么是Node.js Node.js 是一个免费的、开源的、跨平台的 JavaScript 运行时环境,使开发者可以搭建服务器端的JavaScript应用程序 概念: 使用Node.js编写后端程序 // 支持前端工程化 后端程序:提供接口和数据 ,网页资源 前端工程化:对代码压缩&…...
【微信小程序创作之路】- 小程序远程数据请求、获取个人信息
【微信小程序创作之路】- 小程序远程数据请求、获取个人信息 第七章 小程序远程数据请求、获取个人信息 文章目录 【微信小程序创作之路】- 小程序远程数据请求、获取个人信息前言一、远程数据请求1.本地环境2.正式域名 二、获取用户个人信息1.展示当前用户的身份信息2.获取用…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...
