243. 一个简单的整数问题2(树状数组)

输入样例:
10 5
1 2 3 4 5 6 7 8 9 10
Q 4 4
Q 1 10
Q 2 4
C 3 6 3
Q 2 4
输出样例:
4
55
9
15解析:
一般树状数组都是单点修改、区间查询或者单点查询、区间修改。这道题都是区间操作。
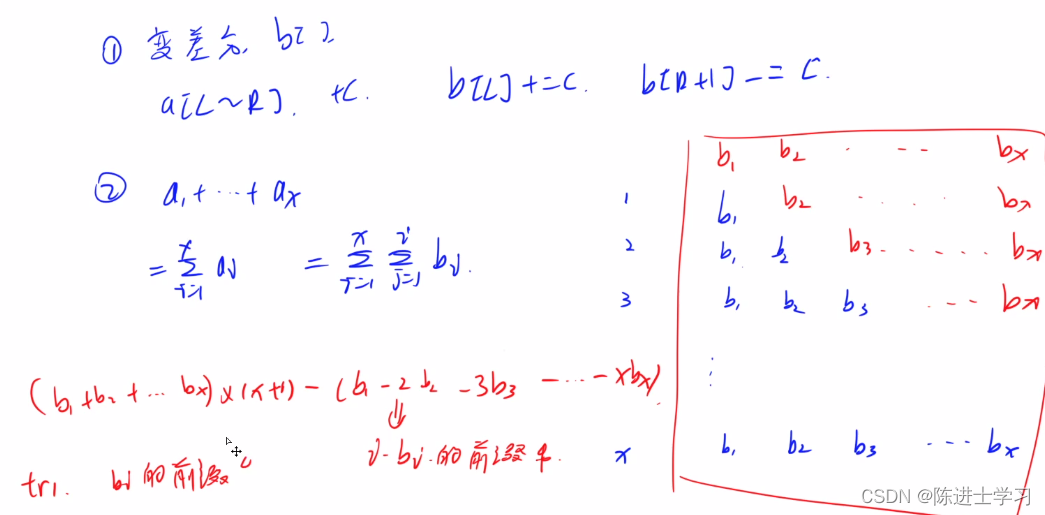
1. 区间修改用数组数组维护差分数组
2. 区间查询,需要log计算两个端点的前缀和。上图右侧,可以得出,计算前缀和需要维护差分序列和 i*b[ i ] 的差分序列。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+5;
ll n,m,a[N],b[N],tr1[N],tr2[N];
int lowbit(int x){return x&-x;
}
void add1(int x,ll k){for(int i=x;i<=n;i+=lowbit(i)) tr1[i]+=k;
}
void add2(int x,ll k){for(int i=x;i<=n;i+=lowbit(i)) tr2[i]+=k;
}
ll sum(int x){ll ans=0;for(int i=x;i;i-=lowbit(i)) ans+=tr1[i];ans*=x+1;for(int i=x;i;i-=lowbit(i)) ans-=tr2[i];return ans;
}
int main(){scanf("%lld%lld",&n,&m);for(int i=1;i<=n;i++){scanf("%lld",&a[i]);b[i]=a[i]-a[i-1];add1(i,b[i]);add2(i,i*b[i]);}while(m--){char op;cin>>op;if(op=='C'){int l,r,d;scanf("%lld%lld%lld",&l,&r,&d);add1(l,d);add1(r+1,-d);add2(l,d*l);add2(r+1,-d*(r+1));}else{int x,y;scanf("%lld%lld",&x,&y);printf("%lld\n",sum(y)-sum(x-1));}}return 0;
}相关文章:
243. 一个简单的整数问题2(树状数组)
输入样例: 10 5 1 2 3 4 5 6 7 8 9 10 Q 4 4 Q 1 10 Q 2 4 C 3 6 3 Q 2 4输出样例: 4 55 9 15 解析: 一般树状数组都是单点修改、区间查询或者单点查询、区间修改。这道题都是区间操作。 1. 区间修改用数组数组维护差分数组 2. 区间查询&am…...
C#利用自定义特性以及反射,来提大型项目的开发的效率
在大型项目的开发过程中,需要多人协同工作,来加速项目完成进度。 比如一个软件有100个form,分给100个人来写,每个人完成自己的Form.cs的编写之后,要在Mainform调用自己写的Form。 如果按照正常的Form form1 new For…...

【传统视觉】C#创建、封装、调用类库
任务 因为实现代码相对简单,然后又没有使用Opencv,所以就直接用C#实现,C#调用。 1.创建类库 1.1新建一个类库 vs2015 > 文件 > 新建 > 项目 using System; using System.Collections.Generic; using System.Linq;namespace Yo…...

AutoMapper反向映射
#region 用来验证反向映射public class MemberSource{public string Name { get; set; }public MemberInnerSource MemberInnerSource { get; set; }public MemberOtherInnerSource MemberOtherInnerSource { get; set; }}public class MemberInnerSource{public string Name {…...

华为Mate30报名鸿蒙 HarmonyOS 4.0.0.108 系统更新
华为 Mate 30 系列于 2019 年 11 月 1 日上市,包括 Mate 30 4G / 5G、Mate 30 Pro 4G / 5G、保时捷设计版 Mate30 共五款机型。华为 Mate 30 系列 5G 版搭载麒麟 990 5G 处理器,同时支持 SA 及 NSA 5G 双模,适配三大运营商的 5G / 4G / 3G / …...
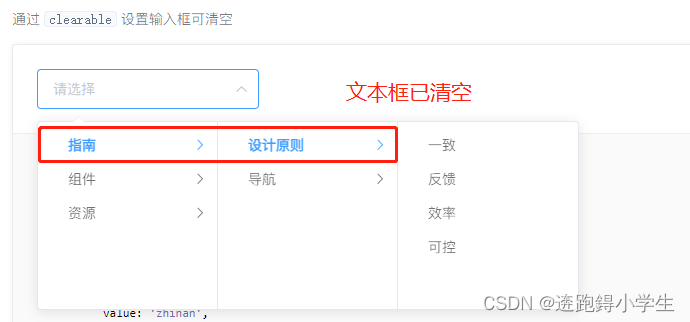
elementui Cascader 级联选择使用心得
相信大家对于elementui并不陌生,作为适配Vue的优秀UI框架之一,一直被所有的开发者痛并快乐着。今天要记录的就是里边的主角之一Cascader。 首先先介绍一下Cascader ---> 当一个数据集合有清晰的层级结构时,可通过级联选择器逐级查看并选择…...

【ChatGPT 指令大全】怎么利用ChatGPT写报告
目录 选定切入角度 报告开头 大纲生成 草稿撰写 研究报告 提出反对观点 报告总结 研究来源 总结 随着人工智能技术的快速发展,自然语言处理技术在各个领域的应用越来越广泛。其中,ChatGPT作为目前最先进的自然语言处理模型之一,其强…...
【枚举,构造】CF1582 C D
Problem - C - Codeforces 题意: 思路: 思路很简单,只删除一种,直接枚举删除的是哪一种即可 但是回文子序列的判定我vp的时候写的很答辩,也不知道为什么当时要从中间往两边扫,纯纯自找麻烦 然后就越改越…...

POJ 3169 Layout BellmanFord Dijkstra
一、心路历程 这一个题目写了三天,可以说是非常挣扎了,明明是例题,但是就是倔强着不去看书上的题解,WA了7次,TLE了4次。 写了不知道多少条测试用例,一遍一遍的过,一点一点的调试。 最后终于找到…...

数据库管理员知识图谱
初入职场的程序猿,需要为自己做好职业规划,在职场的赛道上,需要保持学习,并不断点亮自己的技能树。 成为一名DBA需要掌握什么技能呢,先让Chat-GPT为我们回答一下: 数据库管理系统 (DBMS)知识ÿ…...

中兴服务器支持百度“文心一言”,助力AI产业发展
前段时间,中兴和百度正式对外宣布中兴服务器将会支持百度“文心一言”,为其提供更加强劲的算力支撑,从而加速“文心一言”的完事升级与更新迭代,助力AI产业化应用和生态的繁荣发展。 “文心一言”是百度基于文心大模型技术推出…...

STM 如何通过网络 time.windows.com获取时间
STM 如何通过网络 time.windows.com获取时间 在STM32中,你可以使用STM32Cube HAL库提供的网络套接字API来通过网络获取时间。以下是一个示例代码,演示如何通过time.windows.com获取时间: #include "stm32xxxx.h" #include "lwip/sockets.h" #include …...
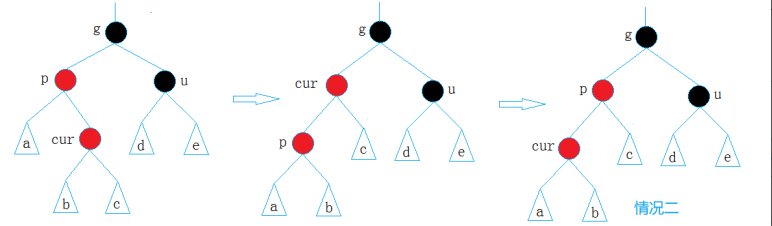
数据结构——红黑树
文章目录 一.红黑树的定义二.红黑树的插入1.红黑树节点的定义2.红黑树的插入操作3.总结: 三.红黑树与AVL树的比较四.检验手写的红黑树五.源码 一.红黑树的定义 红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色ÿ…...

【C++】数据结构与算法:常用排序算法
😏★,:.☆( ̄▽ ̄)/$:.★ 😏 这篇文章主要介绍常用排序算法。 学其所用,用其所学。——梁启超 欢迎来到我的博客,一起学习,共同进步。 喜欢的朋友可以关注一下,下次更新不迷路…...

【C++】Bullet3代码存档
之前试了一下Bullet3物理引擎,但在linux上编译失败,于是放弃了。令我不满的还有另外一个原因,下载的发行包竟然有500M。C的Bullet3代码根本用不了,大部分教程实际都是用的老版本。而且此项目还整了python版本,各种蹭人…...

弘扬“两弹一星”精神,勇攀科学技术高峰——道本科技商业大学党日活动圆满落幕
2023年8月2日,道本科技与商业大学携手举办了一场主题为“弘扬‘两弹一星’精神,勇攀科学技术高峰”的党日活动。本次活动旨在了解党领导下的中国核工业发展历程,传承和弘扬“两弹一星”精神,同时展示道本科技创新产品,…...

Java中创建对象的几种方式
背景 面试的时候有些面试官喜欢问这些, 这里简单记录一下. 常见方式 方式1: new XXXX(); 使用new关键字:这是最常见的创建对象的方式,使用new关键字后面跟上类名和参数列表(如果有),可以调用类的构造方法来创建对象…...

Python(三)
诚信像一面镜子,一旦打破,你的人格就会出现裂痕。 存在短路的情景 谢谢观看 Python(三)...

android 如何分析应用的内存(十五)——Visual Studio Code 调试Android应用
android 如何分析应用的内存(十五)——Visual Studio Code 调试Android 应用 在上一篇文章介绍了jdb调试java应用 接下来介绍用UI界面调试java应用,达到同jdb一样的效果。 同样的UI界面有很多选择,如Eclipse,Android …...

宁波银行最新内推码 MK4913
宁波银行最新内推码 MK4913 内推码: MK4913 内推二维码 : 网申路径: 网页端:登录宁波银行招聘官网: https://zhaopin.nbcb.com.cn 选择【校园招聘】-【招聘岗位】手机端:关注【宁波银行招聘】公众号&a…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...

Git 命令全流程总结
以下是从初始化到版本控制、查看记录、撤回操作的 Git 命令全流程总结,按操作场景分类整理: 一、初始化与基础操作 操作命令初始化仓库git init添加所有文件到暂存区git add .提交到本地仓库git commit -m "提交描述"首次提交需配置身份git c…...

2025 后端自学UNIAPP【项目实战:旅游项目】7、景点详情页面【完结】
1、获取景点详情的请求【my_api.js】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http(/login/getWXSessionKey, {code,avatar}); };//…...

MyBatis-Plus 常用条件构造方法
1.常用条件方法 方法 说明eq等于 ne不等于 <>gt大于 >ge大于等于 >lt小于 <le小于等于 <betweenBETWEEN 值1 AND 值2notBetweenNOT BETWEEN 值1 AND 值2likeLIKE %值%notLikeNOT LIKE %值%likeLeftLIKE %值likeRightLIKE 值%isNull字段 IS NULLisNotNull字段…...
