数据结构-二叉树
数据结构-二叉树
- 二叉树的概念
- 二叉树的遍历分类
- 建立二叉树,并遍历
- 二叉树的最小单元
- 二叉树的最小单元初始化
- 初始化二叉树
- 前序遍历的实现
- 中序遍历的实现
- 后序遍历的实现
- 计算节点的个数
- 计算树的深度
- 求第k层的个数
- 查找二叉树的元素
- 分层遍历
- 全部代码如下
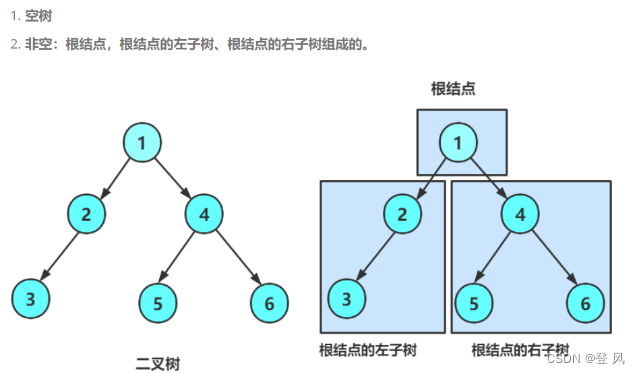
二叉树的概念
二叉树的遍历分类
有前序遍历,中序遍历,后序遍历和层序遍历
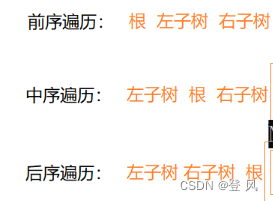
规则:
1.遇到根可以直接访问根
2.遇到左子树,右子树,不可以直接访问,要将其看作一颗新的二叉树,按遍历规则,再次循环,直至左子树或右子树为空,则可访问空。
前序遍历
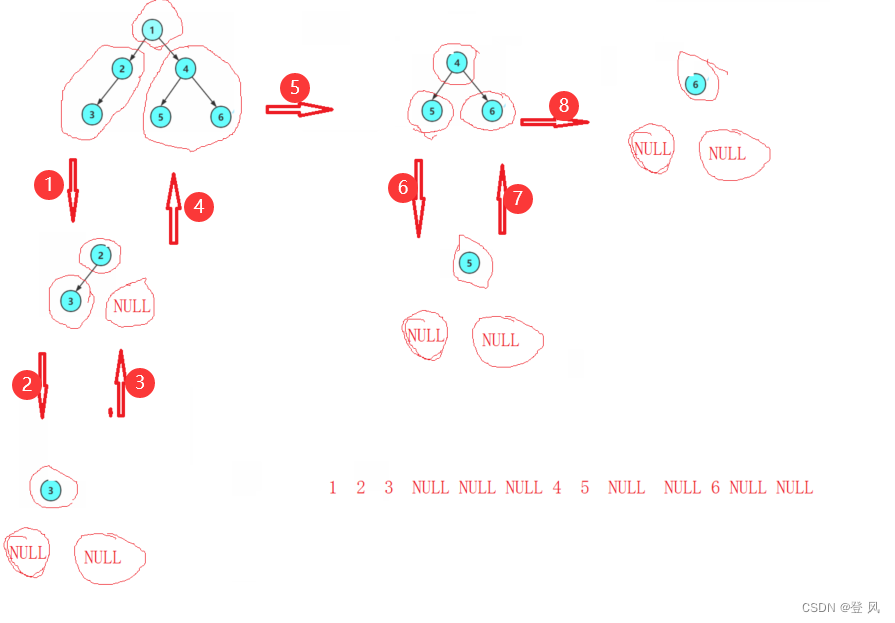
中序遍历和后序遍历

三者访问根的时机不同
层序遍历:一层一层的进行
1 2 4 3 5 6
建立二叉树,并遍历
二叉树的最小单元
根,左子树和右子树
typedef int BTDataType;typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;
二叉树的最小单元初始化
BTNode* BuyNode(BTDataType x)
{BTNode* node=(BTNode*)malloc(sizeof(BTNode));if (node==NULL){perror("malloc fail");return NULL;}node->data = x;node->left = NULL;node->right = NULL;return node;
}
初始化二叉树
BTNode* CreatTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right=node6;return node1;
}
前序遍历的实现
函数的回归条件为root为空,或者函数正常结束
按照顺序依次为:根,左子树,右子树
void PreOrder(BTNode* root)
{if (root==NULL){printf("NULL ");return;}//root,left,rightprintf("%d ",root->data);PreOrder(root->left);PreOrder(root->right);
}
递归调用展开图
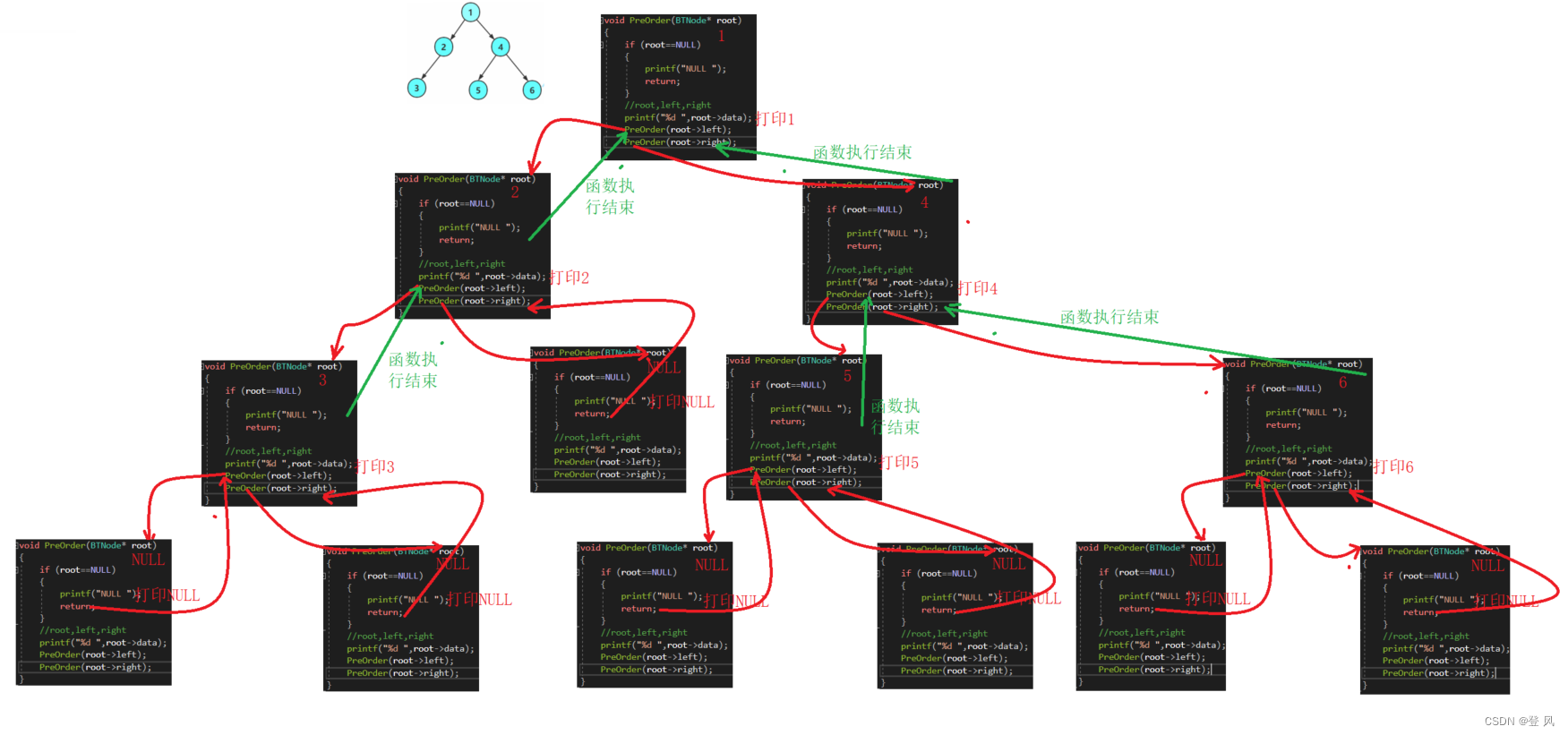
结果如下:

中序遍历的实现
函数的回归条件为root为空,或者函数正常结束
按照顺序依次为:左子树,根,右子树
void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}
后序遍历的实现
函数的回归条件为root为空,或者函数正常结束
按照顺序依次为:左子树,右子树,根
void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);
}
计算节点的个数
利用分治法求节点的个数,只有节点存在时,才会+1,并返回下层的统计个数
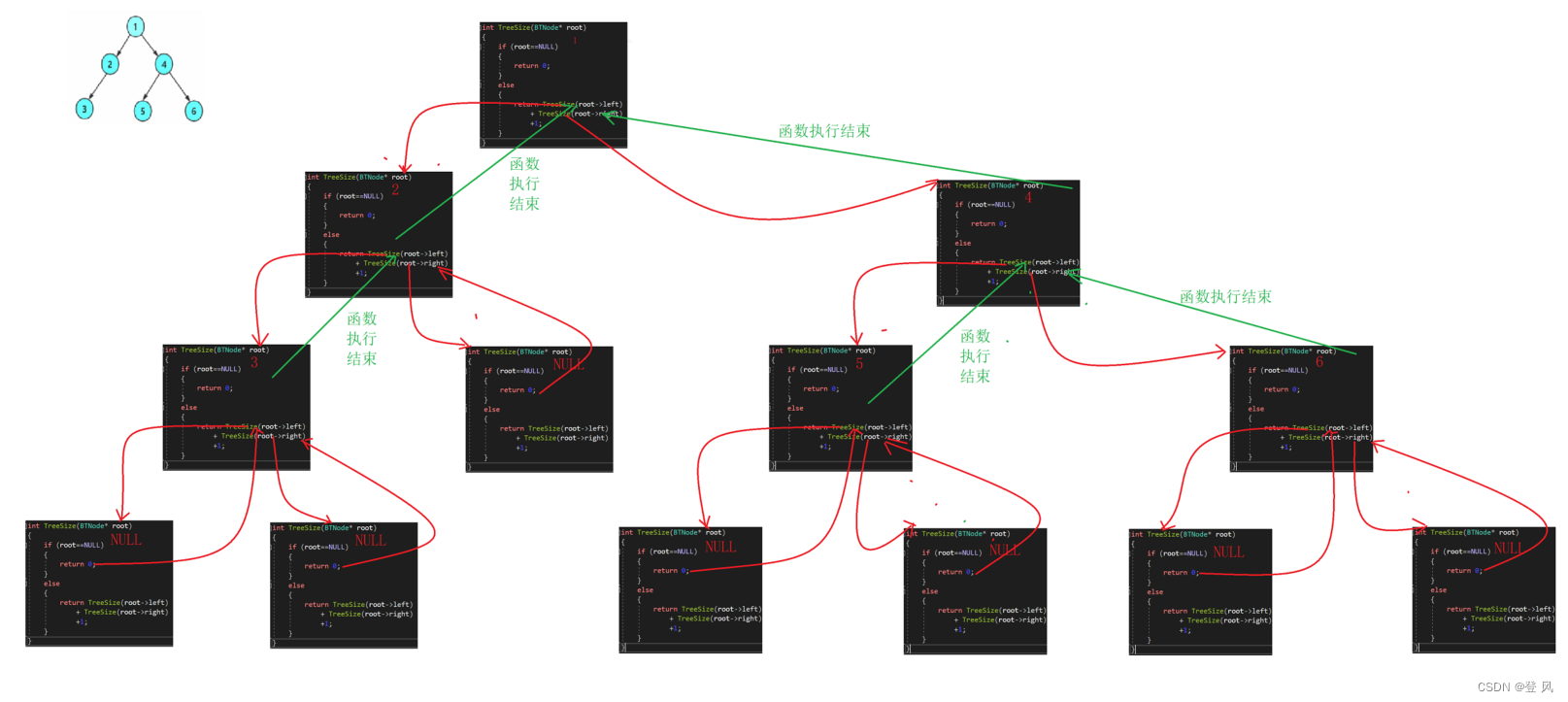
int TreeSize(BTNode* root)
{if (root==NULL){return 0;}else{return TreeSize(root->left) + TreeSize(root->right)+1;}
}
执行结果如下:

计算树的深度
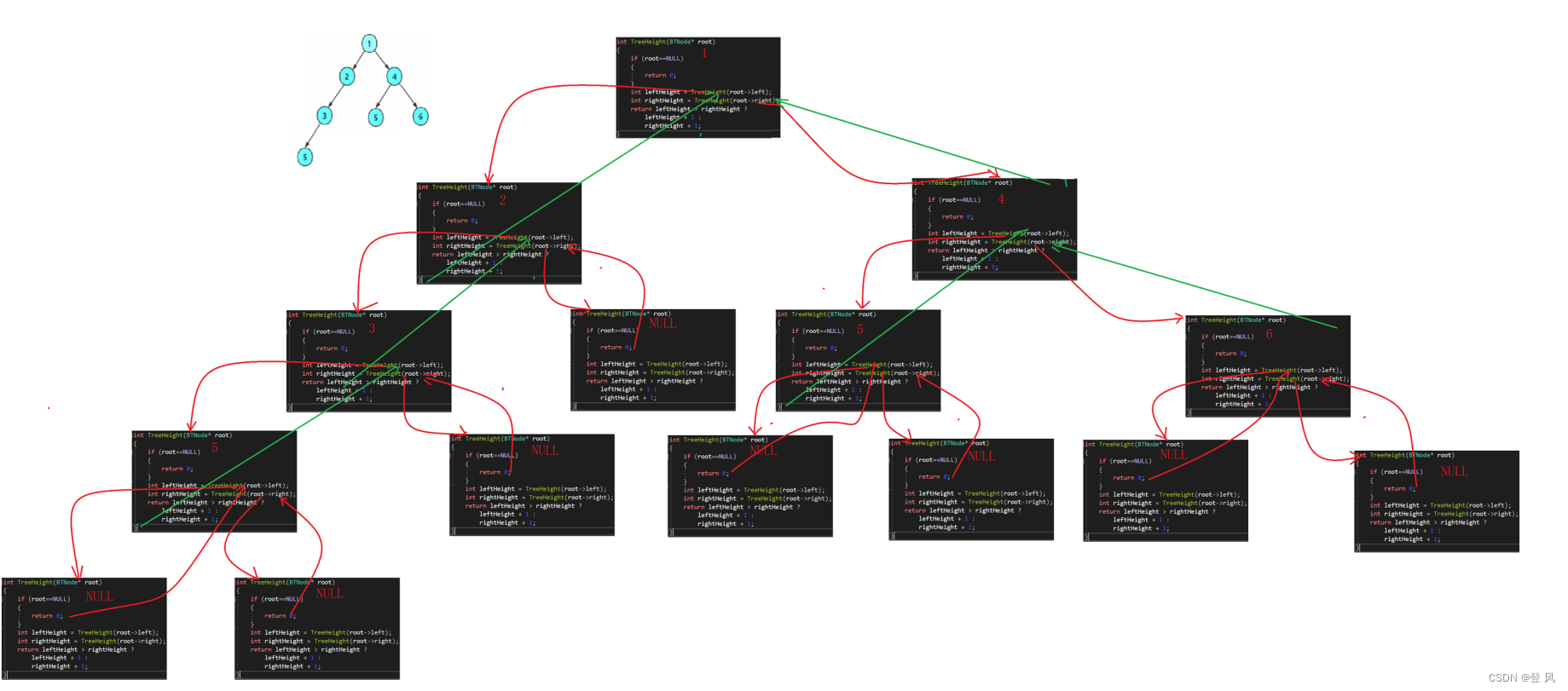
int TreeHeight(BTNode* root)
{if (root==NULL){return 0;}int leftHeight = TreeHeight(root->left);int rightHeight = TreeHeight(root->right);return leftHeight > rightHeight ?leftHeight + 1 :rightHeight + 1;
}
代码执行结果如下:

求第k层的个数

int TreeLevel(BTNode* root,int k)
{if (root==NULL){return 0;}if (k==1){return 1;}return TreeLevel(root->left, k - 1) + TreeLevel(root->right, k - 1);
}
运行结果如下:

查找二叉树的元素
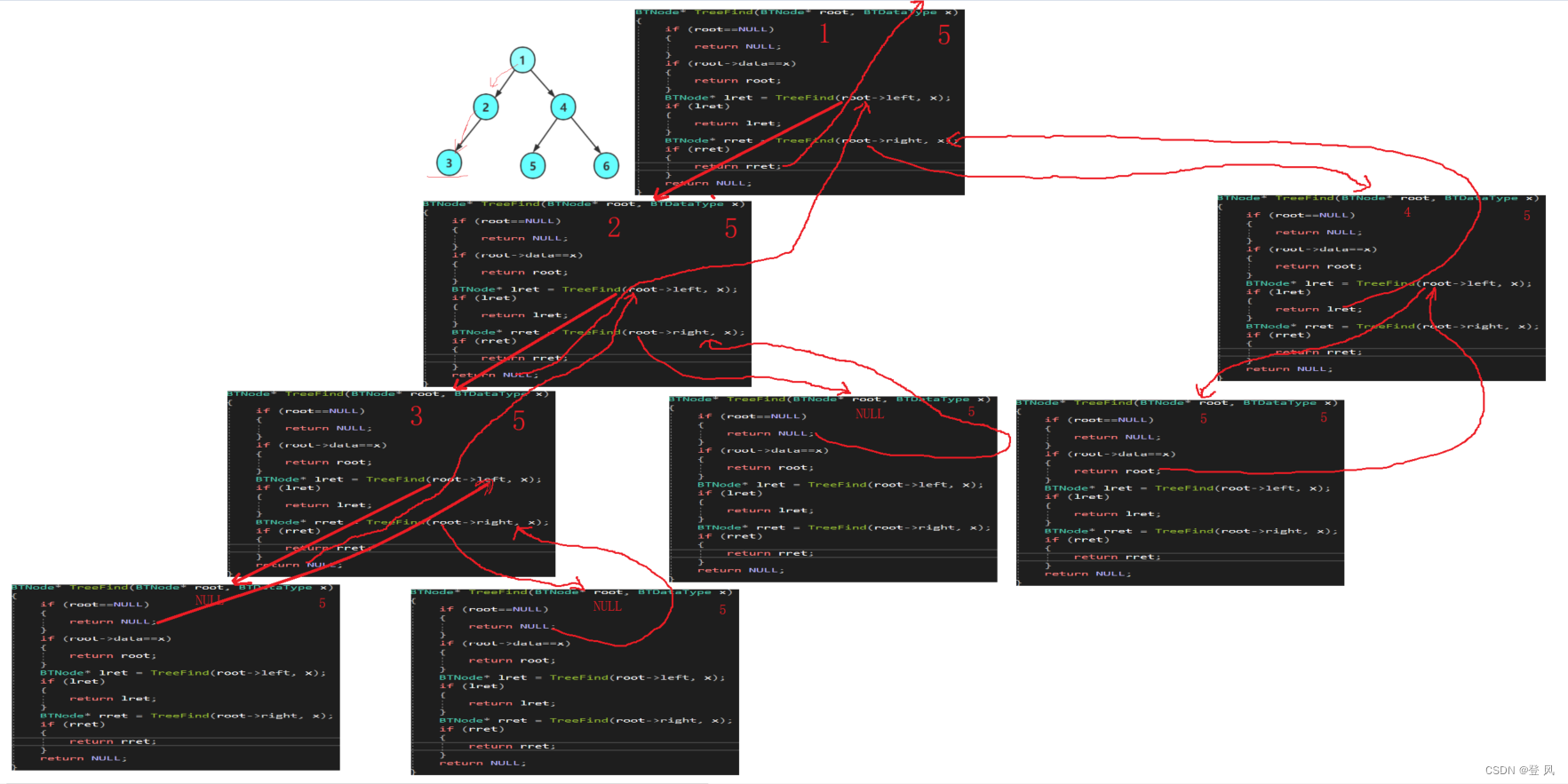
BTNode* TreeFind(BTNode* root, BTDataType x)
{if (root==NULL){return NULL;}if (root->data==x){return root;}BTNode* lret = TreeFind(root->left, x);if (lret){return lret;}BTNode* rret = TreeFind(root->right, x);if (rret){return rret;}return NULL;
}
结果如下:
分层遍历
利用队列,先将根push,进入循环,可pop,再将层子节点push,依次循环。安照队列先进先出的原则,可实现分层打印
void LevelOrder(BTNode* root)
{Quene q;QueueInit(&q);if (root){QueuePush(&q,root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);printf("%d ",front->data);if (front->left){QueuePush(&q, front->left);}if (front->right){QueuePush(&q, front->right);}}QueueDestroy(&q);
}
结果如下:

判断是否为完全二叉树
bool TreeComplete(BTNode* root)
{Quene q;QueueInit(&q);if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front==NULL){break;}else{QueuePush(&q, front->left);QueuePush(&q, front->right);}}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front){QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;
}
全部代码如下
test.c
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdlib.h>
#include "Queue.h"typedef int BTDataType;typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;BTNode* BuyNode(BTDataType x)
{BTNode* node=(BTNode*)malloc(sizeof(BTNode));if (node==NULL){perror("malloc fail");return NULL;}node->data = x;node->left = NULL;node->right = NULL;return node;
}BTNode* CreatTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);//BTNode* node6 = BuyNode(6);//node1->left = node2;//node1->right = node4;//node2->left = node3;//node4->left = node5;//node4->right=node6;node1->left = node2;node1->right = node3;node2->left = node4;//node4->left = node5;node3->right = node5;return node1;
}void PreOrder(BTNode* root)
{if (root==NULL){printf("NULL ");return;}//root,left,rightprintf("%d ",root->data);PreOrder(root->left);PreOrder(root->right);
}void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);
}//分治法求节点的个数
int TreeSize(BTNode* root)
{if (root==NULL){return 0;}else{return TreeSize(root->left) + TreeSize(root->right)+1;}
}int TreeHeight(BTNode* root)
{if (root==NULL){return 0;}int leftHeight = TreeHeight(root->left);int rightHeight = TreeHeight(root->right);return leftHeight > rightHeight ?leftHeight + 1 :rightHeight + 1;
}int TreeLevel(BTNode* root,int k)
{if (root==NULL){return 0;}if (k==1){return 1;}return TreeLevel(root->left, k - 1) + TreeLevel(root->right, k - 1);
}//查找元素
BTNode* TreeFind(BTNode* root, BTDataType x)
{if (root==NULL){return NULL;}if (root->data==x){return root;}BTNode* lret = TreeFind(root->left, x);if (lret){return lret;}BTNode* rret = TreeFind(root->right, x);if (rret){return rret;}return NULL;
}//分层遍历
void LevelOrder(BTNode* root)
{Quene q;QueueInit(&q);if (root){QueuePush(&q,root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);printf("%d ",front->data);if (front->left){QueuePush(&q, front->left);}if (front->right){QueuePush(&q, front->right);}}QueueDestroy(&q);
}//判断是不是完全二叉树
bool TreeComplete(BTNode* root)
{Quene q;QueueInit(&q);if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front==NULL){break;}else{QueuePush(&q, front->left);QueuePush(&q, front->right);}}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front){QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;
}
int main()
{BTNode* root = CreatTree();PreOrder(root);printf("\n");InOrder(root);printf("\n");PostOrder(root);printf("\n");printf("%d",TreeSize(root));printf("\n");printf("%d ", TreeHeight(root));printf("\n");printf("%d ", TreeLevel(root,3));printf("\n");printf("%p ", TreeFind(root, 5));printf("\n");printf("%p ", TreeFind(root, 60));printf("\n");LevelOrder(root);printf("TreeComplete: %d", TreeComplete(root));//二维数组return 0;
}
Queue.c
#define _CRT_SECURE_NO_WARNINGS 1
#include "Queue.h"void QueueInit(Quene* pq)
{assert(pq);pq->head = pq->tail = NULL;pq->size = 0;
}void QueueDestroy(Quene* pq)
{assert(pq);QNode* cur = pq->head;while(cur){QNode* next = cur->next;free(cur);cur = next;}pq->head = pq->tail = NULL;pq->size = 0;
}void QueuePush(Quene* pq, QDataType x)
{assert(pq);QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode==NULL){perror("malloc fail");return;}newnode->next = NULL;newnode->data = x;//需要判断队列中是否有元素if (pq->head==NULL){pq->head = pq->tail = newnode;}else{pq->tail->next = newnode;pq->tail = newnode;}pq->size++;
}void QueuePop(Quene* pq)
{assert(pq);//确保有队列assert(pq->head != NULL);//确保队列不为空if (pq->head->next==NULL){free(pq->head);pq->head = pq->tail = NULL;}else{QNode* next = pq->head->next;free(pq->head);pq->head = next;}pq->size--;
}int QueueSize(Quene* pq)
{assert(pq);return pq->size;
}bool QueueEmpty(Quene* pq)
{assert(pq);return pq->size==0;
}QDataType QueueFront(Quene* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->head->data;
}QDataType QueueBack(Quene* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->tail->data;
}
Queue.h
#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <assert.h>typedef struct BinaryTreeNode* QDataType;//单个节点
typedef struct QueneNode
{struct QueneNode* next;QDataType data;
}QNode;//整个队列
typedef struct Quene
{QNode* head;QNode* tail;int size;
}Quene;//初始化
void QueueInit(Quene* pq);
//销毁
void QueueDestroy(Quene* pq);//入队
void QueuePush(Quene* pq, QDataType x);
//出队
void QueuePop(Quene* pq);//计算队列中元素的个数
int QueueSize(Quene* pq);
//判断队列是否为空
bool QueueEmpty(Quene* pq);//队列中的队头元素
QDataType QueueFront(Quene* pq);
//队列中的队尾元素
QDataType QueueBack(Quene* pq);
相关文章:

数据结构-二叉树
数据结构-二叉树 二叉树的概念二叉树的遍历分类 建立二叉树,并遍历二叉树的最小单元二叉树的最小单元初始化初始化二叉树前序遍历的实现中序遍历的实现后序遍历的实现计算节点的个数计算树的深度求第k层的个数查找二叉树的元素分层遍历 全部代码如下 二叉树的概念 二…...

Open3D 进阶(4)高斯混合点云聚类
目录 一、算法原理1、原理概述2、实现流程3、参考文献二、代码实现三、结果展示四、测试数据本文由CSDN点云侠原创,原文链接。爬虫网站自重。 一、算法原理 1、原理概述 高斯混合聚类(GMM)算法假设数据点是由一个或多个高斯分布生成的,并通过最大似然估计的方法来估计每个簇…...

计算机组成和IO
文章目录 计组和Epoll:计算机组成原理:网络数据接收的流程:内核如何管理socket以及状态的更新select系统调用的复杂度epoll的et和lt模式及java的选择 国内访问chatai就可以 https://aiweb.douguguo.com/?typeadd计组和Epoll: 计…...
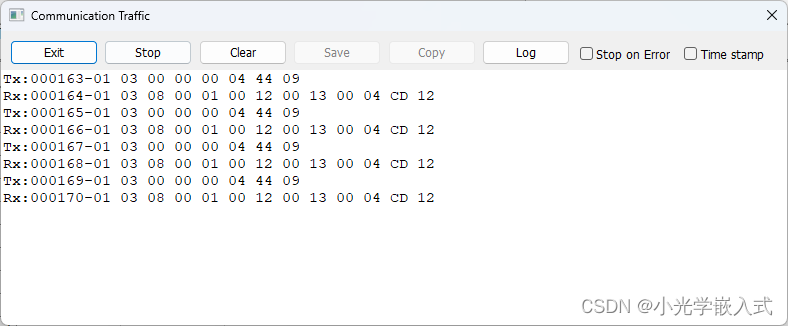
STM32CUBUMX配置RS485 modbus STM32(从机)亲测可用
———————————————————————————————————— ⏩ 大家好哇!我是小光,嵌入式爱好者,一个想要成为系统架构师的大三学生。 ⏩最近在开发一个STM32H723ZGT6的板子,使用STM32CUBEMX做了很多驱动&#x…...

系统设计类题目汇总
1 设计一个系统统计当前时刻北京用户在线人数 【Redis】位图以及位图的使用场景(统计在线人数和用户在线状态) 1.1 方案一: 在用户登录时,使用 Redis SET 将用户 ID 添加到一个特定的键(例如 “online:beijing”)。用户退出时&…...

css滚动条样式指南
css滚动条样式指南 滚动条是网页设计中经常被忽视的元素。虽然它看起来像是一个小细节,但它在网站导航中起着至关重要的作用。默认的滚动条可能看起来不合适,有损整体美观。本文将介绍如何使用 CSS 自定义滚动条。 在 Chrome、Edge 和 Safari 中设置滚…...
)
vue子组件修改父组件传递的变量(自定义日期时间组件,时间间隔为15分钟或者一个小时)
vue子组件修改父组件传递的变量 子组件不能直接修改父组件变量的值,但是可以通过调用父组件的方法来修改。 实现步骤 在父组件声明变量 export default {data() {return {startTime:"",......},......} }在父组件使用子组件并传递数据,修改…...

【PyTorch】nn.Conv2d函数详解
nn.Conv2d 是 PyTorch 中的一个卷积层,用于实现二维卷积操作 torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride1, padding0, dilation1, groups1, biasTrue, padding_modezeros, deviceNone, dtypeNone )参数解释 in_channels:输入的通…...

数智保险 创新未来 | GBASE南大通用亮相中国保险科技应用高峰论坛
本届峰会以“数智保险 创新未来”为主题,GBASE南大通用携新一代创新数据库产品及金融信创解决方案精彩亮相,与国内八百多位保险公司高管和众多保险科技公司技术专家,就保险领域数字化的创新应用及生态建设、新一代技术突破及发展机遇、前沿科…...

分布式天梯图算法在 Redis 图数据库中的应用
分布式天梯图算法在 Redis 图数据库中的应用 一、简介1 天梯图算法2 天梯图算法在Redis的应用 二、Redis分布式天梯图算法设计与优化1 基于天梯图的分布式算法设计2 多节点扩展与负载均衡优化3 数据存储方案与压缩策略 三、技术实现3.1 系统架构设计3.2 技术选型3.3 关键实现细…...
观察者模式——对象间的联动
1、简介 1.1、概述 在软件系统中,有些对象之间也存在类似交通信号灯和汽车之间的关系。一个对象的状态或行为的变化将导致其他对象的状态或行为也发生改变,它们之间将产生联动,正所谓“触一而牵百发”。为了更好地描述对象之间存在的这种一…...

【雕爷学编程】Arduino动手做(189)---特别苗条,使用微波传感器控制的纤细小车
装修屋子,找了一段墙面布线槽,外槽宽度只有23毫米,截取一段长为24厘米,尝试做个苗条小车 先在线槽上安装了二只N20小电机 装上二个快餐盒盖做轮子 测试一下使用3.7V锂电池的动力系统(视频) https://v.youk…...

机器学习基础算法及其实现
线性回归 知识点: 1. 线性回归模型可以使用不同的目标函数,最常用的是最小二乘法、最小绝对值法和最大似然法。 2. 在最小二乘法中,目标是最小化实际值与预测值之间的误差平方和,这可以通过求导数等方法来求解。 3. 在最小绝对值…...

docker安装MinIO
简介 Minio 是一个面向对象的简单高性能存储服务。使用 Go 语言编写,性能高、具有跨平台性。 Minio 官网为:https://min.io ,有一个中文站点,单内容更新不是很及时,建议从原始官网学习。 本文采用 Docker 安装&…...
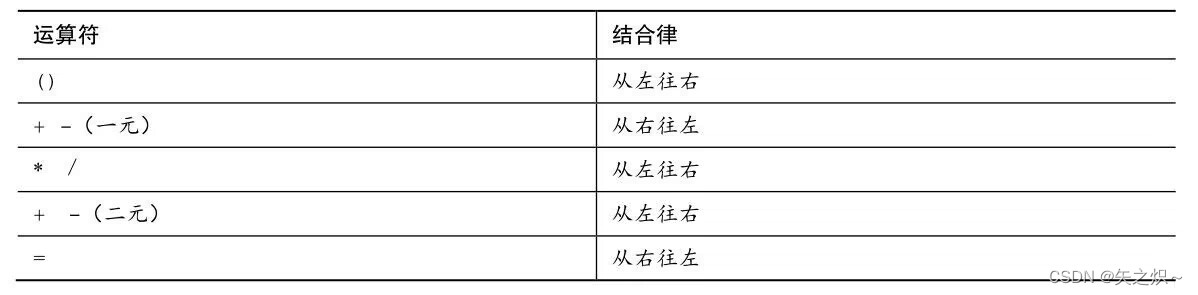
第5章 运算符、表达式和语句
本章介绍以下内容: 关键字:while、typedef 运算符:、-、*、/、%、、--、(类型名) C语言的各种运算符,包括用于普通数学运算的运算符 运算符优先级以及语句、表达式的含义 while循环 复合语句、自动类型转换和强制类型转换 如何编写…...

24考研数据结构-图的存储结构邻接矩阵
目录 6.3 储存结构(邻接表表示法)1. 储存方式2. 结构3. 图的邻接表存储表示(算法)4. 结论5. 邻接矩阵和邻接表的对比邻接矩阵优点:缺点: 邻接表优点:缺点: 邻接矩阵与邻接表的关系 6…...
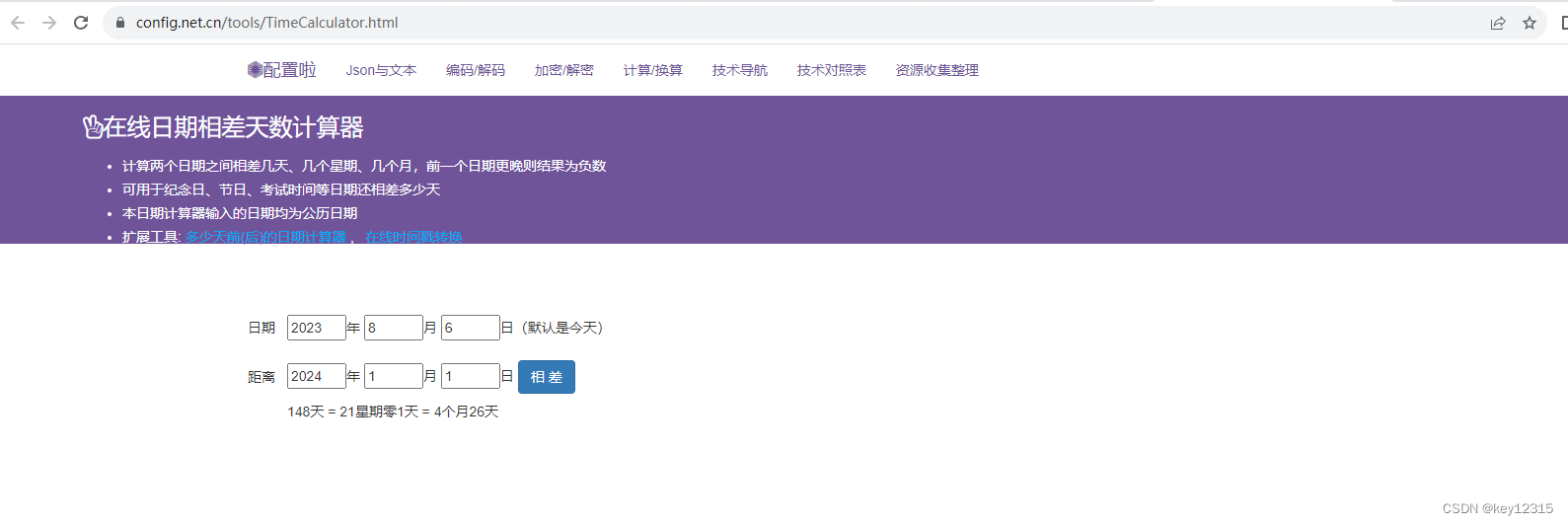
在线推算两个日期相差天数的计算器
具体请前往:在线推算两个日期相差天数的计算器...
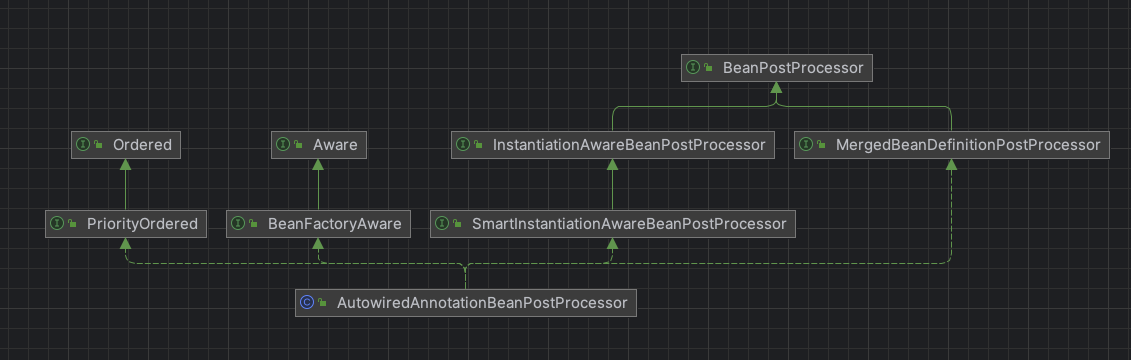
Spring源码解析(七):bean后置处理器AutowiredAnnotationBeanPostProcessor
Spring源码系列文章 Spring源码解析(一):环境搭建 Spring源码解析(二):bean容器的创建、默认后置处理器、扫描包路径bean Spring源码解析(三):bean容器的刷新 Spring源码解析(四):单例bean的创建流程 Spring源码解析(五)&…...

【C#学习笔记】引用类型(1)
文章目录 引用类型class匿名类 记录引用相等和值相等record声明 接口delegate 委托合并委托/多路广播委托 引用类型 引用类型的变量存储对其数据(对象)的引用,而值类型的变量直接包含其数据。 对于引用类型,两种变量可引用同一对…...
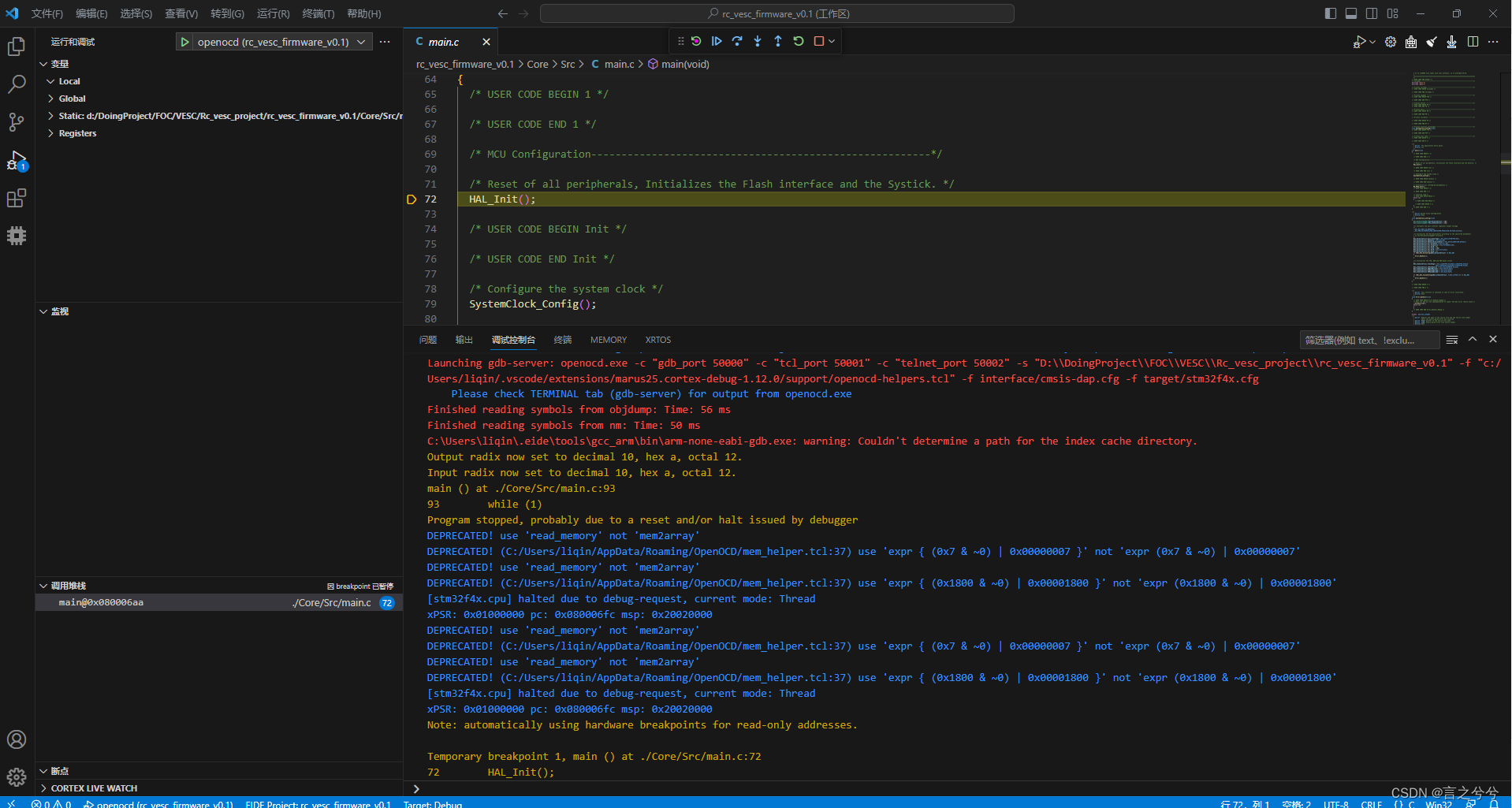
STM32CubeMX+VSCODE+EIDE+RT-THREAD 工程创建
Eide环境搭建暂且不表,后续补充。主要记录下Vscode环境下 创建Rt-thread工程的过程。分别介绍STM32CubeMX添加rtt支持包的方式和手动添加rtt kernel方式。STM32CubeMX生成工程的时候有"坑",防止下次忘记,方便渡一下有缘人ÿ…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

MVC 数据库
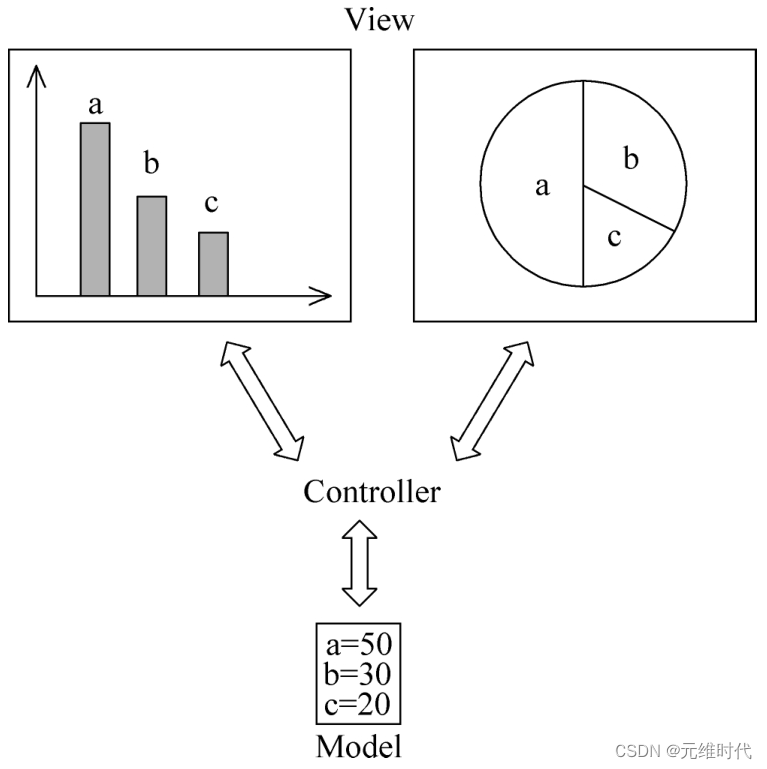
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

【若依】框架项目部署笔记
参考【SpringBoot】【Vue】项目部署_no main manifest attribute, in springboot-0.0.1-sn-CSDN博客 多一个redis安装 准备工作: 压缩包下载:http://download.redis.io/releases 1. 上传压缩包,并进入压缩包所在目录,解压到目标…...
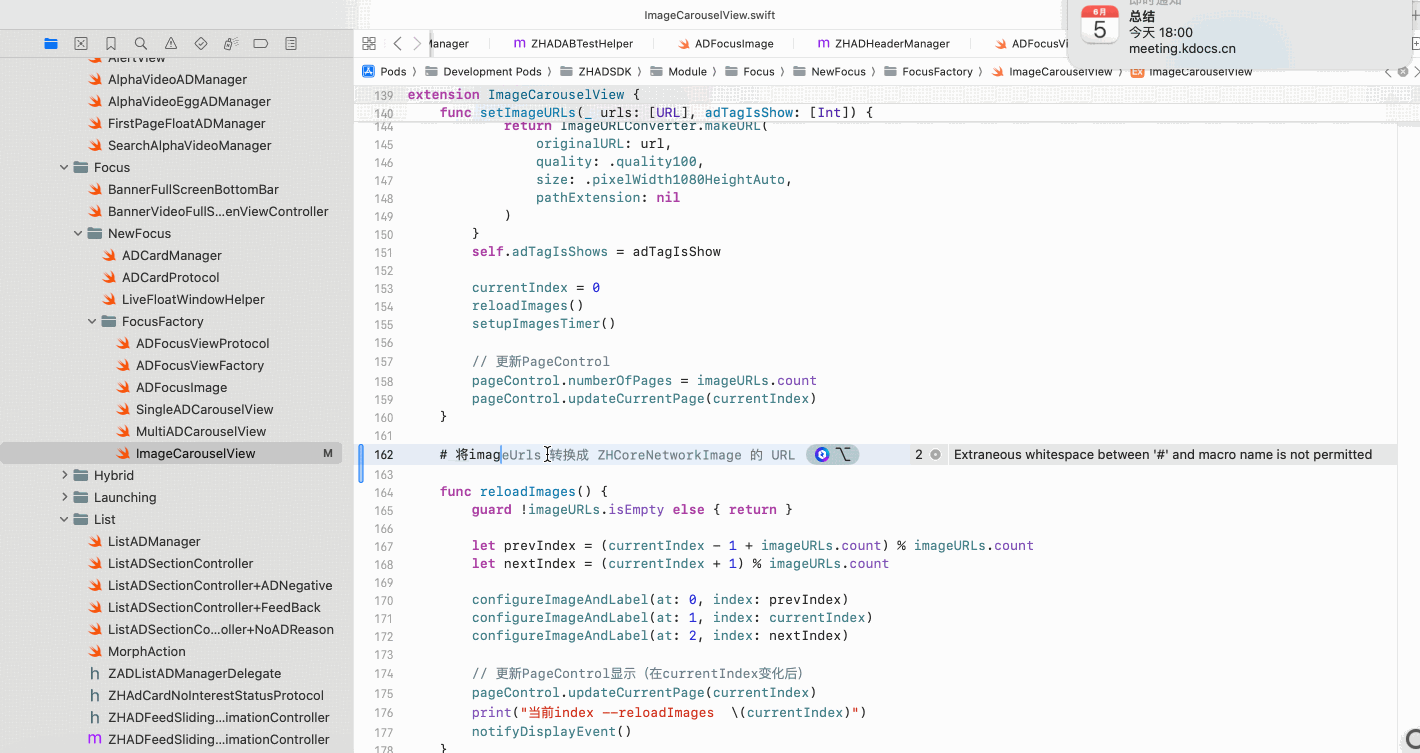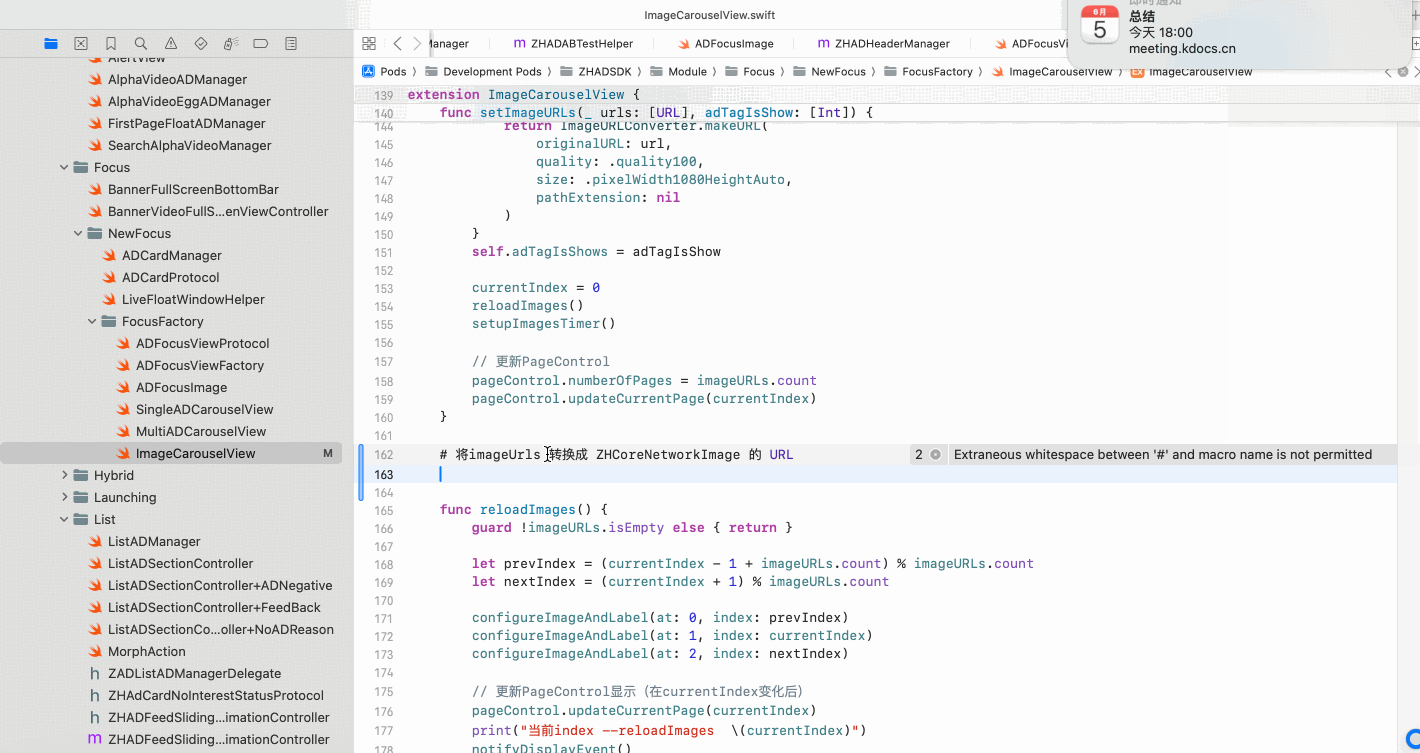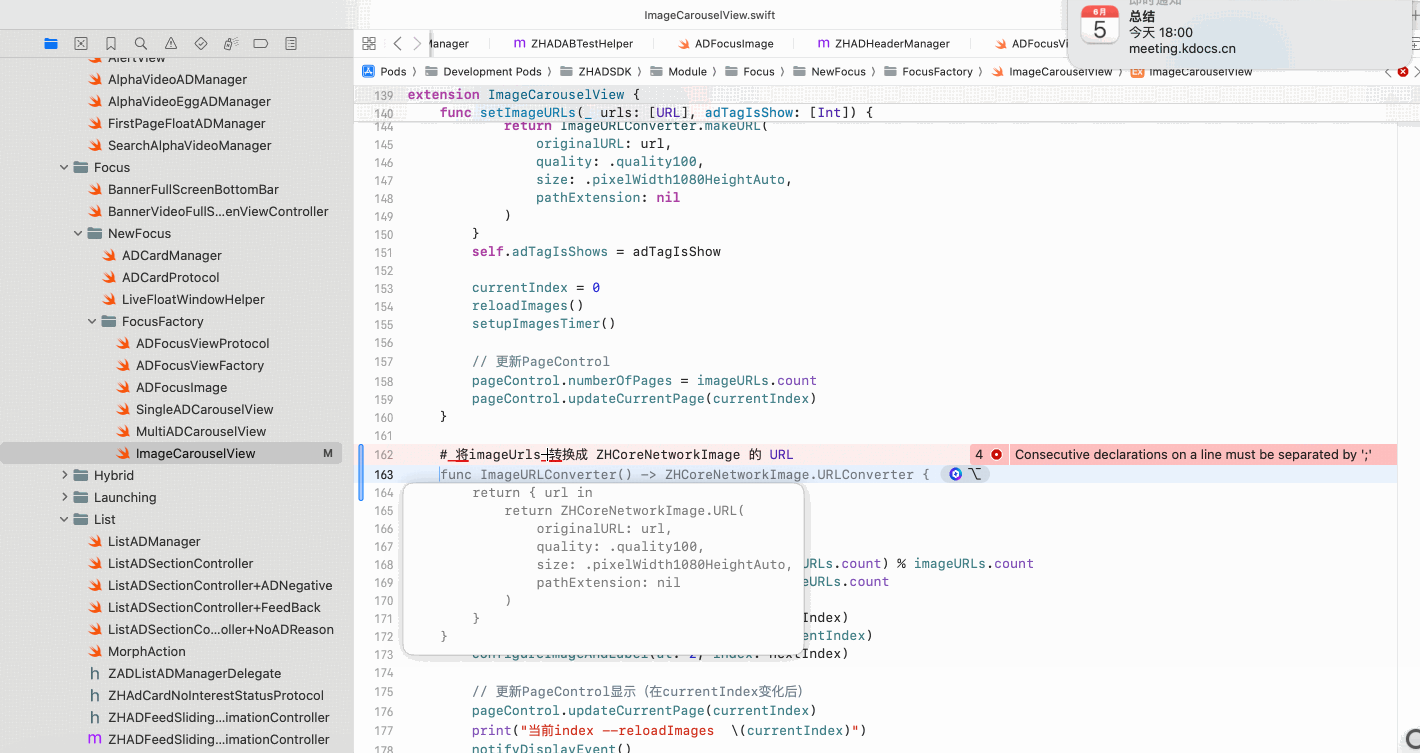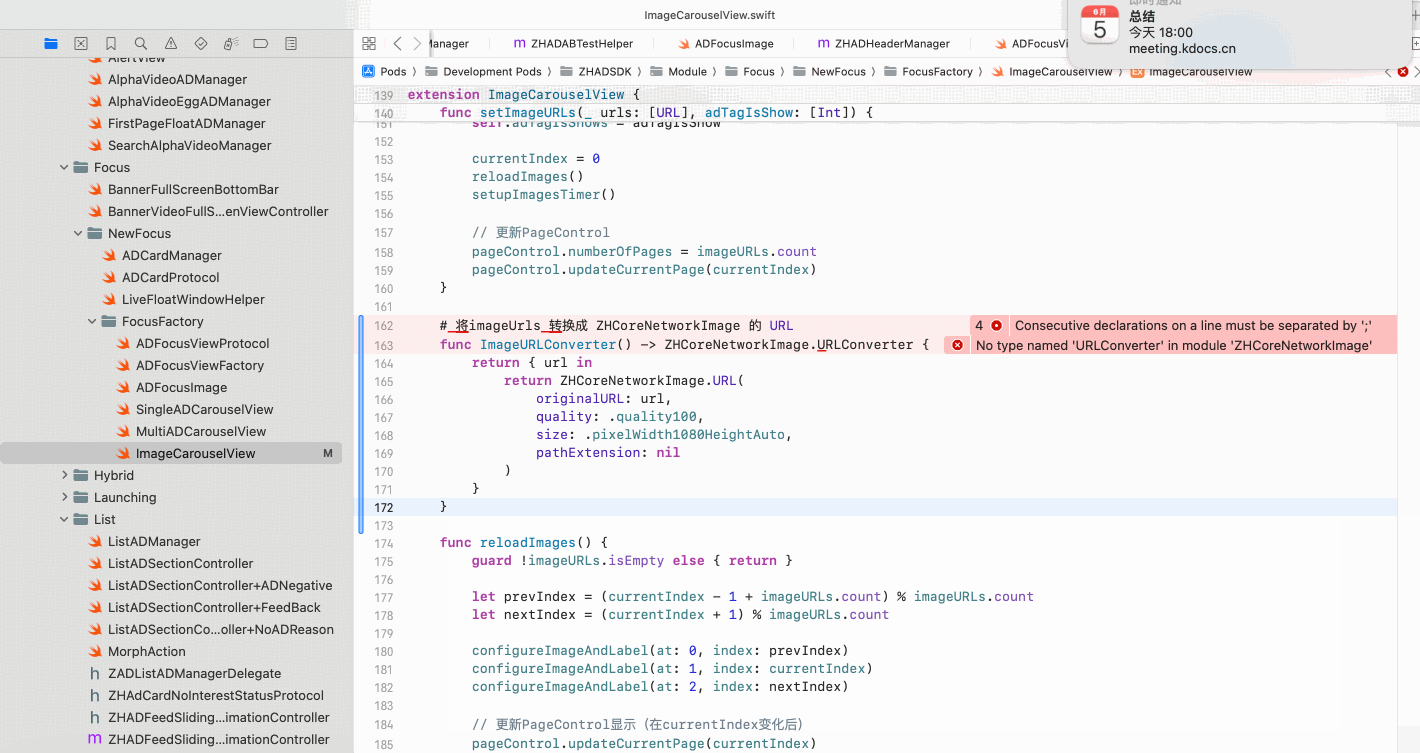
Copilot for Xcode (iOS的 AI辅助编程)
Copilot for Xcode 简介Copilot下载与安装 体验环境要求下载最新的安装包安装登录系统权限设置 AI辅助编程生成注释代码补全简单需求代码生成辅助编程行间代码生成注释联想 代码生成 总结 简介 尝试使用了Copilot,它能根据上下文补全代码,快速生成常用…...

__VUE_PROD_HYDRATION_MISMATCH_DETAILS__ is not explicitly defined.
这个警告表明您在使用Vue的esm-bundler构建版本时,未明确定义编译时特性标志。以下是详细解释和解决方案: 问题原因: 该标志是Vue 3.4引入的编译时特性标志,用于控制生产环境下SSR水合不匹配错误的详细报告1使用esm-bundler…...
