当前位置： 首页 > news >正文

Codejock Task Panel ActiveX Crack

news 2026/2/7 12:44:50

Codejock Task Panel ActiveX Crack

　　ActiveX COM的Codejock任务面板为Windows开发人员提供了一个复杂的Office任务面板，类似于在Microsoft Office和Windows资源管理器中看到的内容。TaskPanel甚至可以用作Visual Studio风格的工具箱。

　　功能概述

　　ActiveX COM的Codejock任务面板提供了几个选项可供选择，包括项目类型、组标题、动画、可扩展组、页边距、Office和Visual Studio主题支持、工具箱布局、拖放、热跟踪等。任务面板包含在用于ActiveX COM的Suite Pro中。

 

　　Office和资源管理器任务面板

　　任务面板控件

　　项目类型

　　组标题

　　特殊群体

　　动画

　　可扩展组

　　保证金

　　VS.NET样式工具箱控件

　　工具箱控件

　　工具箱布局

　　拖放项目

　　开关按钮

　　图标大小

　　热跟踪

　　行为

相关文章：

Codejock Task Panel ActiveX Crack

Codejock Task Panel ActiveX Crack ActiveX COM的Codejock任务面板为Windows开发人员提供了一个复杂的Office任务面板，类似于在Microsoft Office和Windows资源管理器中看到的内容。TaskPanel甚至可以用作Visual Studio风格的工具箱。 功能概述 ActiveX COM的Codejo…...

编程日记 2023/8/7 11:34:37

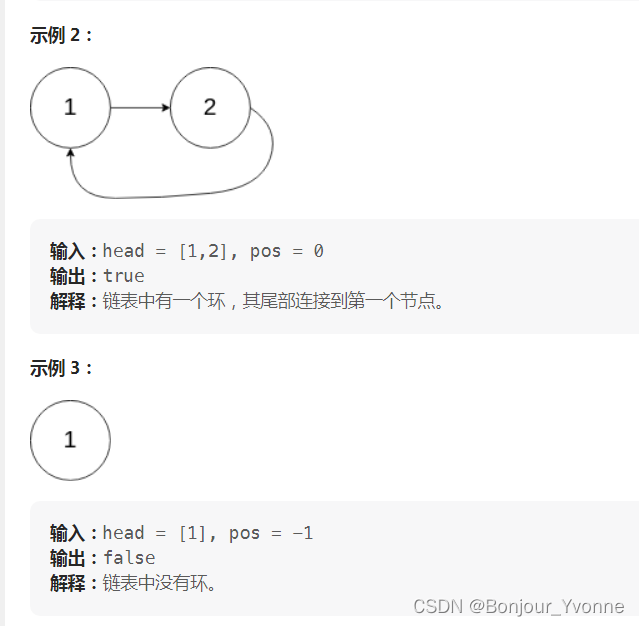
LeetCode 热题 100 JavaScript--141. 环形链表

给你一个链表的头节点 head ，判断链表中是否有环。 如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（…...

编程日记 2023/8/7 11:33:36

文字转语音

键盘获取文字，转化为语音后保存本地 from win32com.client import Dispatch from comtypes.client import CreateObject from comtypes.gen import SpeechLib speakerDispatch(SAPI.SpVoice) speaker.Speak(请输入你想转化的文字) datainput(请输入：)#s…...

编程日记 2023/8/7 11:32:34

让ELK在同一个docker网络下通过名字直接访问

1. docker网络 参考https://blog.csdn.net/lihongbao80/article/details/108019773 https://www.freecodecamp.org/chinese/news/how-to-get-a-docker-container-ip-address-explained-with-examples/ 默认网络有三种，分别是 1、bridge模式，–netbridge(…...

编程日记 2023/8/7 11:31:33

EventBus 开源库学习（一）

一、概念 EventBus是一款在 Android 开发中使用的发布-订阅事件总线框架，基于观察者模式，将事件的接收者和发送者解耦，简化了组件之间的通信，使用简单、效率高、体积小。 一句话：用于Android组件间通信的。 二、原理…...

编程日记 2023/8/7 11:30:32

车载以太网SOME/IP的个人总结

如何实现CAN-SOME/IP通信路由测试 (qq.com) AutoSAR SOMEIP与SOC vsomeip通讯 (qq.com) 利用commonAPI和vSomeip对数据进行序列化 (qq.com) Vector - CANoe - VCDL与SomeIP (qq.com) 使用Wireshark 查看SOMEIP的方法 (qq.com) 基于AutoSAR的车载以太网测试 - SOMEIP之ECU做…...

编程日记 2023/8/7 11:29:29

vue2.29-Vue3跟vue2的区别

1、vue3介绍 更新（和重写）Vue的主要版本时，主要考虑两点因素：首先是新的JavaScript语言特性在主流浏览器中的受支持水平；其次是当前代码库中随时间推移而逐渐暴露出来的一些设计和架构问题。 相较于vue2，vu…...

编程日记 2023/8/7 11:28:25

【深度学习】分类和分割常见损失函数

分类 分类是一种监督机器学习任务，其中训练模型来预测给定输入数据点的类或类别。分类旨在学习从输入特征到特定类或类别的映射。 有不同的分类任务，例如二元分类、多类分类和多标签分类。 二元分类是一项训练模型来预测两个类别之一的任务&#xff0c…...

编程日记 2023/8/7 11:27:24

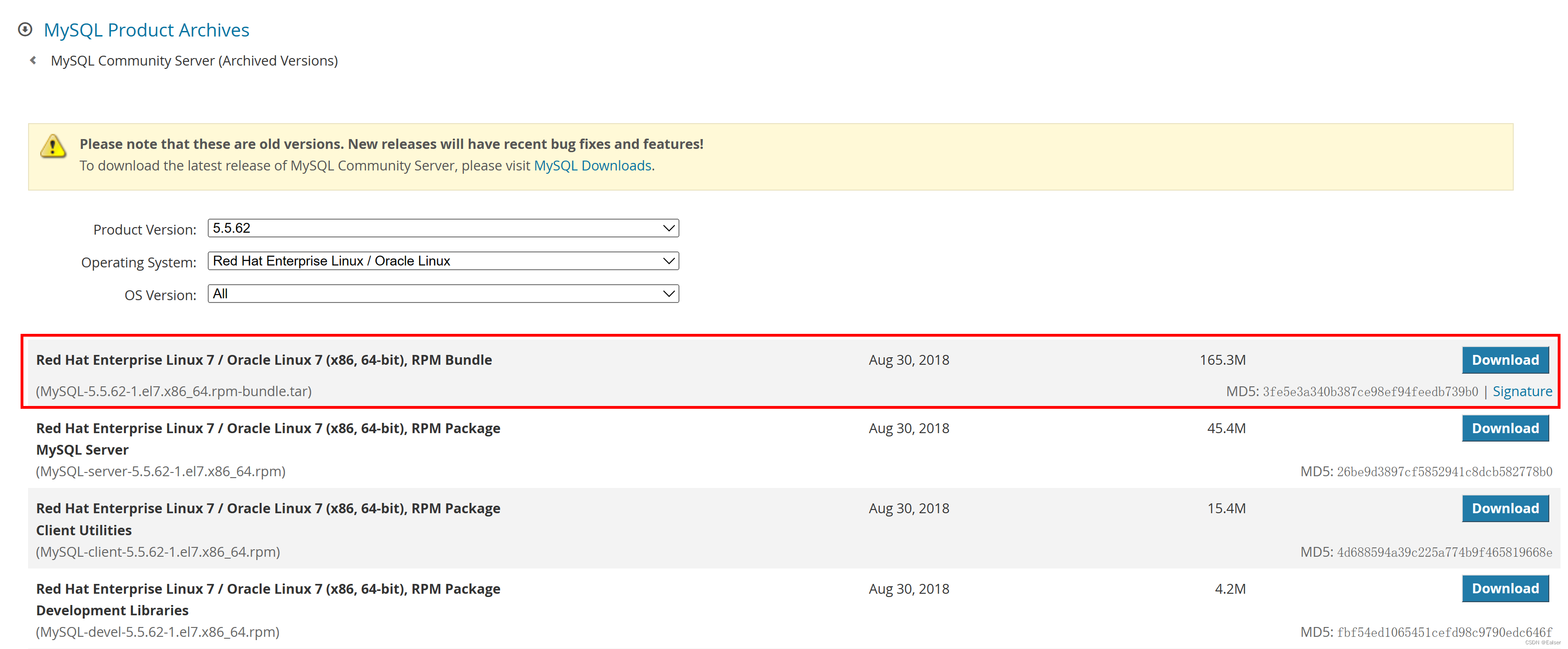
Redhat Linux 安装MySQL安装手册

Redhat安装MySQL安装手册 1 下载2 上传服务器、解压并安装3 安装安装过程1：MySQL-shared-5.6.51-1.el7.x86_64.rpm安装过程2：MySQL-shared-compat-5.6.51-1.el7.x86_64.rpm安装过程3：MySQL-server-5.6.51-1.el7.x86_64.rpm安装过程4&#xff…...

编程日记 2023/8/7 11:26:22

题目：2303.计算应缴税款总额

​​题目来源： leetcode题目，网址：2303. 计算应缴税款总额 - 力扣（LeetCode） 解题思路： 按要求计算即可。注意最多产生 n1 个不同区间内的税款即可。 解题代码： class Solution {public doub…...

编程日记 2023/8/7 11:25:21

Kotlin 1.9.0 发布：带来多项新特性，改进 Multiplatform/Native 支持

新特性 Kotlin 的最新版本引入了许多新的语言特性&#xff0c;包括用于开放范围的…<操作符、扩展正则表达式等。此外&#xff0c;它还改进了 Kotlin Multiplatform 和 Kotlin/Native 支持。 Kotlin 1.9 稳定了与枚举类关联的 entries 属性&#xff0c;它会返回所定义的枚…...

编程日记 2023/8/7 11:24:19

接口测试——认知（一）

目录 引言 环境准备 1. 为什么要进行接口测试 2. 什么是接口 3. 接口测试与功能测试的区别 引言 为什么要做接口自动化测试&#xff1f; 在当前互联网产品迭代频繁的背景下&#xff0c;回归测试的时间越来越少&#xff0c;很难在每个迭代都对所有功能做完整回归。 但接…...

编程日记 2023/8/7 11:23:18

剑指 Offer 10- I. 斐波那契数列

写一个函数&#xff0c;输入 n &#xff0c;求斐波那契&#xff08;Fibonacci&#xff09;数列的第 n 项&#xff08;即 F(N)&#xff09;。斐波那契数列的定义如下&#xff1a; F(0) 0, F(1) 1 F(N) F(N - 1) F(N - 2), 其中 N > 1. 斐波那契数列由 0 和 1 开始&am…...

编程日记 2023/8/7 11:22:14

洪水填充算法详解

&#x1f61c;作 者&#xff1a;是江迪呀✒️本文关键词&#xff1a;算法、前端、JavaScript、HTML、洪水填充算法☀️每日 一言&#xff1a;不以物喜&#xff0c;不以己悲 一、前言 当象一个容器中注水时&#xff0c;无论容器的结构如何复杂&#xff0c;注入的水…...

编程日记 2023/8/7 11:21:13

ubuntu18.04安装docker及docker基本命令的使用

官网安装步骤&#xff1a;https://docs.docker.com/desktop/install/ubuntu/ docker快速入门教程 Ubuntu-Docker安装和使用 docker官网 docker-hub仓库 1、常用指令 &#xff08;1&#xff09;镜像操作 # ############################# 以nginx为例 docker images docker p…...

编程日记 2023/8/7 11:20:12

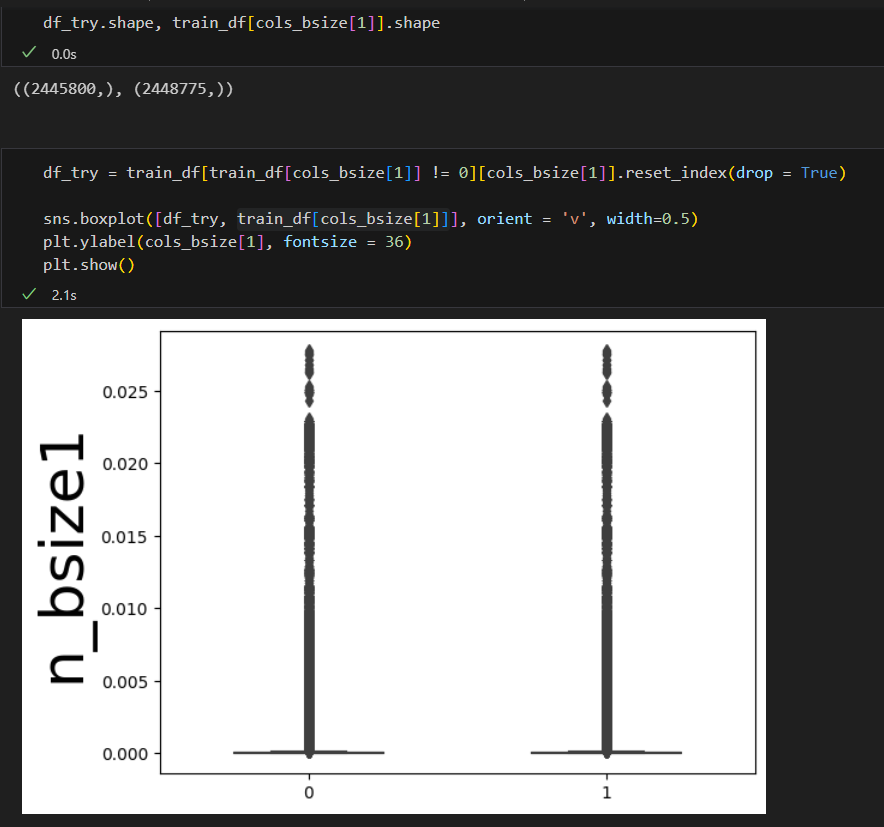
DataWhale 机器学习夏令营第二期——AI量化模型预测挑战赛 学习记录

DataWhale 机器学习夏令营第二期 学习记录一 (2023.08.06)1. 问题建模1.1 赛事数据数据集情况数据中缺失值类别和数值特征的基本分布 1.2 评价指标中间价的计算方式价格移动方向说明 1.3 线下验证 DataWhale 机器学习夏令营第二期 ——AI量化模型预测挑战赛 已跑通baseline&…...

编程日记 2023/8/7 11:19:11

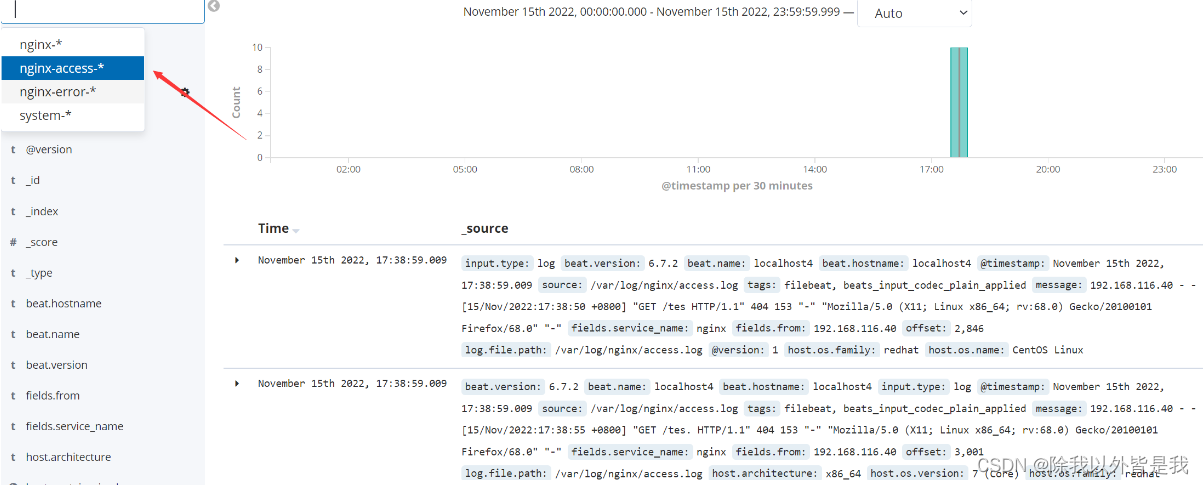
简单认识ELK日志分析系统

一. ELK日志分析系统概述 1.ELK 简介 ELK平台是一套完整的日志集中处理解决方案&#xff0c;将 ElasticSearch、Logstash 和 Kiabana 三个开源工具配合使用&#xff0c; 完成更强大的用户对日志的查询、排序、统计需求。 好处&#xff1a; &#xff08;1&#xff09;提高安全…...

编程日记 2023/8/7 11:18:10

【算法笔记】深度优先遍历-解决排列组合问题-

深度优先遍历-解决排列组合问题 问题1&#xff1a; 假设袋子里有编号为1,2,…,m这m个球。现在每次从袋子中取一个球记下编号&#xff0c;放回袋中再取&#xff0c;取n次作为一组&#xff0c;枚举所有可能的情况。 分析&#xff1a; 每一次取都有m种可能的情况&#xff0c;因此…...

编程日记 2023/8/7 11:17:09

【雕爷学编程】Arduino动手做（184）---快餐盒盖，极低成本搭建机器人实验平台2

吃完快餐粥&#xff0c;除了粥的味道不错之外&#xff0c;我对个快餐盒的圆盖子产生了兴趣&#xff0c;能否做个极低成本的简易机器人呢&#xff1f;也许只需要二十元左右 知识点&#xff1a;轮子&#xff08;wheel&#xff09; 中国词语。是用不同材料制成的圆形滚动物体。简…...

编程日记 2023/8/7 11:16:08

应急响应-勒索病毒的处理思路

0x00 关于勒索病毒的描述 勒索病毒入侵方式&#xff1a;服务弱口令&#xff0c;未授权&#xff0c;邮件钓鱼&#xff0c;程序木马植入&#xff0c;系统漏洞等 勒索病毒的危害&#xff1a;主机文件被加密&#xff0c;且几乎难以解密&#xff0c;对主机上的文件信息以及重要资产…...

编程日记 2023/8/7 11:15:06

设计模式和设计原则回顾

设计模式和设计原则回顾 23种设计模式是设计原则的完美体现，设计原则设计原则是设计模式的理论基石， 设计模式 在经典的设计模式分类中（如《设计模式：可复用面向对象软件的基础》一书中），总共有23种设计模式，分为三大类： 一、创建型模式（5种） 1. 单例模式（Sing…...

编程新知 2025/12/14 20:57:41

Day131 | 灵神 | 回溯算法 | 子集型 子集

Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣&#xff08;LeetCode&#xff09; 思路&#xff1a; 笔者写过很多次这道题了&#xff0c;不想写题解了&#xff0c;大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

编程新知 2026/1/23 12:37:51

Mybatis逆向工程，动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件

今天呢&#xff0c;博主的学习进度也是步入了Java Mybatis 框架&#xff0c;目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学&#xff0c;希望能对大家有所帮助&#xff0c;也特别欢迎大家指点不足之处&#xff0c;小生很乐意接受正确的建议&…...

编程新知 2026/1/31 15:00:15

UE5 学习系列（三）创建和移动物体

这篇博客是该系列的第三篇&#xff0c;是在之前两篇博客的基础上展开&#xff0c;主要介绍如何在操作界面中创建和拖动物体&#xff0c;这篇博客跟随的视频链接如下&#xff1a; B 站视频&#xff1a;s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

编程新知 2026/1/24 10:00:31

selenium学习实战【Python爬虫】

selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

编程新知 2026/2/4 12:52:32

JAVA后端开发——多租户

数据隔离是多租户系统中的核心概念&#xff0c;确保一个租户&#xff08;在这个系统中可能是一个公司或一个独立的客户&#xff09;的数据对其他租户是不可见的。在 RuoYi 框架&#xff08;您当前项目所使用的基础框架&#xff09;中&#xff0c;这通常是通过在数据表中增加一个…...

编程新知 2025/12/18 8:35:12

让回归模型不再被异常值“带跑偏“，MSE和Cauchy损失函数在噪声数据环境下的实战对比

在机器学习的回归分析中&#xff0c;损失函数的选择对模型性能具有决定性影响。均方误差&#xff08;MSE&#xff09;作为经典的损失函数&#xff0c;在处理干净数据时表现优异&#xff0c;但在面对包含异常值的噪声数据时&#xff0c;其对大误差的二次惩罚机制往往导致模型参数…...

编程新知 2026/1/28 2:18:46

短视频矩阵系统文案创作功能开发实践，定制化开发

在短视频行业迅猛发展的当下&#xff0c;企业和个人创作者为了扩大影响力、提升传播效果&#xff0c;纷纷采用短视频矩阵运营策略&#xff0c;同时管理多个平台、多个账号的内容发布。然而&#xff0c;频繁的文案创作需求让运营者疲于应对&#xff0c;如何高效产出高质量文案成…...

编程新知 2026/2/1 8:24:29

力扣热题100 k个一组反转链表题解

题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

编程新知 2026/1/31 8:25:07

MySQL：分区的基本使用

目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区&#xff08;Partitioning&#xff09;是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分&#xff08;分区&#xff09;可以独立存储、管理和优化&#xff0c;…...

编程新知 2026/2/2 18:52:32