【深度学习】分类和分割常见损失函数
分类
分类是一种监督机器学习任务,其中训练模型来预测给定输入数据点的类或类别。分类旨在学习从输入特征到特定类或类别的映射。
有不同的分类任务,例如二元分类、多类分类和多标签分类。
-
二元分类是一项训练模型来预测两个类别之一的任务,例如“垃圾邮件”或“非垃圾邮件”。
-
多类分类是一项训练模型来预测图像的多个类之一的任务,例如“狗”、“猫”和“鸟”。
-
多标签分类是一项训练模型来预测单个数据点的多个标签的任务,例如公园里狗的图像的“狗”和“户外”。
分类算法可以基于决策树、朴素贝叶斯、k 最近邻、支持向量机、随机森林、梯度提升、神经网络等技术。
最常见损失函数:BCE、WBCE、CCE、Sparse Categorical Cross-entropy Loss、Cross-Entropy loss with label smoothing、Focal loss、Hinge Loss。
Binary Cross Entropy (BCE)
二元交叉熵(BCE),也称为对数损失,是二元分类问题常用的损失函数。它测量类别的预测概率与真实类别标签之间的差异。
交叉熵是信息论中的一个众所周知的概念,通常用于测量两个概率分布之间的差异。在二元分类中,真实类别通常由 one-hot 编码向量表示,其中真实类别的值为 1,另一类别的值为 0。预测概率由预测概率向量表示每个类别,其中真实类别的预测概率由 p ( y = 1 ∣ x ) p(y = 1|x) p(y=1∣x) 表示,其他类别的预测概率由 p ( y = 0 ∣ x ) p(y = 0|x) p(y=0∣x) 表示。
损失函数定义为:
L ( y , p ) = − ( y l o g ( p ) + ( 1 − y ) l o g ( 1 − p ) ) L(y, p) = −(y log(p) + (1 − y) log(1 − p)) L(y,p)=−(ylog(p)+(1−y)log(1−p))
其中
{ − l o g ( p ) y = 1 − l o g ( 1 − p ) y = 0 \left\{\begin{matrix} −log(p) & y = 1\\ −log(1 − p)&y = 0 \end{matrix}\right. {−log(p)−log(1−p)y=1y=0
其中 y y y 是真实类标签(0 或 1), p p p 是正类的预测概率。当预测概率 p p p 等于真实类标签 y y y 时,损失函数最小化。
二元交叉熵损失具有几个理想的特性,例如易于计算、可微分以及提供模型输出的概率解释。它还提供了平滑的优化表面,并且与其他损失函数相比对异常值不太敏感。然而,它对类不平衡问题很敏感,当一个类的样本数量显着大于另一类时就会发生这种问题。对于这些情况,可以使用加权二元交叉熵Weighted Binary Cross Entropy (WBCE)。
Weighted Binary Cross Entropy (WBCE)
标准二元交叉熵损失函数的变体,其中在损失计算过程中考虑每个样本的权重。这在样本分布不平衡的情况下很有用。
在标准二元交叉熵损失中,损失被计算为给定预测概率的真实标签的负对数似然。在加权二元交叉熵(WBCE)中,为每个样本分配一个权重,每个样本的损失计算如下:
L = − ( w i ⋅ y l o g ( p ) + w i ( 1 − y ) l o g ( 1 − p ) ) L = −(w_i · ylog(p) + w_i(1 − y)log(1 − p)) L=−(wi⋅ylog(p)+wi(1−y)log(1−p))
其中 w i w_i wi是分配给第 i i i 个样本的权重, y y y 是真实标签, p p p 是正类的预测概率。
通过为代表性不足的类别的样本分配更高的权重,鼓励模型更多地关注这些样本,并且可以提高模型的整体性能。
Categorical Cross-entropy Loss (CCE)
分类交叉熵(CCE)又称负对数似然损失或多类对数损失,是一种用于多类分类任务的函数。它衡量的是预测概率分布与真实分布之间的差异。
鉴于预测的概率分布,它被定义为真实类别的平均负对数似然。分类交叉熵损失的公式表示为
L = − 1 N ∑ i = 1 N ∑ j = 1 C y i , j l o g ( p i , j ) L=-\frac{1}{N} \sum_{i=1}^{N} \sum_{j=1}^{C} y_{i,j}log(p_i,j) L=−N1i=1∑Nj=1∑Cyi,jlog(pi,j)
其中 N N N 是样本数, C C C 是类别数, y y y 是真实标签, p p p 是真实类别的预测概率。计算每个样本的损失并在整个数据集上取平均值。
真实标签是传统分类交叉熵损失中的one-hot编码向量,其中真实类别对应的元素为1,所有其他元素为0。但是,在某些情况下,表示真实类别更方便类作为整数,其中整数值对应于导致接下来讨论的稀疏分类交叉熵损失的真实类的索引。
Sparse Categorical Cross-entropy Loss
用于多类分类任务的分类交叉熵损失的变化,其中类被编码为整数而不是单热编码向量。鉴于真实标签以整数形式提供,我们直接使用提供的标签索引选择正确的类,而不是对所有可能的类求和。因此每个例子的损失计算如下:
H ( y , y ^ ) = − l o g ( y i , y i ^ ) H(y, \hat{y} ) = − log(\hat {{y_{_{i} ,y_i} }}) H(y,y^)=−log(yi,yi^)
最终的稀疏分类交叉熵损失是所有样本的平均值
H ( Y , Y ^ ) = − 1 n ∑ i = 1 n l o g ( y i , y i ^ ) H(Y, \hat{Y} ) =-\frac{1}{n} \sum_{i=1}^{n} log(\hat{{y_{_{i} ,y_i} } }) H(Y,Y^)=−n1i=1∑nlog(yi,yi^)
其中 y i y_i yi 是第 i i i 个样本的真实类别,并且 y i , y i ^ \hat{y_{_{i} ,y_i}} yi,yi^是第 i 个样本对于正确类别 y i y_i yi 的预测概率。
Cross-Entropy loss with label smoothing
在带有标签平滑的交叉熵损失中,通过向真实标签添加一个小值并从所有其他标签中减去相同的值来平滑标签。这有助于通过鼓励模型产生更多不确定的预测来减少模型的过度自信。
其背后的动机是,在训练模型时,通常对其预测过于自信,特别是在对大量数据进行训练时。这种过度自信可能会导致在看不见的数据上表现不佳。标签平滑通过鼓励模型做出不太自信的预测来帮助缓解这个问题。
带标签平滑的交叉熵损失的公式与标准分类交叉熵损失类似,但在真实标签上添加了一个小 epsilon,并从所有其他标签中减去。公式由下式给出:
L ( y , y ^ ) = ∑ c = 1 C [ ( 1 − ϵ ) y c l o g y c ^ + ϵ C l o g y ^ ] L(y, \hat{y} ) =\sum_{c=1}^{C}\left [ (1 − ϵ)y_c log \hat {y_c} + \frac{ϵ}{C}log \hat y \right ] L(y,y^)=c=1∑C[(1−ϵ)yclogyc^+Cϵlogy^]
其中 y y y 是真实标签, y ^ \hat y y^ 是预测标签, C C C 是类数, ϵ ϵ ϵ 是平滑值。通常, ϵ ϵ ϵ 设置为一个较小的值,例如 0.1 或 0.2。
标签平滑并不总能提高性能,通常会尝试不同的 epsilon 值来找到特定任务和数据集的最佳值。
Focal Loss
Focal Loss 是标准交叉熵损失的一种变体,它解决了类别不平衡的问题,当正样本(感兴趣的对象)的数量远小于负样本(背景)的数量时就会发生这种情况。在这种情况下,模型往往会关注负样本而忽略正样本,从而导致性能不佳。Focal Loss通过降低简单负样本的权重并提高困难正样本的权重来解决这个问题。
Focal Loss定义为
F L ( p t ) = − α t ( 1 − p t ) γ l o g ( p t ) FL(p_t) = −α_t(1 − p_t)^γ log(p_t) FL(pt)=−αt(1−pt)γlog(pt)
其中 p t p_t pt 是真实类别的预测概率, α t α_t αt 是控制每个样本重要性的权重因子, γ γ γ 是控制简单样本加权速率的聚焦参数。
权重因子 α t α_t αt 通常设置为逆类别频率,以平衡所有类别的损失。聚焦参数 γ γ γ 通常设置为 2 到 4 之间的值,以给予困难示例更多的权重
在 原始论文Focal loss for dense object detection 中,作者使用 sigmoid 激活函数进行二元分类,使用交叉熵损失进行多类分类。焦点损失与这些损失函数相结合,可以提高对象检测和语义分割模型的性能。在最近的工作中,Focal Loss 已被用于对象检测、语义、实例分割和人体姿势估计。
Hinge Loss
铰链损失(Hinge Loss)是用于最大边缘分类的流行函数,通常用于支持向量机 (SVM),例如在一对多分类中,我们将实例分类为属于我们想要提供的多个类别和情况之一误差幅度。
单个实例的铰链损失函数可以表示为
L ( y , f ( x ) ) = m a x ( 0 , 1 − y ⋅ f ( x ) ) L(y, f (x)) = max(0, 1 − y · f (x)) L(y,f(x))=max(0,1−y⋅f(x))
其中 y y y 是实例的真实标签,在二元分类问题中应为 -1 或 1。 f ( x ) f (x) f(x) 是实例 x x x 的预测输出。原始边距为 y ⋅ f ( x ) y · f (x) y⋅f(x)。
如果实例位于边距的正确一侧,则铰链损失为 0。对于边缘错误一侧的数据,损失与距边缘的距离成正比。
分割
常见的损失函数包括交叉熵损失、交并集 (IoU) 损失、Focal Loss、Dice 损失、Tversky 损失和 Lovász 损失。
分割的Cross Entropy Loss
分割的交叉熵损失衡量预测分割图和真实分割图 (GT) 之间的差异。交叉熵损失是通过逐像素比较预测和真实分割图来计算的。它被定义为给定预测分割图的真实分割图的负对数似然。交叉熵损失使用以下公式计算:
− 1 N ∑ i = 1 N ∑ c = 1 C y i , c l o g ( p i , c ) -\frac{1}{N} \sum_{i=1}^{N} \sum_{c=1}^{C} y_{i,c}log(p_{i,c}) −N1i=1∑Nc=1∑Cyi,clog(pi,c)
其中 N N N 是图像中的像素总数, C C C 是类别数, y y y 是真实分割图, p p p 是预测分割图。 y y y和 p p p的值应该在0和1之间并且总和为1。交叉熵损失越低,预测越好。
分割的Intersection Over Union (IoU) loss
Intersection Over Union(IoU)损失是语义分割任务中常用的损失函数和评估指标。目标是预测给定图像的每像素分割掩模。 IoU 损失也称为 Jaccard 损失或 Jaccard 指数 (JI),定义为预测掩模和真实掩模的交集与预测掩模和真实掩模的并集之比。 IoU 损失是按像素计算的,最终损失是图像中所有像素的平均 IoU。
IoU 损失可以在数学上定义为:
I o U = 1 n ∑ i = 1 n y i ∩ y i ^ y i ∪ y i ^ IoU=\frac{1}{n} \sum_{i=1}^{n} \frac{y_i\cap \hat {y_i}}{y_i \cup \hat {y_i}} IoU=n1i=1∑nyi∪yi^yi∩yi^
其中 y i y_i yi 是像素 i i i 的真实掩码, y i ^ \hat {y_i} yi^是预测掩码, y i ∩ y i ^ y_i\cap \hat {y_i} yi∩yi^是真实掩码和预测掩码的交集, y i ∪ y i ^ y_i \cup \hat {y_i} yi∪yi^是真实掩码和预测掩码的并集。
IoU 在各种语义分割工作中通常用作损失函数和评估指标。
Dice Loss
Dice Loss,也称为Dice相似系数,用于评估预测分割掩模与真实分割掩模之间的相似性。损失函数定义为
L = 1 − 2 ⋅ i n t e r s e c t i o n ( p r e d , g t ) ∣ p r e d ∣ + ∣ g t ∣ L = 1 − \frac{2 · intersection(pred, gt) }{|pred| + |gt|} L=1−∣pred∣+∣gt∣2⋅intersection(pred,gt)
其中 p r e d pred pred 是预测分割掩码, g t gt gt 是真实分割掩码, i n t e r s e c t i o n ( p r e d , g t ) intersection(pred, gt) intersection(pred,gt) 是预测和真实况掩码交集中的像素数, ∣ p r e d ∣ |pred| ∣pred∣和 ∣ g t ∣ |gt| ∣gt∣分别是预测掩模和真实掩模中的像素总数。
Dice loss 广泛应用于医学成像,其目标是高精度分割图像中的结构。
Tversky loss
Tversky Loss是 Dice Loss的变体,常用于图像分割任务。它被定义为
T v e r s k y ( A , B ) = ∣ A ∩ B ∣ ∣ A ∩ B ∣ + α ∣ A − B ∣ + β ∣ B − A ∣ Tversky(A, B) = \frac{|A ∩ B|}{|A ∩ B| + α|{A-B}| + β|{B-A}| } Tversky(A,B)=∣A∩B∣+α∣A−B∣+β∣B−A∣∣A∩B∣
其中 A A A 和 B B B 分别是预测和真实分割掩码, α α α 和 β β β 是用户定义的超参数,用于控制误报和误报的权重。
此损失函数与 Dice 损失类似,但它允许为误报和误报分配不同的权重,这在两类错误之间不平衡很严重的某些场景中非常有用。
Lovász Loss
Lovász Loss背后的主要思想是通过优化预测分割和真实分割之间的 Jaccard 指数或 IoU 来优化 IoU。这种损失函数在图像分割任务中特别有用,其中交并(IoU)分数非常重要。 Lovász Loss 定义为预测分割掩码与真实分割掩码之和,通过 Jaccard 指数加权如下:
L = − 1 N ∑ i − 1 N J a c c a r d ( p i , y i ) l o g ( p i ) L = − \frac{1}{N} \sum_{i-1}^{N}Jaccard(p_i, y_i) log(p_i) L=−N1i−1∑NJaccard(pi,yi)log(pi)
其中 N N N 是图像中的像素数, p p p 是预测的分割掩模, y y y 是真实分割掩模。
Lovász Loss为不可微 IoU 指标提供了可微替代指标,使其可以直接优化。
相关文章:

【深度学习】分类和分割常见损失函数
分类 分类是一种监督机器学习任务,其中训练模型来预测给定输入数据点的类或类别。分类旨在学习从输入特征到特定类或类别的映射。 有不同的分类任务,例如二元分类、多类分类和多标签分类。 二元分类是一项训练模型来预测两个类别之一的任务,…...
Redhat Linux 安装MySQL安装手册
Redhat安装MySQL安装手册 1 下载2 上传服务器、解压并安装3 安装安装过程1:MySQL-shared-5.6.51-1.el7.x86_64.rpm安装过程2:MySQL-shared-compat-5.6.51-1.el7.x86_64.rpm安装过程3:MySQL-server-5.6.51-1.el7.x86_64.rpm安装过程4ÿ…...

题目:2303.计算应缴税款总额
题目来源: leetcode题目,网址:2303. 计算应缴税款总额 - 力扣(LeetCode) 解题思路: 按要求计算即可。注意最多产生 n1 个不同区间内的税款即可。 解题代码: class Solution {public doub…...

Kotlin 1.9.0 发布:带来多项新特性,改进 Multiplatform/Native 支持
新特性 Kotlin 的最新版本引入了许多新的语言特性,包括用于开放范围的…<操作符、扩展正则表达式等。此外,它还改进了 Kotlin Multiplatform 和 Kotlin/Native 支持。 Kotlin 1.9 稳定了与枚举类关联的 entries 属性,它会返回所定义的枚…...

接口测试——认知(一)
目录 引言 环境准备 1. 为什么要进行接口测试 2. 什么是接口 3. 接口测试与功能测试的区别 引言 为什么要做接口自动化测试? 在当前互联网产品迭代频繁的背景下,回归测试的时间越来越少,很难在每个迭代都对所有功能做完整回归。 但接…...

剑指 Offer 10- I. 斐波那契数列
写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项(即 F(N))。斐波那契数列的定义如下: F(0) 0, F(1) 1 F(N) F(N - 1) F(N - 2), 其中 N > 1. 斐波那契数列由 0 和 1 开始&am…...

洪水填充算法详解
😜作 者:是江迪呀✒️本文关键词:算法、前端、JavaScript、HTML、洪水填充算法☀️每日 一言:不以物喜,不以己悲 一、前言 当象一个容器中注水时,无论容器的结构如何复杂,注入的水…...
ubuntu18.04安装docker及docker基本命令的使用
官网安装步骤:https://docs.docker.com/desktop/install/ubuntu/ docker快速入门教程 Ubuntu-Docker安装和使用 docker官网 docker-hub仓库 1、常用指令 (1)镜像操作 # ############################# 以nginx为例 docker images docker p…...
DataWhale 机器学习夏令营第二期——AI量化模型预测挑战赛 学习记录
DataWhale 机器学习夏令营第二期 学习记录一 (2023.08.06)1. 问题建模1.1 赛事数据数据集情况数据中缺失值类别和数值特征的基本分布 1.2 评价指标中间价的计算方式价格移动方向说明 1.3 线下验证 DataWhale 机器学习夏令营第二期 ——AI量化模型预测挑战赛 已跑通baseline&…...
简单认识ELK日志分析系统
一. ELK日志分析系统概述 1.ELK 简介 ELK平台是一套完整的日志集中处理解决方案,将 ElasticSearch、Logstash 和 Kiabana 三个开源工具配合使用, 完成更强大的用户对日志的查询、排序、统计需求。 好处: (1)提高安全…...

【算法笔记】深度优先遍历-解决排列组合问题-
深度优先遍历-解决排列组合问题 问题1: 假设袋子里有编号为1,2,…,m这m个球。现在每次从袋子中取一个球记下编号,放回袋中再取,取n次作为一组,枚举所有可能的情况。 分析: 每一次取都有m种可能的情况,因此…...

【雕爷学编程】Arduino动手做(184)---快餐盒盖,极低成本搭建机器人实验平台2
吃完快餐粥,除了粥的味道不错之外,我对个快餐盒的圆盖子产生了兴趣,能否做个极低成本的简易机器人呢?也许只需要二十元左右 知识点:轮子(wheel) 中国词语。是用不同材料制成的圆形滚动物体。简…...

应急响应-勒索病毒的处理思路
0x00 关于勒索病毒的描述 勒索病毒入侵方式:服务弱口令,未授权,邮件钓鱼,程序木马植入,系统漏洞等 勒索病毒的危害:主机文件被加密,且几乎难以解密,对主机上的文件信息以及重要资产…...

ChatGPT是否能够处理多模态数据和多模态对话?
ChatGPT有潜力处理多模态数据和多模态对话,这将进一步扩展其在各种应用领域中的实用性。多模态数据是指包含多种不同类型的信息,例如文本、图像、音频和视频等。多模态对话是指涉及多种媒体形式的对话交流,例如同时包含文本和图像的对话。 *…...

AcWing1171. 距离(lcatarjan)
输入样例1: 2 2 1 2 100 1 2 2 1输出样例1: 100 100输入样例2: 3 2 1 2 10 3 1 15 1 2 3 2输出样例2: 10 25 #include<bits/stdc.h> using namespace std; typedef long long ll; const int N2e55; int n,m,x,y,k,r…...
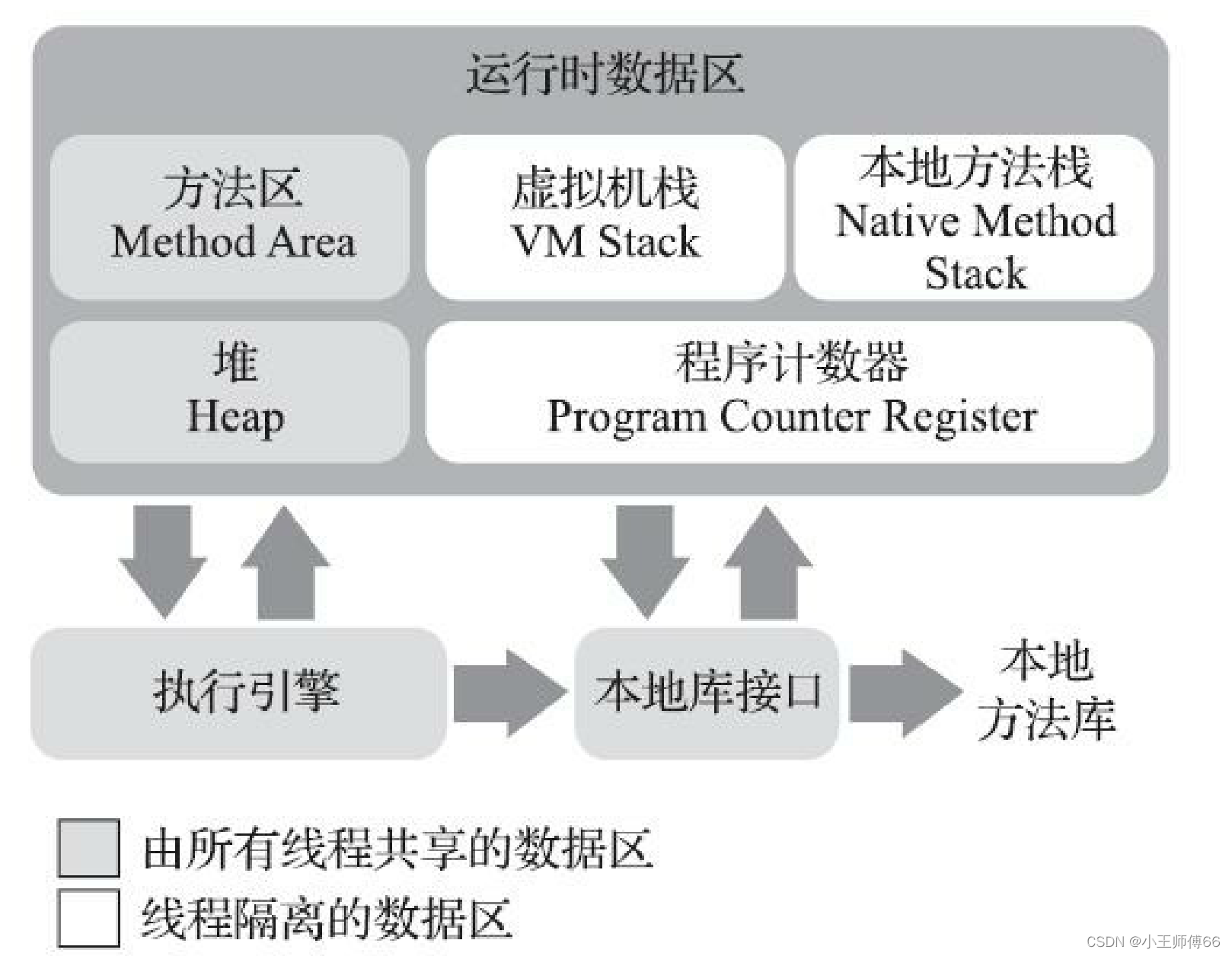
JVM-运行时数据区
目录 什么是运行时数据区? 方法区 堆 程序计数器 虚拟机栈 局部变量表 操作数栈 动态连接 运行时常量池 方法返回地址 附加信息 本地方法栈 总结: 什么是运行时数据区? Java虚拟机在执行Java程序时,将它管…...

RedisTemplate中boundHashOps的使用
1、往指定key中存储 键值 redisTemplate.boundHashOps("demo").put("1",1); 2、根据指定key中得键取出值 System.out.println(redisTemplate.boundHashOps("demo").get("1")); 3、根据指定key中得键删除 redisTemplate.boundHash…...

计算机网络-性能指标
计算机网络-性能指标 文章目录 计算机网络-性能指标简介速率比特速率 带宽吞吐量时延时延计算 时延带宽积往返时间网络利用率丢包率总结 简介 性能指标可以从不同的方面来度量计算机网络的性能 常用的计算机网络的性能指标有以下8个 速率带宽吞吐量时延时延带宽积往返时间利…...

排序第一课【插入排序】直接插入排序 与 希尔排序
目录 1. 排序的概念: 2.插入排序基本思想 3.直接插入排序 4.希尔排序 1. 排序的概念: 排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。 稳定性…...
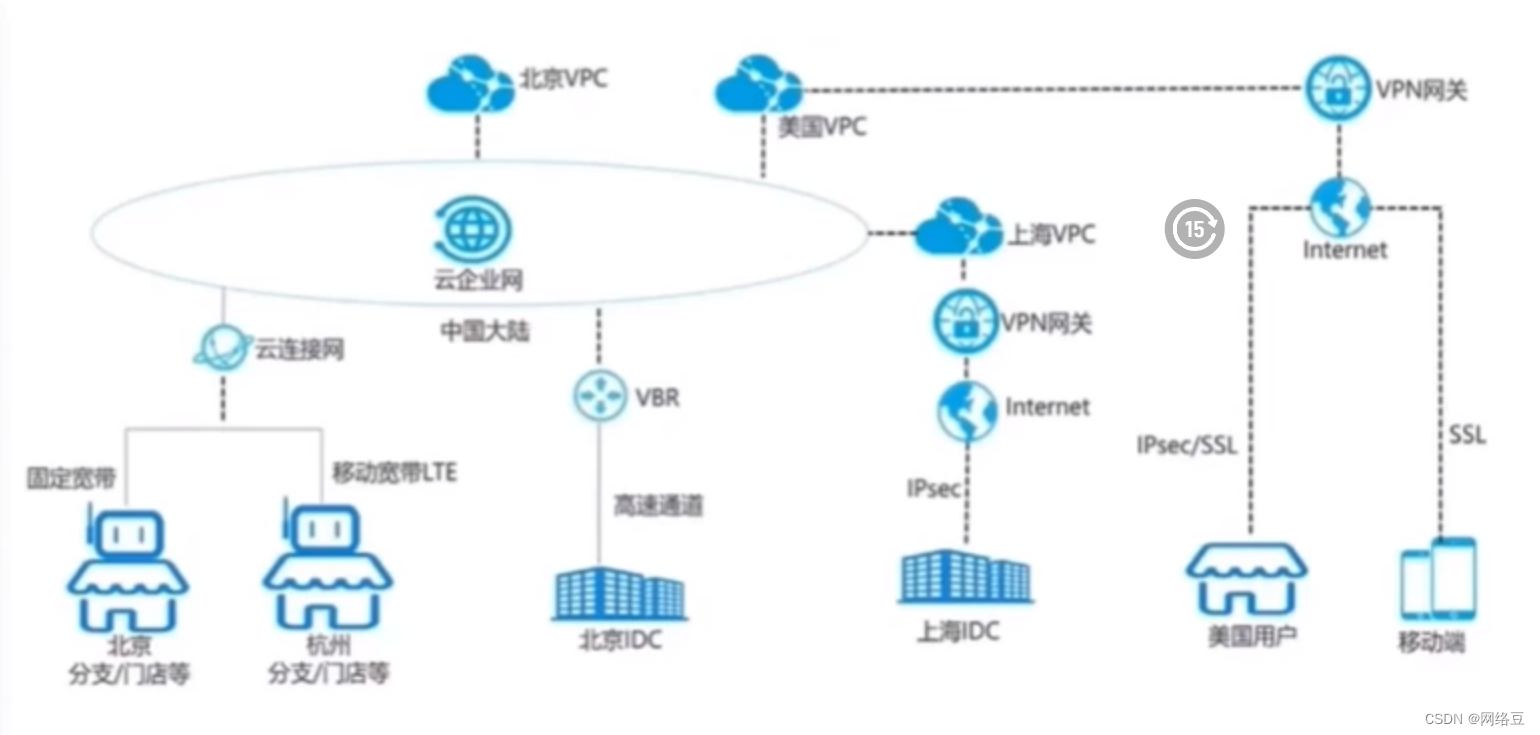
云计算——ACA学习 云计算概述
作者简介:一名云计算网络运维人员、每天分享网络与运维的技术与干货。 座右铭:低头赶路,敬事如仪 个人主页:网络豆的主页 目录 写在前面 上章回顾 本章简介 本章目标 一.云计算产生背景 1.信息时代的重点变革…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

LangChain【6】之输出解析器:结构化LLM响应的关键工具
文章目录 一 LangChain输出解析器概述1.1 什么是输出解析器?1.2 主要功能与工作原理1.3 常用解析器类型 二 主要输出解析器类型2.1 Pydantic/Json输出解析器2.2 结构化输出解析器2.3 列表解析器2.4 日期解析器2.5 Json输出解析器2.6 xml输出解析器 三 高级使用技巧3…...

Appium下载安装配置保姆教程(图文详解)
目录 一、Appium软件介绍 1.特点 2.工作原理 3.应用场景 二、环境准备 安装 Node.js 安装 Appium 安装 JDK 安装 Android SDK 安装Python及依赖包 三、安装教程 1.Node.js安装 1.1.下载Node 1.2.安装程序 1.3.配置npm仓储和缓存 1.4. 配置环境 1.5.测试Node.j…...
OPENCV图形计算面积、弧长API讲解(1)
一.OPENCV图形面积、弧长计算的API介绍 之前我们已经把图形轮廓的检测、画框等功能讲解了一遍。那今天我们主要结合轮廓检测的API去计算图形的面积,这些面积可以是矩形、圆形等等。图形面积计算和弧长计算常用于车辆识别、桥梁识别等重要功能,常用的API…...
