排序第一课【插入排序】直接插入排序 与 希尔排序
目录
1. 排序的概念:
2.插入排序基本思想
3.直接插入排序
4.希尔排序
1. 排序的概念:
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
2.插入排序基本思想
直接插入排序是一种简单的插入排序法,其基本思想是:
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列。
实际中我们玩扑克牌时,就用了插入排序的思想
3.直接插入排序
直接插入排序(InsertSort),当插入第i(i>=1)个元素时,前面的array[0],array[1]...aray[i-1]已经排好序,此时用array[i]的排序码与array[i-1],array[i-2.]..的排序码顺序进行比较,找到插入位置,即将array[i]插入,原来位置上的元素顺序后移。
直接插入排序图解:
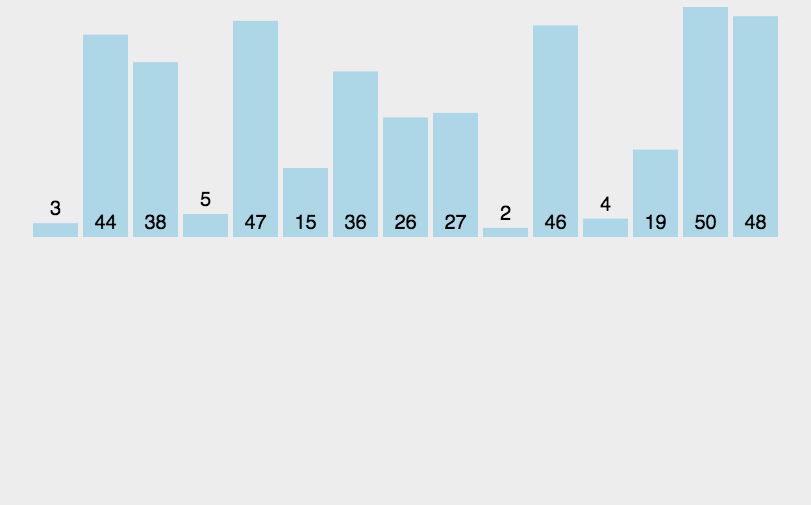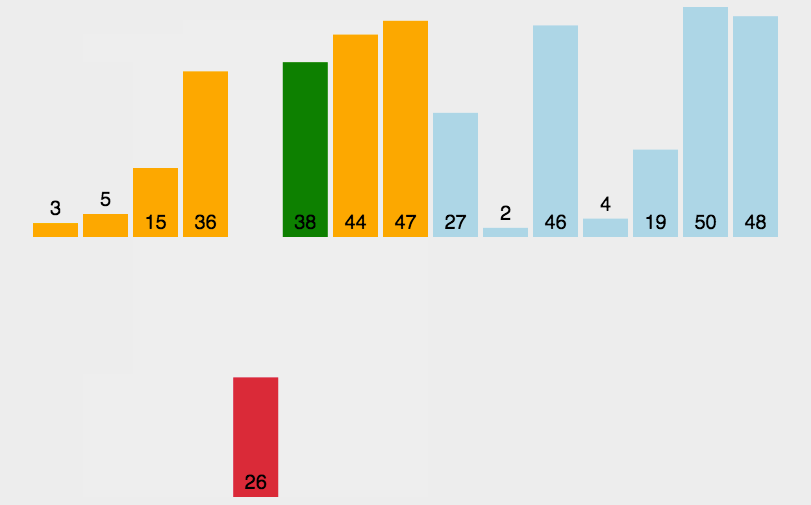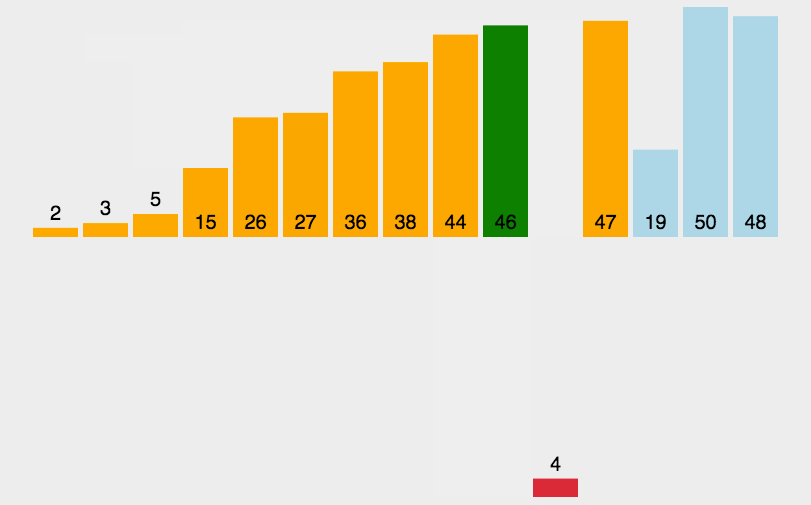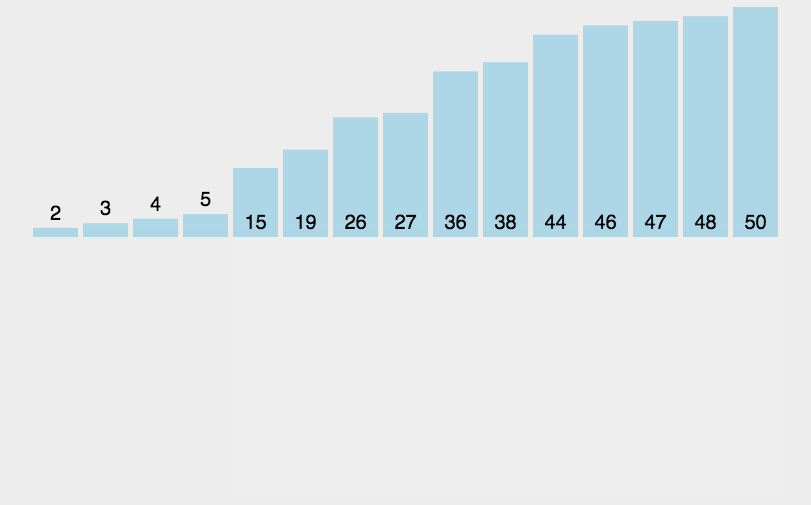
代码实现思路:
假设在数组arr中,[0,end]这段区间是有序的,我们要将 end+1 位置处的元素插入,就需要将arr[end+1]与前面元素从后往前依次作比较,如果要排成升序,前面元素比arr[end+1]大的就往后移动,大或者等于就放在这个元素后面。数组一共有n个元素,要排n-1次,因为第一个元素不用排,从第二个元素开始。
代码:
//直接插入排序 升序
void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int tmp = a[end + 1];while (end >= 0){if (a[end] > tmp){a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = tmp;}
}直接插入排序的特性总结:
- 元素集合越接近有序,直接插入排序算法的时间效率越高
- 时间复杂度:O(N^2)
- 空间复杂度:O(1),它是一种稳定的排序算法
- 稳定性:稳定
4.希尔排序
希尔排序法(ShellSort)又称缩小增量法。希尔排序法的基本思想是:先选定一个整数gap,把待排序文件中所有记录分成gap个组,所有距离为gap的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组和排序的工作。当到达gap==1时,所有记录已经在组内排好序。
- 希尔排序是对直接插入排序的优化,因为直接插入排序处理接近有序的元素集合时,效率会很高,接近O(N)。
- 当gap >1时都是预排序,目的是让数组元素更接近于有序。当gap == 1时,就和直接插入排序相同了,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
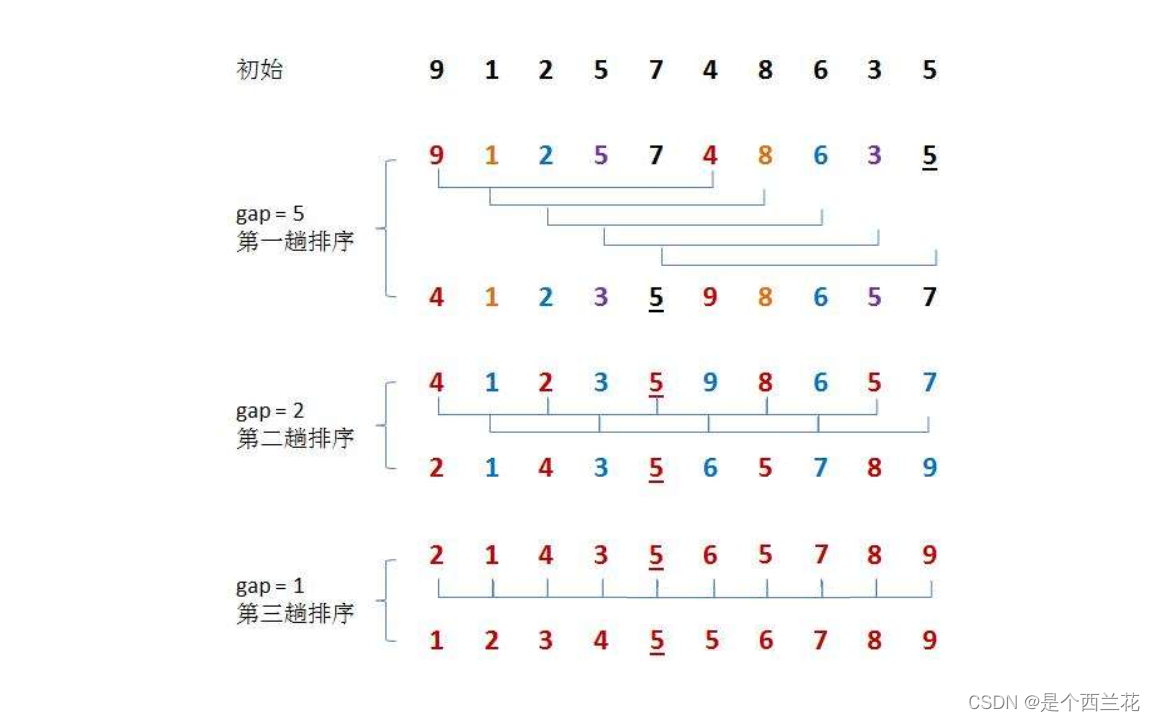
代码实现思路:
我们先要实现预排序,使数组元素集合接近有序。我们先假设gap=3。实现预排序有两种方式,一种是分组排序,排好一组再排下一组,另外一种是多组并排。这两种方法内部还是直接插入排序。大家可以和上面直接插入排序的代码对比一下。
分组排序代码:
//预排序 一组一组预排,
void BeforeSort1(int* arr, int n)
{//假设gap = 3,分为3组,每组n/3个元素int gap = 3;for (int j = 0; j < gap; j++){//每组内部进行排序for (int i = j; i < n - gap; i += gap){int end = i;int tmp = arr[i + gap];while (end >= 0){if (tmp < arr[end]){arr[end + gap] = arr[end];end -= gap;}else{break;}}arr[end + gap] = tmp;}}
}多组并排代码:可以对比一下上面代码。
//预排序 多组并排
void BeforeSort2(int* arr, int n)
{//假设gap = 3,分为3组,每组n/3个元素int gap = 3;for (int i = 0; i < n - gap; i++){int end = i;int tmp = arr[i + gap];while (end >= 0){if (tmp < arr[end]){arr[end + gap] = arr[end];end -= gap;}else{break;}}arr[end + gap] = tmp;}}其实:预处理不是简单的只处理一次,而是处理多次,让数据更加接近有序。最开始gap最大,之后gap每次逐渐减小,直至gap==1。
- gap越大,大的数可以更快的到后面,小的数可以更快的到前面,数据越不接近有序
- gap越小,大的小的数据挪动越慢,但是他越接近有序
- gap == 1,就是直接插入排序
我们这里让gap=n 每次预排让 gap = gap/3+1,确保最后可以得到1。
希尔排序代码实现:对于gap的取法我们下面会讲到。
// 希尔排序 升序
void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1;for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while (end >= 0){if (a[end] > tmp){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}关系希尔排序的时间复杂度以及gap的取法问题:
资料中是这样讲的:
《数据结构(C语言版)》--- 严蔚敏 《数据结构-用面相对象方法与C++描述》--- 殷人昆
《数据结构-用面相对象方法与C++描述》--- 殷人昆

因为我们这里使用的gap是按照Knuth提出的方式取值的,而且Knuth进行了大量的试验统计,我们暂时时间复杂度就按照:O(N^1.25)到O(1.6 * N^1.25)来算。
稳定性:不稳定。
本篇结束!
相关文章:

排序第一课【插入排序】直接插入排序 与 希尔排序
目录 1. 排序的概念: 2.插入排序基本思想 3.直接插入排序 4.希尔排序 1. 排序的概念: 排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。 稳定性…...
云计算——ACA学习 云计算概述
作者简介:一名云计算网络运维人员、每天分享网络与运维的技术与干货。 座右铭:低头赶路,敬事如仪 个人主页:网络豆的主页 目录 写在前面 上章回顾 本章简介 本章目标 一.云计算产生背景 1.信息时代的重点变革…...
如何为网站进行全面的整站翻译?
要翻译整个网站,可以按照以下步骤进行: 确定翻译需求:确定你需要将整个网站翻译成哪种语言。这可以根据你的目标受众和市场进行决定。 寻找翻译资源:你可以选择以下几种方式来进行网站翻译: a. 人工翻译:雇…...

项目部署(前后端分离)
1、前端项目 (打包成dist文件,放到nginx的html目录下面),然后配置nginx 2、后端项目部署 使用之前的shell脚本(然后赋予用户权限),最后运行脚本 查看进程...

增强型Web安全网关在银行的应用
销售,绝不是降低身份去取悦客户,而是像朋友一样给予合理的建议。你刚好需要,我刚好专业!仅此而已! 乔.吉拉德 健康的安全体系,还可以更完善 浙江某商业银行股份有限公司是一家成立多年的商业银行…...

Oracle-ORA-00600:[ktspffbmb:objdchk_kcbnew_3]
问题背景: 应用执行存储过程报错ORA-00600: 内部错误代码, 参数: [ktspffbmb:objdchk_kcbnew_3], [0], [3303775], [4], [], [], [], [], [], [], [], [],导致过程无法正常执行 ORA-00600: 内部错误代码, 参数: [ktspffbmb:objdchk_kcbnew_3], [0], [3303775], [4]…...

SPINN:基于设备和云的神经网络协同递进推理
SPINN:基于设备和云的神经网络协同递进推理 论文标题:SPINN: synergistic progressive inference of neural networks over device and cloud 原文链接:https://dl.acm.org/doi/10.1145/3372224.3419194 论文动机 现代CNN过多的计算需求&am…...

数据结构-二叉树
数据结构-二叉树 二叉树的概念二叉树的遍历分类 建立二叉树,并遍历二叉树的最小单元二叉树的最小单元初始化初始化二叉树前序遍历的实现中序遍历的实现后序遍历的实现计算节点的个数计算树的深度求第k层的个数查找二叉树的元素分层遍历 全部代码如下 二叉树的概念 二…...

Open3D 进阶(4)高斯混合点云聚类
目录 一、算法原理1、原理概述2、实现流程3、参考文献二、代码实现三、结果展示四、测试数据本文由CSDN点云侠原创,原文链接。爬虫网站自重。 一、算法原理 1、原理概述 高斯混合聚类(GMM)算法假设数据点是由一个或多个高斯分布生成的,并通过最大似然估计的方法来估计每个簇…...

计算机组成和IO
文章目录 计组和Epoll:计算机组成原理:网络数据接收的流程:内核如何管理socket以及状态的更新select系统调用的复杂度epoll的et和lt模式及java的选择 国内访问chatai就可以 https://aiweb.douguguo.com/?typeadd计组和Epoll: 计…...
STM32CUBUMX配置RS485 modbus STM32(从机)亲测可用
———————————————————————————————————— ⏩ 大家好哇!我是小光,嵌入式爱好者,一个想要成为系统架构师的大三学生。 ⏩最近在开发一个STM32H723ZGT6的板子,使用STM32CUBEMX做了很多驱动&#x…...

系统设计类题目汇总
1 设计一个系统统计当前时刻北京用户在线人数 【Redis】位图以及位图的使用场景(统计在线人数和用户在线状态) 1.1 方案一: 在用户登录时,使用 Redis SET 将用户 ID 添加到一个特定的键(例如 “online:beijing”)。用户退出时&…...

css滚动条样式指南
css滚动条样式指南 滚动条是网页设计中经常被忽视的元素。虽然它看起来像是一个小细节,但它在网站导航中起着至关重要的作用。默认的滚动条可能看起来不合适,有损整体美观。本文将介绍如何使用 CSS 自定义滚动条。 在 Chrome、Edge 和 Safari 中设置滚…...
)
vue子组件修改父组件传递的变量(自定义日期时间组件,时间间隔为15分钟或者一个小时)
vue子组件修改父组件传递的变量 子组件不能直接修改父组件变量的值,但是可以通过调用父组件的方法来修改。 实现步骤 在父组件声明变量 export default {data() {return {startTime:"",......},......} }在父组件使用子组件并传递数据,修改…...

【PyTorch】nn.Conv2d函数详解
nn.Conv2d 是 PyTorch 中的一个卷积层,用于实现二维卷积操作 torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride1, padding0, dilation1, groups1, biasTrue, padding_modezeros, deviceNone, dtypeNone )参数解释 in_channels:输入的通…...

数智保险 创新未来 | GBASE南大通用亮相中国保险科技应用高峰论坛
本届峰会以“数智保险 创新未来”为主题,GBASE南大通用携新一代创新数据库产品及金融信创解决方案精彩亮相,与国内八百多位保险公司高管和众多保险科技公司技术专家,就保险领域数字化的创新应用及生态建设、新一代技术突破及发展机遇、前沿科…...

分布式天梯图算法在 Redis 图数据库中的应用
分布式天梯图算法在 Redis 图数据库中的应用 一、简介1 天梯图算法2 天梯图算法在Redis的应用 二、Redis分布式天梯图算法设计与优化1 基于天梯图的分布式算法设计2 多节点扩展与负载均衡优化3 数据存储方案与压缩策略 三、技术实现3.1 系统架构设计3.2 技术选型3.3 关键实现细…...
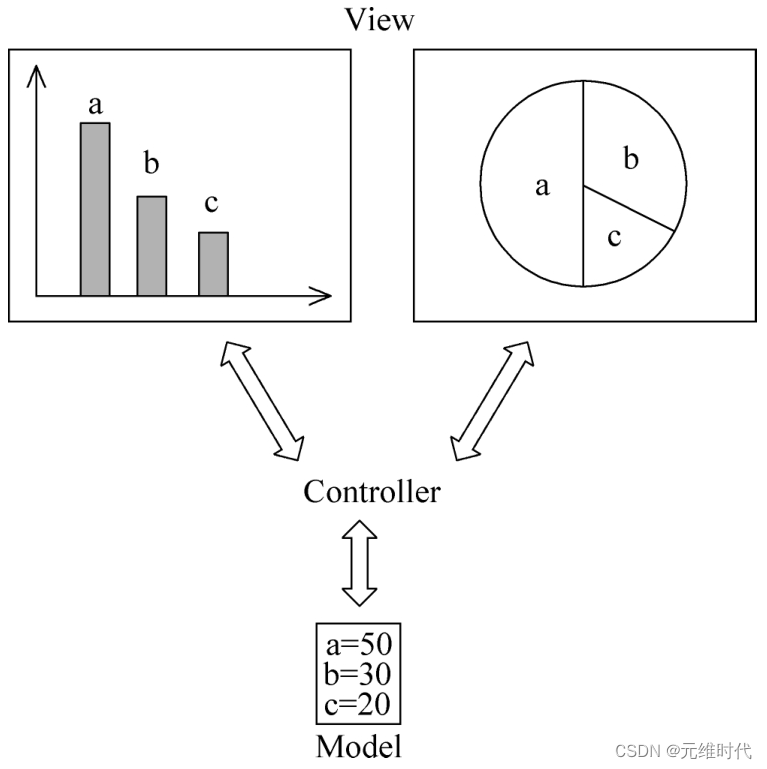
观察者模式——对象间的联动
1、简介 1.1、概述 在软件系统中,有些对象之间也存在类似交通信号灯和汽车之间的关系。一个对象的状态或行为的变化将导致其他对象的状态或行为也发生改变,它们之间将产生联动,正所谓“触一而牵百发”。为了更好地描述对象之间存在的这种一…...

【雕爷学编程】Arduino动手做(189)---特别苗条,使用微波传感器控制的纤细小车
装修屋子,找了一段墙面布线槽,外槽宽度只有23毫米,截取一段长为24厘米,尝试做个苗条小车 先在线槽上安装了二只N20小电机 装上二个快餐盒盖做轮子 测试一下使用3.7V锂电池的动力系统(视频) https://v.youk…...

机器学习基础算法及其实现
线性回归 知识点: 1. 线性回归模型可以使用不同的目标函数,最常用的是最小二乘法、最小绝对值法和最大似然法。 2. 在最小二乘法中,目标是最小化实际值与预测值之间的误差平方和,这可以通过求导数等方法来求解。 3. 在最小绝对值…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

Cursor AI 账号纯净度维护与高效注册指南
Cursor AI 账号纯净度维护与高效注册指南:解决限制问题的实战方案 风车无限免费邮箱系统网页端使用说明|快速获取邮箱|cursor|windsurf|augment 问题背景 在成功解决 Cursor 环境配置问题后,许多开发者仍面临账号纯净度不足导致的限制问题。无论使用 16…...

Angular中Webpack与ngx-build-plus 浅学
Webpack 在 Angular 中的概念 Webpack 是一个模块打包工具,用于将多个模块和资源打包成一个或多个文件。在 Angular 项目中,Webpack 负责将 TypeScript、HTML、CSS 等文件打包成浏览器可以理解的 JavaScript 文件。Angular CLI 默认使用 Webpack 进行项目…...
生成对抗网络(GAN)损失函数解读
GAN损失函数的形式: 以下是对每个部分的解读: 1. , :这个部分表示生成器(Generator)G的目标是最小化损失函数。 :判别器(Discriminator)D的目标是最大化损失函数。 GAN的训…...
