不平衡电网条件下基于变频器DG操作的多目标优化研究(Matlab代码Simulink实现)
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码&Simulink实现&文章讲解
💥1 概述
文献来源:

最近,利用并网转换器(GCC)克服电网故障并支撑电网电压已成为电网规范中反映的主要要求。本文提出了一种新颖的参考电流产生方案,该方案通过使用四个控制参数注入一组适当的正/负有功/无功电流来支持电网电压。提出了解析表达式以获得这些参数在任何电网电压条件下的最优值。通过实现以下目标,可以获得最佳性能:第一,符合相电压限制,第二,最大化有功和无功功率输出,第三,最小化故障电流,第四,减少有功和无功功率的振荡。这些最佳行为为新兴的GCC带来了显著的优势,例如提高效率,降低直流母线纹波,提高交流系统稳定性以及避免设备跳闸。仿真和实验结果验证了分析结果和所提表达式的有效性。
可再生能源和分布式发电(DG)机组在电力中的渗透率越来越高 系统造成了严重的稳定性问题。因此,系统规划人员一直在制定严格的 异常电网条件下并网转换器 (GCC) 运行的要求 [1]–[3]。因此,海湾合作委员会 不仅应承受此类干扰并继续为电网供电,还应提供电压/频率支持。 GCC是否符合这些新要求已在文献中进行了广泛的研究,例如, 在[1]–[20]中。在此 关于GCCs的许多控制策略已经在[13]-[20]中提出。
本文使用最先进的参考电流发生器(RCG)策略(在[3]中介绍),可以灵活地包含正/负和有功/无功 电流。该RCG通过两个控制参数提供有价值的电压支持服务,kp和kq ,在相应有源和 无功电流。同样,有功和无功功率(P和Q)的参考值可以被视为其他两个参考值。**



📚2 运行结果

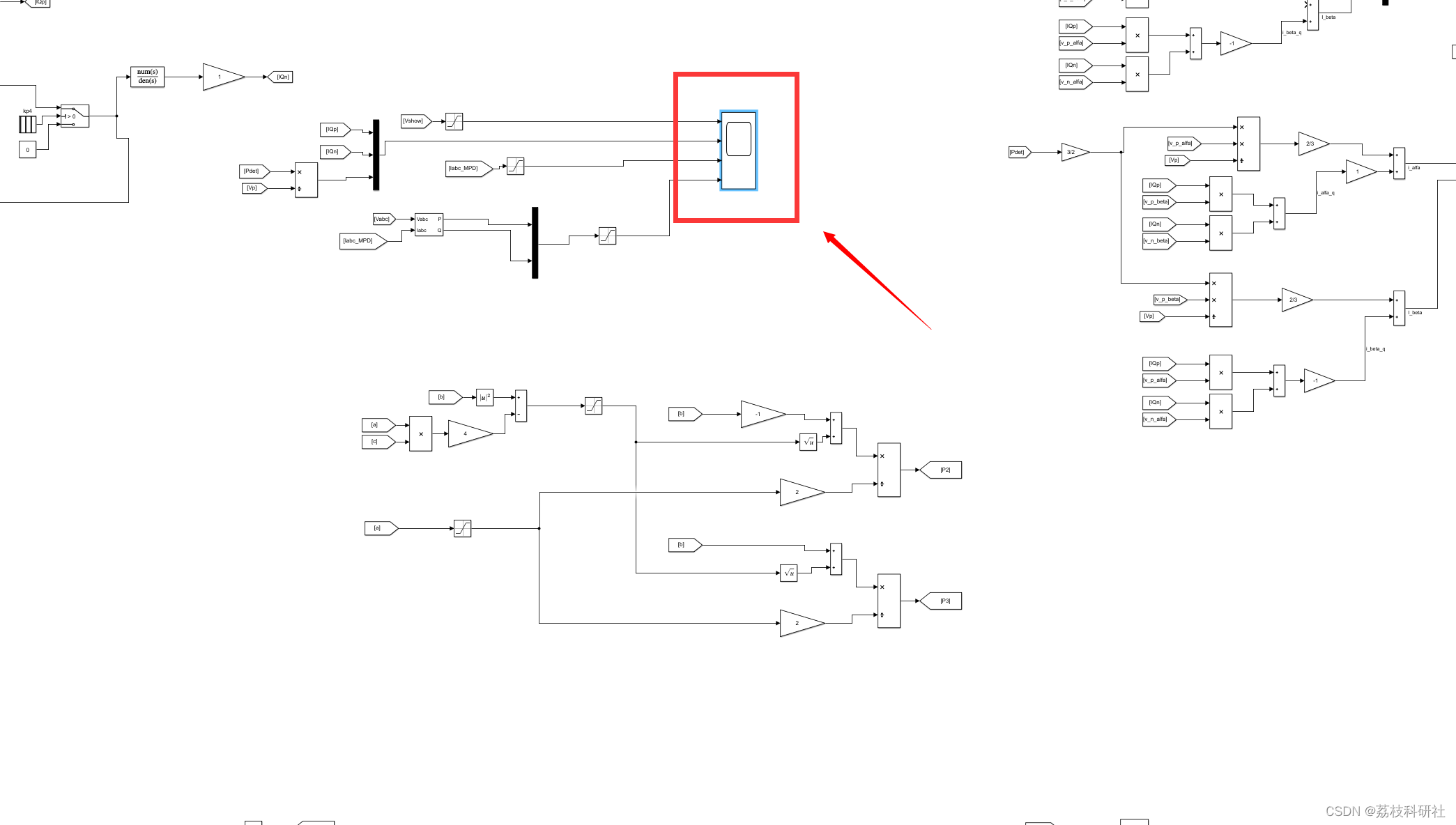



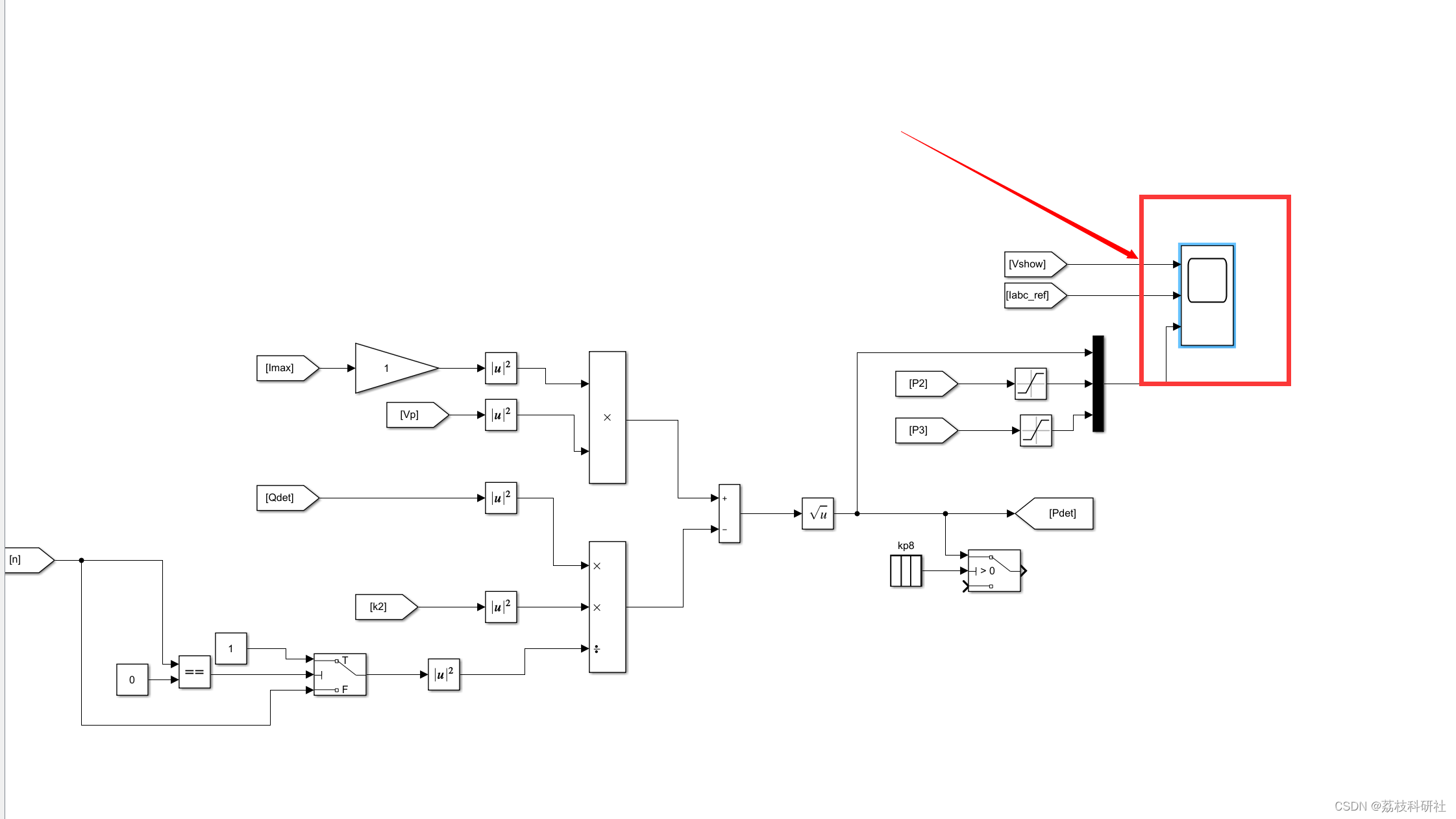


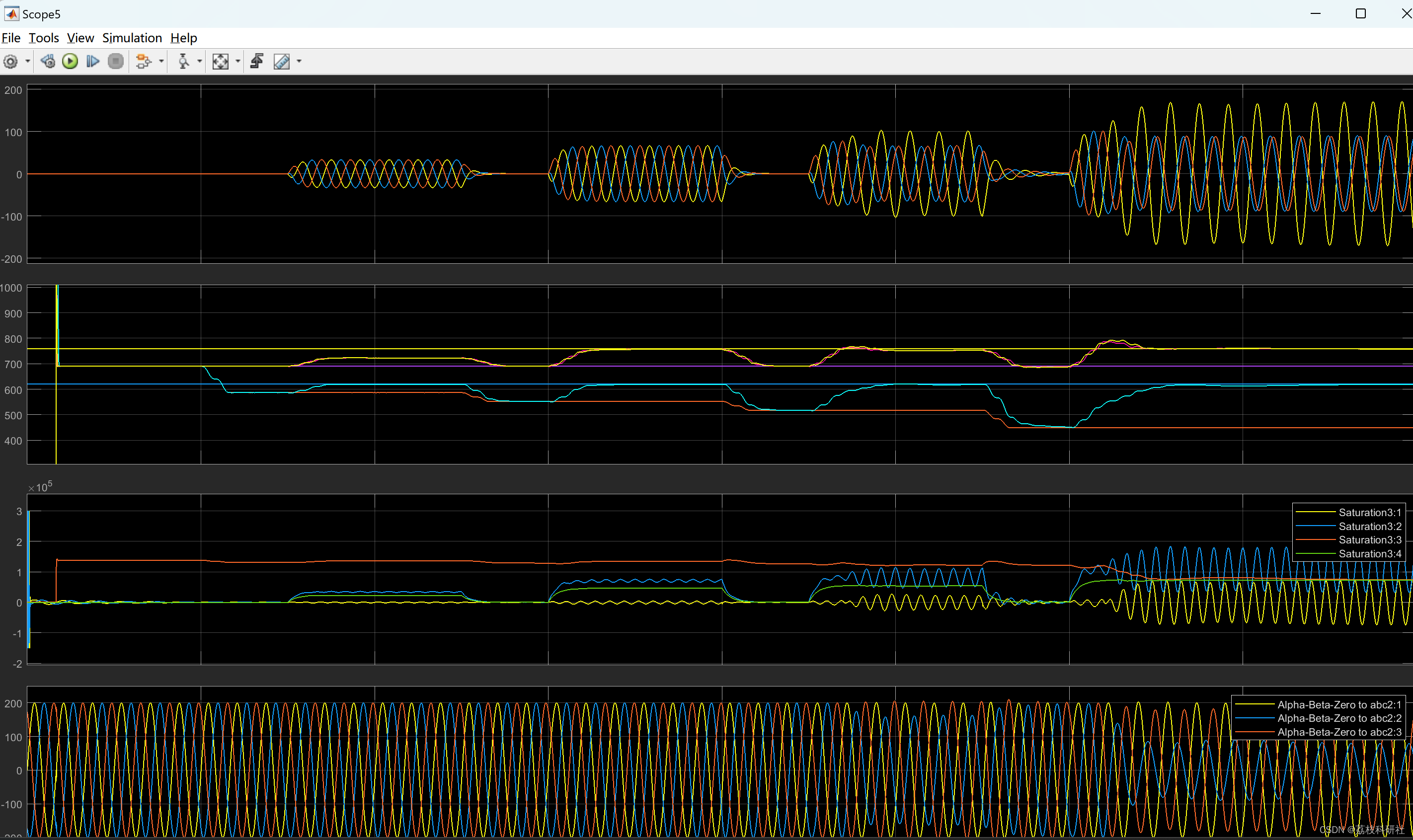

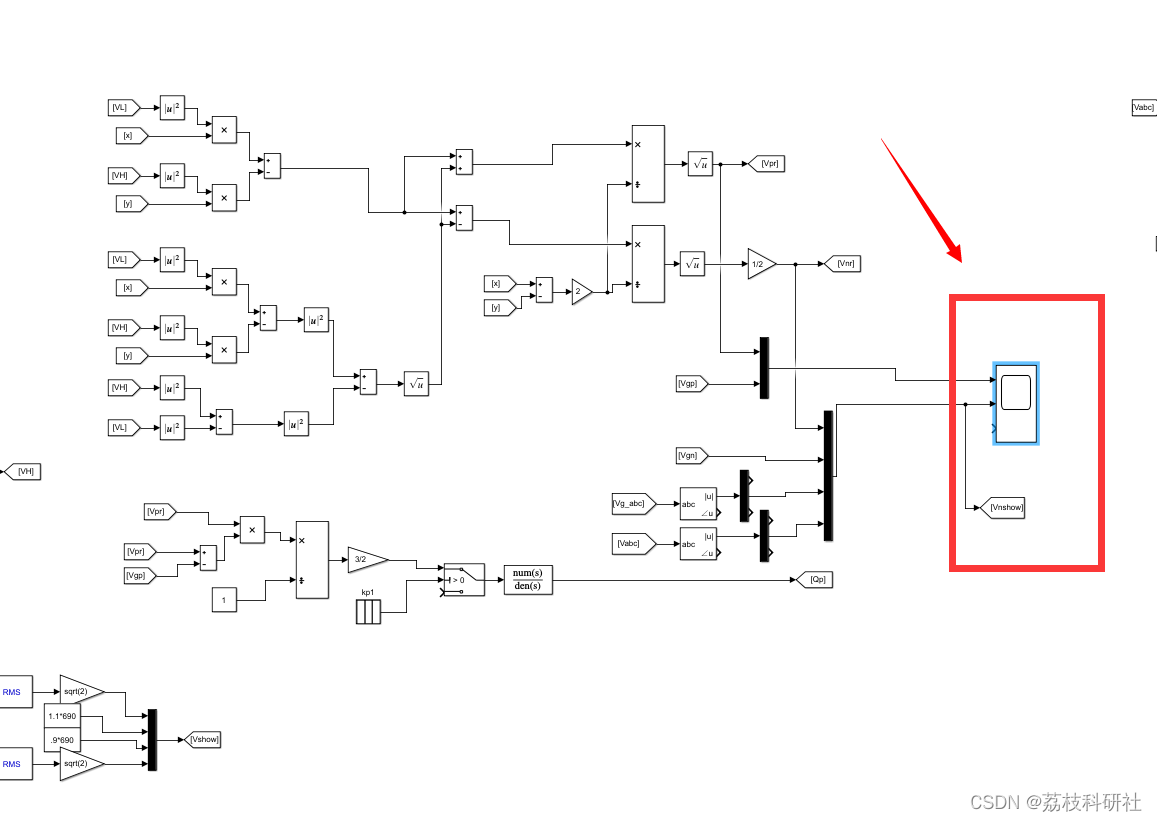

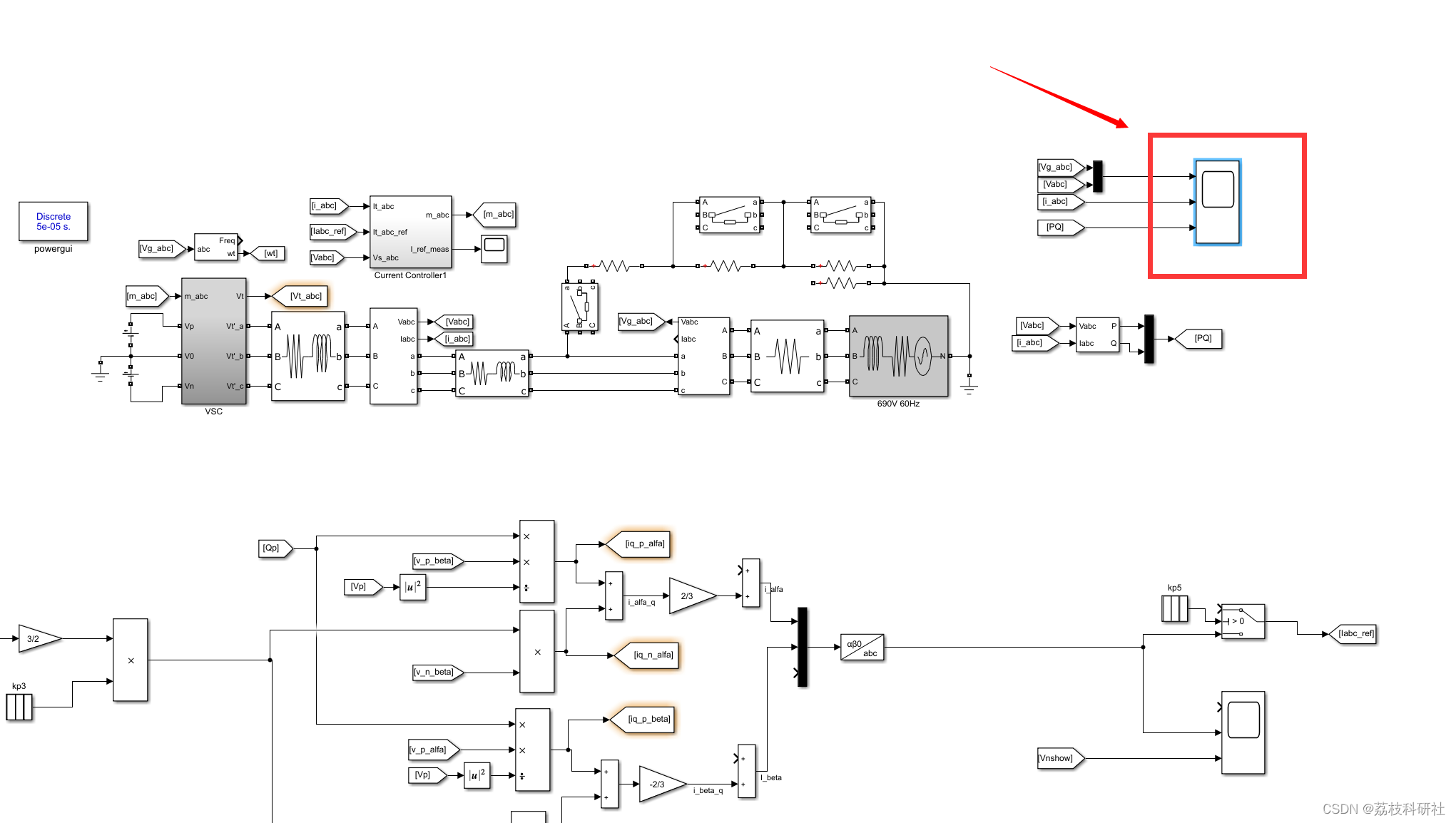
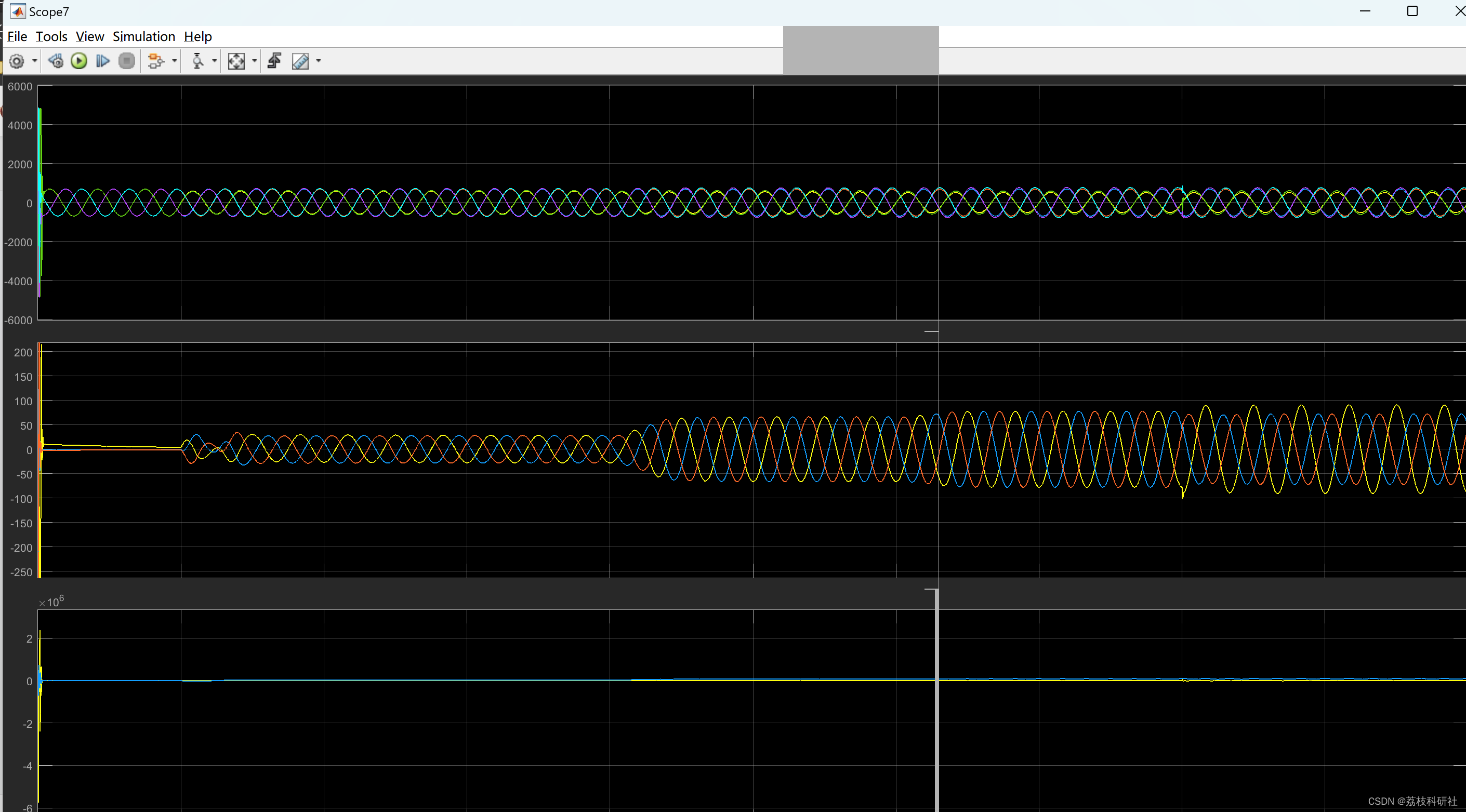

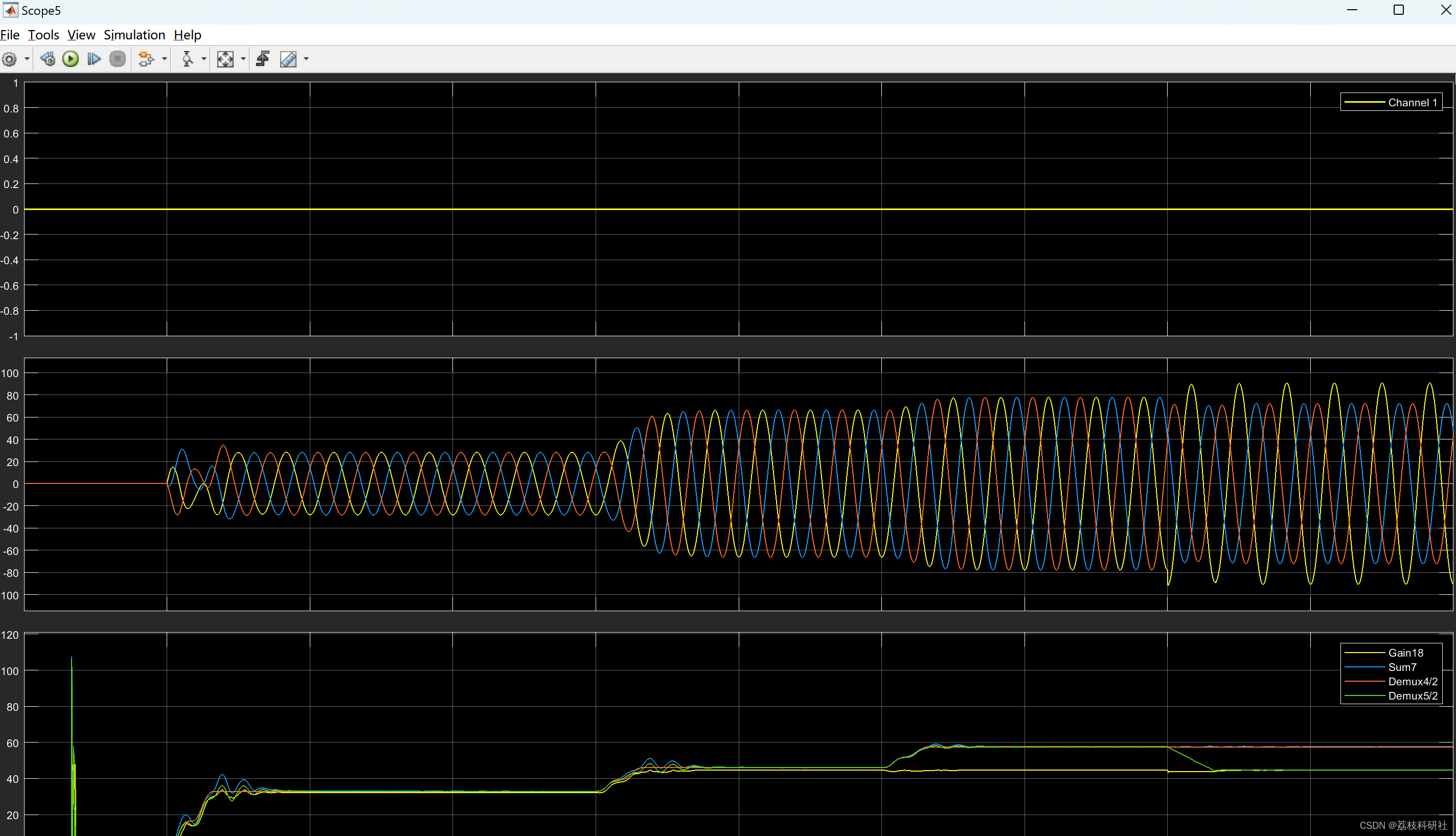

 所有模型和讲解见第4部分。
所有模型和讲解见第4部分。
set(0,'DefaultAxesFontSize',24,'DefaultAxesFontName','Helvetica','DefaultAxesFontWeight','bold','DefaultLineLineWidth',2,'DefaultAxesLineWidth',1)
plot(k1,Imax,'--','color',[0 .45 .74],'LineWidth',6)
grid on
hold on
plot(k1,sqrt(Ia),'color',[0.75 0 .75])
plot(k1,sqrt(Ib),'color',[.85 .33 .1])
plot(k1,sqrt(Ic),'color',[0 .5 0])
legend('Imax','Ia','Ib','Ic')
hold on
plot(k1_opt(O),min(Imax_opt),'s','color',[0 .45 .74],'MarkerSize',25,'MarkerFaceColor',[0 .45 .74])
plot(k1(J),min(Imax),'o','color',[.85 .33 .1],'LineWidth',2,'MarkerSize',15)
title(['P=', num2str(P(p)), ' pu Q=', num2str(Q(q)), ' pu Vp=', num2str(Vp(vp)), ' pu Vn=', num2str(Vn(vn)), ' pu k_q=', num2str(k2(k)),' pu k_p_,_o_p_t= ', num2str(k1_opt(O(1))), ' I_m_a_x_,_o_p_t= ', num2str(min(Imax_opt)), ' pu'])
xlabel('k_p');
ylabel('I_m_a_x (pu)');
%%
A=3*P(p)^2*n; B=-3*P(p)^2*n+sqrt(3)*P(p)*Q(q)*n*(2*k2(k)-1); C=3*n*k2(k)*Q(q)^2*(1-k2(k))-sqrt(3)*P(p)*Q(q)*n*k2(k);
delta=B^2-4*A*C;
if delta>=0
k1_intsec_IaIb=(-B+sqrt(delta))/2/A;
o_num=4;
k1_opt(o_num)=k1_intsec_IaIb;
if k1_intsec_IaIb<1 && k1_intsec_IaIb>0
K1_intsec=P(p)/Vn(vn)*((n+1)*k1_intsec_IaIb-1);
K2_intsec=Q(q)/Vn(vn)*((n-1)*k2(k)+1);
K3_intsec=P(p)/Vn(vn)*((n-1)*k1_intsec_IaIb+1);
K4_intsec=Q(q)/Vn(vn)*((n+1)*k2(k)-1);
Ia_intsec=K1_intsec^2+K2_intsec^2;
Ic_intsec=(-.5*K1_intsec-sqrt(3)/2*K4_intsec)^2+(.5*K2_intsec-sqrt(3)/2*K3_intsec)^2;
plot(k1_intsec_IaIb,sqrt(Ia_intsec),'s','color',[0 .45 .74],'MarkerSize',25)
Imax_intsec=sqrt(max(Ia_intsec,Ic_intsec));
end
end
%%
A=3*P(p)^2*n; B=-3*P(p)^2*n-sqrt(3)*P(p)*Q(q)*n*(2*k2(k)-1); C=3*n*k2(k)*Q(q)^2*(1-k2(k))+sqrt(3)*P(p)*Q(q)*n*k2(k);
delta_IaIc=B^2-4*A*C;
if delta_IaIc>=0
k1_intsec_IaIc=(-B+sqrt(delta_IaIc))/2/A;
if k1_intsec_IaIc<1 && k1_intsec_IaIc>0
K1_intsec=P(p)/Vn(vn)*((n+1)*k1_intsec_IaIc-1);
K2_intsec=Q(q)/Vn(vn)*((n-1)*k2(k)+1);
K3_intsec=P(p)/Vn(vn)*((n-1)*k1_intsec_IaIc+1);
K4_intsec=Q(q)/Vn(vn)*((n+1)*k2(k)-1);
Ia_intsec=K1_intsec^2+K2_intsec^2;
Ib_intsec=(-.5*K1_intsec+sqrt(3)/2*K4_intsec)^2+(.5*K2_intsec+sqrt(3)/2*K3_intsec)^2;
plot(k1_intsec_IaIc,sqrt(Ia_intsec),'s','color',[0 .45 .74],'MarkerSize',25)
end
end
end
i=i+1;
end
end
end
end
% end
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]M. M. Shabestary and Y. A. -R. I. Mohamed, "Analytical Expressions for Multiobjective Optimization of Converter-Based DG Operation Under Unbalanced Grid Conditions," in IEEE Transactions on Power Electronics, vol. 32, no. 9, pp. 7284-7296, Sept. 2017, doi: 10.1109/TPEL.2016.2628405.
[2]谭畅舒,李艳,田杰,明威宇,李妍,王少荣.计及分布式能源的主动配电网恢复力综合评估[J].电力科学与技术学报,2023,38(01):108-113.DOI:10.19781/j.issn.1673-9140.2023.01.012.
[3]葛钦. 电网故障下电力电子变压器故障穿越机理与控制策略研究[D].湖南大学,2020.DOI:10.27135/d.cnki.ghudu.2020.000151.
[4]庞永恒. 基于故障失配度的含新能源配电网接地故障定位方法研究[D].东北大学,2017.
🌈4 Matlab代码&Simulink实现&文章讲解
相关文章:

不平衡电网条件下基于变频器DG操作的多目标优化研究(Matlab代码Simulink实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 🌈4 Matlab代码&Simulink实现&文章讲解 💥1 概述 文献来源: 最近,利用并网转换器(GCC)克服电网故障并支撑电网电压已…...
简单题||单词数)
【Leetcode】(自食用)简单题||单词数
step by step. 题目: 统计字符串中的单词个数,这里的单词指的是连续的不是空格的字符。 请注意,你可以假定字符串里不包括任何不可打印的字符。 示例: 输入: "Hello, my name is John" 输出: 5 解释: 这里的单词是指连续的不是空格…...

C语言代码的x86-64汇编指令分析过程记录
先通过Xcode创建一个terminal APP,语言选择C。代码如下: #include <stdio.h>int main(int argc, const char * argv[]) {int a[7]{1,2,3,4,5,6,7};int *ptr (int*)(&a1);printf("%d\n",*(ptr));return 0; } 在return 0处打上断点&…...
基于springboot+vue的房屋租赁系统(前后端分离)
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战 主要内容:毕业设计(Javaweb项目|小程序等)、简历模板、学习资料、面试题库、技术咨询 文末联系获取 项目介绍…...

Python文件读写操作详解:从基础到高级
摘要:文件读写是Python编程中常见的操作之一。本文将介绍Python中文件读写的基础知识,包括打开文件、读取文件内容、写入文件、关闭文件等基本操作。此外,还将探讨一些高级文件读写技术,如使用上下文管理器、处理异常、使用with语…...
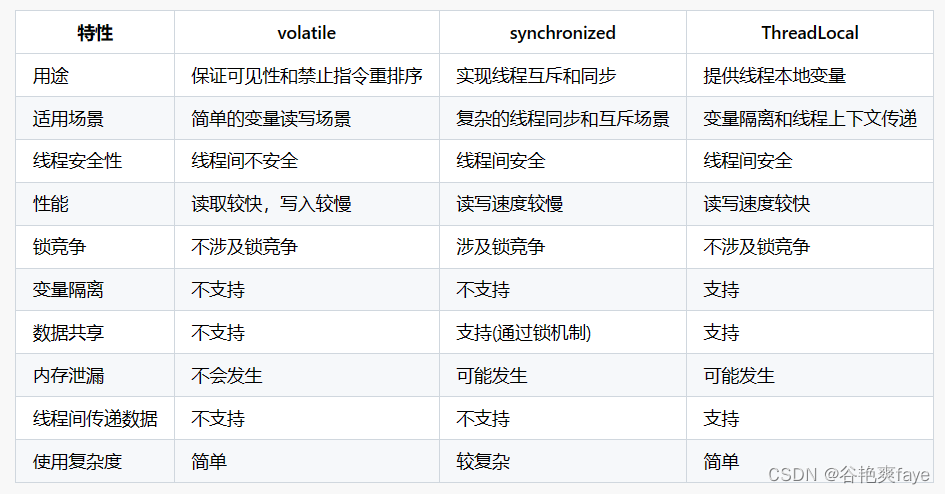
ThreadLocal基本介绍
文章目录 什么是ThreadLocalThreadLocal解决了什么问题ThreadLocal的作用 ThreadLocal的使用场景ThreadLocal的代码示例ThreadLocal的优点ThreadLocal的缺点与volatile、synchronized、ThreadLocal比较 总结 什么是ThreadLocal ThreadLocal是Java中的一个线程本地变量…...
ffmpeg源码编译成功,但是引用生成的静态库(.a)报错,报错位置在xxx_list.c,报错信息为某变量未定义
背景:本文是对上一个文章的补充,在源码编译之前,项目是有完整的ffmpeg编译脚本的,只不过新增了断点调试ffmpeg,所以产生的上面的文章,也就是说,我在用make编译成功后,再去做的源码编…...

2023爱分析·信创云市场厂商评估报告:中国电子云
01 研究范围定义 信创2.0时代开启,信创进程正在从局部到全面、从细分到所有领域延展。在这个过程中,传统的系统集成,也在逐步向信创化、数字化及智能化转变。随着信创产业的发展,企业需要更多的技术支持和服务,而传统的系统集成已…...

网络安全学习笔记——XFF攻击流程
手工注入 手动报错注入,填写格式如:X-Forwarded-For: and updatexml(1,concat(0x7e,(select database()),0x7e),1) or 11 库名 1 and updatexml(1,concat(0x7e,database(),0x7e),1), 表名 1 and updatexml(1,concat(0x7e,(select table_name from…...

微信小程序阻止用户返回上一页,并弹窗给用户确定是否要返回上一页
在onload中调用微信的enableAlertBeforeUnload方法,在首次进入会自动监听当前的页面,在返回的时候会自动弹出弹窗阻止用户返回上一页,点击确定则返回上一页,取消则停留在当前页 onLoad: function(){wx.enableAlertBeforeUnload({…...
LangChain+ChatGLM整合LLaMa模型(二)
开源大模型语言LLaMa LLaMa模型GitHub地址添加LLaMa模型配置启用LLaMa模型 LangChainChatGLM大模型应用落地实践(一) LLaMa模型GitHub地址 git lfs clone https://huggingface.co/huggyllama/llama-7b添加LLaMa模型配置 在Langchain-ChatGLM/configs/m…...
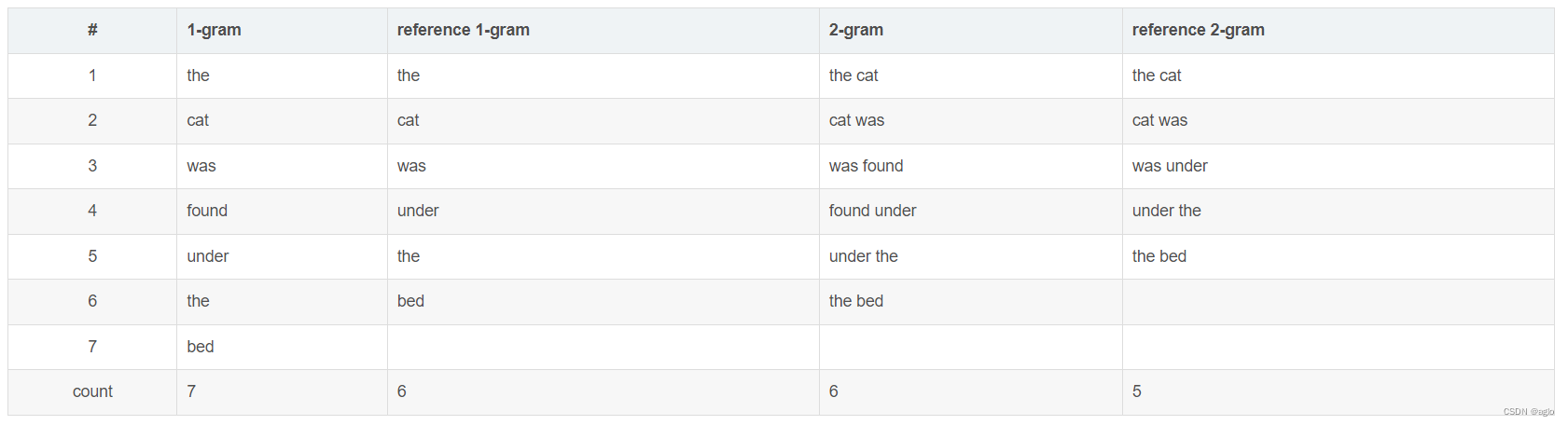
【NLP】训练chatglm2的评价指标BLEU,ROUGE
当进行一定程度的微调后,要评价模型输出的语句的准确性。由于衡量的对象是一个个的自然语言文本,所以通常会选择自然语言处理领域的相关评价指标。这些指标原先都是用来度量机器翻译结果质量的,并且被证明可以很好的反映待评测语句的准确性&a…...

java+springboot+mysql员工工资管理系统
项目介绍: 使用javaspringbootmysql开发的员工工资管理系统,系统包含超级管理员,系统管理员、员工角色,功能如下: 超级管理员:管理员管理;部门管理;员工管理;奖惩管理&…...
FL Studio Producer Edition 21 v21.0.3 Build 3517 Windows/mac官方中文版
FL Studio Producer Edition 21 v21.0.3 Build 3517 Windows FL Studio Producer Edition 21 v21.0.3 Build 3517 Windows/mac官方中文版是一个完整的软件音乐制作环境或数字音频工作站(DAW)。它代表了 25 多年的创新发展,将您创作、编曲、录…...

探索Python数据容器之乐趣:列表与元组的奇妙旅程!
文章目录 零 数据容器入门一 数据容器:list(列表)1.1 列表的定义1.2 列表的下表索引1.3 列表的常用操作1.3.1 列表的查询功能1.3.2 列表的修改功能1.3.3 列表常用方法总结 1.4 补充:append与extend对比1.5 list(列表)的遍历1.6 补…...
Python自动化实战之使用Pytest进行API测试详解
概要 每次手动测试API都需要重复输入相同的数据,而且还需要跑多个测试用例,十分繁琐和无聊。那么,有没有一种方法可以让你更高效地测试API呢?Pytest自动化测试!今天,小编将向你介绍如何使用Pytest进行API自…...
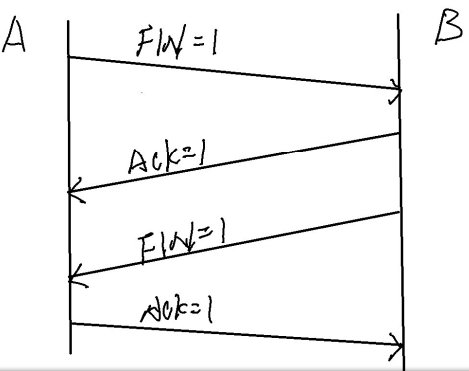
TCP的三次握手以及四次断开
TCP的三次握手和四次断开,就是TCP通信建立连接以及断开的过程 目录 【1】TCP的三次握手过程 ---- TCP建立连接的过程 【2】TCP的四次挥手 ---- TCP会话的断开 注意: 【1】TCP的三次握手过程 ---- TCP建立连接的过程 三次握手的过程:…...

目标检测YOLO实战应用案例100讲-基于视觉与激光雷达信息融合的智能车辆目标检测研究
目录 前言 传感器选型及同步 2.1 各传感器工作原理及性能对比 2.1.1 视觉传感器...

Day 22 C++ STL常用容器——string容器
string容器 概念本质string和char 区别:特点string构造函数构造函数原型 string赋值操作赋值的函数原型示例 string字符串拼接函数原型:示例 string查找和替换函数原型示例 string字符串比较比较方式 字符串比较是按字符的ASCII码进行对比函数原型示例 s…...

使用Socket实现UDP版的回显服务器
文章目录 1. Socket简介2. DatagramSocket3. DatagramPacket4. InetSocketAddress5. 实现UDP版的回显服务器 1. Socket简介 Socket(Java套接字)是Java编程语言提供的一组类和接口,用于实现网络通信。它基于Socket编程接口,提供了…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...

