P1629 邮递员送信(最短路)(内附封面)
邮递员送信
题目描述
有一个邮递员要送东西,邮局在节点 1 1 1。他总共要送 n − 1 n-1 n−1 样东西,其目的地分别是节点 2 2 2 到节点 n n n。由于这个城市的交通比较繁忙,因此所有的道路都是单行的,共有 m m m 条道路。这个邮递员每次只能带一样东西,并且运送每件物品过后必须返回邮局。求送完这 n − 1 n-1 n−1 样东西并且最终回到邮局最少需要的时间。
输入格式
第一行包括两个整数, n n n 和 m m m,表示城市的节点数量和道路数量。
第二行到第 ( m + 1 ) (m+1) (m+1) 行,每行三个整数, u , v , w u,v,w u,v,w,表示从 u u u 到 v v v 有一条通过时间为 w w w 的道路。
输出格式
输出仅一行,包含一个整数,为最少需要的时间。
样例 #1
样例输入 #1
5 10
2 3 5
1 5 5
3 5 6
1 2 8
1 3 8
5 3 4
4 1 8
4 5 3
3 5 6
5 4 2
样例输出 #1
83
提示
对于 30 % 30\% 30% 的数据, 1 ≤ n ≤ 200 1 \leq n \leq 200 1≤n≤200。
对于 100 % 100\% 100% 的数据, 1 ≤ n ≤ 1 0 3 1 \leq n \leq 10^3 1≤n≤103, 1 ≤ m ≤ 1 0 5 1 \leq m \leq 10^5 1≤m≤105, 1 ≤ u , v ≤ n 1\leq u,v \leq n 1≤u,v≤n, 1 ≤ w ≤ 1 0 4 1 \leq w \leq 10^4 1≤w≤104,输入保证任意两点都能互相到达。
F l o y d Floyd Floyd 逃课做法(要开O2)
直接套 F l o y d Floyd Floyd
最后的结果是每个点到 1 节点的距离与 1 到每个点的距离之和,注意存储初始距离时保留最短的一条,否则会WA
F l o y d Floyd Floyd做法代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e3+111;
int n,m,ans=0;
int dis[N][N];
int main(){cin>>n>>m;memset(dis,0x3f,sizeof(dis));for(int i=1;i<=m;i++){int u,v,w;cin>>u>>v>>w;dis[u][v]=min(dis[u][v],w);//dis[u][v]=w;}for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);}}}for(int i=2;i<=n;i++){ans+=dis[i][1]+dis[1][i];}cout<<ans<<endl;return 0;
}
d i j k s t r a dijkstra dijkstra堆优化
从 1 1 1 跑到其他 2 n 2~n 2 n 节点需要跑一遍 d i j k s t r a dijkstra dijkstra
返回 1 1 1节点也需要跑一遍 d i j k s t r a dijkstra dijkstra
因此我们在 u + n u+n u+n 与 v + n v+n v+n 建一个反图,方便反跑
需要堆优化
答案累加 2 2 2累加到 n n n,反跑后从 2 + n 2+n 2+n 累加到 n ∗ 2 n*2 n∗2即可
AC CODE
#include<bits/stdc++.h>
using namespace std;
const int N=1e4+49999;
int n,m,ans=0;
int dis[N];
vector<pair<int,int> > a[N];
bool vis[N];
void dijkstra(int s){priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > >q;memset(dis,0x3f,sizeof(dis));memset(vis,0,sizeof(vis));dis[s]=0;q.push({0,s});while(!q.empty()){pair<int,int> tmp=q.top();q.pop();int x=tmp.second;int y=tmp.first;if(dis[x]<tmp.first)continue;if(vis[x]==1)continue;vis[x]=1;for(int i=0;i<a[x].size();i++){if(dis[a[x][i].first]>y+a[x][i].second){dis[a[x][i].first]=y+a[x][i].second;q.push({dis[a[x][i].first],a[x][i].first});}}}
}
int main(){cin>>n>>m;for(int i=1;i<=m;i++){int u,v,w;cin>>u>>v>>w;a[u].emplace_back(make_pair(v,w));a[v+n].emplace_back(make_pair(u+n,w));}dijkstra(1);for(int i=2;i<=n;i++){ans+=dis[i];}dijkstra(1+n);for(int i=2+n;i<=n*2;i++){ans+=dis[i];}cout<<ans<<endl;return 0;
}
附封面(碧蓝档案)

相关文章:

P1629 邮递员送信(最短路)(内附封面)
邮递员送信 题目描述 有一个邮递员要送东西,邮局在节点 1 1 1。他总共要送 n − 1 n-1 n−1 样东西,其目的地分别是节点 2 2 2 到节点 n n n。由于这个城市的交通比较繁忙,因此所有的道路都是单行的,共有 m m m 条道路。这…...
网络安全--原型链污染
目录 1.什么是原型链污染 2.原型链三属性 1)prototype 2)constructor 3)__proto__ 4)原型链三属性之间关系 3.JavaScript原型链继承 1)分析 2)总结 3)运行结果 4.原型链污染简单实验 1)实验一 2࿰…...
Harbor企业镜像仓库部署
目录 一、Harbor 架构构成 二、部署harbor环境 1、安装docker-ce(所有主机) 2、阿里云镜像加速器 3、部署Docker Compose 服务 4、部署 Harbor 服务 5、启动并安装 Harbor 6、创建一个新项目 三、客户端上传镜像 1、在 Docker 客户端配置操作如下…...
:分类问题-softmax回归)
【AI】《动手学-深度学习-PyTorch版》笔记(十一):分类问题-softmax回归
AI学习目录汇总 1、线性回归和softmax回归的区别 1)连续值与离散值 线性回归模型,适用于输出为连续值的情景。 softmax回归模型,适用于输出为离散值的情景。例如图像类别,就需要对离散值进行预测。softmax回归模型引入了softmax运算,使输出更适合离散值的预测和训练。 …...
(含代码)(完工于2023.8.3))
【排序算法略解】(十种排序的稳定性,时间复杂度以及实现思想)(含代码)(完工于2023.8.3)
文章目录 1、冒泡排序/选择排序/插入排序冒泡排序(Bubble Sort)选择排序(Selection Sort)插入排序(Insertion Sort) 2、希尔排序(Shells Sort)3、快速排序(Quick Sort)4、堆排序(Heap Sort)5、归并排序(Merge Sort)6、桶排序/计数排序/基数排序桶排序(Bucket sort)计数排序(Cou…...
学编程实用网站
牛客网:面试刷题和面试经验分享的网站牛客网 - 找工作神器|笔试题库|面试经验|实习招聘内推,求职就业一站解决_牛客网 (nowcoder.com)https://www.nowcoder.com/ 慕课网:在线学习 慕课网-程序员的梦工厂 (imooc.com)https://www.imooc.com/ …...

Camunda 7.x 系列【5】 员工请假流程模型
有道无术,术尚可求,有术无道,止于术。 本系列Spring Boot 版本 2.7.9 本系列Camunda 版本 7.19.0 源码地址:https://gitee.com/pearl-organization/camunda-study-demo 文章目录 1. 概述2. 模型设计2.1 基础配置2.2 启动事件2.3 填写请假单2.4 上级领导审批3.5 经理审批3…...
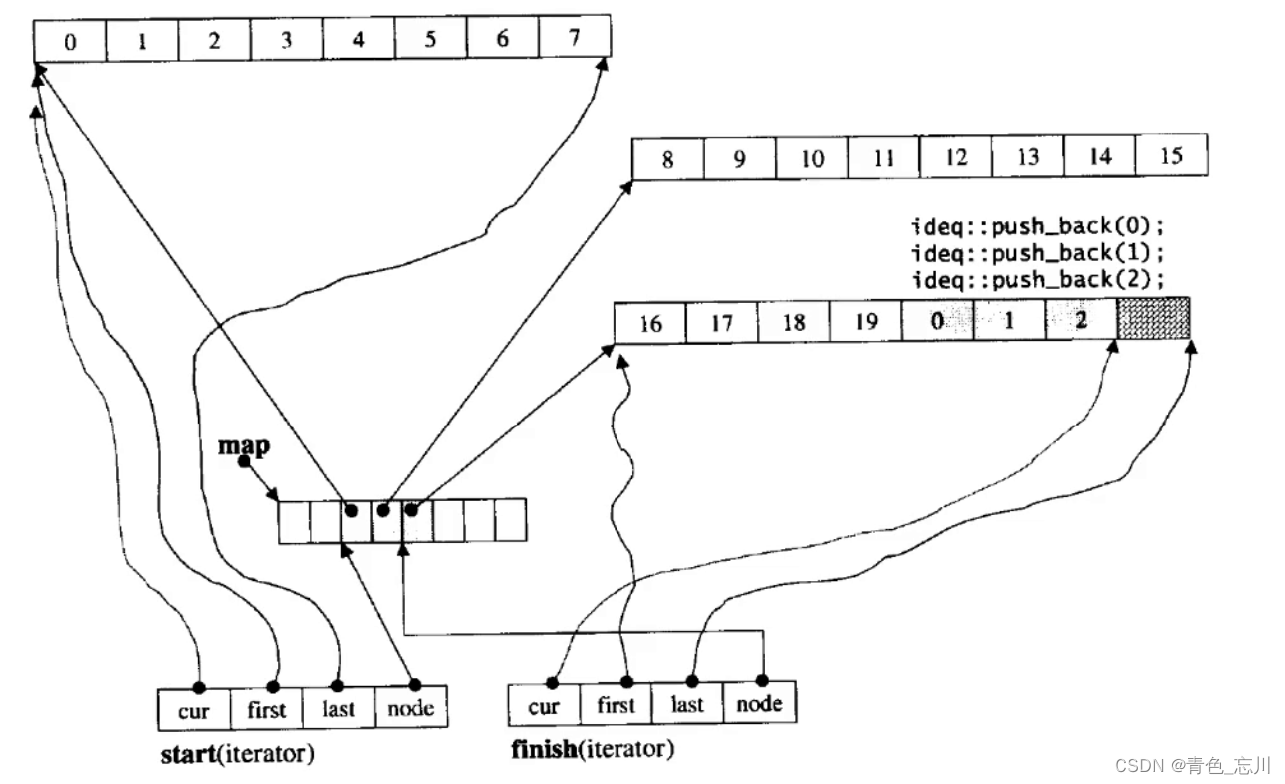
【C++从0到王者】第十七站:手把手教你写一个stack和queue及deque的底层原理
文章目录 一、stack1.利用适配器2.栈的实现 二、queue三、deque1.deque介绍2.deque的接口3.deque的基本使用4.deque的效率5.deque的原理 一、stack 1.利用适配器 我们不可能写了一份数组栈以后,还要在手写一个链式栈,这样显得太冗余了。于是我们可以利…...
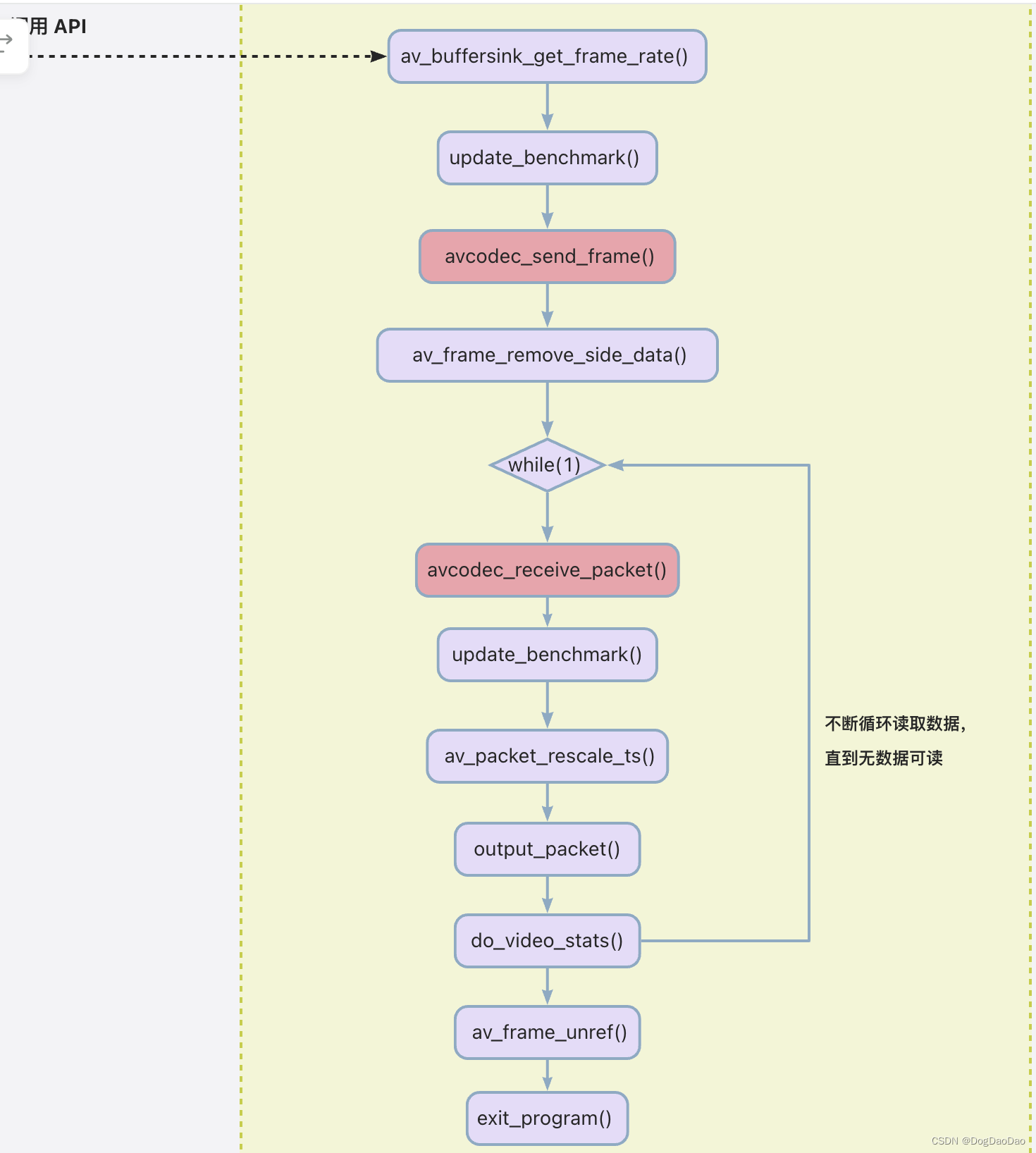
ffmpeg.c源码与函数关系分析
介绍 FFmpeg 是一个可以处理音视频的软件,功能非常强大,主要包括,编解码转换,封装格式转换,滤镜特效。FFmpeg支持各种网络协议,支持 RTMP ,RTSP,HLS 等高层协议的推拉流,…...

GD32F103待机模式与唤醒
GD32F103待机模式与唤醒,本程序使用RTC报警唤醒。 电源管理单元有3种省电模式:睡眠模式,深度睡眠模式和待机模式; 进入待机模式的步骤如下: 若需要RTC闹钟输出,则需要将TAMPER-RTC映射到PC13引脚; 若需要LXTAL晶振32.768KHz&…...
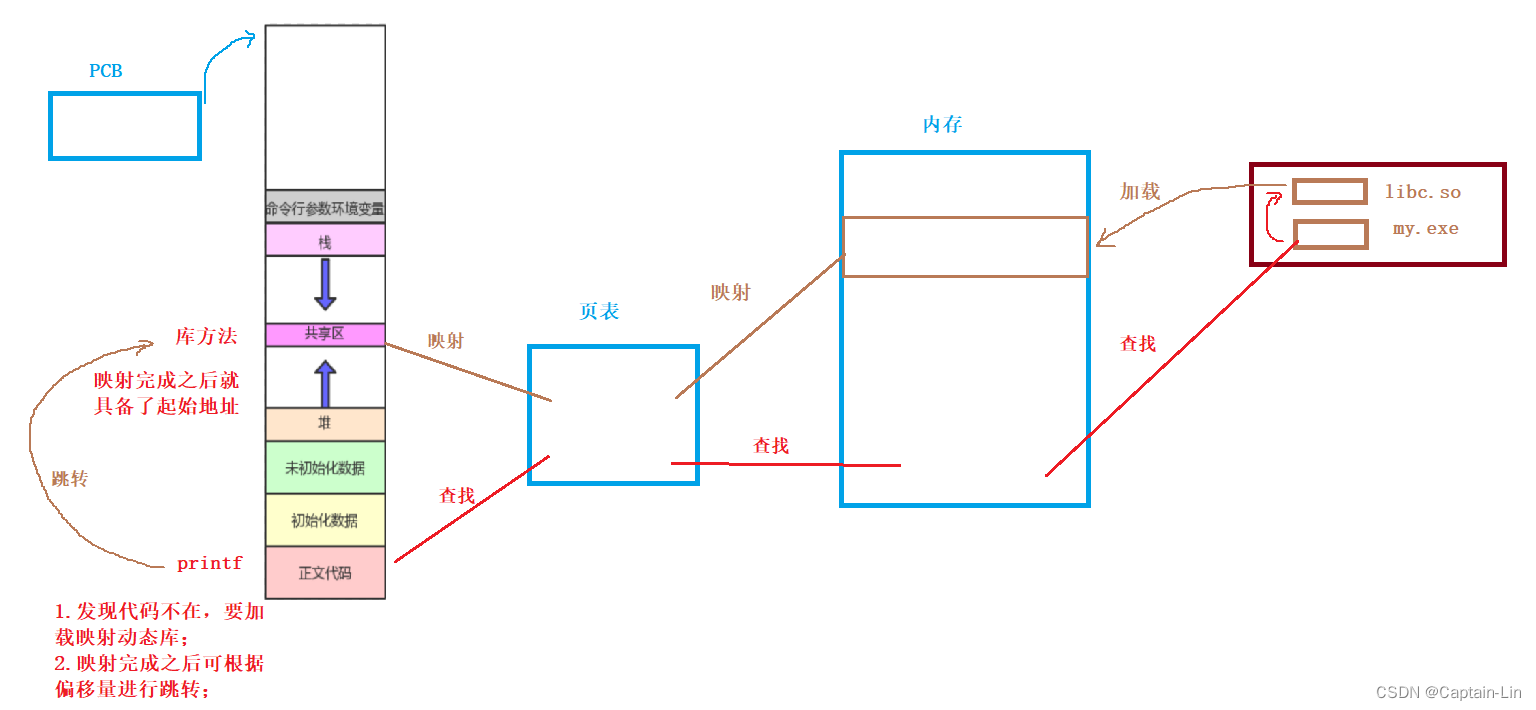
【Linux初阶】基础IO - 动静态库 | 初识、生成、链接、加载
🌟hello,各位读者大大们你们好呀🌟 🍭🍭系列专栏:【Linux初阶】 ✒️✒️本篇内容:动静态库初识,库的含义,静态库的生成与链接,gcc/g默认链接方式,…...

为Git仓库设置签名信息
前言 在首次使用git版本库或创建新的仓库时,需要为其仓库设定管理员和管理员邮箱。 在为仓库添加管理员和邮箱地址时,有以下两种情况: (1)全局模式:首次创建,后面做为默认使用,对当…...

iOS开发Swift开发UI页面链式调用库推荐
首页链接 https://github.com/zhiguangqiao/ChainableUIKit 安装方法 pod ChainableUIKit调用片段 UIButton import ChainableUIKitprivate let button UIButton().chain.setTitleColor(.init(hex: "#9583EB"), state: .normal).setTitle("全部视频",…...
ClickHouse SQL与引擎--基本使用(一)
1.查看所有的数据库 show databases; 2.创建库 CREATE DATABASE zabbix ENGINE Ordinary; ATTACH DATABASE ck_test ENGINE Ordinary;3.创建本地表 CREATE TABLE IF NOT EXISTS test01(id UInt64,name String,time UInt64,age UInt8,flag UInt8 ) ENGINE MergeTree PARTI…...

2023-08-07力扣今日七题-好题
链接: 剑指 Offer 11. 旋转数组的最小数字 154. 寻找旋转排序数组中的最小值 II 题意: 找一个数组里的最小值,这个数组是有非递减数组旋转而来的,旋转n次表示把前n个数移动到数组末尾 解: 很有趣的二分ÿ…...
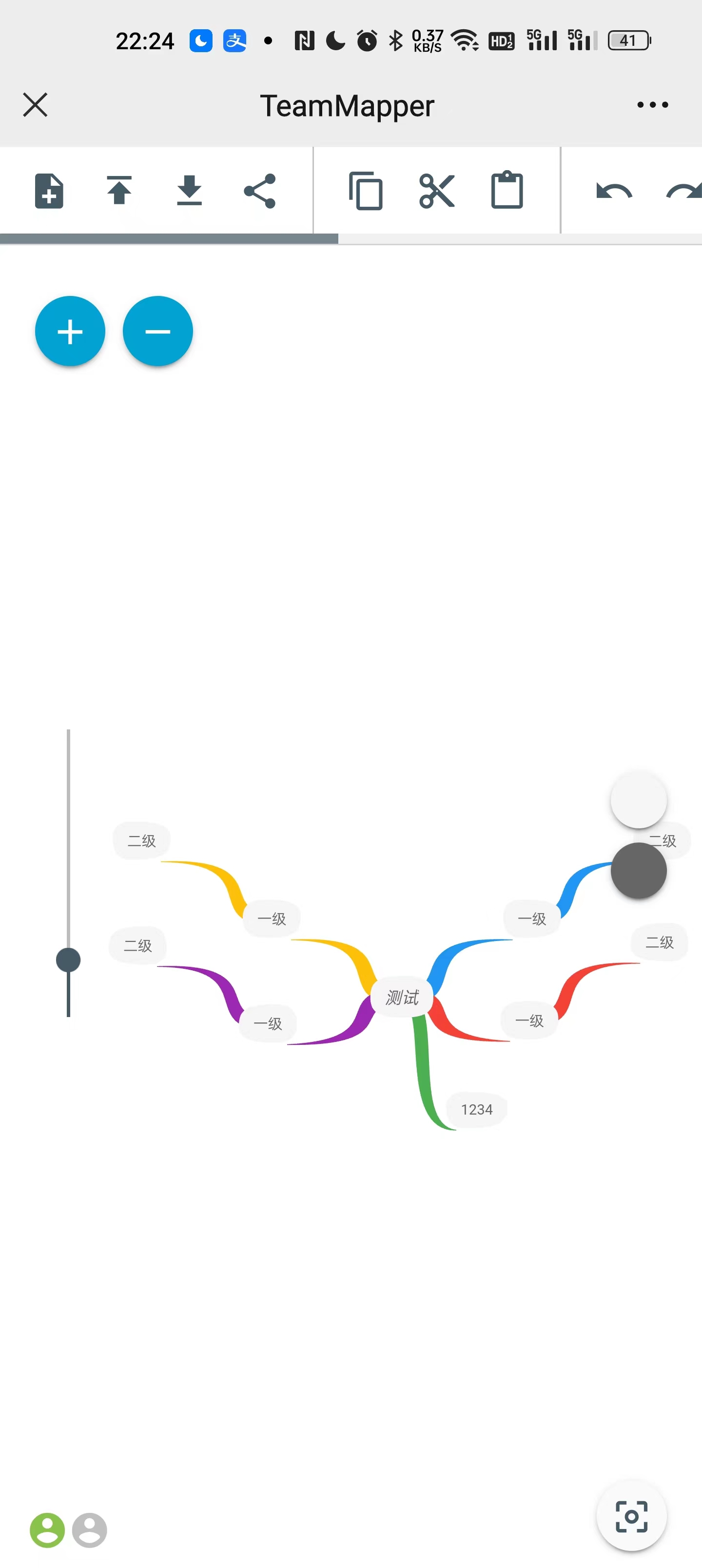
支持多用户协同的思维导图TeamMapper
什么是 TeamMapper ? TeamMapper 是基于 Mindmapp 开发的用于绘制思维导图的 Web 应用程序。它使得思维导图变得简单,你可以托管并创建您自己的思维导图。与您的团队分享您的思维导图会议并在思维导图上进行协作。 软件特点: 创建࿱…...

【Vue】Parsing error: No Babel config file detected for ... vue
报错 Parsing error: No Babel config file detected for E:\Study\Vue网站\实现防篡改的水印\demo02\src\App.vue. Either disable config file checking with requireConfigFile: false, or configure Babel so that it can find the config files. …...

2023-08-07力扣今日五题
链接: 剑指 Offer 53 - II. 0~n-1中缺失的数字 题意: 如题 解: 长度n的递增数组里,要找0到n中没出现的那个数字,那么出现的下标是0到n-1,一一对应即可,都出现了就是n没有 实际…...
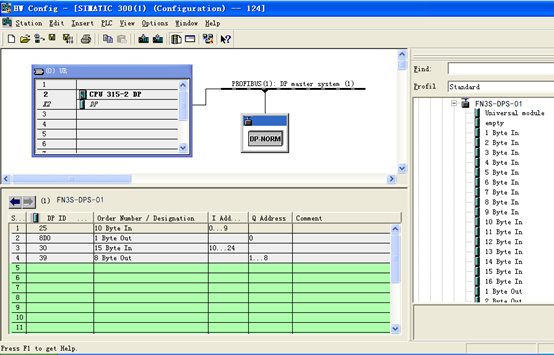
ETHERCAT转PROFIBUS连接到300plc的配置方法
由于捷米JM-DP-ECT,是自主研发的一款PROFIBUS从站功能的通讯网关,它的主要功能是将ETHERCAT设备接入到PROFIBUS网络中生产环境比较复杂有多个设备采用不同的协议这极大的阻碍了,各个设备的数据互通。 JM-DP-ECT这个小小的网关可不简单&#x…...
Spring Boot配置文件与日志文件
1. Spring Boot 配置文件 我们知道, 当我们创建一个Spring Boot项目之后, 就已经有了配置文件存在于目录结构中. 1. 配置文件作用 整个项目中所有重要的数据都是在配置文件中配置的,比如: 数据库的连接信息 (包含用户名和密码的设置) ;项目的启动端口;第三方系统的调…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...
