Leetcode-每日一题【剑指 Offer 07. 重建二叉树】
题目
输入某二叉树的前序遍历和中序遍历的结果,请构建该二叉树并返回其根节点。
假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
示例 1:
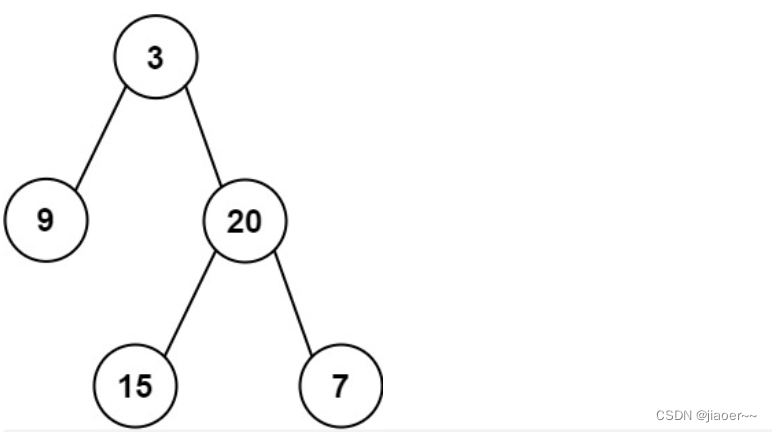
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]
示例 2:
Input: preorder = [-1], inorder = [-1]
Output: [-1]
限制:
- 0 <= 节点个数 <= 5000
解题思路
1.题目要求我们利用前序遍历和中序遍历构建出二叉树,我们可以画图来理解一下
举个例子:
根据我们对数据结构中二叉树部分的学习,我们知道前序遍历是(根左右)所以第一个元素一定是这颗二叉树的根。
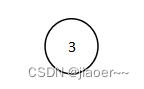
那么中序遍历是(左右根),所以数字 3 左边的是它的左子树部分,右边的是他的右子树部分。 设 3 在数组 inorder中的下标为 i,
前序遍历:左子树部分 [ l1 + 1, l1 + (i - l2) ] 右子树部分 [l2, i - 1]
中序遍历:左子树部分 [l1 + (i - l2) + 1, r1] 右子树部分[i + 1, r2]
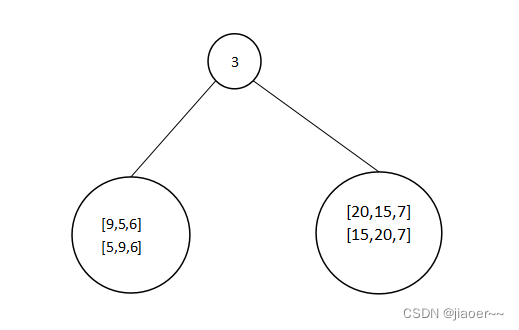
我们按照这个思想继续处理 3 的左子树和右子树, 也就是进行递归操作,
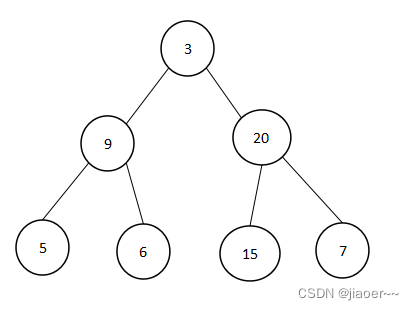
3 的左子树中 9 为根节点,那么 5 和 6 为 9 的左右子树,3 的右子树中 20 为根节点,15 和7 为 3 的左右子树。最终生成的数如下图所示
2.代码部分首先我们判断所给数组是否为空,若为空直接返回 null;然后我们新建一个map 用于存储inorder数组的下标和对应的值,方便我们后序对 root 所对应的数组下标进行查找。
然后我们让root = f( ) 函数。
3.f( ) 函数的作用是利用传入的前序遍历和中序遍历的数组,找到二叉树的 root 节点,并将数组划分为 root 节点的左右子树。结束条件为 r1 < l1 && r2 < l2。处理完成后返回 root 即可。
代码实现
class Solution {Map<Integer,Integer> map = new HashMap();public TreeNode buildTree(int[] preorder, int[] inorder) {if(preorder == null || preorder.length <= 0){return null;}for(int i = 0; i < inorder.length; i++){map.put(inorder[i],i);}TreeNode root = f(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1);return root;}public TreeNode f(int[] preorder, int l1, int r1, int[] inorder, int l2, int r2){if(r1 < l1 && r2 < l2){return null;}TreeNode root = new TreeNode(preorder[l1]);int i = map.get(preorder[l1]);root.left = f(preorder, l1 + 1, l1 + (i - l2), inorder, l2, i - 1);root.right = f(preorder,l1 + (i - l2) + 1, r1, inorder, i + 1, r2);return root;}
}测试结果

相关文章:

Leetcode-每日一题【剑指 Offer 07. 重建二叉树】
题目 输入某二叉树的前序遍历和中序遍历的结果,请构建该二叉树并返回其根节点。 假设输入的前序遍历和中序遍历的结果中都不含重复的数字。 示例 1: Input: preorder [3,9,20,15,7], inorder [9,3,15,20,7]Output: [3,9,20,null,null,15,7] 示例 2: Input: preo…...

Shell编程快速入门
Shell编程快速入门 脚本格式要求 脚本以#!/bin/bash开头脚本需要有可执行权限 脚本的常用执行方式 方式1:输入脚本的绝对路径或相对路径方式2:sh脚本 Shell的变量 Shell变量介绍 Linux Shell中的变量分为系统变量和用户自定义变量 系统变量&#…...

wpf 3d 坐标系和基本三角形复习
wpf 3d 坐标系的描述见此, WPF 3d坐标系和基本三角形_wpf 坐标系_bcbobo21cn的博客-CSDN博客 X轴正向向右,Y轴正向向上;Z轴,正向是从屏幕里边出来,负向是往屏幕里边去;坐标原点是在呈现区域的中心&#x…...

如何安全变更亚马逊收款账户?
有太多的卖家想知道如何安全变更亚马逊收款账户,因为更改了第三方收款账户可能会导致二次视频认证或者增强视频。真的是这样吗? 其实不推荐亚马逊店铺正常运营之后去变更信用卡,收款账户等重要资料的,因为玩黑科技的卖家也真的多…...

大数据面试题:Hadoop中的几个进程和作用
面试题来源: 《大数据面试题 V4.0》 大数据面试题V3.0,523道题,679页,46w字 可回答:1)启动Hadoop,都会有什么进程 参考答案: 1)NameNode:Master…...

题解:ABC276D - Divide by 2 or 3
题解:ABC276D - Divide by 2 or 3 题目 链接:Atcoder。 链接:洛谷。 难度 算法难度:入门。 思维难度:入门。 调码难度:入门。 综合评价:极简。 算法 数论。 思路 由大脑可知&#x…...

后台管理系统
1.1 项目概述 简易后台管理系统是一个基于Vue3ElemrntPlus的后台管理系统,提供了用户登录、记住密码、数据的增删改查、分页、错误信息提示等功能,旨在协助管理员对特定数据进行管理和操作。 没有后台对接,数据源为假数据。 全部代码已上传G…...

C++数据结构之平衡二叉搜索树(一)——AVL的实现(zig与zag/左右双旋/3+4重构)
本文目录 00.BBST——平衡二叉搜索树01.AVL树02.AVL的插入2.1单旋——zig 与 zag2.2插入节点后的单旋实例2.3手玩小样例2.4双旋实例2.5小结 03.AVL的删除3.1单旋删除3.2双旋删除3.3小结 04.34重构05.综合评价AVL5.1优点5.2缺点 06.代码注意插入算法删除算法完整代码:…...
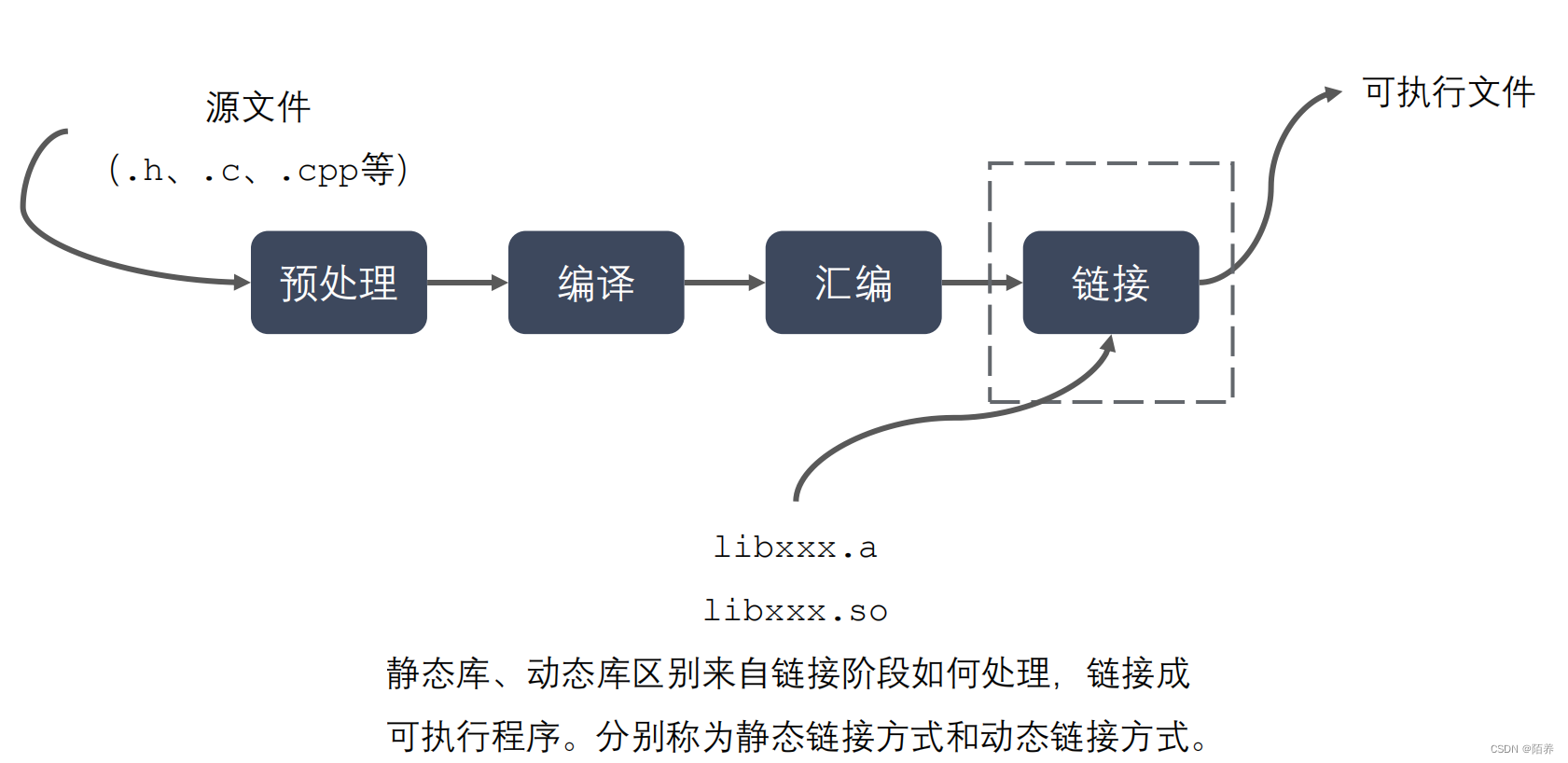
静态库和动态库
库文件 库文件是计算机上的一类文件,可以简单的把库文件看成一种代码仓库,它提供给使用者一些可以直接拿来用的变量、函数或类。 库是特殊的一种程序,编写库的程序和编写一般的程序区别不大,只是库不能单独运行。库文件有两种&a…...

用于Voronoi图构建的Fortune算法的C++实现
Voronoi图是一种在计算几何中广泛使用的数据结构,它可以用于解决最近邻搜索、路径规划等问题。在这篇文章中,我们将探讨一种用于构建Voronoi图的高效算法——Fortune算法,并提供其C实现。 一、Voronoi图简介 Voronoi图是由一组点在平面上生…...

笔记汇总 | 斯坦福 CS229 机器学习
文章目录 前言课程参考文章推荐阅读 前言 本文为斯坦福大学 CS229 机器学习课程学习笔记 本文主体部分转载自黄海广博士,文末已给出链接,大家有兴趣可以直接访问笔记首页,下载对应课程资料及作业代码 课程官网:CS229: Machine …...

git 版本管理工具 学习笔记
git 学习笔记 目录 一、git是什么 二、创建仓库 三、工作区域和文件状态 四、添加和提交文件 五、回退版本 (了解) 六、查看差异 七、删除文件 八、.gitignore文件(了解) 九、github ssh-key配置 十、本地仓库和远程仓库内…...
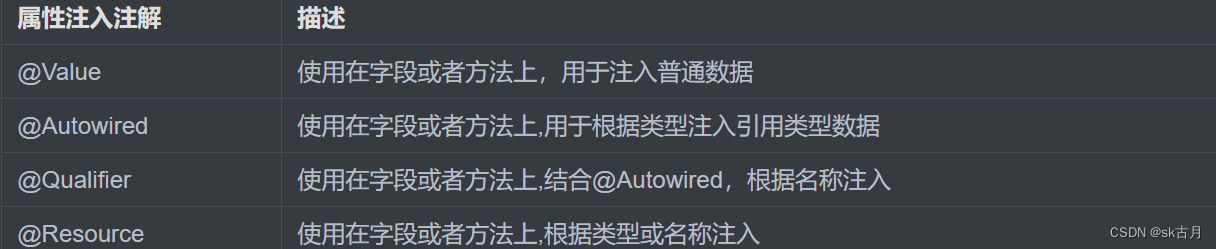
Bean基本注解开发和Bean依赖注入注解开发
目录 1.Bean基本注解开发 Component Scorelazy PostConstruct和PreDestroy RepositoryServiceController 2.Bean依赖注入注解开发 Value Autowired Qualifier Resource 扩展AutoWired 1.Bean基本注解开发 基本Bean注解,主要是使用注释的方式替代原有xml的…...
使用IIS服务器搭建一个网站
参考文章 使用IIS(Internet Information Services)服务器搭建一个网站相对来说是比较简单的。以下是基本的步骤: 安装IIS: 首先,确保你的操作系统已经安装了IIS。在大多数Windows版本中,IIS都是可选安装项…...
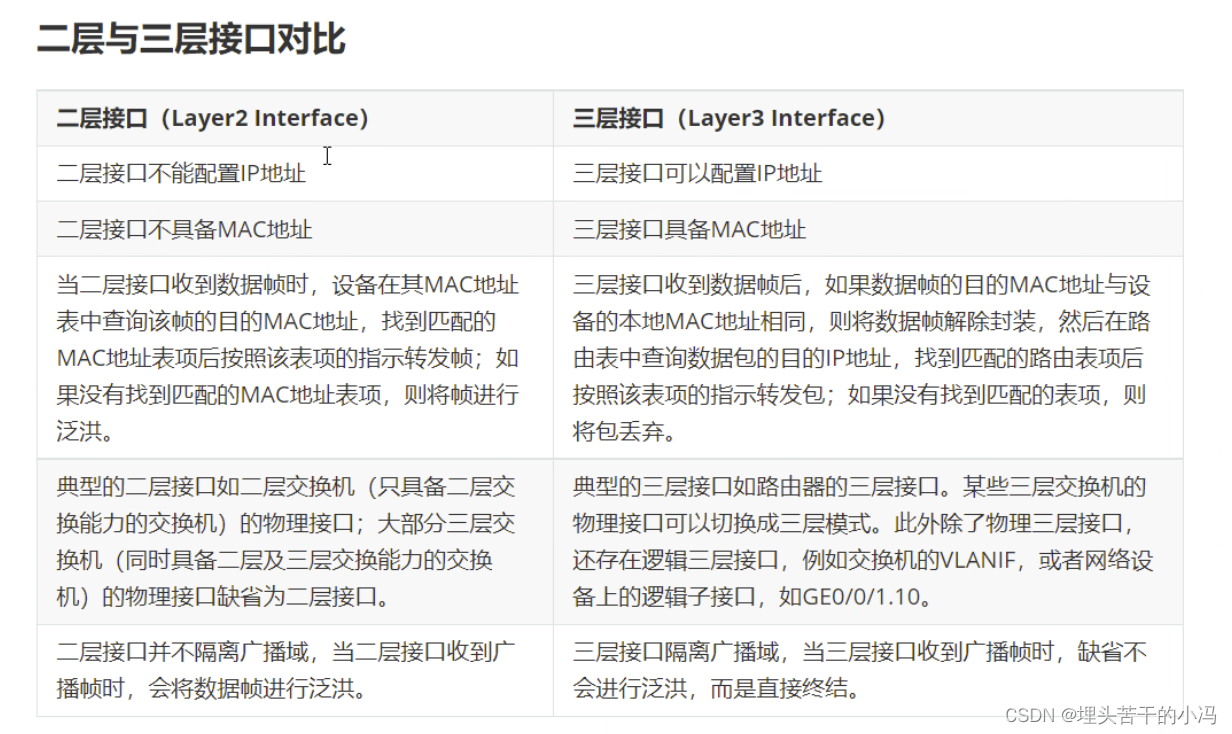
HCIP 三层交换机
一、实现VLAN间通信 在传统的交换机组网中,默认所有网络都处于同一个广播域,带来了许多问题,VLAN技术的提出,满足了二层组网隔离广播域需求,使得属于不同的VLAN间网络无法通信,但不同VLAN之间又存在着互相…...
第二章小结)
利用python 进行数据分析(第三版)第二章小结
利用python 进行数据分析(第三版)第二章小结 由于是闲暇时间看的,且为读书笔记,所以只会写一些心得和容易混淆的知识,简单知识将不在重复 在变量或者函数后使用?可以查看详细信息。?还有最后一个用途,即…...

【ASP.NET MVC】使用动软(四)(12)
一、筛选器类和Cookie实现路由 需解决的问题: 网站登录往往需要用户名密码验证,为避免重复验证,一般采用Cookie 、Session等技术来保持用户的登录状态: Session是在服务端保存的一个数据结构,用来跟踪用户的状态&…...
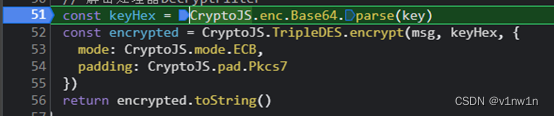
【web逆向】全报文加密及其登录流程的分析案例
aHR0cHM6Ly9oZWFsdGguZWxkZXIuY2NiLmNvbS9zaWduX2luLw 涉及加密库jsencrypt 定位加密点 先看加密的请求和响应: 全局搜索加密字段jsondata,这种非特定参数的一般一搜一个准,搜到就是断点。起初下的断点没停住,转而从调用栈单步…...

MyBatis枚举映射类讨论
前言 本篇需要对于MyBatis有一定的认识,而且只是针对于TypeHandler接口来讨论,暂不讨论其他方面的问题 TypeHandler概叙 TypeHandler是MyBatis设计的一个用于参数的接口,你们会不会很好奇MyBatis是如何把整形,时间,字符…...
微信开发之朋友圈自动点赞的技术实现
简要描述: 朋友圈点赞 请求URL: http://域名地址/snsPraise 请求方式: POST 请求头Headers: Content-Type:application/jsonAuthorization:login接口返回 参数: 参数名必选类型说明wId…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...